天然气掺氢在管道流动中的氢浓度分布1)

安永伟 孙 晨 冀守虎 贾冠伟 许未晴 ,,2) 刘 伟 ,3) 周 亮 蔡茂林 ,

*(河南大学物理与电子学院，河南开封 475004)

†(国家电投集团科学技术研究院有限公司，北京 102209)

**(北京航空航天大学自动化科学与电气工程学院，北京 100191)

††(气动热力储能与供能北京市重点实验室，北京 100191)

***(正星氢电科技郑州有限公司，郑州 450000)

全球化石能源消耗占比高达83%[1]，导致严重的生态环境危机，影响人类生存。氢能是全球能源走向低碳化、清洁化，发展潜力最大的非化石能源之一。全球氢能预计在2050年能源消耗占比增长至18%[2]。许多国家积极探讨氢能发展政策，并发布了国家的氢能发展战略。我国化石能源消耗占比为74.5%[3]。依据构建能源体系发展需求，国家发展改革委、国家能源局联合发布了《氢能产业发展中长期规划(2021—2035年)》等氢能发展政策保障促进发展氢能产业，实现氢能的高效利用[4]，确保完成“双碳”任务。

利用可再生能源（水电、风电、光电等）制氢是解决传统制氢领域高碳排放的有效途径。目前，我国可再生能源占全球可再生能源发电量的24.4%，位于首位[5]；同时，我国的电解水制氢的成本为2.6美元/kg，远低于日本的4.6美元/kg，成本优势和规模巨大。由于我国可再生能源主要集中于中西部地区，但电力和氢气的使用主要集中于东南沿海地区，导致了氢气生产、存储、输送及使用的不平衡和应用困难[6]。拖车运氢是一种主要的输气方式，但超过150 km，其输送成本增高，不适合大规模输送。现役天然气管网是解决当前氢气大规模、长距离输送的可行方式，也是氢气输送方式的研究热点[7]。我国在役天然气管道长度高达1.1×105km[8]，为氢气的输送提供设备基础并且输送成本也会逐渐降低[9]。然而，由于氢气扩散性较高，氢气在天然气管道中泄露速度是天然气泄露速度的3倍，且泄露速度受多种因素影响也会增加[10-11]，管线钢易腐蚀发生氢脆进而泄露[12]。目前鉴于天然气掺氢多集中于掺混热值的研究，对天然气掺氢比例及氢浓度分布的研究不多，因此，对国内天然气掺氢现状进行总结归纳。张立业等[13]综述了天然气掺氢随动掺氢系统类型及气体传感器对气体种类、浓度的测量，并通过国家电投朝阳天然气掺氢示范项目，实现了精准8.8%随动掺氢比例。

氢气和天然气密度差异可能引起流动分层，使氢气在管道中浓度分布不均，在局部形成氢气的聚集，影响掺氢管道输送的安全性，引起国内外研究者的关注。许未晴等[14]对管道掺氢中氢脆现象进行详细研究，介绍了氢脆现象发生的机理，对影响管道氢脆的因素总结，重点探讨了掺氢输送系统中管道、阀门、储存装置等部件的氢脆现象。Kong等[15]使用内置旋流器的螺旋静态混合器以减小流动的分层，对掺混气体甲烷和氢气混合过程进行了数值仿真，并采用空气和氦气模拟甲烷和氢气进行实验验证。不过，该混合器有着结构复杂、流阻大等缺陷，限制了实际应用。吴嫦[16]实验验证了直立管中天然气与氢气混合且静置后无分层现象，但未揭示其机理。Tabkhi等[17]提出了一种天然气管网数学建模框架，研究不同掺氢比传输能量的变化，发现并确定最大掺氢比为6%。Guandalini等[18]建立模型模拟管路中气体的传输，发现掺氢会导致流体密度和速度发生变化，使得传输能量降低，掺氢比为5%时管网压力下降0.1%。Hafsi等[19]提出了天然气网注氢效应的数学模型，探究注氢对天然气流动的影响，发现注入氢气会使管道内压降值升高，气体流速上升。Wiitkowski等[20]通过改变掺氢比例，探究氢气在两种管路中的最大安全输送距离，在内径0.15 m长度1.0×104m和内径1 m长度1.0×105m的管路中，最大安全输送距离分别为15 320 m和130 146 m。以上文献对掺氢比进行了研究，但对掺氢后气体流动过程中天然气和氢气浓度分布没有详细的分析。

鉴于天然气掺氢多集中于掺混热值和掺混比例的研究，但在役天然气管网结构复杂，掺氢后流动特性复杂。对于天然气掺氢后混气均匀性，天然气管路中氢气低速区和氢气聚集区研究较少。相关特性对于精准监测掺氢天然气浓度，为随动掺氢控制提供准确的反馈数据有着重要意义。此外，管路中氢气聚集区域易出现氢脆现象，严重影响氢气运输安全及管道寿命。因此，本文针对天然气掺氢后的掺混效果开展模拟研究，其结果具有一定应用指导意义。

1 掺混管路模型建立

为研究天然气管道掺氢过程中的掺混情况，采用国家电投朝阳天然气掺氢示范项目管网的尺寸和气体参数[13]。天然气进口管径为80 mm，流量为130.98 m3/h，氢气进口管径为25 mm，流量为14.55 m3/h。构建了T型掺混管路模型和变径掺混管路模型，通过这两种模型及9个变径模型对天然气和氢气浓度进行对比研究。T型掺混管路模型和变径掺混管路模型分别如图1和图2所示。

图1 掺混管路基本模型Fig.1 Basic model of blending pipeline

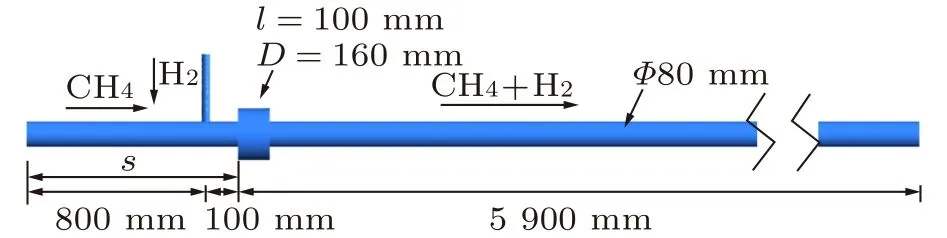
图2 掺混管路变径模型Fig.2 Variable diameter model of blending pipeline

1.1 T型掺混管路模型

T型掺混管路模型如图1所示，具体参数如下：天然气主管路内径为φ80 mm，掺混中心距出口长度为6 000 mm，氢气掺混管路位于主管路上方，垂直于主管路，管路内径为φ25 mm，长度为250 mm，中心距离主管路入口为800 mm。

1.2 变径掺混管路模型

变径掺混管路模型如图2所示，即在T型掺混管路模型中，增加一段与主管内径不同的直管，通过流动截面的突扩与突缩，强化掺混效果。具体参数如下：天然气主管路内径为φ80 mm，氢气掺混管路位于主管路上方，垂直于主管路，氢气管路内径为φ25 mm，长度为250 mm，中心距出口长度为6 000 mm。图2中参数对应变径掺混管路模型的基准参数，即变径开始位置s= 900 mm，内径D= 160 mm，长度l= 100 mm，相应参数的影响将在下文详细介绍。

2 数学模型

天然气和氢气在掺混过程中及在管道流动中的连续性方程

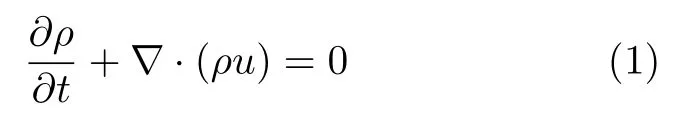
其中，ρ为气体的密度，u为气体的流速，t为流动时间。

掺混过程中及在管道流动中的动量方程

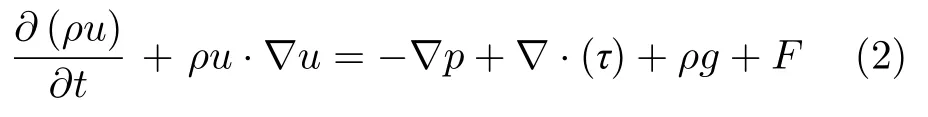
其中，p为静压，g为重力加速度，F为除重力外的外部体积力，τ为黏性剪切应力张量。鉴于掺混流动总是处于湍流状态，本文采用标准k–ε湍流模型模拟湍流输运特性。

掺混过程中及在管道流动中的能量方程为

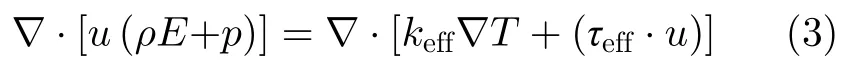
其中，E为能量，T为温度，keff为有效传热系数，τeff为有效黏性剪切应力张量。

天然气和氢气在掺混过程中及在管道流动中相互扩散，通过对第i种气体对流扩散方程的求解来预测每个气体的局部质量分数Yi。该守恒方程的一般形式为

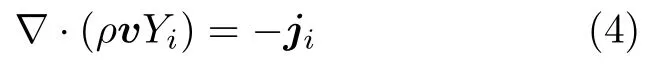
在气体掺混过程中，由浓度和温度梯度引起的第i种气体的扩散通量表达式为

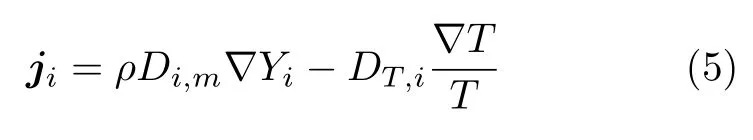
其中，Di,m为在混合气体中第i种气体组分的质量扩散系数，DT,i为热扩散系数。

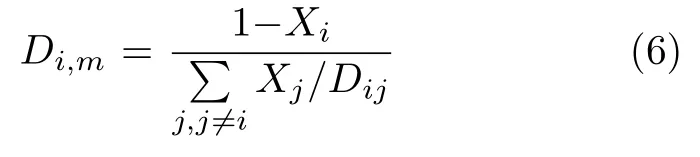
其中，Xi为第i种气体的摩尔分数，Dij为气体混合物的温度常数或多项式函数。

由于天然气掺氢的过程中，天然气和氢气遵循理想气体状态方程，由于压力、流量的变化，其掺混气体的浓度或密度会产生变化，具体的表达式为

其中，pop为掺混气体的工作压力，p为相对于pop的局部相对压力，R为气体常数，Mw为气体的分子量，T为气体的温度。

3 管路模型网格划分

仿真模拟天然气和氢气掺混并在管道中流动时，Fluent的计算精度取决于网格的密度。通常情况下，网格密度越大，仿真结果精度就高，但同时要使用更多计算资源和更长的计算时间。采用网格无关验证即可以保证计算结果的精度，又可以节省计算资源和时间。因此，本文网格划分采用低、适中、高密度三种形式来进行网格无关验证，如表1所示。以适中的网格特征为参考，通过T型和变径混管路模型的低密度网格和高密度网格计算，得出出口氢气摩尔分数的波动量分别为–2.6%～4.9%和0.6%。通过计算波动量可以排除网格密度对仿真结果的精度影响；同时，网格无关也得到了验证。

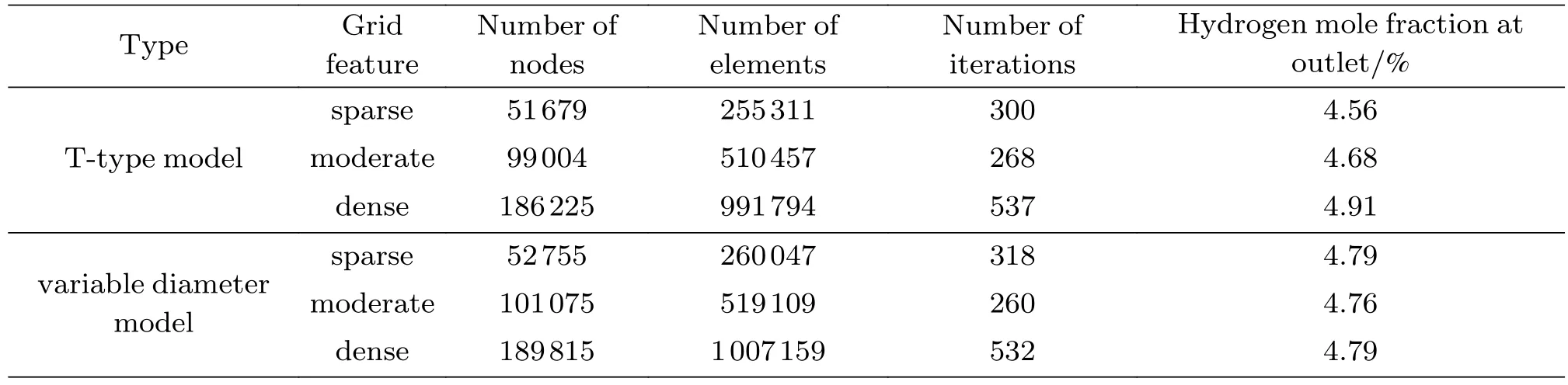
表1 网格无关性说明Table 1 Grid independence specification

因此，T型和变径掺混管路模型均以四面体结构进行网格划分，整体网格设置为8 mm，以便更清楚计算出流体运动状态。T型掺混管路模型的节点数为99 004个，单元数为510 457个，如图3所示；变径掺混管路模型节点数为101 075个，单元数为519 109个，如图4所示。

图3 T型掺混模型网格Fig.3 Grid of T-type blending model

图4 变径模型网格Fig.4 Grid of variable diameter model

4 边界条件设置

在Fluent中进行边界条件设置及仿真计算，将环境温度设为298 K，两个入口均为速度型入口，主管路入口速度为7.24 m/s（流量：131.0 m3/h），掺混管路入口速度为8.23 m/s（流量：14.6 m3/h），出口设置为自由流出。重力沿y轴负方向为9.8 m/s2，将稳态改为瞬态仿真，壁面函数设置为标准壁面函数，主管路入口气体为纯天然气，掺混管路入口气体为纯氢气。初始化选择混合初始化，将初始内部工质设为100%天然气。

5 模型求解

5.1 T型掺混管路流场分析

对于T型掺混管路数值仿真结果，T型掺混管路横截面速度和掺混处局部速度分布如图5所示。从图5可以看出，由于天然气和氢气的速度大小、方向均不相同，在掺混处发生掺混，两股气体交汇处，出现一个速度10 m/s左右的区域，即局部放大图的红色区域。在红色区域右侧靠近壁面位置，出现一个速度低于2 m/s的区域，即局部放大图的蓝色聚集区域，此后出现一段低速区，最初低速区占据了1/4管径高度，速度为6 m/s，随着掺混的进行，低速区占比沿着主管路逐渐减少，并在距掺混中心600 mm处消失。此后主管路中心速度在9 m/s左右，由于管壁的阻力作用越靠近管壁速度越低。

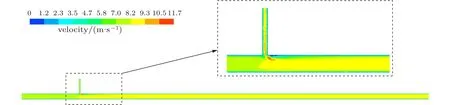
图5 气体掺混后速度云图Fig.5 Velocity distribution after gas blending

为更清晰观察到天然气掺氢的掺混效果，建立T型掺混管路横截面，气体掺混后天然气组分摩尔分数云图，如图6所示，气体掺混后氢气组分摩尔分数云图，如图7所示。相比天然气气体，由于掺混气体氢气具有更轻的质量，支管和主管路的速度大小和方向均不一样。因此在T型掺混管路中，氢气主要分布在主管路上半部分。在距掺混中心2 800 mm范围内出现明显分层，宽度占据1/3管径左右，随着掺混距离的增加，氢气摩尔分数和浓度逐渐降低，分层现象依然存在，但是氢气所占管径宽度逐渐减少。

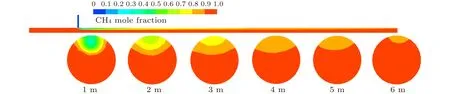
图6 气体掺混后天然气组分摩尔分数云图Fig.6 Mole fraction distribution of natural gas component after gas blending

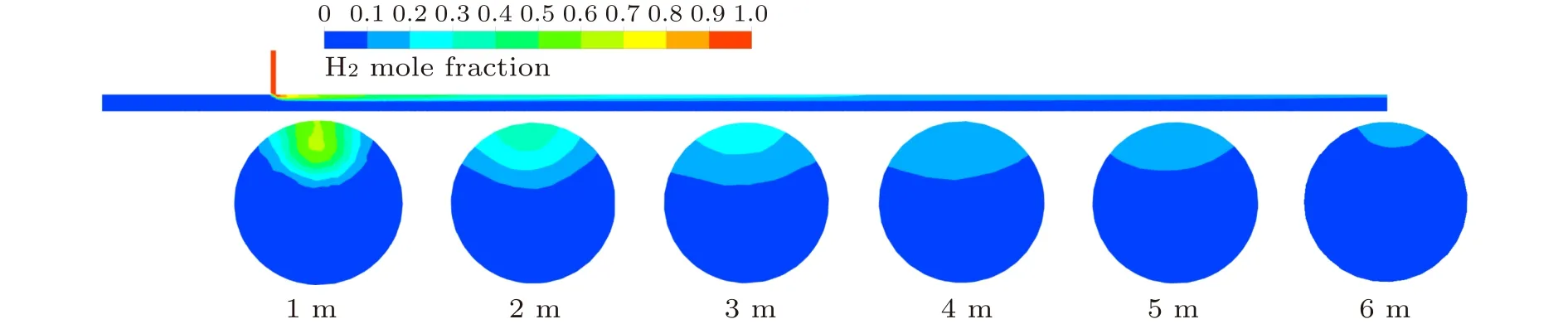
图7 气体掺混后氢气组分摩尔分数云图Fig.7 Mole fraction distribution of hydrogen component after gas blending

为探究掺混流动过程中的氢气浓度分布状态，选用T型掺混管路剖面图来表述掺混过程，分别选择了距主管路入口1 m，2 m，3 m，4 m，5 m，6 m处天然气和氢气的摩尔分数云图，如图6和图7所示。由于氢气密度低，主要分布于主管路中上部，随着掺混距离的增加，两种气体交汇处发生混合，氢气分布区域发生外扩，浓度进一步降低。随着距离的增加，管路中上部氢气摩尔分数逐渐降低，在主管路出口处，中上部氢气摩尔分数在20%以下。

掺混后，截面平均的天然气和氢气摩尔分数随掺混距离的变化如图8和图9所示，L表示距掺混中心的距离，x(CH4)表示甲烷摩尔分数，x(H2)表示氢气摩尔分数。从距离掺混中心处0.1 ～2.2 m，天然气的摩尔分数由最初的90.1%逐渐升高到93%，随着掺混距离的增加呈上升趋势；氢气的摩尔分数由最初的9.9%降至7%，随着掺混距离的增加呈下降趋势。不过，随着距离的增加，无论是天然气还是氢气，其摩尔分数的变化趋势均明显变缓，掺混管路出口氢气占比为4.7%。

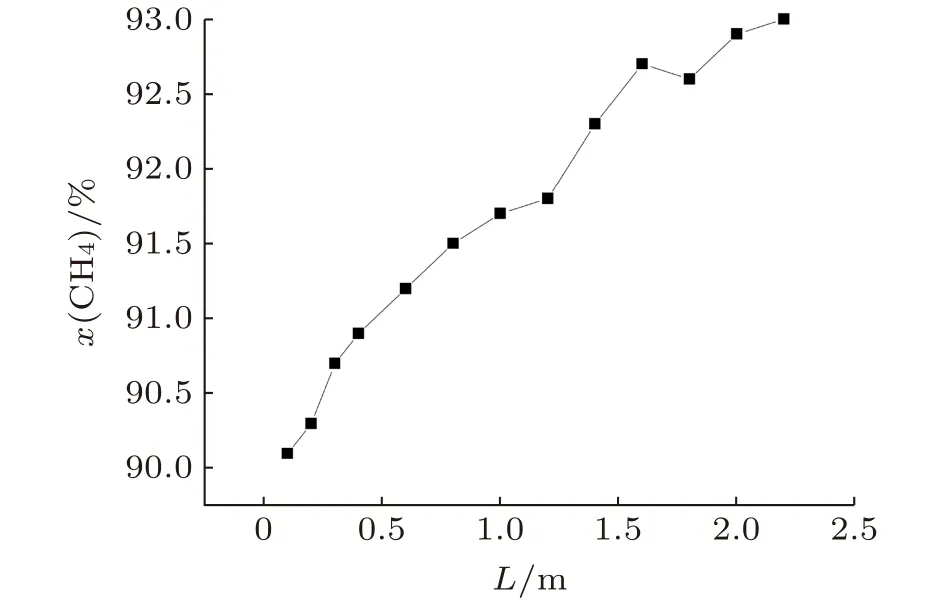
图8 T型管路掺混后天然气摩尔分数Fig.8 Percentage distribution of natural gas component with T-type pipeline after gas blending

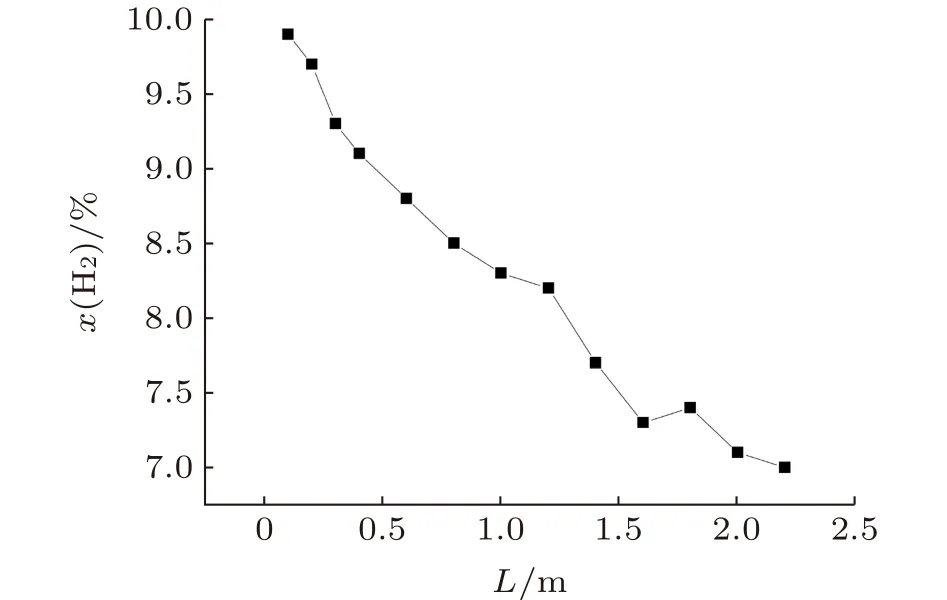
图9 T型管路掺混后氢气摩尔分数Fig.9 Percentage distribution of hydrogen component with T-type pipeline after gas blending

5.2 变径掺混管路流场分析

为探究在变径掺混管路中最容易发生氢气富集及其易引发氢脆的位置，构建了10种变径管路，如表2所示，通过改变变径模型的几何参数进行仿真，其中s表示变径距主管路入口的距离，D表示变径的直径，l表示变径的长度，x(H2)表示变径处氢气摩尔分数。根据4.1节中T型掺混管路流场分析，因为氢气低密度，所以在流动过程中会漂浮在主管路上半部分，因此变径处氢气摩尔分数只考虑变径上半部分。

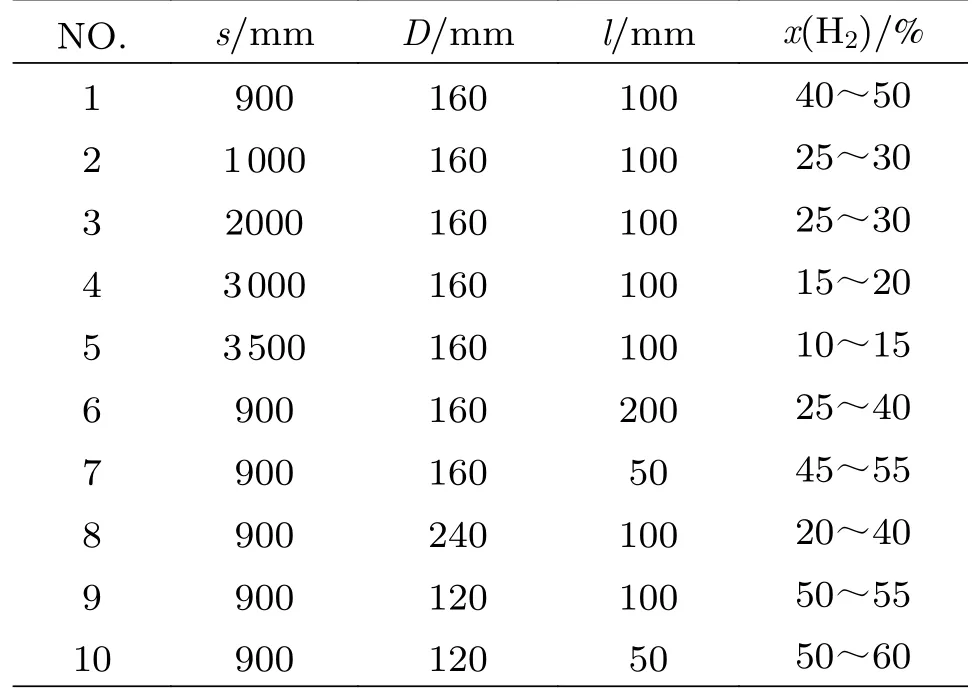
表2 变径掺混管路几何参数及结果Table 2 Geometric parameters and results of variable diameter type blending pipeline

以1号变径管路作为基准，固定变径直径、长度，不断改变变径位置，得到2～5号变径管路。对比前五个变径管路，发现变径处氢气摩尔组分最高的是初始模型，氢气摩尔分数达到40%～50%，2～5号变径管路氢气摩尔分数随着变径位置的增加不断降低，在10%～30%范围内。结果表明距离掺混中心越近，氢气和天然气混合的时间越短，变径处氢气摩尔分数越高。确定最优变径位置后，以1号变径管路作为初始管路，固定变径位置，将变径长度变宽、变窄，将变径直径变高、变低，得到6～9号变径管路，分析四种变径管路输出结果，发现变径长度变窄、直径变低时变径处氢气摩尔分数显著升高。结合上述分析结果，以1号变径管路作为初始管路，固定变径位置，将变径长度变窄，直径变低，得到10号变径管路，仿真结果显示变径处氢气摩尔分数达到50%～60%，在10个变径管路中占比最高，符合探究规律。下面对10号变径管路开展进一步具体研究。

以1号变径管路作为基准，固定变径位置，将变径长度变窄，直径变低，得到10号变径管路，对于变低变窄变径管路数值仿真结果，沿管长截面速度分布以及掺混处和变径处局部速度分布如图10所示。由于变径管路是在掺混管路上的延伸，仅仅对掺混处右侧管路进行修改，并未修改气体的速度、工质、方向等条件，因此变径管路掺混处的速度分布与4.1节掺混管路分析结果一致，同样出现红色、蓝色聚集区域。由于变径的存在，大量氢气注入上变径中，低速区大大减少，由原来的600 mm缩短至150 mm。变径处中心速度在8 m/s左右，越往外速度越低，易发生氢气聚集。截面较好地表示了变径边缘处的速度，整体速度在1 m/s以下，圆环左壁面的速度较低，接近于0 m/s，可认为是静止点，越往右速度越高。两种气体经过变径后，在管路中心形成一个高速区，速度在9 m/s以上，持续了1 100 mm后消失，之后速度保持在8～9 m/s范围内。

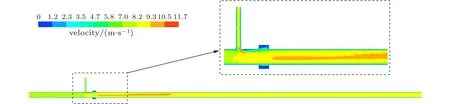
图10 气体掺混后速度云图Fig.10 Velocity distribution after gas blending

为更清晰地观察到掺混结果，建立变径掺混管路横截面，掺混后天然气组分摩尔分数云图如图11所示，氢气组分摩尔分数云图如图12所示。在距掺混中心1 600 mm范围内出现明显分层，宽度为1/3管径，随着掺混距离的增加，氢气摩尔分数逐渐降低，占管径宽度逐渐减少。由于氢气密度低，主要分布在管路上半部分，因此只考虑上变径摩尔分数。在上变径处氢气摩尔分数在50%～60%左右。

为探究变径内部氢气分布状态，选用变径处剖面图来表述掺混效果，分别选择了变径入口，中间、出口剖面图，如图11和图12所示。从变径入口至变径出口，由于天然气和氢气的混合，变径左壁面中上处的黄色区域被逐渐稀释，氢气摩尔分数不断降低。但是变径上方处的氢气摩尔分数变化不大，始终维持在50%～60%。根据速度分布图10所示，变径处速度从左到右逐渐增加，因此最容易发生氢气富集区域是变径左壁面正上方，该区域不仅具有较高的氢气浓度，而且速度也较低，接近静止，进而引发管道的氢脆。

掺混后，天然气和氢气的摩尔分数随掺混距离的变化如图13和图14所示，L表示距掺混中心的距离，x(CH4)表示甲烷摩尔分数，x(H2)表示氢气摩尔分数。距掺混中心0.09～0.1 m和0.149～0.15 m摩尔分数变化较大，分别是进入变径、离开变径所致。相比管路，变径内部氢气浓度较高，因此出现较大变化。如果将管路和变径分为两个部分进行分析，单独看变径或管路规律是一致的。从距离掺混处中心0.05～2.2 m，天然气的摩尔分数由最初的87.8%逐渐升高到93.1%，呈上升趋势。氢气的摩尔分数由最初的12.2%逐渐降至6.9%，氢气摩尔分数呈下降趋势。主管路出口处天然气、氢气云图如图11和图12所示，变径掺混管路模型出口处氢气的摩尔分数为4.8%。

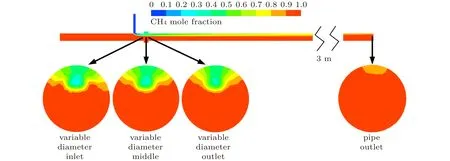
图11 气体掺混后天然气组分摩尔分数云图Fig.11 Mole fraction distribution of natural gas component after gas blending

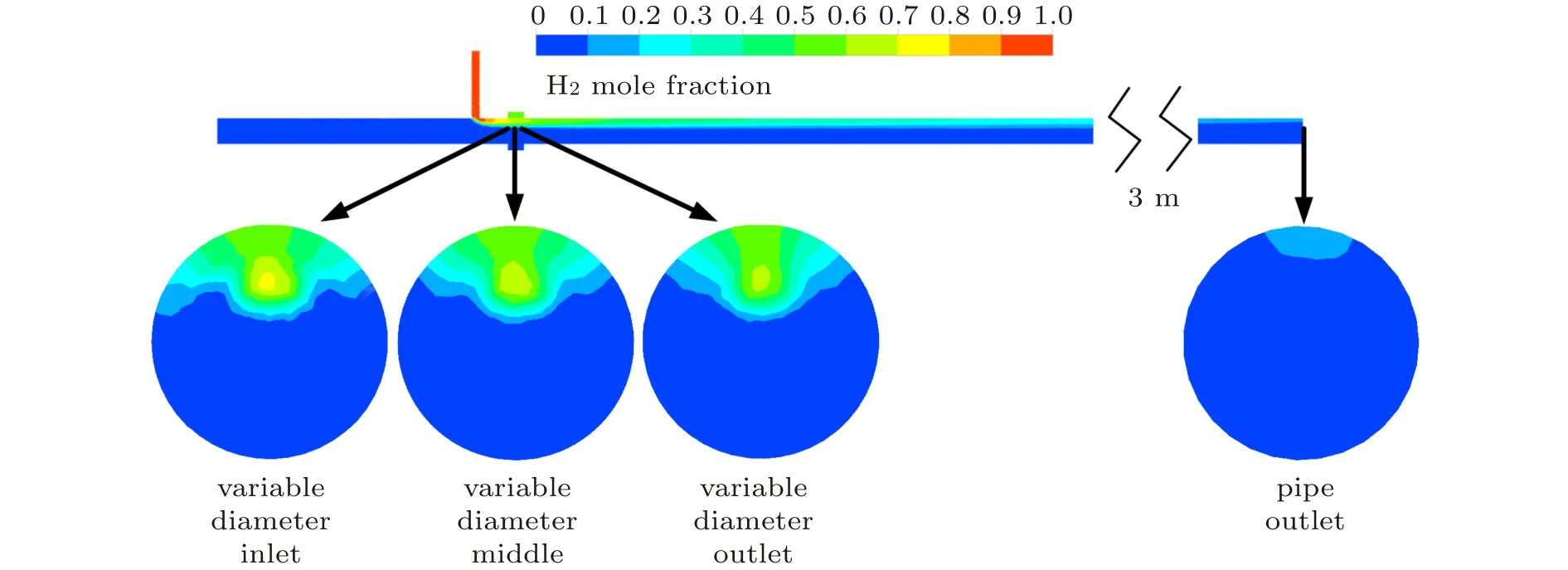
图12 气体掺混后氢气组分摩尔分数云图Fig.12 Mole fraction distribution of hydrogen component after gas blending

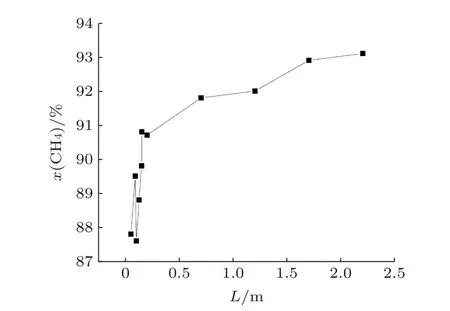
图13 掺混后天然气摩尔分数Fig.13 Percentage distribution of natural gas component after gas blending

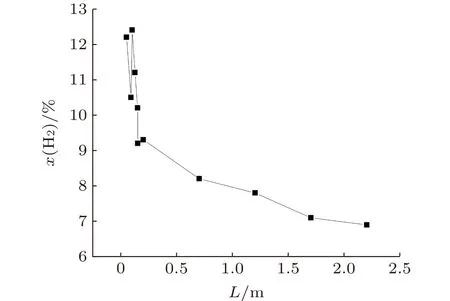
图14 掺混后氢气摩尔分数Fig.14 Percentage distribution of hydrogen component after gas blending

6 结论

为研究天然气掺氢过程中在管道中的掺混效果和氢气浓度的分布状况，通过构建T型和变径掺混管路模型，基于Fluent对T型掺混管路和10种变径掺混管路进行数值模拟研究，重点研究了管路中氢气组分、速度、聚集的规律，得出如下结论。

（1）对于T型掺混管路，气体交汇处拐角存在速度为0的蓝色区域。相比天然气，氢气密度低、质量轻，掺混过程中氢气主要分布在管路上方，在距掺混中心2 800 mm范围内出现明显分层，即在管长是管径35倍处内依然有一定分层，宽度占据1/3管径左右。

（2）对于变径管路，变径段内部速度较低，尤其是左壁面速度接近0，易引起氢气富集进而引起管道氢脆；窄细变径模型容易发生氢气聚集，氢气摩尔分数达到50%～60%。

本文结果表明，氢气和天然气密度差导致流动分层，存在混合不均匀的问题；通过混合器结构优化可以提高掺混均匀性。相关结果可对天然气掺氢掺混效果和管道变径选取提供参考，也为掺氢天然气掺混浓度测量点位设置提供指导，对发展随动掺混技术具有指导意义。