流化床生物质燃烧过程中传热特性的CFD–DEM数值模拟1)

谢 俊 牛淼淼 **

*(南京师范大学能源与机械工程学院，南京 210046)

†(东南大学能源与环境学院，南京 210096)

**(南京工程学院能源与动力工程学院，南京 211167)

温室气体减排和碳中和已经成为全球关注的热点议题，作为产生CO2的源头，以煤为代表化石能源的消耗量受到越来越多的限制，世界各国都已经将提高可再生能源在能源系统中的占比作为能源发展的重要目标。生物质能由于储量丰富、清洁低碳、应用广泛等特点受到了国内外学者和工业界的大量关注[1]。在诸多反应装置中，流化床锅炉有着燃料适应性广、燃烧效率高、污染物排放低等优势，尤其适用于生物质热化学转化过程。虽然直燃发电能够实现规模化、产业化利用生物质能，同时也是CO2减排量最大的一种利用形式。但大部分农林生物质具有较高的碱金属、碱土金属以及氯元素，燃料灰熔点较低，会带来锅炉受热面积灰腐蚀、结渣沾污等问题[2]。因此，对于流化床生物质燃烧过程中的流动、传热和反应特性进行深入研究具有重要意义。

鉴于热态实验中参数测量和表征的困难，数值模拟方法已经成为探究稠密气固系统的过程特性和反应机理时不可缺少的手段。基于计算流体动力学（computational fluid dynamics，CFD）的数值模拟方法主要有三种：双流体模型（two-fluid model，TFM），CFD–DEM 和多相流质点网格法 （multi phase–particle in cell，MP–PIC）。TFM中颗粒相被视为拟流体，计算效率较高，但无法获得颗粒层面上的运动与热质传递信息；MP–PIC方法中颗粒相保持了离散颗粒特征，颗粒成团和碰撞力模式化方法有利于计算速度的提高，但该方法同样无法获得单颗粒尺度上的受力、传热和反应机制；CFD–DEM法可以追踪系统里的每一个颗粒，直接计算颗粒受到的碰撞力、热传导和参与的化学反应，缺点是计算所耗费的时间较长。近十年来，随着计算机硬件的迅速发展和模型的不断优化，国内外已有学者将CFD–DEM方法应用于流化床生物质/煤颗粒的燃烧和气化过程。现有研究主要集中于模型构建与验证[3-4]，气化/燃烧特性随参数的变化[5-6]和颗粒温度演化规律等[7-8]。而对于流化床内传热机制的研究相对较少，CFD–DEM尤其适用于颗粒尺度传热的研究，可以有效弥补实验测量方法的不足。Zhou等[9]模拟了鼓泡流化床的流动与传热过程，分析了颗粒–颗粒导热、气固对流传热、颗粒辐射等对总热流的贡献。Hou等[10]对于不同流化形态下的颗粒传热特性进行了研究。Hu等[7]对鼓泡床煤燃烧进行了数值模拟，考察了二次风对传热特性的影响。Wang等[11]则初步研究了流化床中焦炭燃烧过程的传热和传质特性。

本文采用CFD–DEM法耦合热化学模型，对鼓泡流化床生物质燃烧过程中的传热特性进行了研究，传热子模型包括颗粒–颗粒传热、颗粒–壁面传热、气固对流传热、辐射传热和反应放热。重点分析了不同传热模式对于生物质/床料颗粒传热过程的贡献，以及反应器内热点温度的产生与演化规律。

1 数学模型

1.1 气相控制方程

在CFD–DEM框架下，气体相基于欧拉法，湍流运动采用标准k–ε湍流模型描述。均相反应的质量传递通过组分输运方程的源项实现，非均相反应产生的质量、动量、能量传递通过各自守恒方程中的源项实现。具体的气相场控制方程和说明详见文献[12-13]。

1.2 颗粒相控制方程

颗粒运动包括平动和转动两种方式，遵循牛顿第二定律。颗粒碰撞模型采用软球模型，即通过弹簧、阻尼器和摩擦块三种力学模型来模拟颗粒间接触作用。颗粒运动方程与受力分析为[12]

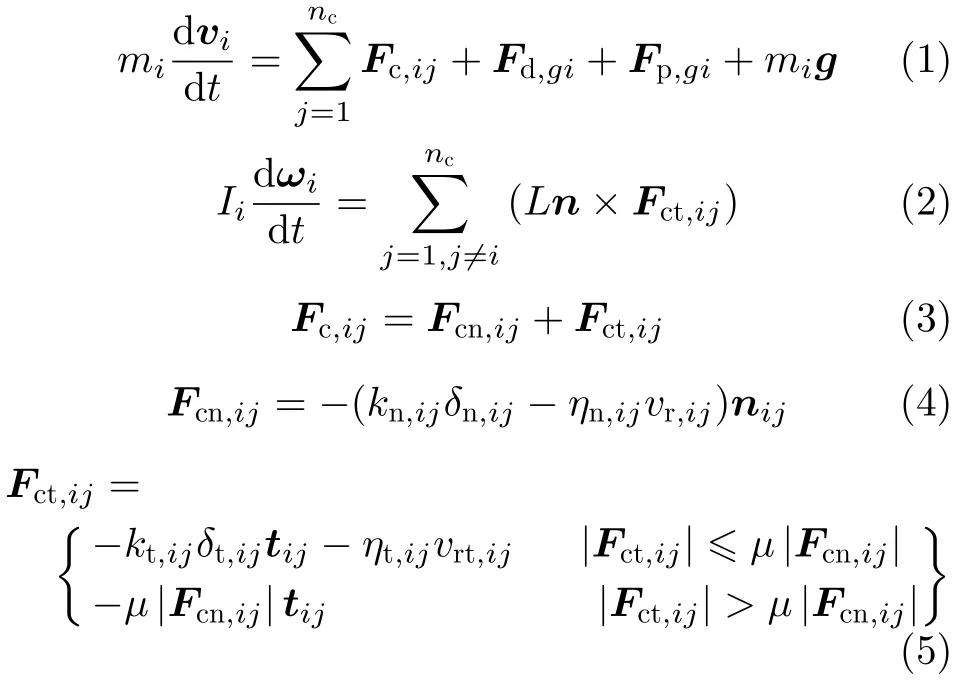
式中，mi为颗粒质量；Fc,ij,Fd,gi和Fp,gi分别为颗粒所受的碰撞力、气固曳力和压力梯度力；Ii，ωi和L则分别为颗粒的转动惯量、角速度、接触点与颗粒中心的长度；δ 是碰撞切向力产生的颗粒位移；vr,ij为颗粒i相对颗粒j的速度矢量；nij为单位法矢量；μ为摩擦系数；vrt为切向的相对速度；k和η 分别是刚性系数与阻尼系数，本文根据LSD (linear spring dashpot) 接触模型进行计算。

在传热模型方面，本文新引入了颗粒–壁面导热子模型，颗粒的能量守恒方程为[14]

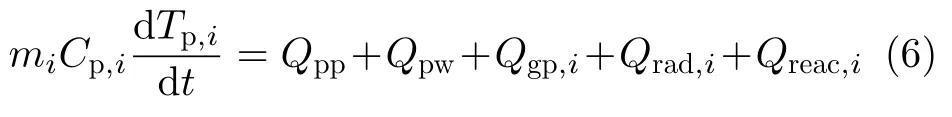
式中m，Cp和Tp分别为颗粒质量、比热和温度。Qpp为颗粒与颗粒间的导热，包括颗粒间直接接触导热 (Qpp,ij) 和颗粒–流体–颗粒间的非直接接触导热 (Qpp,igj) ；Qpw为颗粒–壁面的导热，同样包括直接 (Qpw,iw) 与非直接接触导热 (Qpw,igw) ；Qgp和Qrad分别代表气体与颗粒间的对流传热和颗粒与周围空间的辐射传热量，Qreac为气固非均相反应产生的热量变化。颗粒–壁面导热与颗粒–颗粒导热的计算方法基本一致，只需将壁面处理成具有无限大直径和质量的颗粒。四种传热量的计算表达式分别为[14]

式中，λp和hgp分别为颗粒热导率和对流传热系数，αg为气体体积分数，Tenv为颗粒周围的环境温度，Np,Ω为Ω范围（网格）内的颗粒数量，Cs为燃料颗粒浓度，ΔHrs为反应热。

1.3 化学反应模型

流化床生物质燃烧过程中发生的化学反应主要包括燃料热解、半焦燃烧、挥发分燃烧、气态污染物生成与转化等。为简化模型，本文忽略生物质中的氮和硫元素，且假设半焦为纯碳颗粒。热解释放挥发分的组分平衡方程为

式中，各组分质量分数v1～v8的数值，根据热解的实验结果和元素守恒计算确定[15]。热解速率表达式为

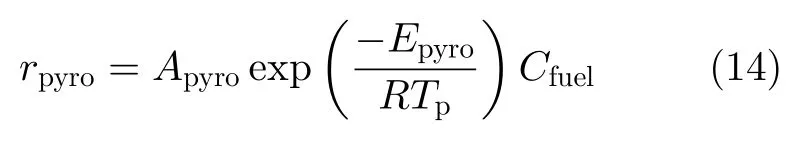
式中，Cfuel为燃料颗粒摩尔浓度。前指因子Apyro=8.276×104s–1，活化能Epyro= 7.3×107J/kmol[11]。

半焦颗粒的燃烧反应方程式为

颗粒反应模型采用缩粒模型，即燃料颗粒半径随着反应的进行逐渐减小。半焦燃烧速率由Arrhenius反应动力学速率Rchem与气体扩散速率Rdiff共同控制，表达式为[11]

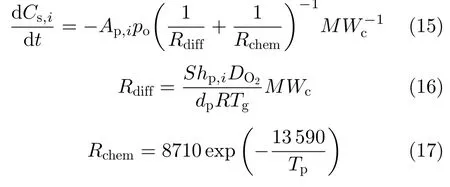
式中，Ap,i，po和MWc分别为颗粒表面积、氧气分压和半焦摩尔质量。Shp,i是Sherwood数，DO2为氧气扩散系数。

在目前的反应模型中，气体均相反应则包括了CO，H2，CH4和焦油的氧化反应，化学方程式和反应速率表达式如表1所示。

表1 化学反应方程式和反应速率[11]Table 1 Chemical equation and reaction rate[11]

1.4 模拟对象及参数设置

本文模拟对象为实验室规模的鼓泡流化床燃烧炉[7]，为减少计算量，反应器简化为准三维床体，尺寸为0.066 m×1.6 m×0.003 6 m（宽×高×厚），对应的网格数为22×220×2，反应器结构如图1所示。燃料为生物质颗粒，从右墙连续进料，化学性质如表2所示；床料为石英砂，初始床高0.14 m，共约83 700个颗粒。流化气体为空气，一、二次风分别从床底部和左墙进入反应器，风量比为0.81∶0.19。所有壁面均设置为非滑移边界，前后壁面为绝热边界，左右壁面为恒温边界（1 123 K），顶部为（大气）压力出口。气固时间步长在计算过程中会根据收敛情况自动调整，其中颗粒时间步范围在 1×10–6～5×10–6s之间。该算例在一个intel 12核24线程计算节点上并行计算40 s大约需要30天。详细的气固热物理性质和模拟参数如表3所示。

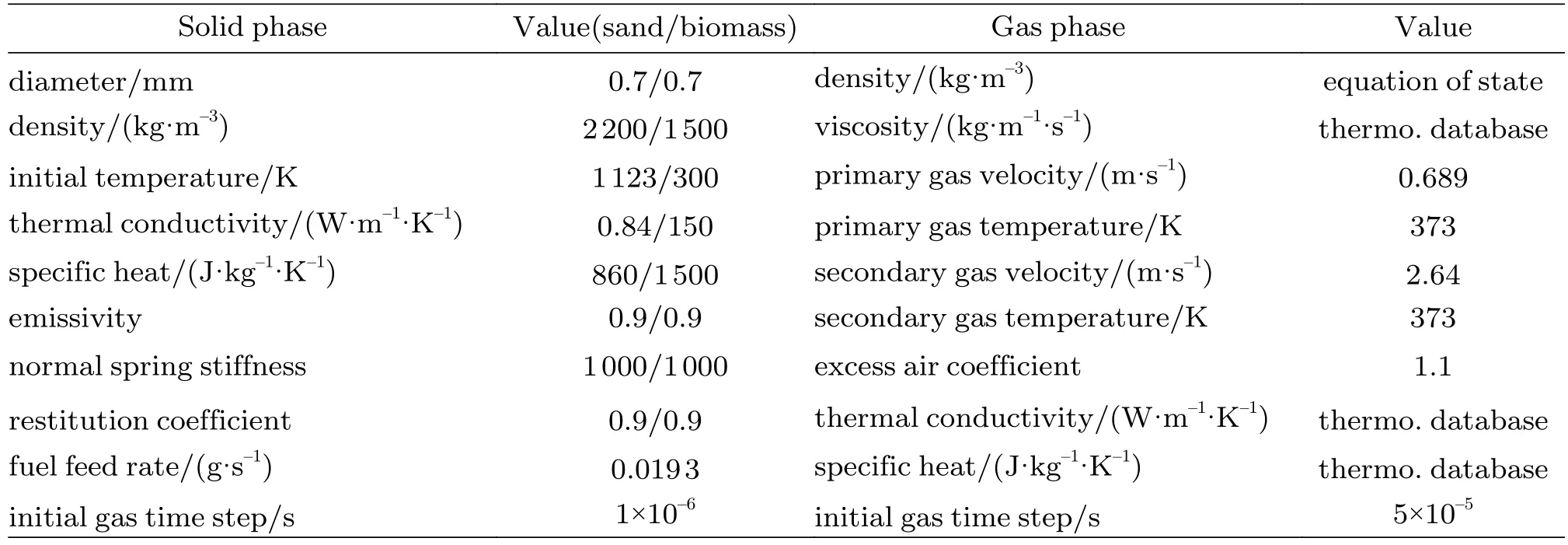
表3 模拟中的物理与数值参数Table 3 Physical and numerical parameter settings of the simulation

图1 流化床反应器结构示意图Fig.1 The schematic diagram of geometry of fluidized bed

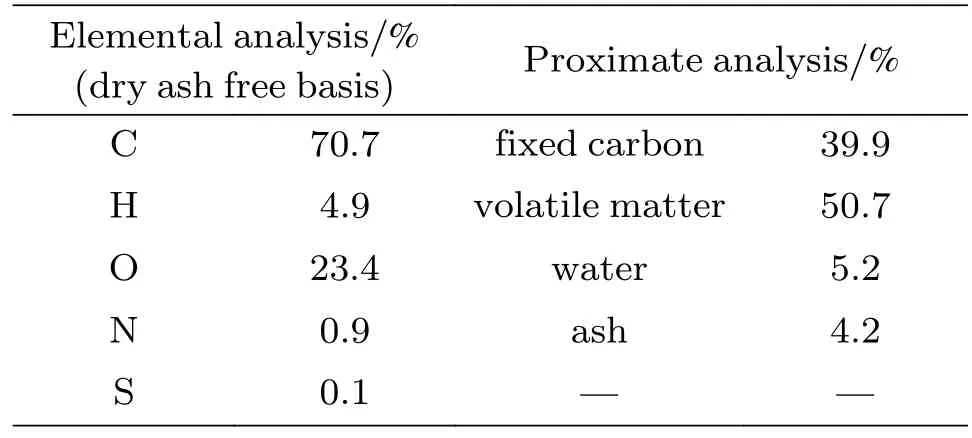
表2 生物质颗粒性质Table 2 Properties of biomass particle

2 计算结果与分析

本文所采用的“CFD–DEM+传热+化学反应”的三维数理模型，已应用于鼓泡流化床半焦燃烧的数值模拟[3]。通过颗粒温度、出口气体组分等模拟值与实验结果的比较表明，建立的模型可以较为准确地预测典型的流动、传热与反应特征。本文的主要目的在于量化不同传热模式在总传热量中的占比，并且通过引入颗粒–壁面传热模型，分析其对于颗粒传热过程的影响，因此省去了模型验证环节。

2.1 气固流型与组分浓度

鼓泡流化床内颗粒流型随时间的变化如图2所示，其中颗粒颜色代表其温度。由图可见，当流化气体进入反应器后，床层下部迅速出现气泡，随着时间发展，气泡逐渐聚并、上升并破碎；与此同时，床层底部形成新气泡并开始又一个循环。从图2也可看出颗粒温度的演化过程，随着燃烧反应的发生，平均温度逐渐升高，且由于床内存在强烈的颗粒返混，颗粒温度分布总体较为均匀。

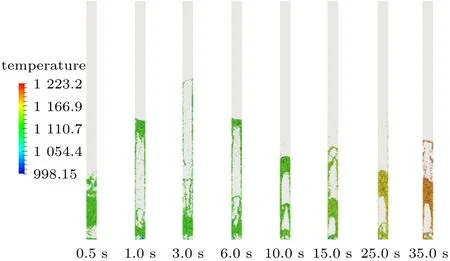
图2 颗粒流型的演化Fig.2 Development of particle flow pattern

图3所示为流化床内的空隙率、气体温度和主要气体组分浓度（O2，CO，CH4和CO2）分布，所有数值均为稳定状态下的时间平均值（35～40 s）。由图可见，床内呈现出典型的“上稀下浓，中低边高”的颗粒浓度分布。气体温度的分布总体较为均匀，自由区域的温度略高于浓相区。由于热解反应的发生，CH4和CO等挥发分气体在右下部进料口附近迅速释放，质量浓度较高，随着燃烧反应的进行，其浓度迅速下降。同时，由于焦炭燃烧主要发生在床层底部，此处也具有较高的CO浓度。另一个值得注意的现象是，O2和CO2浓度的分布基本完全相对，表明CO2几乎全部来自于焦炭和挥发分的燃烧反应。

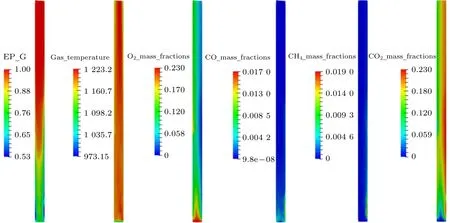
图3 空隙率、气体温度与组分浓度的分布Fig.3 Distributions of voidage, gas temperature and composition concentration

2.2 传热模式

图4所示为不同传热模式产生的颗粒热流量随时间的变化。为了清晰地展示五种传热机制的贡献，本文对燃料和床料颗粒分开讨论，且图中给出了稳定状态下的热流量平均值。由图4(a)可见，在初始阶段，由于生物质颗粒温度较低（300 K），对流和辐射传热的热流量较高，随着床内颗粒的上升、碰撞和气体的返混运动，气固相间和相内的温度差逐渐减小，对流和辐射传热的占比逐渐减小。反应热则呈现相反的分布，其热流量开始较低，随着燃烧反应的发生迅速增加，并最终呈现较为稳定的状态。颗粒–颗粒、颗粒–壁面导热的热流量总体较低，且波动较大，主要是由于导热必须通过颗粒–颗粒或颗粒–壁面的接触进行传导，而颗粒的运动存在随机性和不连续性，因此两种导热模式产生的热流量在总传热量中占比较小。图4(b)所示为石英砂颗粒传热过程中四种传热模式产生的热流量的演化曲线。由于石英砂的初始温度较高（1 123 K），气固对流与辐射传热的热流量总体变化不大，随着燃烧反应的发生，气体和颗粒温度升高，两种传热模式的热流量略有上升。石英砂的颗粒–颗粒、颗粒–壁面导热的热流量的变化规律有所差异，虽然颗粒平均温度略有上升，但由于颗粒温度在床内分布较为均匀，颗粒间的导热总体变化很小；相比之下，由于壁面温度恒定，颗粒–壁面间的导热热流量缓慢上升。

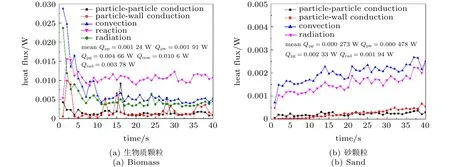
图4 不同传热模式的热流量Fig.4 Heat fluxes of different heat transfer modes

2.3 反应器内热点温度

流化床内热点温度对反应器的稳定安全运行具有重要影响，但截至目前，热点温度的产生和发展机制并不明确，很有必要对此进行深入研究。图5给出了床内热点温度的演化和相应参数分布。由图5(a)可见，随着时间的发展，床内的局部高温从约1 500 K逐渐增加到1 800 K。结合图5(b)的颗粒流型可以看出，热点位置一开始出现在床层表面附近，随着床层高度上升，热点位置逐渐升高，最终出现在自由空域的上部。从图5(c)～图5(f)可以看出，热点温度位置与CH4燃烧速率、CO2浓度的极值位置完全一致，与CO浓度和反应速率极值的位置则相对接近，这是因为CO有一部分由焦炭燃烧产生，而CH4完全来自于挥发分释放。此外，由图5(a)和图5(b)可见，在t=30.33 s和30.34 s时，热点温度附近的颗粒浓度很低，可以推断局部高温主要来自于挥发分气体的燃烧反应，而不是焦炭燃烧反应。

图5 床内热点温度及相应参数的分布Fig.5 Distributions of hot spot and relative parameters

为了进一步分析生物质颗粒温度与颗粒浓度和尺寸的内在联系，图6给出了床内的生物质温度与局部（所在网格）颗粒浓度的分布，圆点的大小表示颗粒尺寸。由图可见，颗粒温度与粒径大小并没有明显关联，在床内的不同区域颗粒分布都较为均匀。颗粒温度与局部颗粒浓度（包含石英砂颗粒）则存在明显的关联，随着颗粒浓度的减小，平均温度逐渐升高，即从浓相区、过渡区到气泡区，生物质温度逐渐增加。这是由于较低的颗粒浓度使得局部的固体热容量较低，容易产生更大的温升。

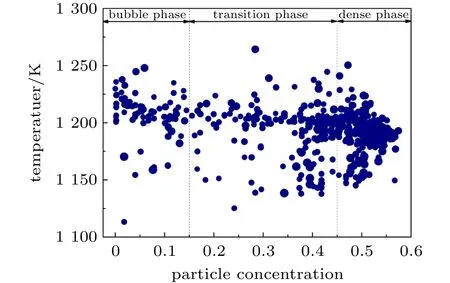
图6 生物质颗粒温度与浓度/粒径的关联Fig.6 Relationship between biomass temperature and particle concentration/size

2.4 挥发分含量对传热的影响

通过上述研究可知燃料的热点温度主要由挥发分气体燃烧产生，为了考察挥发分含量对于传热机制的影响，图7给出了三种燃料稳定燃烧时，不同传热机制在总传热量中的占比。三种生物质颗粒的挥发分含量分别为23%，35%和50.7%，不同工况的过量空气系数保持不变。由图7(a)可见，随着挥发分含量的增加，床内气体的温升更快，气固相间对流传热的热流量及其占比逐渐增加。由于生物质颗粒的初始温度为300 K，当挥发分含量增加，对流传热加强后，生物质温度逐渐上升，其与壁面的温差减小，因此颗粒–壁面的导热占比逐渐减少。此外，较高的挥发分含量容易产生局部热点，导致颗粒与颗粒间的温差增加，即颗粒–颗粒导热占比有所增加。相比之下，挥发分含量对辐射传热和反应热的影响并不明显。总体而言，反应热在燃料颗粒的总传热量中占据主导地位，占比约为47%，对流和辐射传热同样具有重要影响，约占总传热的20%左右，颗粒–壁面和颗粒–颗粒间的导热影响较小，占比分别约为10%和5%。对于砂颗粒来说，四种传热机制占比的变化趋势与生物质颗粒基本一致。对流、辐射、颗粒–壁面导热和颗粒–颗粒导热四种模式分别约占总传热热流量的45%，38%，11%和6%。由此可见，对两种颗粒来说，颗粒–壁面导热的占比均在10%左右，其影响不可忽略。

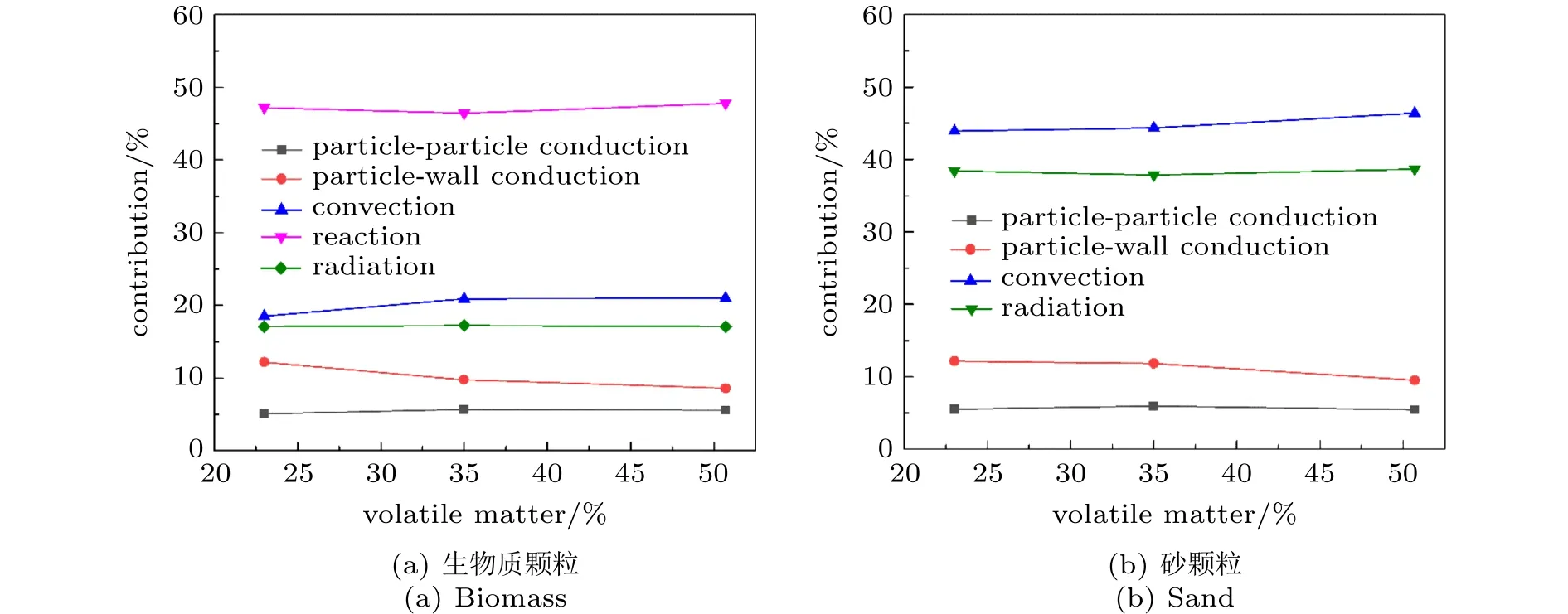
图7 挥发分含量对不同传热机制占比的影响Fig.7 Influences of volatiles contents on the heat transfer modes

3 结论

本文采用CFD–DEM方法耦合热化学模型，新引入了颗粒–壁面导热子模型。对鼓泡流化床内生物质燃烧过程中的颗粒运动、反应特性、传热模式和热点温度等方面进行了研究，并且分析了挥发分含量对不同传热模式的影响，主要结论如下。

（1）CH4等挥发分气体在进料口附近释放，随后浓度迅速下降；而由于焦炭燃烧反应的发生，CO在进料口附近和床层底部都具有较高的浓度。

（2）反应初始阶段的对流和辐射传热的热流量较高，随后逐渐减少；反应热则随着反应的发生逐渐增加并最终呈现相对稳定的值。颗粒–颗粒、颗粒–壁面导热由于属于接触传导，其热流量较低且波动较大。

（3）床内的局部高温主要由挥发分气体的燃烧反应产生，初始出现在床层表面附近，随着气固运动逐渐升高，最终热点温度出现在自由空域上部。生物质颗粒温度与粒径没有明显关联，但随着局部颗粒浓度的减小而逐渐增加。

（4）随着燃料挥发分含量的增加，对流传热、颗粒–颗粒导热在总传热量中所占比例增加，颗粒–壁面导热占比则逐渐减小，辐射与反应热基本保持不变。总体来说，反应热占据主导地位，辐射和对流传热同样起到重要作用，导热所占比例较小，但颗粒–壁面导热不可忽略。