白盒SM4的分析与改进
张跃宇 徐 东 陈 杰
①(西安电子科技大学网络与信息安全学院 西安 710071)
②(桂林电子科技大学广西密码学与信息安全重点实验室 桂林 541004)
③(西安电子科技大学ISN国家重点实验室 西安 710071)
1 引言
传统的密码安全性分析环境被称为黑盒攻击环境,攻击者只能访问密码系统的输入与输出,但随着密码系统部署环境的多样化,该分析模型已经不能够反映实际应用中攻击者的能力。2002年,Chow等人[1]提出了白盒攻击环境的概念,该攻击环境中的攻击者对算法运行环境具备完全的控制权,并且完全掌握算法的设计细节。白盒攻击环境中攻击者的能力包括但不限于:动态观测算法程序运行过程、修改算法程序运行过程中的中间值、对算法程序进行调试分析等。
为了保证在白盒攻击环境下运行的密码算法的密钥安全性,需要对密码算法进行白盒化处理,处理后的算法称为密码算法的白盒实现。密码算法的白盒化方法由Chow等人[1]首次提出,并在其白盒高级加密标准(Advanced Encryption Standard,AES)、白盒数据加密标准(Data Encryption Standard, DES)[2]方案中应用,后续提出的大部分密码算法的白盒实现方案都采用了该白盒化方法。对于白盒实现的安全性分析工作,主要分为两类:一类以Billet等人[3]提出的 BGE分析,Michiels等人[4]提出的 MGH分析为代表。这一类的分析充分地利用了攻击者在白盒攻击环境中所掌握的能力,通过对算法细节的分析找出算法的安全性缺陷,选择特定的查找表并采用仿射等价、线性等价等代数手段剥离算法内部的混淆手段,对混淆剥离后的查找表进行分析提取密钥。这一类的分析方法要求攻击者对白盒实现的设计细节完全掌握,并且需要利用大量的代数方法进行分析,整体的分析难度较高,在实际应用环境中较难进行部署。另一类白盒实现的安全性分析工作以Bos等人[5]于2016年提出的差分计算分析(Differential Computational Analysis, DCA)为代表。DCA是差分功耗分析[6]的软件版本,DCA不需要攻击者掌握算法的设计细节,只需要采集算法程序在运行过程的中间状态,通过相应的统计分析方法提取密钥。相较于BGE,GH等分析手段,DCA分析只需要掌握白盒实现的底层算法,能够监测白盒实现程序的运行过程即可进行分析,极大地降低了分析的部署难度。
DCA的提出将白盒实现的安全性分析工作自动化、简单化。由于其便捷性与高效性,DCA自提出之后便获得了广泛关注。Bos等人[5]只是提出了DCA,并利用该方法对几个白盒AES实现进行了成功分析,并未在理论层面对DCA进行解释说明,文献[7,8]对DCA进行了详细的解释与介绍,并分别给出了该分析能够成功进行的理论原因。文献[9]又提出了改进DCA分析效率的方法。2019年,Rivain等人[10]讨论了内部编码对于DCA的影响,并提出了一种与差分计算分析类似的分析手段。同年,Bogdanov等人[11]又提出了高阶的差分计算分析方法,用以分析包含软件补偿对策的白盒实现。
在差分计算分析的理论不断改进与发展的同时,研究人员也在寻找针对该分析的软件补偿措施,用以减轻甚至消除差分计算分析对白盒实现安全性的影响。Biryukov等人[7]中提出了名为掩蔽(masking)的补偿手段,掩蔽可用于计算过程中的中间值也可用于算法的结构。Lee等人[12]于2017年提出了基于Chow白盒AES改进的白盒AES实现方案,该方案在查找表输出中添加随机掩码用以抵抗差分计算分析。同年,Banik等人[13]提出了控制流混淆、查找表位置随机化、虚拟操作等软件补偿措施以对抗DCA。2020年,Lee等人[14]再次提出了一种改进型的白盒实现方案,该方案主要针对高阶差分计算分析而改进。在不断地对抗与改进中,差分计算分析已成为检验白盒实现方案安全性的重要工具。
SM4算法(原SMS4算法)是我国商用密码标准算法[15]。肖-来白盒SM4是SM4算法的第1个白盒实现方案[16],该方案采用了Chow等人的白盒化思想。2013年,肖-来白盒SM4方案被林婷婷等人攻破[17]。2015年,Shi等人[18]提出了一种新的白盒SM4方案,该方案将SM4步骤结合到查找表中,并采用随机混淆对查找表进行保护。同年,Bai等人[19]提出了白-武白盒SM4实现方案,该方案在肖-来白盒SM4的基础上将线性编码复杂化,希望以此提高方案安全性。2018年,潘文伦等人[20]对肖-来白盒SM4与白-武白盒SM4方案进行了成功分析,分别给出了两个方案的密钥空间大小,同时证明了复杂化的线性编码对方案安全性的贡献是有限的。2020年,姚思等人[21]结合混淆密钥与查找表技术提出了一种内部状态扩充的白盒SM4实现方案 (White-box implementation of SM4 algorithm with Internal State Expansion, WSISE)算法,该方案显著提高了攻击者提取密钥的复杂度。
本文在差分计算分析的基础上提出了中间值平均差分分析(Intermediate-Values Mean Difference Analysis, IVMDA),本分析以白盒SM4实现加密过程中的所有查表结果为输入,分析以脚本程序的形式部署,分析过程自动化进行。攻击者只需控制白盒实现的运行环境即可进行分析。利用IVMDA成功对肖-来白盒SM4进行了密钥提取工作。为了保证白盒SM4方案的安全性,在肖-来白盒SM4方案中增加软件对策以抵抗IVMDA。经实验验证,改进后的白盒SM4方案可以有效抵抗IVMDA。
2 白盒SM4方案
肖-来白盒SM4实现方案在保持标准SM4算法整体结构不变的同时,将每一轮中密钥相关的步骤用查找表的形式表示。采用线性编码对查找表的输入输出进行混淆,并且上一个变换的输出部分引入的混淆会在下一个变换的输入部分被抵消,以保证白盒SM4方案与标准SM4的输入输出一致。方案中的线性编码均采用仿射的形式。肖-来白盒SM4方案的一轮的计算过程如图1所示。肖-来白盒SM4方案的一轮加密过程包含5个复合仿射变换,4个8~32 bit的查找表,6个异或操作。

图1 肖-来白盒SM4的一轮计算过程



3 白盒SM4的中间值平均差分分析
差分计算分析是差分功耗分析在白盒攻击环境下的软件版本,该分析以算法程序运行过程中的软件执行轨迹(software execution trace)为分析对象,而根据软件执行轨迹的具体种类以及进行统计分析时所采用的方法的不同,差分计算分析也可被分为不同种类,差分数据分析[22](Differential Data Analysis, DDA)便是其中一种。本文在差分计算分析的基础上提出了一种针对白盒SM4方案的分析方法,称为中间值平均差分分析。
3.1 中间值平均差分分析
为了提高分析效率,选择白盒实现程序的所有查表结果为分析对象,采用均值差分作为密钥与软件执行轨迹的相关性指标,由于白盒实现中查找表部分采用了线性编码对结果进行混淆,因此在分析过程中添加线性组合步骤来抵消编码影响,分析步骤与DCA基本一致。将该分析方式命名为中间值平均差分分析(IVMDA)。IVMDA的目标是能够在实际的应用环境下对白盒SM4实现进行密钥提取,因此攻击者的能力需要符合实际的应用场景。基于以上考虑,攻击者被定义为一个具有恶意目的的合法用户,该用户以提取嵌入白盒实现程序中的密钥为目标,掌握白盒实现程序及其部署环境,同时具备一定的逆向工程能力、代码调试能力等黑客技能。攻击者不掌握白盒实现算法的设计细节,只了解白盒实现算法的底层算法。对于包含外部编码的白盒实现程序,攻击者不掌握外部编码,但可以以合法用户身份向外部编码发起问询,并获得编码后的明文。
IVMDA整体分为两部分,数据采集部分与分析部分。



改变攻击点,对第1轮中剩余3个包含轮密钥加的S盒运算执行以上分析步骤,即可提取出一轮的轮密钥。整个的分析流程可以自动化进行。后续轮次的密钥值的计算可在已提取密钥值的参与下采用IVMDA对每一轮中包含轮密钥信息的S盒进行分析而得到。
综上,IVMDA采用查表结果作为分析对象,相较于DCA省略了对软件执行踪迹进行序列化处理的步骤,分析过程更加精简,并且分析对象的采集方式会更多样,所需采集的数据量也更小。采用均值差分作为密钥与软件执行踪迹之间的相关性指标,相较于DDA所采用的皮尔逊系数,分析步骤的复杂度更低。采用线性组合的方式抵消白盒方案中的线性编码混淆作用,保证了分析的正确性与改进后的DCA相当。
3.2 对肖-来白盒SM4的中间值平均差分分析实验



图2 肖-来白盒SM4的中间值平均差分分析结果

(1) 对当前的可能密钥计算60次中间函数,包含60次S盒运算,3×60=180次8 bit向量的异或运算;
(2) 计算60个中间函数结果的所有线性组合值,即执行60×255次8 bit向量乘法,每一个中间函数结果对应255个线性组合值,记作B;
(3) 根据B中相同位置上的元素值,将B对应的中间函数结果所对应的中间数据流进行分组,共进行255×60次分组;
(4) 每一次分组之后,计算不同分组之间的均值差分,该过程中执行包含128个元素的集合的异或255×58次,除法运算255×2×128次,128个元素的集合对应元素差分运算255次;
(5) 进行完(4)中的运算后,得到255个包含128个元素的差分值集合,选择其中最大差分值作为ΔKey。
执行以上5部分运算256次即可计算出所有可能密钥的ΔKey值,取最大ΔKey对应的假设密钥值作为最佳密钥猜测。第1轮中4个8 bit密钥的计算均采取相同的办法。
综合实验结果来看,中间值平均差分分析能够成功地对肖-来白盒SM4进行密钥提取工作,只需掌握白盒实现程序及其部署环境,分析过程被封装为一个脚本程序,在实际的应用环境中很容易进行部署。相较于传统分析方法中所常用的求解矩阵方程、差分分析法等计算方法,IVMDA在分析时所采用的计算均为常见的简单运算如异或、除法、差分等,计算的复杂度大大降低。综上,IVMDA是一种非常高效的白盒SM4方案分析方法,其对于白盒SM4安全性具备实际性的威胁。
4 非线性混淆的白盒SM4方案
为了抵抗IVMDA,在肖-来白盒SM4实现方案中添加软件对策,利用非线性编码对查找表的输出进行混淆,消除查表结果与密钥之间的相关性,本节提出非线性混淆的白盒SM4实现(White-Box SM4 with Nonlinear Confusion, WBSM4-NC)方案。
4.1 非线性混淆的白盒SM4实现方案
IVMDA能够成功提取密钥的原因在于查找表的输出值与密钥之间存在相关性,并且线性编码的混淆作用可以通过计算线性组合的方式进行抵消。本节所提非线性混淆的白盒SM4实现方案在查找表的输出处添加非线性编码,对查找表结果进行混淆。添加混淆之后的查找表结构如图3所示。
图3中xi,j表示第i轮中第j个查找表的输入,Ei,0消 除xi,j中的编码。S*为包含轮密钥加操作的S盒。Ri,j为8~32 bit的仿射编码,是原方案中矩阵L与仿射变换Qi的复合编码Ri的一部分,当j=0,1, 2时Ri,j,以矩阵形式执行编码操作,当j=3时Ri,j以仿射变换形式执行编码操作。out为添加的8 bit非线性编码,对查找表输出再次进行混淆。图3所示的查找表结构是在肖-来白盒SM4方案的查找表结构的输出部分添加了4个级联的8 bit非线性编码,对Ri,j表的32 bit输出进行混淆。经过混淆的32 bit结果作为该表的输出,这样使得输入xi,j与经过混淆的32 bit结果对应起来,形成了新的带有非线性混淆的8~32 bit的查找表。
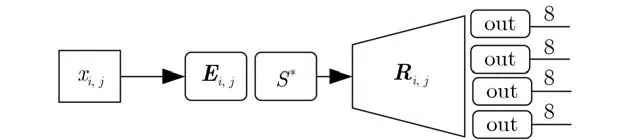
图3 包含混淆操作的查找表
在使用8 bit非线性编码对查找表的输出进行混淆之后,不能直接使用查表结果进行异或。异或过程需要借助异或表完成,异或表结构如图4(a)所示。异或表以两个字节为输入,表中输入编码in消去数据中的非线性编码。in=out–1,异或后的数据需要再进行编码保护,确保再次与其他数据进行异或时的正确性。肖-来白盒实现中4个查找表结果的3次异或操作需要用12个异或表来替代,最终结果为一个32 bit的经过4个级联的8 bit非线性编码的结果,即该结果为图1中的Y 进行4个级联的8 bit非线性编码操作,记作Y′。


图4 异或表与编码过程

4.2 非线性混淆的白盒SM4实现方案的分析与对比



图5 查找表与部分仿射编码的组合

在应用潘文伦等人的分析方法对WBSM4-NC的安全性进行分析的过程中,对Qi矩阵部分的恢复也是基于以上原因无法进行,所以同理也可以认为WBSM4-NC方案对于潘文伦等人的分析方法是安全的。
通过以上的分析,WBSM4-NC在已有的针对白盒SM4实现的安全性分析中可以保证安全性,接下来验证该方案在中间值平均差分分析下的安全性。采用与3.2节相同的程序执行环境进行中间值平均差分分析实验,实验结果如图6所示。
分析程序的输出为图6的杂乱折线图,说明本文采用的软件对策可成功抵抗IVMDA。这是由于采用了8 bit的非线性编码对查找表结果进行混淆之后,查找表结果与原密码算法中包含轮密钥加的S盒运算的结果之间的关系相当于执行了一次置换操作,同时也可以采用一些被验证过的S盒来充当该8 bit非线性编码,由于S盒的性质,混淆后的查找表结果与原查找表结果之间的相关性很难采用相应手段进行恢复,从而在IVMDA中保证了方案的安全性。表1对几种白盒SM4实现方案的安全性进行对比。

图6 WBSM4-NC方案的中间值平均差分分析结果

表1 白盒实现方案的安全性对比
从表1的安全性对比可以看出,在安全性方面WBSM4-NC方案相比于其他的白盒SM4方案具备一定的优势。该方案可以抵抗林婷婷等人以及潘文伦等人的分析,在实际的应用环境中能够保证密钥的安全性。下面对WBSM4方案的内存效率进行分析与对比。
为了保证密钥安全性,抵抗IVMDA, WBSM4-NC方案在内存性能上做出了妥协,牺牲内存空间以换取安全性。在每一轮的加密过程中,总计3种不同类型的查找表:
(1)嵌入轮密钥的8~32 bit查找表,每张表占用空间28×32 bit=1 kB;
(2)16~8 bit的异或表,每张表占用空间216×8 bit=64 kB;
(3)8~32 bit的 TDi,j表,每张表占用空间28×32 bit=1 kB。
每一轮包含4张嵌入轮密钥的8~32 bit查找表、12张异或表、4张T Di,j表,因此整个的加密过程中查找表占用的空间为32×4×1 kB+32×12×64 kB+32×4×1 kB=24832 kB。相比于肖-来白盒SM4方案中总大小为128 kB的查找表,WBSM4-NC方案的空间耗费是巨大的。但是需要注意,肖-来白盒SM4方案本身并不包含非线性混淆部件而只有线性混淆部件,因此该方案的空间耗费小于包含非线性部件的方案。表2对几种白盒方案的效率做了简单比较。
表2的Luo-Lai-You白盒AES方案[26]的空间大小与WBSM4-NC方案空间大小处在相同数量级,这是由于这两个方案中均包含非线性混淆,原有的异或操作需要用异或表实现,因此需要占用大量内存空间。同时,Luo-Lai-You白盒AES方案中使用的非线性部件为4 bit,根据文献[8]的研究结论,4 bit的非线性编码并不能混淆软件执行轨迹(该文献中选择内存读取记录为分析对象)与密钥之间的相关性。

表2 白盒实现方案的内存效率对比
为了验证4 bit的非线性部件是否能够混淆查找表结果与密钥之间的相关性,采用了IVMDA对使用4 bit非线性部件的WBSM4-NC方案进行分析,该分析的运行环境与3.2节中IVMDA的运行环境相同,图7是本次分析的输出结果。相对于8 bit的WBSM4-NC方案,4 bit版本方案在构造方法上保持一致,只是由于编码长度的改变,相应的查找表大小与异或次数发生了变化,具体的方案不再展开描述。根据分析结果显示,第1轮中所有部分轮密钥均被揭示。由此可以证明:4 bit长度的非线性编码并不能混淆查找表结果与密钥的相关性,因此使用8 bit的非线性部件是为了保证安全性而作出的必要妥协。
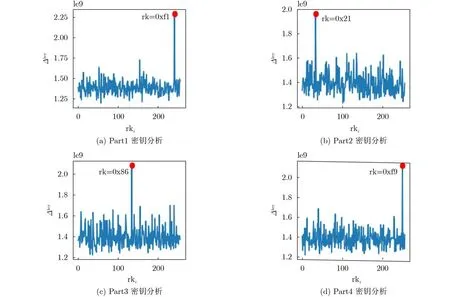
图7 4bit版本的WBSM4-NC方案的中间值平均差分分析结果
白-武白盒SM4方案占用空间较大的原因在于该方案为了提高安全性,在设计编码时使得编码复杂化,查找表数量较多。综上可以看出,白盒方案在确保安全性的同时就必须舍弃一部分内存效率,WBSM4-NC方案的内存开销仍在合理范围之内。WBSM4-NC方案对查找表的输出进行非线性混淆,将部分复合仿射编码以查找表的形式存储,提高了白盒SM4方案的安全性。并且与其他白盒SM4实现方案相比其内存效率也保持在合理范围之内。该方案适合在实际应用环境中部署,以提高密码系统的安全性。
5 结束语
本文针对白盒SM4方案,提出了中间值平均差分分析IVMDA,该分析方法是差分能量分析针对白盒SM4方案的软件改进版本。首次提出白盒SM4方案的自动化分析方法,降低了对白盒SM4方案进行安全性分析的难度。中间值平均差分分析使白盒密码分析工作不再专属于密码学者,掌握部分计算机技能的黑客也可以对白盒密码系统进行分析,这对于白盒密码系统的安全性是一种非常实际的威胁。同时,考虑到IVMDA针对查找表的输出结果进行分析,利用计算线性组合的方式抵消线性编码对查找表结果与密钥相关性的混淆,该分析主要针对的是采用线性编码保护查找表的白盒方案。后续的研究工作可以将中间值差分分析拓展到其他采用线性编码保护查找表的白盒实现方案上,形成一个普适性的分析框架,以更好地评价白盒方案在实际应用环境中的安全性。本文提出了利用8 bit非线性编码对查找表输出进行混淆的软件对策来抵抗IVMDA,提出非线性混淆的白盒SM4实现方案WBSM4-NC。通过实验验证,该软件对策可以有效抵抗中间值平均差分分析。但为了保证安全性,必须增加白盒实现方案的内存占用,这同时也相应地限制了白盒实现方案的应用范围。因此,在后续的研究中需要进一步地探究如何在保证安全性的前提下,降低白盒实现方案的内存开销,这对于白盒密码的实际应用具有重要意义。

