稀疏贝叶斯字典学习空时机动目标参数估计算法

章 涛 张亚娟 孙 刚 罗其俊

(中国民航大学天津市智能信号与图像处理重点实验室 天津 300300)

1 引言

机载雷达具有覆盖范围广、探测距离远、抗干扰能力强的优点，是现代战争中获取情报信息不可或缺的技术装备之一。但机载雷达平台处于高空，一般工作在下视状态，运动目标常常淹没于地杂波中。由于载机平台运动，使得地杂波多普勒谱展宽，单一多普勒域滤波方法难以抑制机载雷达地杂波。空时自适应处理(Space-Time Adaptive Processing，STAP)利用地杂波的空时耦合特性，在空间和时间上进行空时2维联合自适应滤波，能对地杂波进行有效抑制的同时保证对目标足够的增益，已成为机载阵列雷达信号处理的重要方法[1，2]。机动目标跟踪是雷达信号处理领域的难点问题，在发现目标后获取目标的速度、加速度等参数对改善机动目标跟踪性能具有重要意义[3，4]。当雷达发射频率固定时，加速度恒定的机动目标回波信号为线性调频信号，因此机动目标参数估计问题可转化为线性调频信号参数估计问题[5，6]。一些研究人员将时频分析方法如Winger-Ville分布[7]、短时傅里叶变换[8]、分数阶傅里叶变换[9]等线性调频信号参数估计方法应用于机动目标的速度、加速度等参数估计，在脉冲数较多的情况下取得了较好的估计效果。

近年来，稀疏恢复理论在信号处理领域快速发展，能够在较少脉冲数情况下高精度地恢复稀疏信号，已成为机动目标参数估计领域的研究热点。文献[10]利用梯度投影稀疏重构方法实现了地基雷达机动目标的加速度估计。文献[11]利用基追踪(Basis Pursuit， BP)方法对机动目标的方位角、速度及加速度参数进行稀疏恢复。文献[12]首先利用3次相位函数将机动目标回波信号中的加速度和速度项分离，然后利用两次1维稀疏恢复分别估计加速度和速度。上述基于稀疏恢复的机动目标参数估计方法，将机动目标回波信号看作在某些参数构成的基向量下是稀疏的，这些基向量被称为字典[13]。由于字典是有限且离散的，稀疏恢复时机动目标参数空间需要进行离散化处理[14]。离散化的字典与机动目标加速度和速度连续参数间的误差问题被称为字典失配问题，严重影响稀疏恢复效果[15，16]。虽然通过增加离散化的字典密度可以减少字典失配误差，但是过于密集的字典网格会导致字典中基向量的相关性过强，从而降低稀疏恢复的性能。针对稀疏恢复中字典失配问题，文献[17]提出了一种稀疏总体最小二乘方法，结合动态字典模型解决1维波达方向(Direction Of Arrival， DOA)估计中的字典失配问题。文献[18]提出利用基追踪方法解决DOA估计中的字典失配问题。为了避免正则化参数难以确定的问题，文献[19]提出了利用动态字典的稀疏贝叶斯学习DOA估计方法。

针对稀疏恢复机动目标参数估计在存在字典失配情况时性能严重下降的问题，本文提出一种基于稀疏贝叶斯字典学习的空时机动目标参数估计方法。本方法首先通过目标方位信息补偿多个阵元数据构建联合稀疏恢复数据，然后对补偿后的每个阵元数据利用双线性相位变换进行加速度和速度项分离，最后利用泰勒级数分别构建加速度参数和速度参数的动态字典，并将参数失配误差作为待估超参数构建贝叶斯稀疏恢复模型，获得稀疏支撑集及参数失配误差后即可得到机动目标加速度和速度参数估计值。

2 信号模型及字典失配问题

2.1 信号模型

2.2 字典失配问题

目前已有的稀疏恢复机动目标参数估计方法使用固定离散化的参数空间构建稀疏恢复字典，即目标加速度和速度参数只能在离散数值上稀疏恢复。但是机动目标的加速度和速度参数均为连续变化参数，当参数真值不在离散化的参数空间上时，稀疏恢复中的字典失配误差将严重影响目标参数估计的精度。图1(a)为目标参数恰好位于字典网格点上的示意图，图1(b)为目标参数偏离字典网格点即存在字典失配的示意图。虽然通过增加离散化的字典密度可以用来减少字典失配误差，但是过于密集的字典网格会导致字典中基向量的相关性过强，从而降低稀疏恢复的性能[15]。

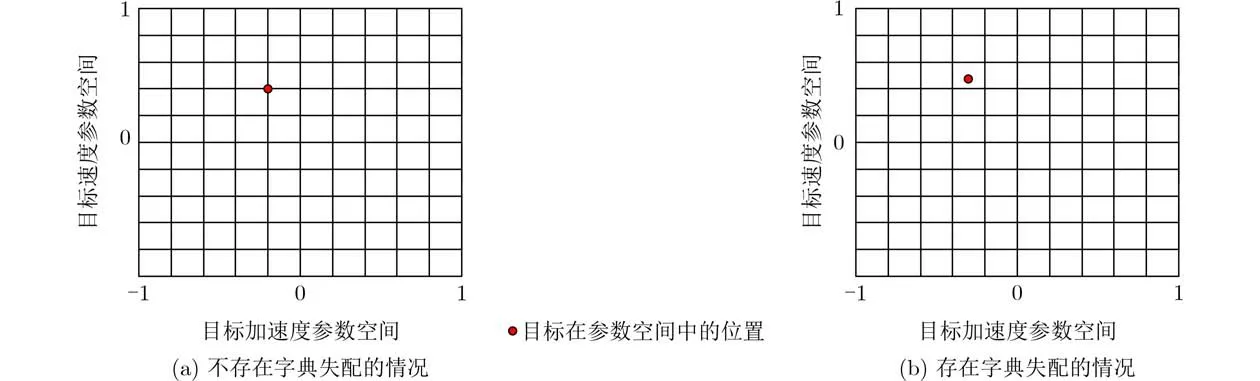
图1 目标在参数空间中位置示意图

3 稀疏贝叶斯字典学习参数估计方法

3.1 多通道空域数据相位补偿构建联合稀疏恢复模型

由于机动目标一般仅存在于一个距离单元中，因此已有稀疏恢复参数估计方法仅利用单个观测向量进行稀疏恢复，而多个观测向量的联合稀疏恢复能够显著提高稀疏恢复的性能[13]。机载阵列雷达每个阵元分别进行脉冲采样，获得多通道空域采样数据，因此本文将多通道空域采样数据进行相位补偿进而构建目标参数估计的多个多普勒观测向量。利用式(9)进行空域相位补偿可获得M个多普勒频率观测数据。相位补偿前后的空时采样示意图如图2所示。

图2 相位补偿前后的空时采样示意图

3.2 机动目标加速度估计

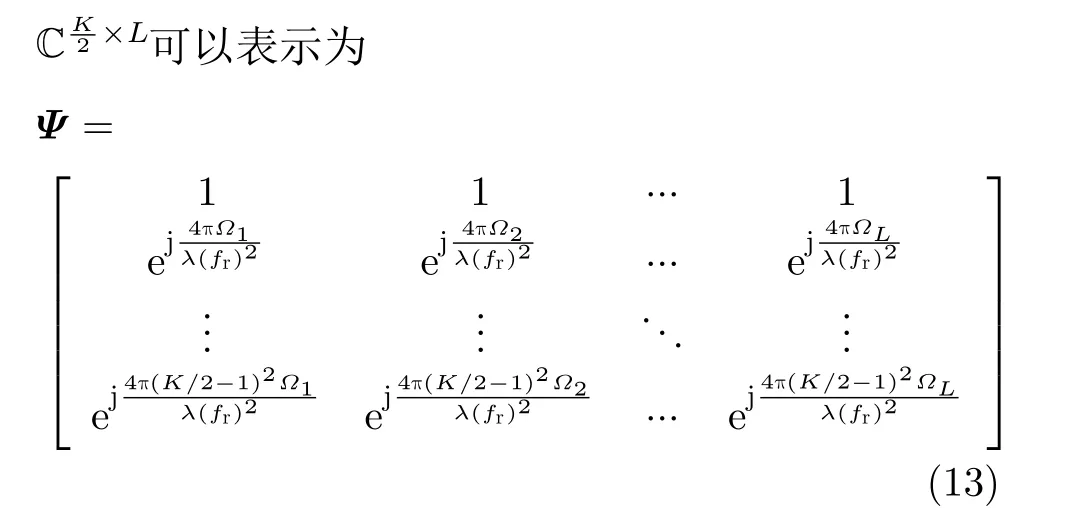
Ω={Ω1，Ω2，...，ΩL}代表预先离散化的机动目标加速度参数空间，由于机动目标的加速度为连续变化参数，当目标加速度值不在离散化的参数空间上时，字典失配误差将严重影响目标加速稀疏恢复精度。因此本文利用动态字典模型，将字典失配误差作为待估超参数，构建贝叶斯稀疏恢复模型进行加速度估计。

atΩΩatΩl，l ∈{1，2，...，L}

假设目标加速度 不在预先离散化的加速度参数空间 中，若参数空间 中与 最近的为 ，则包含字典失配误差的动态字典矢量用1阶泰勒级数展开形式近似为

进行字典失配补偿后，式(12)改写为

3.3 机动目标速度估计

重新构造目标速度估计的初始稀疏恢复字典

再利用与3.2节相似的方法获得机动目标速度估计值。

3.4 算法步骤

4 仿真实验

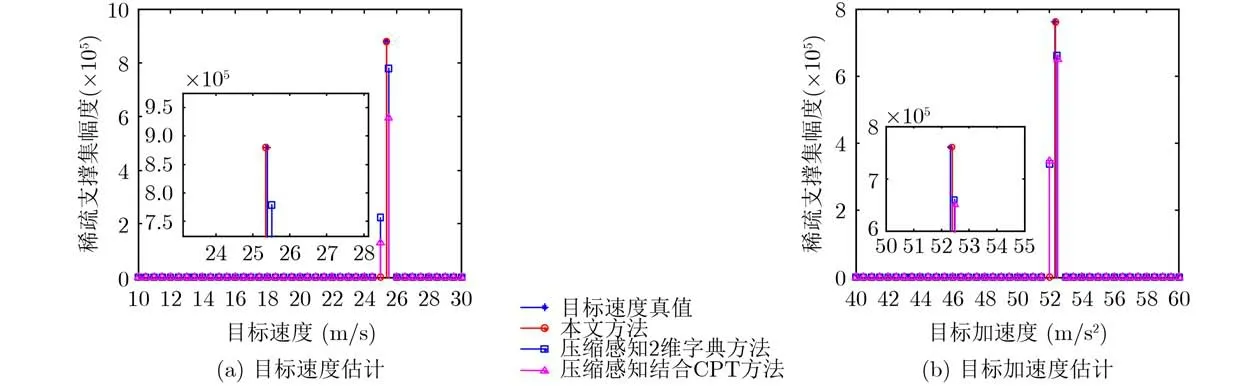
图3 字典失配情况下的目标参数估计结果

实验2 设置阵元数分别为8，16和32时进行目标参数估计。速度估计字典在1 0～30 m/s范围字典间隔分别取0.2 m/s。图4为不同阵元数情况下各种方法估计得到的目标速度估计误差随信噪比变化的曲线。从图4(a)可以看出随着阵元数增加本文方法的速度估计均方根误差不断减小，因此可以证明，本文对多通道空域采样数据进行相位补偿进而构建速度估计的多观测向量联合稀疏恢复，可以有效提高目标速度估计性能。而从图4(b)和图4(c)可以看出，尽管阵元数增加，但2维字典压缩感知方法和压缩感知结合3次相位变换方法都使用单个观测向量进行稀疏恢复，因此估计误差较大且不随阵元数增加而明显变化。

图4 不同阵元数时目标速度估计均方误差随信噪比变化情况

图5为不同阵元数情况下各种方法估计得到的目标加速度估计误差随信噪比变化的曲线，字典在40～60 m/s2范 围字典间隔取0.2 m/s2，存在字典失配问题。从图5(a)中可以看出当阵元数增加时，本文方法的目标加速度估计性能明显提高，这是由于多观测向量能够明显提高稀疏恢复性能。而对比方法没有构建多观测向量稀疏恢复，所以阵元数的增加对估计性能影响很小，如图5(b)和图5(c)所示。

图5 不同阵元数时目标加速度估计均方误差随信噪比变化情况

实验3 设置不同字典间隔用以验证不同字典失配程度下各种方法的估计性能。速度估计时，在10～30 m/s 范围字典间隔分别取0.1 m/s ，0.2 m/s和 0.5 m/s构造稀疏恢复字典，即字典间隔越大字典失配问题越严重。图6为本文方法与对比方法估计得到的目标速度估计误差随信噪比变化的曲线。在3种字典间隔取值的情况下，本文方法的参数估计性能都优于对比方法，更接近目标参数估计的CRB。对比图6(a)–图6(c) 3种字典间隔的情况，可以看出本文方法的估计性能在不同字典间隔情况下变化很小，而2维字典压缩感知方法和压缩感知结合3次相位变换方法的估计性能主要取决于字典间隔，当字典间隔增大时，上述两种对比方法的估计效果下降十分明显。因此可以证明，当目标速度参数没有落在预先设定的字典网格上时，对比方法都因字典失配而估计性能明显下降。而本文方法将字典失配误差作为参数进行贝叶斯学习，进而修正失配的字典，在3种字典间隔的情况下都能获得更接近CRB的估计性能，即目标速度参数没有落在预先设定的字典网格上时，本文方法仍能高精度估计目标速度参数。

图6 不同字典间隔时目标速度估计均方误差随信噪比变化情况

图7为不同字典间隔时目标加速度估计的结果。此时字典在4 0～60 m/s2范 围字典间隔分别取0.1 m/s2，0.2 m/s2和0.5 m/s2。可以看到与图6相似的结果，采用固定字典的两种对比方法在存在字典失配的情况时估计性能随字典间隔增大下降十分明显，而本文方法则在字典失配程度加重的情况下仍然能够保持稳定的估计性能。

图7 不同字典间隔时目标加速度估计均方误差随信噪比变化情况

5 结论

针对基于稀疏恢复的空时自适应处理目标参数估计方法中字典失配导致的估计性能下降问题，本文提出一种基于稀疏贝叶斯字典学习的高精度目标参数估计方法。实验证明，本方法能够有效提高字典失配情况下的目标参数估计精度，估计性能优于已有字典预先离散化的稀疏恢复空时目标参数估计方法。