基于有限新息率的非瞬时扩散点源参数估计方法

付 宁 沈孟垚 尉志良 乔立岩

(哈尔滨工业大学电子与信息工程学院 哈尔滨 150001)

1 引言

近些年来，随着无线传感器的发展[1，2]，利用无线传感网络进行物理场监测逐渐成为热门的研究方向。通常，这些物理场是由偏微分方程决定的，比如扩散场是由扩散方程驱动的。扩散方程是由德国物理学家Fick根据傅里叶的热传导方程在1855年提出的，描述了物质从高浓度区向低浓度区迁移规律，是2阶偏微分方程。对于扩散方程的求解问题，在数理领域得到了广泛的研究；而对于扩散源的估计问题，是在20世纪80年代才开始兴起。

扩散场不受带宽限制，因此想要用经典的带限重构框架实现参数恢复，则需要非常密集的样本。为了减小带宽的限制，对于扩散场重建问题，Van Waterschoot等人[3]用了有限元的方法进行场估计；此外，还有基于贝叶斯估计的统计估计技术[4]。直接恢复场的方法仍需要密集的采用网络才能可靠地恢复扩散场，于是有人通过将场源模型化，将恢复场的问题转换为场源的未知参数的估计问题。例如2011年，Ranieri等人[5]提出了一种基于压缩感知的方法；Rostami等人[6]又引进了扩展的压缩感知来解决这个问题。然而基于压缩感知的方案依赖于统一的空间采样，这在实践中往往难以实现。Zhang等人[7]针对传感器监控节点集中分布的问题，提出了一种基于K-Coverage的监控节点选择算法，有效提高了扩散源定位的准确性；而Alexandru等人[8]则采用移动的传感器进行采样，能对传感器的轨迹和扩散源位置进行估计；为了解决源个数未知的情况，Wang等人[9]提出了利用扩散场的峰谷结构来确定扩散源个数；除此之外，Flegg等人[10]提出了3维空间内的扩散衰减类型的点源的参数估计方法。因为这些方法中的一些没有对扩散源的时间性质做出假设，所以更普遍地适用，但是它们可能在噪声情况下变得不稳定，或者不能在空间和时间上重建整个场。

自2002年有限新息率(Finite Rate of Innovation， FRI)采样理论提出以来[11]，欠采样方法也越来越多地出现在人们视野里。FRI采样理论能以远低于奈奎斯特采样率的采样速率对信号进行采样，从而重构原始信号。2011年在FRI框架下，Dokmanic等人[12]对1维的瞬时点源进行了恢复；而在2011年，Lu等人[13]拓展了时间已知，位置未知情况下的2维多点源的定位方法；2012年，Ranieri等人[14]针对位置已知，时间未知的点源，时间是FRI信号类型的源进行了时间参数的恢复；帝国理工学院的Murray-Bruce[15]利用reciprocity gap原理提出了构造广义测量值对多个瞬时点源利用Prony-like方法进行恢复，其方法能进行多个瞬时点源的同时估计，并将其应用到时间衰减点源的情况[16]；随后，他们改变广义测量值的获取方法，利用广义Strange-Fix提出了新的恢复框架以解决物理驱动的场点源恢复问题[17]。然而上述方法都是针对点源信号恢复提出的，对于例如烟囱的化学物质排放，小孔泄露等问题，此时扩散源的发生时间与扩散场的监测时间相差不大，扩散源将不能被当作瞬时源，此时继续采用上述建模和参数估计方法将产生较大估计误差，甚至出现估计错误。特别地，对于非瞬时源，以上方法不具备估计扩散源持续时间的能力。综上，目前关于扩散源的参数估计方法都集中在扩散源类型为瞬时的狄拉克脉冲，而对于非瞬时的扩散场景这种方法不再适用。

本文的创新点主要在于：一是扩展了扩散源模型，通过脉宽可变脉冲(Variable Pulse Width， VPW)信号进行建模，能更好地对非瞬时类型的扩散源进行拟合，因为脉宽可变脉冲可看作狄拉克脉冲的泛化，所以本文提出的算法的适用范围更广；二是本文提出的算法能针对非瞬时类型源得到更准确的参数估计，相比其他方法，本文的方法利用估计得到的参数，能够更准确地重构出原始扩散源的时间函数，从而判断出扩散源的持续时间和幅度等参数。

本文在第2节介绍参数估计的问题模型；第3节描述扩散源模型基础VPW信号的FRI采样理论；第4节从扩散源建模，采样和信号重构几方面介绍文中提出的基于有限新息率的非瞬时的参数估计的算法实现；第5节通过仿真实验证明算法的有效性，同时探究估计结果精度的影响因素，并通过算法对比证明本文提出的算法对于非瞬时源的参数估计更加准确。

2 扩散源参数估计问题

扩散是一种物理现象，其描述了物质分子从高浓度区域向低浓度区域迁移，直至均匀分布的过程。扩散方程是一个2阶偏微分方程，其模拟了许多生物和物理现象，如流体中温度的变化、疾病流行动态和生物化学物质释放等。考虑扩散方程

3 脉宽可变信号的有限新息率采样理论

3.1 VPW信号

脉宽可变信号是非理想的FRI信号，其脉冲形状未知。单个脉宽可变脉冲由对称部分和反对称部分组成，其表达式为

3.2 VPW脉冲的参数恢复

3.3 指数再生核

4 扩散源参数估计算法

4.1 扩散模型

已知扩散源个数，传感器采样值和传感器的位置与采样时间信息，恢复扩散源的位置参数、脉宽、幅度和时延参数。具体过程可分为两大步骤：第一，根据对实际测量值进行加权组合得到广义测量值，利用指数再生近似理论，计算出组合系数；第二，对加权组合之后的测量值用多维谱估计算法恢复未知参数。

4.2 扩散源参数估计

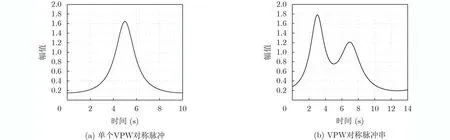
图1 VPW脉冲时域波形

首先对扩散场进行采样，在位置xn，时间tl的传感器采样值为φn(tl)。本文研究的非瞬时扩散点源的参数恢复框架分为两大部分：一是对实际测量值进行线性组合来近似广义测量值，二是根据广义测量值来估计位置参数、脉宽参数和幅度参数。

4.2.1 由广义测量值得到扩散源参数

综上，已知实际测量值，利用求得的组合系数，对其进行线性组合，近似得到广义测量值，利用谱估计算法分别求出位置参数、时间参数、脉宽参数和幅度参数。将上述参数估计过程总结成算法如表1：

表1 非理想时间脉冲扩散点源参数估计过程

5 仿真结果及分析

本节通过仿真实验来验证非理想脉冲的点源的参数恢复算法的准确性。首先用计算机模拟了一个2维空间的扩散场，即d=2，x=(x1，x2)。假设传感器是均匀放置的，且所有传感节点是同步的，用传感器网络对扩散场进行时间均匀采样，对得到的采样值用第4节所述算法进行扩散源参数的恢复。位置参数恢复结果如图2所示，图中绿色的点代表传感器，“*”代表估计的扩散源位置，“五角星”代表扩散源的真实位置。本次实验中，仿真模拟式(4)所示的扩散源形成的扩散场，根据表1提供的算法对扩散源参数进行估计。其中，参数设置参考文献[17]进行设置，采样总时长T=15 ，K1=K2=15 ， 采样时间间隔为1，S NR=30 dB。噪声是在模拟扩散场的采样基础上添加零均值的高斯白噪声，进行100次独立实验，采用3组不同的时间脉冲函数，时延、脉宽和幅度参数设置及估计结果的均值和方差如表2所示。其中，方差的计算公式为：

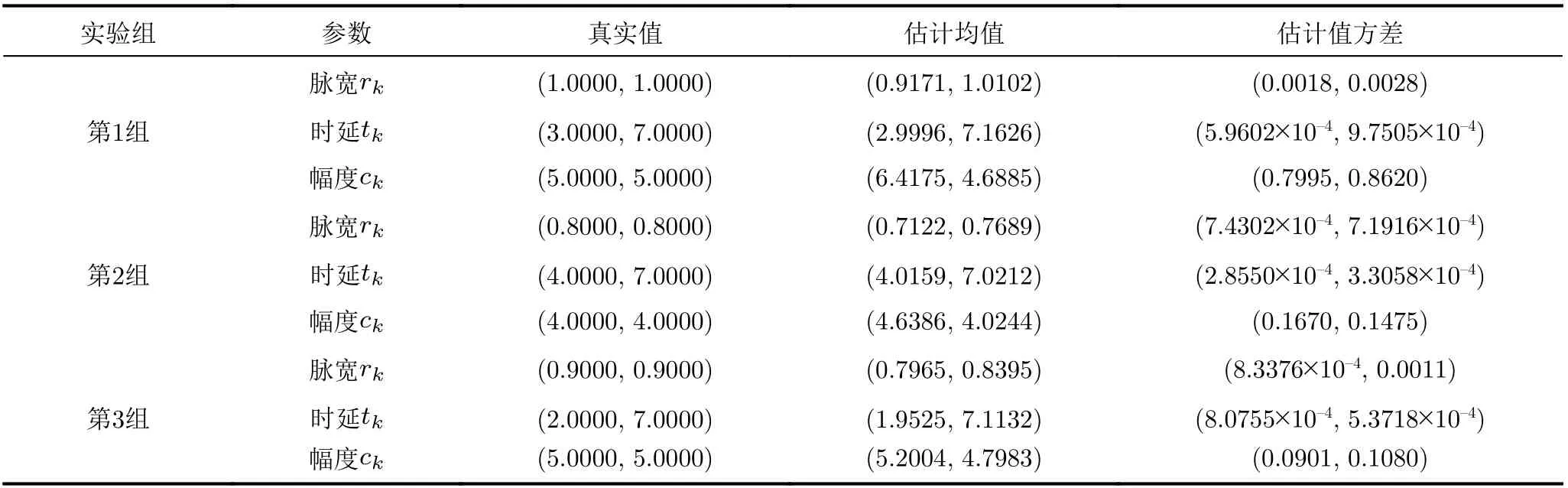
表2 参数设置及恢复结果

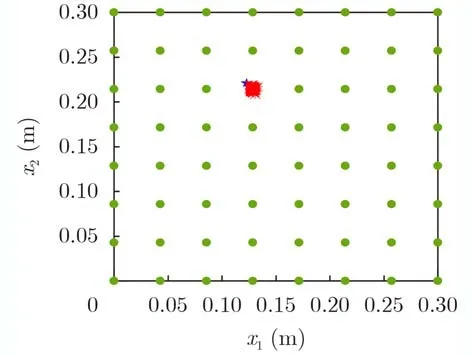
图2 位置恢复结果

根据上述结果，对于扩散源的位置、时间这些重要的参数，在有噪声的情况下，本文提出的算法也能进行近似的估计。估计结果会存在误差，因为在本文的算法中利用了指数再生近似原理，即格林函数不能严格满足Strang-Fix条件，在此意义下，得到的组合系数是逼近指数的系数，因此，即使是在无噪声的情况下，估计结果也不能完全与真实值相等，但是可以得到其近似值。

下面介绍了本文对于非瞬时扩散点源算法恢复的优越性。对于图5所示的扩散点源，当时间函数脉宽很小时，采用现有的瞬时点源模型和本文所提出的点源模型的参数恢复结果对比，SNR=30 dB，每种方法进行100次独立实验，采用两组不同的参数设置，参数估计结果的均值和方差如表3所示。

对于图5所示的扩散源的恢复，本文的时延和幅值的估计结果是在得到VPW对称脉冲参数的基础上计算而来的，由表3可以看出本文提出算法的参数估计比瞬时点源模型的参数估计结果更接近真实值，对于幅值的估计的方差也更小，虽然时延估计的方差比瞬时点源估计方法稍大，但是因为瞬时点源估计的时延均值与真实值相差较大。为了更进一步说明两种模型的恢复结果，图6展示了在不同信噪比下的参数估计误差，每个SNR下进行100次独立实验。

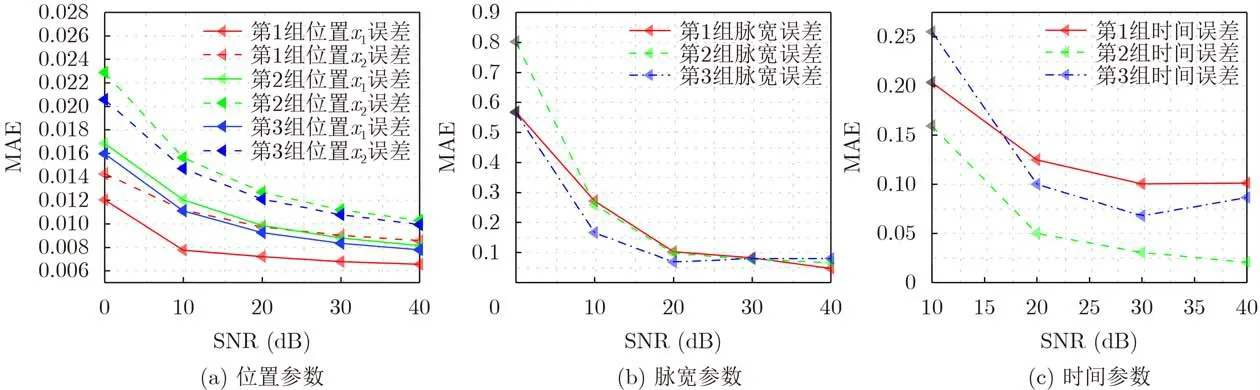
图3 MAE与SNR的变化关系

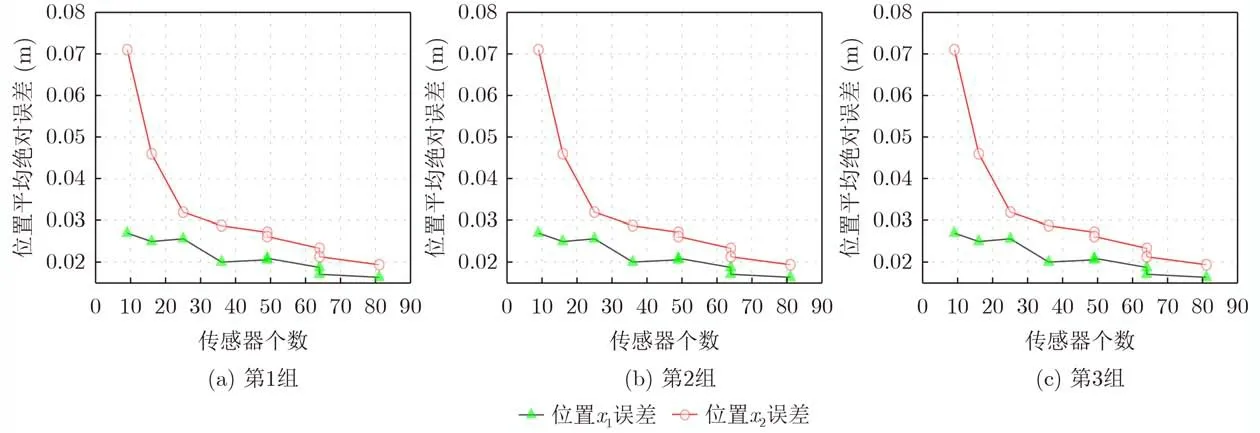
图4 传感器密度与参数恢复误差

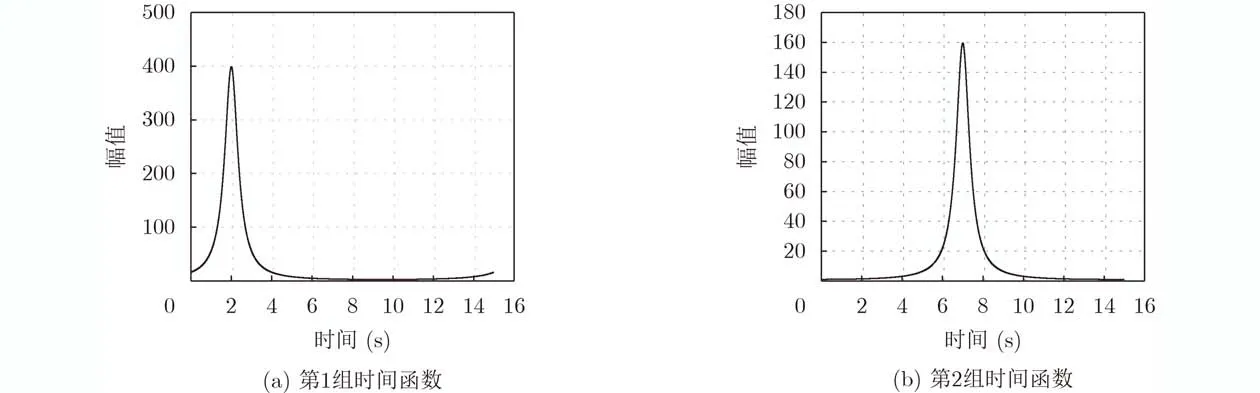
图5 非瞬时时间函数

表3 参数估计结果

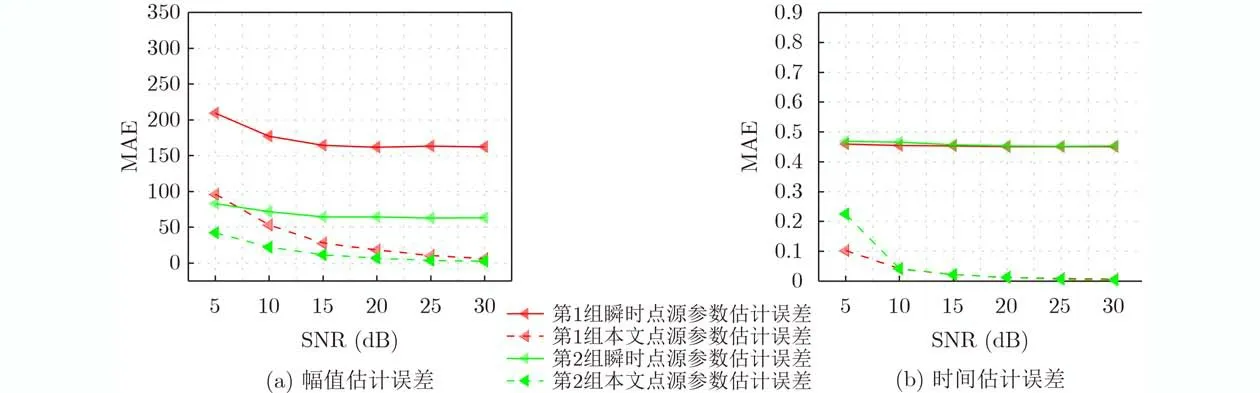
图6 瞬时点源模型与本文点源模型恢复误差对比

通过图6可以看出，本文提出的点源模型的参数估计误差比瞬时点源模型的参数估计误差更小，同时随着噪声水平的减小，本文的非瞬时模型的参数估计误差减小得更多。综上，本文提出的非瞬时点源的参数估计算法对于图5所示的恢复效果比瞬时点源模型的恢复效果更好，因为本文提出的非瞬时点源模型与图5所示非瞬时扩散源类型更加匹配。

6 结束语

本文针对非理想时间脉冲的扩散点源，在瞬时点源的研究基础了提出了改进的基于有限新息率的非瞬时扩散点源的参数恢复算法。对于不能认为是瞬时发生的扩散源，其发生时间相对于测量时长不能忽略，本算法利用无线传感器对扩散场进行采样，对采样值进行线性组合，组合系数利用指数再生近似理论获得，对组合后的测量值利用FRI理论中常用的恢复算法––谱估计方法进行扩散源的参数估计，对于非理想时间的扩散点源，本文提出的参数估计方法比瞬时点源模型更加准确，仿真结果验证了此种方法的有效性和准确性。