支持终端晃动的多光源可见光通信系统有效容量研究
钱 磊 刘飞扬 赵琳琳 戈立军* 迟学芬
①(天津工业大学电子与信息工程学院 天津 300387)
②(天津市光电检测技术与系统重点实验室 天津 300387)
③(吉林大学通信工程学院 长春 130012)
④(伦敦大学学院计算机科学学院 伦敦 WC1E 6BT)
1 引言
新一代网络中大量新型业务涌现,对网络的时延服务质量(Quality of Service, QoS)保障提出了较高的要求[1]。无线时延QoS保障需要以牺牲带宽为代价,在无线频谱资源短缺的现状下,时延QoS保障越来越困难。为缓解无线频谱资源短缺与通信业务量增长及时延QoS保障之间的矛盾,下一代网络亟需拓展新型频谱资源。近年来,占用400~800 THz免授权频段的可见光通信(Visible Light Communication, VLC)以其超高的传输速率有望为下一代网络提供更严格的时延QoS保障,成为国内外学术界、工业界关注的热点[2]。
相较于电磁波,可见光的直射性较强,且相比于射频信道,VLC信道并非各向同性[3]。因此,VLC易受终端晃动的影响。在实际VLC系统中,智能终端在接收VLC信号的过程中,并非始终保持垂直向上,智能终端的方向常因用户姿势的变化而发生改变,即发生终端晃动。在现有VLC的研究中,大多未考虑终端晃动对VLC传输的影响。然而,事实上,终端晃动将导致VLC接收平面方向的变化,进而对接收端入射角、VLC信道增益与传输速率产生较大的影响。
2016年,文献[4]提出可以基于航向角、俯仰角和横滚角描述终端在3自由度的随机晃动,并首次分析了终端随机晃动对吞吐量和网络负载均衡的影响。文献[5]研究了终端晃动对VLC视距链路(Line of Sight, LoS)信道增益的影响,并提出了信道增益的统计分布模型。文献[6]探索了终端晃动角度对VLC信道容量的影响,从信息论的角度推导了VLC容量上、下界,并以VLC容量下界最大化为目标求解了终端的最佳晃动角度。同年,文献[7]以开关键控调制下独立噪声VLC系统的误码率(Bit Error Ratio,BER)最小化为目标求解了终端的最佳晃动角度。尽管文献[2–7]从不同角度分析、优化了终端晃动对VLC系统性能的影响,但上述研究中对终端晃动的随机性均存在假设,并未从实际出发建模终端的随机晃动过程。2019年,文献[8]采用智能终端配备的陀螺仪、加速器和指南针,对40个测试者在静止场景和匀速固定路径移动场景中使用VLC终端的晃动过程进行采样,并通过对实测数据的拟合分析,提出了VLC系统统计晃动模型。研究结果表明,静止用户和移动用户的晃动方位角均服从均匀分布,且其晃动极化角分别服从截断式拉普拉斯分布与截断式高斯分布。在该结论的基础上,文献[9]分析了终端随机晃动对VLC系统BER和SNR的影响。文献[10]分析了终端随机晃动对VLC系统物理层安全容量和安全中断概率的影响。进一步地,2021年,文献[11]综合用户的随机空间分布与随机晃动,提出VLC信道增益的统计模型,并分析了VLC系统的BER性能。目前为止,现有研究均未考虑终端晃动对VLC系统时延QoS的影响。
近年来,考虑到无线信道的随机性使得传统确定性时延QoS分析方法难以适用,以大偏差理论为基础的有效容量理论逐渐成为建模分析无线通信统计时延QoS的主要方法[12]。有效容量的物理含义是指对于某一给定的服务过程,在满足排队时延要求的前提下,系统可支持的最大到达速率[13]。在VLC系统中,信道遮挡、用户移动、终端晃动等因素也使得VLC信道具有较强的随机性,因此,部分学者考虑基于有效容量分析VLC系统的时延QoS,研究VLC系统中统计时延QoS约束下可达传输速率。文献[14]和文献[15]将有效容量理论应用于VLC和射频异构网络,分析因VLC信道遮挡导致的服务过程随机性对统计时延QoS的影响,并分别提出异构网络终端资源分配与链路选择算法。在此基础上,文献[16]针对统计时延QoS约束下以用户为中心的VLC组网问题展开研究。此外,针对上行多用户VLC网络,文献[17]综合随机接入与信道遮挡建模VLC系统的随机服务过程,提出支持终端统计时延QoS保障的接入算法。文献[18]研究了私密VLC场景下,终端的差异化统计时延QoS保障问题。现有VLC系统时延QoS方面研究均假设终端方向始终为垂直向上,未考虑终端晃动对VLC系统时延QoS分析与保障的影响。
在实际VLC系统中,终端的随机晃动将对VLC信道增益与传输速率产生影响,从而使VLC系统的服务过程具有时间相关性。现有研究均未从时间相关性的角度出发对VLC终端随机晃动进行建模,也未分析随机晃动对终端统计时延QoS的影响。鉴于此,本文在考虑终端随机晃动的影响因素下,基于有效容量理论,研究具有统计时延QoS约束的VLC终端的传输速率。具体贡献如下:
(1) 本文基于3维离散时间马尔可夫链为VLC终端构建了3自由度随机晃动模型,利用晃动过程中航向角、俯仰角、横滚角的变化,从时间相关性的角度刻画了VLC终端的随机晃动过程。
(2) 基于有效容量理论,本文提出了支持终端晃动的多光源VLC系统有效容量,用于表征终端随机晃动的影响因素下,具有统计时延QoS约束的VLC终端的传输速率。
(3) 仿真结果说明了终端晃动对多光源VLC系统容量的影响,验证了本文所推导有效容量的准确性,并分析了不同晃动模型参数、不同系统参数对晃动终端有效容量的影响。
2 系统描述
2.1 VLC信道
在如图1所示的室内下行多光源VLC系统中,共有NU个终端(User Equipment, UE),NA个接入点(Access Point, AP)。AP与UE间采用矢量传输方式[16]。UE接收到的信号包含来自LoS链路的直射光信号与来自非视距链路(None Line of Sight, NLoS)的反射光信号。由于LoS链路是VLC的主要组成部分,LoS链路比NLoS链路中最强的部分还高出7 dB[19]。因此,本文只考虑LoS链路。

图1 室内下行VLC系统
根据文献[19],第i个AP与第j个终端之间的LoS链路增益可表示为



2.2 终端晃动描述
在实际室内VLC场景中,用户持有的终端设备会随着用户使用姿态的不同而随机晃动,终端的接收平面法向量并非始终垂直向上。考虑到目前大多数智能终端均配备有陀螺仪、加速器和指南针,当终端随机晃动时,其可在3个自由度上测量终端的晃动情况。为建模终端的随机晃动,本文以终端的接收点为原点建立3维笛卡儿坐标系,分别通过航向角α、俯仰角β和横滚角γ描述终端在3自由度的随机晃动,如图2所示。具体来说,航向角α描述了终端围绕Z轴的旋转,α取值范围是0°到360°;俯仰角β描述了终端围绕X轴的旋转,取值范围是–180°~180°;横滚角γ描述了终端围绕Y轴的旋转,取值范围是–90°到90°。
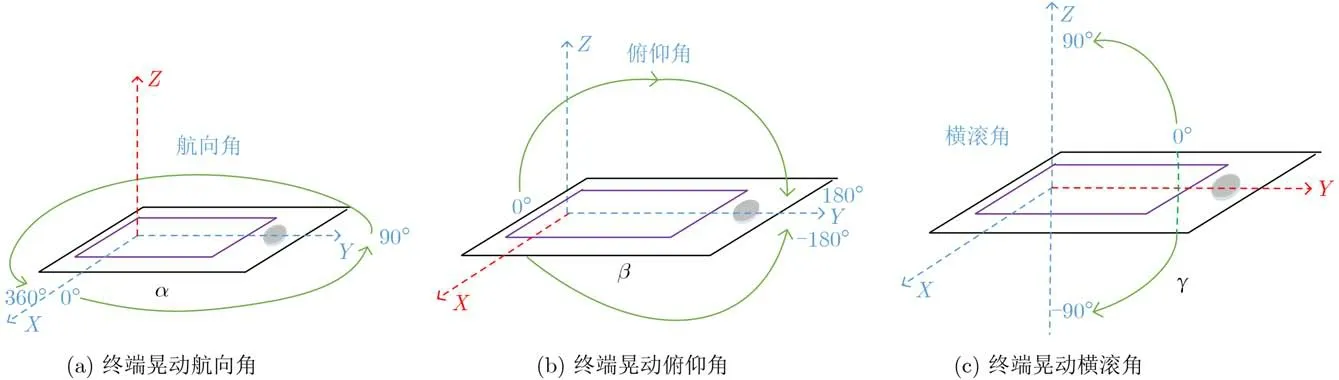
图2 3自由度终端晃动示意图

2.3 有效容量
为描述统计时延QoS约束对VLC的影响,本文采用有效容量刻画终端晃动场景下VLC的传输速率。在基于排队论建模的VLC系统中,终端j的缓存被视为一个具有随机到达过程的队列,该队列的服务过程即为VLC系统的传输过程。终端j的统计时延QoS要求由时延界(最大容忍时延)和时延界违反概率共同刻画,即

3 支持终端晃动的VLC系统有效容量
3.1 基于3维离散时间马尔可夫链的VLC终端晃动模型
在室内VLC系统中,终端的晃动常由用户的姿势变化引起,具有随机性。考虑到用户动作的连续性,晃动前后的终端接收平面方向的变化往往具有相关性,换言之,晃动终端在某时刻的接收平面方向与上一时刻的方向有关,而与之前时刻的方向无关。因此,终端的晃动过程可视为具有突发性、时间相关性的随机过程。
鉴于马尔可夫过程具有无记忆性,本文基于3维离散时间马尔可夫链构建终端晃动模型。为刻画终端的3自由度随机晃动,本文以终端的晃动角度(α,β,γ)定义马尔可夫链的状态,并假设在两次连续对终端晃动状态的观测采样中,终端只能在航向角α、俯仰角β、横滚角γ的任意一个角度发生变化,进而跳转至下一个状态。本文假设终端的晃动角度变化步长分别为 Δα,Δβ,Δγ。基于3维离散时间马尔可夫链的终端晃动模型状态转移情况如图3所示,其中P00与Pkl,k=1,2,3,l=1,2分别表示马尔可夫链的状态逗留概率与转移概率。根据马尔可夫链的性质,可得

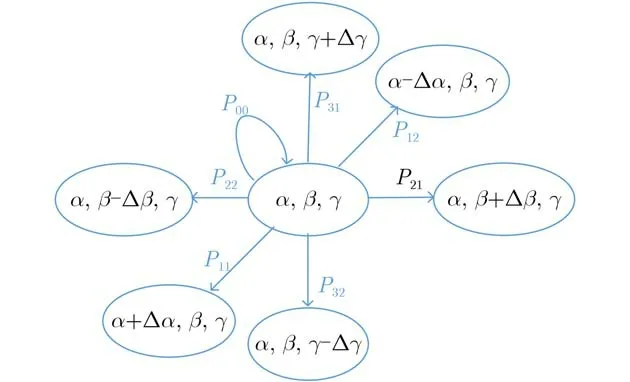
图3 3维离散时间马尔可夫链的状态转移情况



假设Vm为如图4所示的状态空间中的某状态,其下一个跳转状态为Vn,则根据晃动终端在3自由度的角度变化范围及不同晃动状态的转移情况,可将马尔可夫链状态转移概率矩阵Q表示为
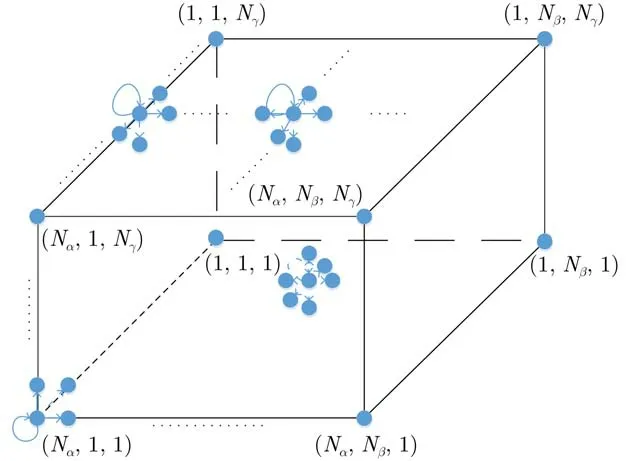
图4 3维离散时间马尔可夫链的状态空间

其中,由于状态转移概率矩阵Q是维度为(Nα×Nβ×Nγ)×(Nα×Nβ×Nγ)的方阵,因此(m,n)∈{(m,n)|1≤m≤Nα×Nβ×Nγ, 1≤n≤Nα×Nβ×Nγ}。
3.2 基于矢量传输的晃动VLC终端系统容量

在如图1所示的室内下行VLC系统中,当终端的晃动状态为Vm时,基于矢量传输的VLC系统容量为其中,d(i,j)为从APi到UEj的LoS链路方向矢量,n′m表示终端的晃动状态Vm对应的接收平面法向量,n′m与 航向角α、 俯仰角β、横滚角γ的关系如式(6)所示。
3.3 支持终端晃动的VLC系统有效容量
本文基于3维离散时间马尔可夫晃动模型,将VLC系统对晃动终端的服务过程视为离散时间马尔可夫随机服务过程。在该服务过程中,马尔可夫状态Vm ∈{1,...,Nα×Nβ×Nγ}所 对应的服务速率为Cm,如式(11)所示。在排队系统服务间隔Ts内,处于状态Vm的 终端被服务的比特数为Λm=TsCm。根据马尔可夫晃动模型中终端晃动状态的跳转规律,随机服务过程中被服务比特数的变化情况遵循状态转移概率矩阵Q,该矩阵为不可约的非周期状态概率转移矩阵,如式(10)所示。
根据文献[20],利用后向方程与Perron-Frobenius定理,可将马尔可夫随机过程的对数矩生成函数推导为

4 仿真结果分析
本文考虑房间尺寸为5×5×3 m3多光源VLC系统。VLC系统内共9个AP,且以3×3矩阵方式均匀部署于房间天花板上;共3个终端,随机分布于房间内。主要仿真参数如表1所示。

表1 VLC系统仿真参数

图6展示了VLC系统的有效容量随终端的统计时延QoS指数的变化情况,其中P00=0.2,视场角为45°,角度量化步长为30°。有效容量理论值的计算方式如式(14)所示,有效容量仿真值的获取方法参见文献[13]。从图6可以看出,系统有效容量的仿真值与理论值差距较小,体现了在支持终端晃动的VLC系统中,本文对基于3维离散时间马尔可夫链晃动模型的有效容量建模的准确性。由于较高的QoS指数对应较严格统计时延QoS约束,且较严格统计时延QoS约束下的VLC系统可达传输速率较小,因此,在图6中,VLC系统有效容量随终端统计时延QoS指数的增加而减小。换言之,VLC系统的统计时延QoS要求越严格,通信系统在保障该QoS的前提下能够支持的最大稳定的数据包到达速率就越小。为对比不同晃动模型下的有效容量差异性,本文将基于文献[8]中晃动模型所计算的有效容量作为对比值。从图6子图中可以看出,有效容量对比值仍保持着随QoS指数增加而减小的趋势,但其随QoS指数的变化较为缓慢。其原因在于:文献[8]从晃动极化角统计分布的角度构建了晃动模型,而本文从时间相关性的角度刻画了终端的随机晃动过程。在基于排队论的统计时延QoS分析框架中,服务过程的时间相关性可视为有效容量的决定性因素之一。因此,在考虑时间相关性的晃动模型下,终端的有效容量对QoS指数的变化更加敏感。
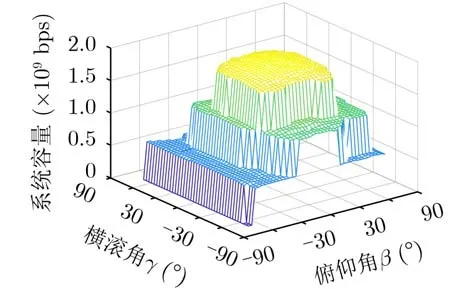
图5 终端晃动对多光源VLC系统容量的影响
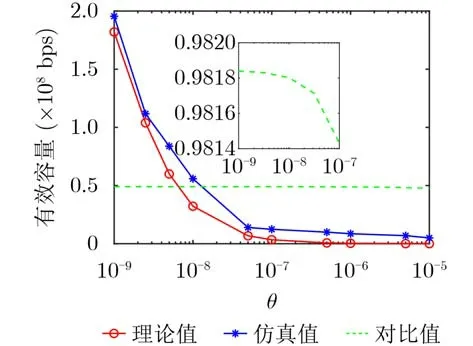
图6 VLC系统有效容量的理论值与仿真值对比
图7展示了多光源VLC系统有效容量随终端视场角的变化趋势,其中P00=0.2,终端的统计时延QoS指数为10–8。从图7可以看出,在本文所提出的3维离散时间马尔可夫链晃动模型中,当相邻两个马尔可夫链状态之间的晃动角度量化步长固定时,增大视场角有助于为接收端增加接收光链路的机会,因此可以显著提高VLC系统有效容量。此外,当终端视场角固定时,提高晃动模型中3个晃动角度的量化步长,VLC系统有效容量将会减小。其原因在于当晃动角度量化步长减小时,晃动后VLC信道质量差的终端(例如,终端晃动后,接收平面方向朝向房间的边缘或角落)将有更多的机会被采样,从而导致VLC系统有效容量降低。
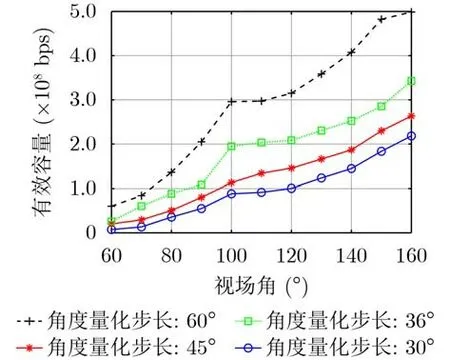
图7 VLC系统有效容量随视场角变化
5 结束语
本文针对实际VLC系统中,终端随机晃动对统计时延QoS约束下的VLC系统传输速率的影响展开研究。考虑到随机晃动所带来的时间相关性是影响统计时延QoS分析的关键因素,本文基于3维离散时间马尔可夫链建模VLC终端的3自由度晃动过程。在此基础上,基于有效容量理论,推导晃动终端在统计时延QoS约束下的可达传输速率,并通过仿真验证了所推导有效容量的准确性及晃动模型参数、终端视场角等对晃动终端有效容量的影响。在本文研究的基础上,未来将继续探索在保障用户统计时延QoS要求的前提下,终端晃动对VLC系统组网、切换等性能的影响。

