一种高效的点云去噪聚类方法
钟文彬,肖振远,刘光帅
(1.中国电子科技集团公司第十研究所,四川 成都 610036;2.西南交通大学机械工程学院,四川 成都 610031)
1 引言
在逆向工程中,使用激光扫描设备获取点云数据时,由于受到操作设备的精度、操作人员的经验、环境因素、物体表面特性等影响,使得采集得到的点云数据会引入与目标点云无关的噪声点云,这些噪声点云严重影响后期的处理,如特征提取、特征匹配、三维重建的精度等[1-3]。因此,对获取的包含噪声的点云数据进行预处理显得至关重要。
近年来,研究者针对点云的预处理进行了大量的研究[4-9]。文献[4]提出基于方法库的点云去噪方法,利用统计滤波结合半径滤波可以去除大尺度噪声,但对于距离目标点云类较近的噪声点,该方法无法有效去噪。文献[5]提出拟合二次曲面实现点云的去噪,该方法依赖于鲁棒的法向估计和基于投影的局部曲率,可很好的保持特征,但法向估计易受偏差的干扰。文献[6]提出基于特征选择的双边滤波点云去噪算法,该方法较好的保留了点云的细节特征,当存在大尺度噪声时,双边滤波会产生过光顺的问题,因此不适合对离群点云噪声滤波。文献[9]用K-means聚类算法对点云进行聚类,根据点到聚类中心的欧式距离和临近点曲率变化判断每个类中的点是否为噪声点,去除外部噪声点云,由于Kmeans聚类算法对初始值较敏感,因此去噪效果难以把控。
以上滤波算法在点云去噪时不能较好的将离体噪声点云去除,严重影响后期点云三维重建的精度。针对上述问题,在密度聚类点云去噪算法基础之上,提出一种高效的点云去噪聚类方法。该方法摒弃密度聚类算法使用欧氏距离逐点遍历判断的思想,采用KD-tree[10]对点云数据进行搜寻,将点云数据按某一维度进行排序,在确定的核心点云邻域外选择未标记的最近点云进行扩展密度类,最后分离出点云数量最大的点云类以完成点云去噪。
2 方法框架
该方法以手持激光扫描仪获取的有序点云为对象,提出一种高效的点云去噪聚类算法。算法去噪的整体框架流程,如图1所示。首先,对原始点云建立KD-tree空间索引结构;接着,选择点云的某一维度,找出该维度最小索引核心点云;然后,沿该维度方向按方法提出的聚类方法扩展密度类;最后,分离最大点云数量的密度类,得到目标点云。

图1 文章方法框架Fig.1 The Framework of this Paper
3 高效的点云去噪聚类方法
对获得的点云数据分析可知,原始的点云数据分布存在一定的规律,即目标点云中相邻两个点的间距保持在激光扫描设备设定的采样间距范围之内上下波动,连续布满整个空间位置。而噪声点云是随机误差造成的,其相邻点之间的间距不确定、位置不固定。密度聚类是一种无监督聚类算法,能在“噪声”数据中识别出任意形状的聚类[11-15],在点云应用邻域较其他聚类算法有着独特的优势。但由于密度聚类在去除点云噪声时需要对点云进行逐个遍历,利用欧式距离进行邻域点判断,内存要求较高,收敛时间较长,降低了点云去噪的效率,不适合海量点云的去噪处理。为克服以上密度聚类去除点云噪声时的缺点,提出一种高效的点云去噪聚类方法。
3.1 KD-tree建立空间索引
密度聚类算法点云去噪时使用欧氏距离逐点遍历的思想。因此,为加快点云查找的速度,该方法采用KD-tree空间索引结构。KD-tree是一种k维数据结构,能快速搜寻近邻点。该结构选择点云的某一维度,以该维度的中位数将数据分为两部分,然后对其他维度重复该过程,直至将点云数目分割成单个点。点云KD-tree结构(为便于描述,所有点云描述图均为二维表示),点a和点g是以半径为r、邻域点数为3确定的核心点云,如图2所示。

图2 点云KD-tree结构Fig.2 The Structure of Point Cloud KD-tree
3.2 点云去噪聚类方法
获取的点云数据大多数为几十万量级点云,对于较大的精密的对象,获取的点云数量为百万级至千万级点云,使用密度聚类需要对逐个点云遍历判断,需要根据设定的ε和m遍历计算每个点云数据,其时间复杂度为是O(N*找出ε邻域中的点所需要的时间),N为点云的个数,最坏的情况下时间复杂度可能是O(N2),降低了点云噪声的效率且对内存要求较高。该方法在去除噪声点时,由于加入KD-tree进行索引,可以将复杂度降到O(NlogN)。通过点云分析发现:若点云中某个点为核心点云,则该点邻域内所有点与该点属于同一类,则下一点选择的对象不应在该点确定的邻域内,从该点邻域外选择下一点,从而可以大量降低了点云遍历的次数,其查询点的个数小于N,故时间的复杂度小于O(NlogN),从而提高了点云去噪的效率。该方法在点云去噪时涉及以下相关概念:
概念1 直接密度可达(Directly Density-Reachable)
给定一片点云D,点q是一个核心点云,点p是在以点q为球心、ε为球半径的邻域内,则称对象p从对象q出发是直接密度可达的。如图2所示,其为点云数据的一部分,点a是以球的半径为r、邻域点云数量为m= 3确定的核心点云,其邻域内的所有点云均为从点a出发是直接密度可达的。
概念2 密度可达(Density-Reachable)
如果存在一个点云对象链p1,p2,p3,...,pn,p1=q,pn=p,对pi∈D(1 ≤i≤n),pi+1是从pi关于ε和m直接密度可达的,则对象p是从对象q关于ε和m密度可达的,如图3(a)所示,p到q是密度可达的。

图3 点云数据描述Fig.3 Point Cloud Data Description
概念3 密度相连(Density Connection)
如果点云D中存在一个对象o,存在对象p和q均是从对象o关于ε和m密度可达的,那么称对象p和q是关于ε和m密度相连,如图3(b)所示,o为核心点云,p和q由于距离点云边界较近,未构成核心点云,但构成密度相连。
该方法的基本思想为:采用KD-tree对点云数据建立空间索引结构,将点云数据按某一维度进行排序,从排序最小的索引号确定核心点云,如果为核心点云,将邻域内的点与之归为同类。接着从排序的点云中选取距离上一核心点云最近的邻域外未标记的点云,判断是否为核心点云,如果为核心点云,且与上一核心点云的邻域有重叠点且重叠点存在核心点云,则将该核心点云及其邻域点与上一核心点云归为同类,否则为新类。如图4(a)所示,设定的球半径为ε和m= 6,p和q为核心点云,其邻域的重叠区域内存在点o是核心点云,故p、q及其邻域点云均为同类点云;如图4(b)所示,p和q为核心点云,其邻域的重叠区域o不是核心点云,故p和q为两类点云。依次遍历整个点云进行密度相连,最后分离点云数量最大的点云类以完成点云去噪。
图3中第一个峰为气体产物CO2,其相对含量最高(64.97%),CO2主要是由于羧酸类物质中羧基的断裂以及醛酸等物质的一次裂解产生。其后出现的色谱峰峰形较为复杂,主要为各种异构体。

图4 点云数据说明Fig.4 Point Cloud Data Explanation
3.3 方法步骤
该方法整体实现过程步骤如下:(1)根据激光扫描仪设定的采样间距选择方法所需的邻域半径和邻域点云个数;(2)对点云使用KD-tree建立空间索引结构;(3)选择某一维度对点云进行排序;(4)从最小索引点判断是否为核心点云,如果为核心点云,从核心点云邻域外选择最近点扩展密度相连,具体过程流程图,如图5所示;(5)统计各类点云的数量,提取最大数量点云,完成去噪。
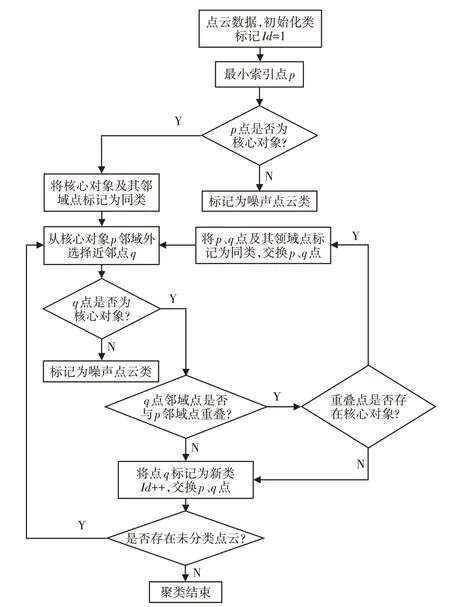
图5 聚类流程图Fig.5 The Chart of Clustering Flow
4 实验结果与分析
4.1 实验数据
文中使用天远设备的Freescan X5手持激光扫描设备获取的电路板的有序点云数据作为实验样本,如图6、图7所示。点云的格式为asc。截取局部右上角和局部右下角细节特征进行实验对比观察,原始点云中矩形、圆形、三角形标记处的噪声点云很明显。图中的黑色圆块为扫描时加入的标志点,左下方散乱区域是夹具夹持造成,忽略不计。使用C++程序语言在VS2015平台上扩展点云PCL模块实现算法,计算机配置为Intel(R)Core(TM)i5-9400F CPU@2.9 GHz、内存为16 GB、64 位的Windows10 操作系统、GTX1060显卡。

图6 右上角原始点云数据Fig.6 Raw Point Cloud Data in the Upper Right Corner
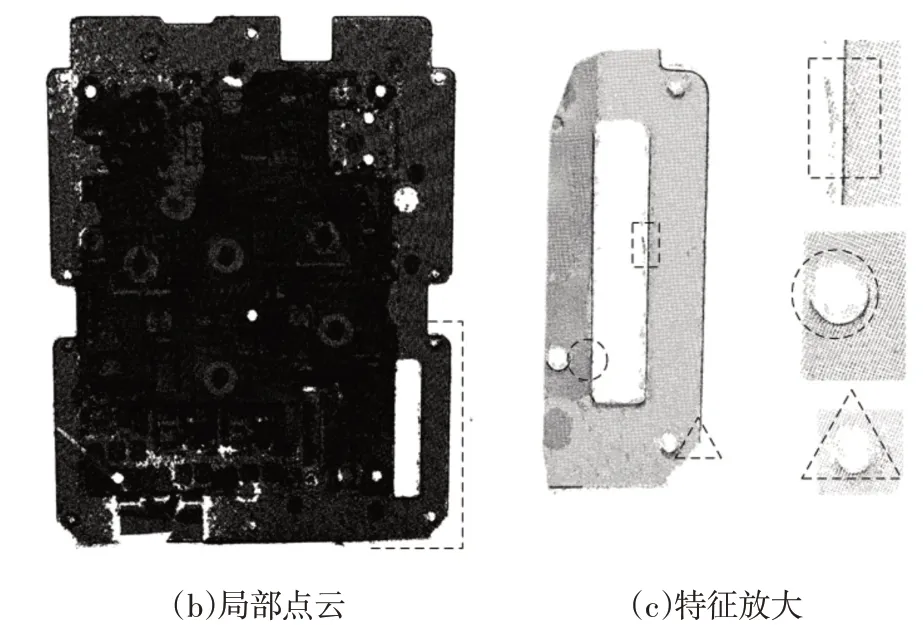
图7 右下角原始点云数据Fig.7 Raw Point Cloud Data in the lower Right Corner
4.2 去噪对比实验与分析
将本方法与主流点云库中的统计滤波、半径滤波和密度聚类去噪算法进行对比实验结果,如图8、图9所示。相关数据,如表1、表2所示。实验所取参数是经多次试验后,尽可能去除离体噪声点取得的最好效果对应的参数值,统计滤波标准差乘数为0.3,查询的近邻点数为300;半径滤波采用半径为0.0003m,半径内的近邻点数为8;密度聚类和本方法均采用半径为0.0003m,半径内的近邻点数为8。从图8和图9中可以看出:(1)图8(a)的三角形标注处和图9(a)的矩形标记处仍存在离体聚集的噪声点,图8(a)的圆形标记处内圆的轮廓被模糊,图9(a)的圆形标记处的特征圆衔接处被断开,原因是统计滤波在处理点云数据时,对每个点的邻域进行统计分析建立高斯分布,将距离处于标准差倍数范围之外的点判定为噪声点云去除,而目标点云体外的聚集的噪声点云也存在此种性质,故不能将体外聚集的噪声点完全去除,另外,当边界点云较少时,边界被模糊,如图8(a)右上角的边缘轮廓和图9(a)的三角形标注的右下角斜边轮廓;(2)图8(b)和图9(b)中的完整平面被稀疏模糊出现孔洞,原因是半径滤波将稀疏部分的目标点云当成噪声点云;(3)标记处的噪声点云经密度聚类算法和本方法处理后的效果如图8(c)和图8(d),不存在前述统计滤波和半径滤波问题,明显优于统计滤波和半径滤波。

图8 右上角去噪算法对比图Fig.8 Denoising Algorithm Comparison Diagram in Upper Right Corner

图9 右下角去噪算法对比图Fig.9 Denoising Algorithm Comparison Diagram in Lower Right Corner

表1 右上角去噪算法对比Tab.1 Comparison of Denoising Algorithms in the Upper Right Corner

表2 右下角去噪算法对比Tab.2 Comparison of Denoising Algorithms in the Lower Right Corner
从表1、表2中可以看出:
(1)统计滤波和半径滤波速度较快,去除了大量的点云,但其存在缺陷,如图8(a)和图8(b)的三角形标记和图9(b)中的矩形标记仍然存在离体噪声点云;
(3)本方法的速度明显快于密度聚类算法,仅次于半径滤波。这是由于本方法在去噪时,加入KD-tree进行索引,从邻域外进行遍历,依据重叠点判断密度相连,提高了聚类的速度。
5 结论
针对点云数据在曲率较大处及边界存在较多的噪声问题,提出一种高效的点云去噪聚类方法。通过对点云数据建立KD-tree空间索引结构,将点云按某一维度,从核心点云邻域外选择最近的未标记的样本点扩展密度类,最后分离出密度相连最大的目标点云类。实验针对手持激光扫描设备获取的电路板点云数据,对统计滤波、半径滤波、密度聚类和本方法去噪结果进行了对比,结果表明本方法能在去除孤立的或聚集的离体噪声点的同时可以较完整地保留目标点云,降低了对内存的依赖性,提高了点云去噪的质量。

