Iris Segmentation Based on Matting
CHEN Qiru, WANG Qi, SUN Ting, WANG Ziyuan
(1. Northeastern University, No. 3-11, Wenhua Road, Heping District, Shenyang, China;2. Tencent, Tencent Binhai Building, No. 33, Haitian Second Road, Nanshan District, Shenzhen, China)
Abstract: In this paper, we aim to propose a novel and effective iris segmentation method that is robust to uneven light intensity and different kinds of noises such as occlusion by light spots, eyelashes, eyelids, spectacle-frame, etc. Unlike previous methods, the proposed method makes full use of gray intensities of the iris image.Inspired by the matting algorithm, a premier assumption is made that the foreground and background images of the iris image are both locally smooth. According to the RST algorithm, trimaps are built to provide priori information. Under the assumption and priori, the optimal alpha matte can be obtained by least square loss function.A series of effective post processing methods are applied to the alpha image to obtain a more precise iris segmentation. The experiment on CASIA-iris-thousand database shows that the proposed method achieves a much better performance than conventional methods. Our experimental results achieve 20.5% and 26.4%, more than the well-known integro-differential operator and edge detection combined with Hough transform on iris segmentation rate respectively. The stability and validity of the proposed method is further demonstrated through the complementary experiments on the challenging iris images.
Keywords: Iris Segmentation, Trimap, Image Processing
1 Introduction
As an efficient biometric technology, iris recognition is a popular research topic in both academic research and industrial applications, and is widely used in personal identification[1-3]. Iris segmentation is the basic and significant step of iris recognition. However, several defaults in the segmentation process present problematic traits. For instance, irises are easily occluded by eyelids and eyelashes and are covered with specular reflections when persons wear thick glasses. Other difficulties in iris segmentation include de-focusing, over or under exposure, uneven illumination, and so on. Therefore, real applications are calling for more accurate and robust iris segmentation algorithms.
In response to the drawback that conventional iris segmentation methods are mostly sensitive to different kinds of noises, this paper, inspired by natural image matting algorithm, presents a novel iris segmentation method based on natural image matting algorithm. In summary, the key contributions of this work are as follow:
i) Our method makes full use of gray intensities based on the assumption of local smoothness, completely different from most previous methods’ sole dependence on the gray gradients. For one thing, the gradients of noises may disturb the iris boundary gradient. For another, the gradient information is not abundant enough when the iris is fully covered by eyelid.To tackle these downsides, the proposed method extracts alpha matte of iris image based on gray intensities. The novel matting-based iris segmentation method provides an avant-garde insight widely applicable for the iris segmentation field. In addition, different from the gen-eral interactive matting, the priori information is given automatically based on RST algorithm.
ii) The proposed method is robust to the noise iris images collected in the less-constrained environment.We use ellipse rather than circle to fit the pupillary boundaries because of the existence of iris images with off-axis view angle. According to the assumption that foreground and background images of iris image are both locally smooth, we deal with iris images in a small window around a pixel in order to obtain uniform illumination.
Our method is further verified on the iris images with uneven illumination, excessive and insufficient exposure, all have shown promising experimental results which proves its stability and validity.
2 Related Work
Daugman proposed the most well-known iris segmentation algorithm in [4], which is integro-differential operator. In general, the gray scales of pupil, iris and the sclera of an eye are gradually increasing along the radial direction. According to this obversion, a circle detection template is designed to locate the iris boundary. The basic idea is to find the position with the largest variation along the radial integral of the points on the circumference as can be seen in Equation 1.

Another well-known method is proposed by Wilds, which is edge detection combined with Hough transform[2]. This method use edge detection operator to procure the edge information of iris, pupil and sclera and the image is mapped into a binary image. According to the assumption that inner and outer boundaries are circular, Hough transform voting mechanism is used to detect the parameters of inner and outer circles. At present, integro-differential operator method and edge detection combined with Hough transform method are still the mainstream study of iris localization. Most of iris localization algorithms[5-8]are built on these two methods.
Integro-differential operator, edge detection combined with Hough transform method and the corresponding expansion methods displayed a relatively positive performance when dealing with ideal iris images. In practice, however, iris images are often collected in a less-constrained environment. In the presence of noises, the traditional iris location algorithms often fail to accurately locate the iris. Ensuring the stability and accuracy of iris location has thus become a challenge. In addition, both [4] and [2] utilized the circular template which is not suitable for non-circular boundary. At the same time, the time complexity of these methods is comparatively high with search on a N3parameter space, therefore, the actual application area of these methods is limited.
In seeking to address these challenges, recently,the non-ideal iris images segmentation has gained a tremendous amount of attention, such as[9-15]. In [11],Daugman proposed a non-circular iris boundary localization method which has an extensive applicability.The method uses the active contour line model to locate iris boundary and the Fourier series to smooth it. In[13], Daugman and Tan proposed a PP model for initial location of the pupillary boundary and utilized smoothing spline for precise localization.
3 Matting Based Iris Segmentation
In response to the problems on iris segmentation and inspired by natural image matting algorithm, we propose a novel iris segmentation method. Digital matting technology[16]aims to extract the specified objects of arbitrary shape from a natural image.Therefore, we can apply matting algorithm to divide the pupil, iris and eyelids from original image and locate boundaries with a series of post-processing operations. The flowchart of our method is illustrated in Fig.1.
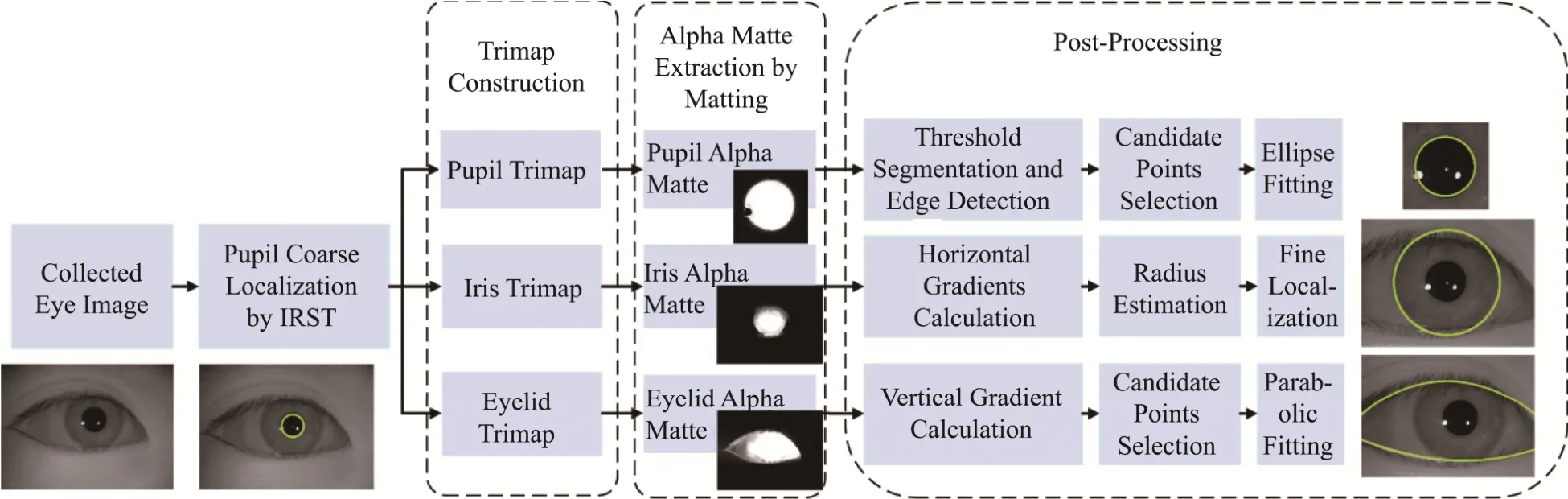
Fig.1 The Flowchart of Proposed Iris Segmentation Method. Five Stages Are Provided, Namely, Pupil Coarse Localization,Trimaps Construction, Objects Extraction Based on Matting, Post-processing
3.1 Matting
How to accurately separating the foreground objects from the image or video is an important problem in the field of computer vision. There are many matting algorithms[17-19] proposed in the field to extract foreground objects from complex sense. Based on in-depth study, matting algorithm is proven more effective in extracting objects.
In [20], the model of matting algorithm was firstly defined mathematically. The problem can be addressed that for an observed image I, it can be seen as a convex combination of foreground image F and background image B as follow:

where α∈[0,1] represents the opacity of the foreground image.
The basic process of matting algorithm is a) determining the objects, b) constructing trimaps, and c)obtaining the alpha matte image. To intuitively demonstrate the equation above, an example is shown in Fig.2 of extracting the iris from a human eye image.For the purpose of precisely locating pupil, iris, and eyelids, the pupil, iris and the region enclosed by upper and down eyelids are determined as the extracted objects. Matting algorithm is used to respectively divide pupil, iris and eyelid from the original image.

Fig.2 An Example of Extracting Iris by Matting. (a)-(f):the Eye Image, the Trimap Image, the Alpha Matte, Foreground Iris and Background Object
3.1.1 Trimap
For a given image I, the foreground image F,background image B, and the alpha matte α of I are all unknown as we can see in Equation 2. Thus, matting algorithm is an under-constrained problem that demands priori information. In general, the priori information is acquired by constructing a trimap. The so-called trimap is to divide the pixels of I into three categories, namely, the set of known foreground pixels labeled as 1 (white region), the set of known background pixels labeled as 0 (black region) and the set of unknown pixels unlabeled. The trimap further indicates that the alpha values of the known foreground pixels and the known background pixels are respectively 1 and 0. Clearly, the trimaps vary in different ways with different extracted objects. What the matting algorithm should do is to estimate the alpha, foreground and background values of the unknown pixels.
According to the practical applications of matting algorithm, trimap construction requires interactive participation on the user’s side. However, in order to apply matting method to iris segmentation, this paper automatically constructs the corresponding trimaps based on the pupil parameters (xpupil,ypupil,rpupil)obtained by RST[21].
3.1.2 Closed Formed Solution Matting Algorithm
According to the matting algorithm in digital image processing, A. Levin, D. lischinski and Y. Weiss put forward a closed form solution matting algorithm in [22]. This algorithm assumes that both F and B are the approximate constants in a local window for a gray image. The iris image meet the assumption as shown in the Fig.3.
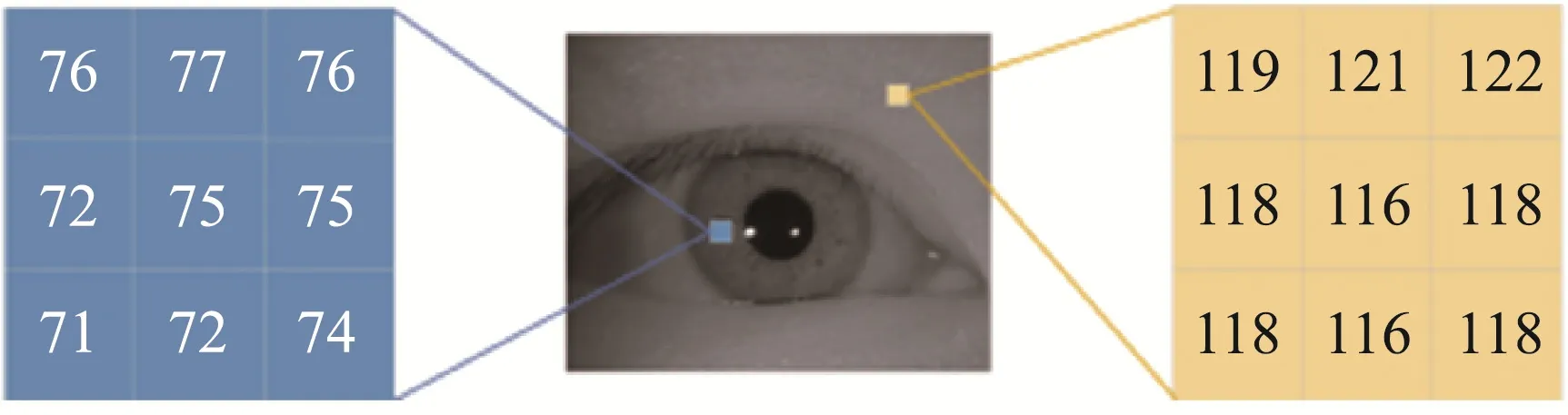
Fig.3 Both Gray Scales of Foreground and Background of Eye Image Are Locally Smooth in 3 × 3 Windows
Therefore, the close form solution matting algorithm is properly applied to divide pupil, iris and eyelids from original image. For a given image I, the Equation 2 can be rewritten in a local window w as follow:


where ωjis a small local window inIand ∊jaj2is a regularization term. The cost function is quadratic in α, a and b, with 3N unknowns for an image with N pixels. It can be proved in [22] that a and b can be eliminated in cost function, therefore, the number of unknowns is reduced, leaving only N alpha values of pixels. After simplification, Equation 4 can be rewritten as follow:

Where L is an N×Nmatrix, called matting Laplace matrix.
According to the prior information provided by the trimap, the alpha values of the known foreground pixels are 1 (α=1) and the alpha values of the known background pixels are 0 (α=0)). For matching these constrains, we solve alpha matte as follow:

Where λ is a large constant in order to make alpha matte is closer to the priori information based on trimap. D is a N×N diagonal matrix whose elements are 1 for constrained pixels and 0 for unknown pixels.αsis a vector containing the specified alpha values for the constrained pixels and zero for all other pixels.
By determining the derivative respect to α on Equation 6 and setting it to zero, we can find the alpha value which makes the equation approach to global minimum. The alpha can be solved as the following sparse linear system:

By solving the equation, the alpha matte is obtained.
3.2 Non-circular Pupil Boundary Localization
In response to the purpose of achieving a more effective iris recognition system and tackling the drawbacks of circle model based pupil localization methods, this paper proposes an effective and robust non-circular pupil boundary localization method based on matting.
3.2.1 Pupil Coarse Localization based on RST
Radial symmetry transformation(RST)[21] is a simple and fast algorithm to detect the interest region with symmetrical property. This algorithm relies on the number combined with gradients of boundary pixels to judge whether there is a circular or circular-like object in image. According to RST method, the initial localization parameters (xpupil,ypupil,rpupil) of pupil boundary are obtained.
3.2.2 Pupil Trimap Construction
Although relatively accurate pupil localization result has been achieved by RST, there is still a general problem for all circle model based pupil localization methods encountering non-circular pupil. In this stage,we construct a pupil trimap Tpupil(x,y) to provide foreground and background priori information for matting algorithm that agree with our perception that pupil should be separated. First, we crop a ROI in-cluding the pupil region based on initial pupil position[xpupil,ypupil,rpupil] provided by RST. Next, with the aim to extract pupil from I(x,y), a circle C1is built with center O(xpupil,ypupil) and radius r1=rpupil−d1.Given the possibility of eyelashes and the upper eyelids obscuring the pupil, only the pixels located in lower semi-circular of C1is considered as foreground priori information labeled as 1. Similarly, to achieve the background priori information, a circle C2is constructed with center O(xpupil,ypupil) and radius r2=rpupil+d2. TThe pixels outside C2are regarded as the known background pixels and labeled as 0. Excluding the known foreground and background pixels,the rest are unknown pixels which are required to be estimated. The generation of Tp(x,y) can be formulated as follow:

Where distirepresents the Euclidean distance between the pixel (xi,yi) and the center O(xpupil,ypupil). I(x,y) is pre-processed by normalized gray-scale. The white and black regions of the pupil trimap are respectively foreground and background priori information, and others are unknown region as shown in Fig.4a.

Fig.4 The Results of Pupil Segmentation in Process.(a)-(e): the Pupil Trimap, the Pupil Alpha Matte Image,Edge Detection, the Pupil Candidate Points and Pupil Localization Result
3.2.3 Pupil Trimap Construction
Observing that the pupil region has smooth gray intensities, with the priori information supplied by pupil trimap, a closed form solution matting algorithm is applied to segment pupil from the original image.Equation 6 is calculated to obtain the alpha matte α as shown in Fig.4b. We can see that the alpha matte has an obvious pupil boundary, therefore functional in locating the pupil boundary.
3.2.4 Pupil Boundary Candidate Points Selection
In this step, threshold segmentation and edge detection are used to acquire the edge points of the pupil alpha matte αpupil(x,y). Firstly, a threshold Tp is given to obtain a binary image Bp(x,y) of αpupil.One characteristic here is that the threshold Tp is unsensitive. The gray values of pupil region and others are obvious different so that the binary threshold Tp can be loose in our method. And then, detecting edge points based on Canny operator obtains the edge points map Ip(x,y) as illustrated in Fig.4c. Aiming at obtaining accuracy pupil points, we develop a noise map based on the initial pupil localization result(xpupil,ypupil,rpupil). Taking the (xpupil,ypupil) and rpupil±5 as the center and radii respectively to structure a ring. The points within the ring are regarded as the reasonable pupil boundary points and the points outside the ring are excluded. In addition, we also exclude the edge points of which the number in a row is more than 5 since that these edge points may belong to the eyelash and light spots. After excluding the noises,the rest points which are taken as the pupil boundary candidate points as shown in Fig.4d.
3.2.5 Ellipse Fitting
Due to the existence of non-circular pupil, ellipse fitting method is a good choice to obtain more accurate pupil position. The representation form of an ellipse is as follow:


To ensure the fitting result is an ellipse, we introduce a constraint b2-4ac<0. In general, we take b2-4ac =-1 as the constraint in order to ensure the existence of the solution. Solve the above constraint problem, we can get the ellipse parameter a→. The results of non-circular pupillary boundary localization are illustrated in Fig.5e.

Fig.5 The Results of Iris Localization in Process. (a)-(d):the Eyelid Trimap Image, the Eyelid Alpha Matte, Absolute Values of Vertical Gradients Image, the Upper Eyelid Candidate Points
3.3 Iris Outer Boundary Localization
In this stage, we propose an effective iris outer boundary localization method based on matting. With our perception to extract the iris, we build a trimap to provide priori information that regards iris region as foreground object. By adopting the closed matting algorithm introduced before, the iris alpha matte is extracted, and subsequently processed by gradients calculation to estimate radius of the iris outer boundary and then fine localization.
3.3.1 Iris Trimap Construction
In this part, we use the similar pupil trimap construction method to generate the iris trimap. For the purpose of extracting iris, the foreground priori information must include iris information. Clearly, the fewer unknown pixels there are, the more accurate the matting algorithm is. Therefore, we generate an ellipse E with center O(xpupil,ypupil), the semi-major axis a in the horizontal direction and the semi-short axis b in the vertical direction. In order to make the foreground priori information encompass part of the iris region,but not beyond its outer boundary, we adopt the adaptive a and b according to rpupil, even if a=rpupil+d3and b=rpupil+d4, 0 3.3.2 Iris Extraction Based on Matting We use a closed-form solution matting approach to extract the iris region which is locally smooth, and thus consistent with the premise of the closed form matting algorithm. By solving the Equation 7 where D and αsare decided by the iris trimap, we can obtain the iris alpha matte αiris(x,y) as shown in Fig.6a. 3.3.3 Finding Maximum Gradient of Multiple Rows We can obverse that the background is darkness while the iris is bright in the iris alpha matte αiris(x,y). Furthermore, the gray value changes noticeably at the boundary of the iris outer circle. In other words, the gray gradient values of the points which are located on the outer circle of the iris are the largest.Based on this observation, we can estimate the radius of the outer circle according to the absolute values of horizontal gradients information of αiris(x,y) as shown in Fig.5b. In general, the centers of the iris inner circle and the outer circle are in a similar position. Therefore, we temporarily assume that the boundaries of iris inner and outer circle are concentric, even ifxc=xpupil,yc=ypupil. The second step is to calculate the horizontal gradient of each row Ri. Based on analysis the alpha matte αiris(x,y), we can see that the pupil boundary also has a clear gradient information. To exclude the interference of the pupil boundary, we set up two effective intervals on rows [1,yc−rpupil−5] and[y,yc+rpupil+5,xSize]. Here xSize represents the transverse dimensions of iris image. And then, we find the maximum horizontal gradient of each row Riwithin the two intervals respectively. Thus 2×(2n+1) iris boundary points of which position coordinates are labeled as (xi,yi) (i=1,2,…,4n+2) are obtained as we can see in Fig 5c. 3.3.4 Radius of Iris Outer Boundary Estimation In order to make the estimation of iris outer radii more accurate, we average the (4n+2) radii, even if Finally, we locate the iris boundary accurately based on the estimated parameter (xc,yc,rc). In order to ensure the positioning results, we further optimization by using Itg-Diff Operator, shown as in Equation 1,which is limited parameters range for fine location of outer circular boundary. The limited parameters range are Δr=3, Δx=2 and Δy=2 which can get a stable position result. The iris segmentation also includes upper and lower eyelids boundaries. It is difficult to correctly determine the eyelid boundaries due to the impact of the eyelash and other variables. This paper propose a method to locate eyelid based on matting. The novelty of our method is that we deal with the alpha image obtained by matting algorithm to locate eyelids. A simplified example would be the upper eyelid localization. The flowchart of upper eyelid localization is shown as Fig.6. Fig.6 The Results of Eyelid Localization in Process. (a)-(d):the Eyelid Trimap, the Eyelid Alpha Image, Absolute Values of Vertical Gradients Image, the Upper Eyelid Candidate Points 3.4.1 Eyelid Trimap Construction In order to locate the eyelid, we regard the region between the upper and lower eyelid as the extracted object. Similarly, we construct an ellipse with center O(xpupil,ypupil) , the semi-major axis a2in the horizontal direction and the semi-short axis b2in the vertical direction. The points located inside the region are considered as foreground priori information. We use two rectangle sections along the image's perimeter as the background priori information since it is requested without the object region. Fig.6a depicts the eyelid trimap description. Here, a2=rpupil−2 since a2must be set up as a small value to avoid wrongly regrading the background region as the foreground priori information when the eyelid interrupts the pupil. With regards to b2, we set it to riris+8 where ririsis the radius of outer iris. 3.4.2 Extracted Eyelid Based on Matting We employ the iris image’s gray scales with the assumption that the foreground and background are both locally smooth. With the original image and the eyelid trimap, the matting algorithm estimate the alpha matte, as illustrated in Fig.6b, in which we can see that the alpha matte image αeyelid(x,y) has an obvious upper and lower eyelid boundary. A series of post-processing on αeyelid(x,y) are introduced in detail as follow. 3.4.3 Vertical Gradients Calculation and Eyelid Candidate Points Selection We calculate vertical gradients of αeyelid(x,y)since that the eyelids are probably close to horizontal and obtain the vertical gradients image Geyelidas shown in Fig.6c. Then, we use a threshold Teyelidto binary the image Geyelid(x,y) and acquire a binary map B(x,y). Two regions of interest are cropped from B(x,y)depending on the iris outer boundary parameter to decrease computational redundancy and improve results accuracy. One ROI marked as Bup(x,y) located above the iris center is used to locate upper eyelid and the other ROI marked as Bdown(x,y) located under the iris center is used to locate the lower eyelid. In order to reduce the number of outliers, we choose only one point in each column. For the upper eyelid localization, we choose the point on the maximum row among the points in the same column of the image Bup(x,y). On the contrary, we particularly choose the point on the minimum row among the points in the same column for lower eyelid localization. In a nutshell, we select the points towards the inside of eye as we can see in Fig.6d. 3.4.4 Parabolic Fitting In this step, we locate the eyelid by parabolic fitting in the original image I since that the shape of eyelid is close to a parabola. The representation form of the parabola is as follow: Here, a, b and c represents the curvature, symmetry axis and intercept of the parabola, respectively.By the experience, we can observe that the curvature of upper eyelid is even smaller, symmetric with respect to the column around iris center. Thus, upper eyelid localization transforms to an optimization problem since we set some reasonable constraints on the parameters a,b, c empirically. In order to verify the efficiency of our method, we carried out a large number of experiments and the iris experimental images mainly comes from the database CASIA-Iris-thousand[23]. This database contains 20000 iris images from 1000 subjects under the less-constrained environment, such as iris with serious noise eyelids, eyelashes, glasses and light spots, etc. It is a challenging task to locate these iris images precisely by traditional methods. The suggested algorithm can achieve accurate and effective results of the iris location in these images. The accuracy of iris segmentation is shown in Table 1 according to statistics. Our experimental results achieve 20.5% and 26.4%, more than the well-known methods integro-differential operator[4]and edge detection combined with Hough transform[2]on iris segmentation rate respectively. It can be seen that our method has a greater performance than the two methods. Table 1 Accuracy Rates Comparison among Our Method, Itg-DIff and Edge-Hough. Fig.7 Examples of Pupil Localization Results. the First Column Is the Pupil Boundary Localization Results of Proposed Method, the Second Column Is the Results of Itg-Diff and Last Column Is the Results of Hough Transform In the stage, we compare the results of the proposed method with Itg-Diff and edge detection with Hough transform methods. The results of our method demonstrates more accuracy than the most well-known two methods as we can see in Fig.8 where the first column is the localization results of proposed method in this paper, the second column is the results of Itg-Diff, and the last column is the results of Hough transform. Fig.8 Examples of Iris Outer Boundary Localization Results. the First Column Is the Iris Outer Boundary Localization Results of Proposed Method, the Second Column Is the Results of Itg-Diff and Last Column Is the Results of Hough Transform Both the Itg-Diff and Edge-Hough approaches employ a circular template to suit the pupil boundary for localization. When the view angle is off-axis,however, there are several non-circular pupil boundaries. Therefore, an ellipse is applied to fit the boundary which is more accurate on dealing with the view axis-off images. In addition, with the existence of round light spots, traditional methods based on gradients are sensitive because the gradients on the light spots boundary are also very large. In the aspect of iris boundary localization,Itg-Diff operate search a circle with the maximum gradient cumulative value in N3which may cause the iris boundary to be incorrectly located on the noises since that the gradient cumulative values of noise is huge, even greater that the iris boundary’s. In addition,if the iris boundary is obscured behind spectacle frame or eyelids, there remains less information regarding the gradients of iris boundary. As a result, Itg-Diff operator requests that the photos be of greater quality. Moreover,the Edge-Hough method first detects the edge points and votes the circle passed by these edge points to identify the iris boundary as the circle with the maximum voting value. The edge points of sounds are also recognized during the edge detection stage. Thus, it is very likely that the Hough transform locate on the noises. Our method not only uses the gradients information, but also integrates the gray information of iris image based on matting algorithm. First, matting algorithm regards image as a combination of foreground and background images with the assumption that the gray of foreground and background images are a constant in the local window. According to the priori information, we extract the pupil, iris and eyelids with clear boundaries. Our method is therefore validated as resistant to noises, showing great robustness and accuract results in contrast to the traditional methods. In general, the iris image acquisition process requires proper illumination. This will consequently result in many problems such as uneven illumination,excessive and insufficient exposure. Using non-ideal images impacted by illumination, a series of complementary experiments is performed to test our method's effectiveness. Fig.9 illustrates the image localization results of our method, Itg-Diff's results, and Edge detection using the Hough transform. Our method has apparently outperformed others on these images. Fig.9 Examples of Complementary Experiment Results. the First Row Is the Localization Results of Our Method, the Second Row Is the Results of Itg-Diff and the Last Column Is the Results of Edge Detection with Hough Transform In this paper, a novel and effective iris localization method is proposed, offering a new research insight -- matting based iris localization on the study of unideal iris image localization problem. The proposed algorithm uses the improved radial symmetry transform algorithm to roughly locate the pupil boundary,followed by the natural image matting algorithm applied to divide the pupil, iris and eyelids from the original image and obtain the corresponding alpha mattes. Subsequently, in order to locate the pupil, the pupil alpha matte is processed by threshold segmentation and edge detection to extract pupil boundary candidate points followed by ellipse fitting. Our task in the stage of iris localization is to calculate the gradients,estimate the radius of the iris outer boundary, and perform fine localization. For the purpose of eyelids localization, we calculate values of vertical gradients in effective region of the eyelid alpha matte image and choose upper and lower eyelids candidate points before fitting two parabolas accordingly. Compared to traditional algorithms, the method has a robustness to non-ideal iris image.

3.4 Eyelid Localization


4 Experimental Result
4.1 Database and Segmentation Accuracy


4.2 Analysis and Discussion
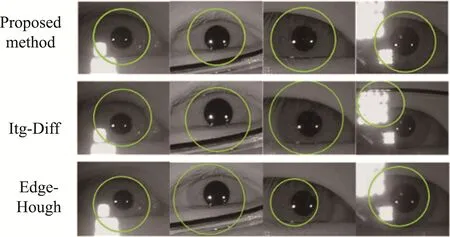
4.3 Complementary Experiment

5 Conclusion
- Instrumentation的其它文章
- Design of a Logistics Automated Guided Vehicle
- Research on Hand-eye Calibration Technology of Visual Service Robot Grasping Based on ROS
- Target Path Tracking Method of Intelligent Vehicle Based on Competitive Cooperative Game
- Research on Surface Defect Detection Technology of Wind Turbine Blade Based on UAV Image
- Time Symmetry Analysis of Nonlinear Parity Based on S-P Compensation Network Structure
- Non-destructive Testing Method for Crack Based on Diamond Nitrogen-vacancy Color Center

