水下狭窄环境中ROV 的自主返回控制

昝英飞，邱天，袁利毫，王会峰，黄福祥，阴炳钢

（1.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001;2.海洋石油工程股份有限公司，天津 300450）

缆控水下机器人是海洋勘探与开发以及协助海洋大型工程等领域不可或缺的重大海洋装备之一[1]。现如今随着海洋事业的高速发展以及考虑潜水员的安全工作深度等，水下机器人需要在更深、更复杂、甚至更狭窄的环境中工作，所需要的工程装备愈发复杂，对其作业精度以及机动性的要求也越来越高，良好的控制系统是达到这些要求的基础[2]。由于自治水下机器人（autonomous underwater vehicle,AUV）对于信号处理的弱势以及需要提前路径规划的原因不适合在复杂、狭窄、未知的环境下工作[3]。因此在这类空间下的工作只有缆控水下机器人（remotely operated vehicle，ROV）才能胜任，为了安全顺利地完成任务，ROV需要具有抗干扰的控制系统以及路径跟踪算法。

ROV 模型具有不确定性与非线性的特点，这需要自适应控制来加强ROV 的鲁棒性，如宋大雷等[4]将无模型自适应控制方法应用于ROV 定深控制当中，仿真结果表明，在定深控制当中，自适应比PID 控制具有更强的抗干扰能力。但无模型仿真仅可验证控制器性能，对实际作业提供的帮助有限。霍星星等[5]针对参数变化、流以及其他未知干扰对深海作业级ROV 位姿控制的影响，设计了基于模糊补偿的ROV 自适应位姿控制器。结果表明该控制器具有良好的跟踪性能、抗干扰能力和鲁棒性。但该论文应用的理想对称数学模型会降低仿真精度。相较于小型观察级ROV，作业级ROV 受到外界的扰动会产生较大的影响，视线导引算法（line of sight,LOS）设计简便，抗干扰能力强，控制效果出色，且在自治水下机器人方面已发展成熟，如郭亦平等[6]采用视线导引法，利用空间几何原理，将空间视线导引法的三维航迹跟踪控制转换为航向角跟踪控制与纵倾角跟踪控制，设计了纵倾模型预测控制算法。陈霄等[7]为提高风浪流等外界环境干扰下，无人水面艇路径跟踪控制的准确性和鲁棒性，提出了两种改进积分视线导引策略，并基于改进导引策略和反馈控制思想实现了无人水面艇水平面的路径跟踪。理论分析和仿真实验证明了算法的有效性和先进性。

本文针对ROV 的非线性以及不确定性，采用反步自适应设计控制器，实现路径跟踪的自主返回，以及动力定位，为ROV 的安全顺利回收提供了方案。本文将反步自适应控制与视线导引法结合，消除位姿、速度、航向的误差，精准跟踪原始路径，达到ROV 的自主返回目的，以及运用ROV的非对称数学模型来提高仿真精度。通过仿真来验证控制器以及路径跟踪算法的可行性。

1 数学模型

1.1 坐标系建立

如图1 所示，为使描述ROV 状态明了与简洁，用两个坐标系对其描述，固定坐标系{n}={N,E,D}，其中N与E构成的平面与地球表面相切。另一个坐标系则为随体坐标系{b}={xb,yb,zb}，也称为动系[8]。

图1 坐标系与ROV 运动参数Fig.1 Coordinate system and ROV motion parameters

1.2 运动学模型

ROV 随体坐标系通过绕坐标轴的3 次旋转可以与固定坐标系重合[9]。因此，ROV 随体坐标系下的速度与ROV 相对于固定坐标系的空间位置之间的转换关系为

式中：V=[vω]T，v为线速度矩阵，ω为角速度矩阵，v=[u v w]T，ω=[p q r]T，Θ=[φ θ ψ]T为姿态 向量，JΘ(η)为转换矩阵，即

1.3 动力学模型

动力学方程可以写为

式中：M=MRB+MA为ROV 的质量矩阵，MRB为ROV 的刚体质量矩阵，MA为附加质量矩阵；C(V)为科里奥利矩阵；D(V) 为阻尼矩阵；MA与D(V)将在1.5 节展开；τ为推进器推力（力矩）；τc为流引起的外部干扰；g(η) 为静力（力矩），其中W、B分别为重力与浮力的数值，xg、yg、zg为ROV 的重心相对于动系的坐标，xb、yb、zb为ROV 的浮心相对于动系的坐标。

1.4 推进器模型

图2、3 为本文引用的ROV 的推进器具体布置。

图2 水平面推进器布置Fig.2 Arrangement of horizontal thrusters

下面引入推进器推力（力矩）公式

式中：T为推进器布置矩阵，K为推力系数矩阵[10]。

u为推进器的输入

将图2、3 中推进器各位置以及角度参数代入推进器布置矩阵T，可在仿真中输出各方向推力（力矩）。

1.5 水动力模型

1.5.1 黏性水动力

考虑到ROV 的一般工作状态（大漂角以及原地回转可以忽略），忽略与角速度有关的二阶项粘性水动力，攻角与漂角的耦合在操作中很少出现，因此也进行忽略，最后通过拘束实验得出阻尼矩阵，即

1.5.2 惯性水动力

若ROV 上下、左右、前后都对称的话，附加质量矩阵除对角线之外所有项均为零。本文引用的ROV 左右对称，前后上下不对称。因此只有附加质量系数λ12、λ14、λ16、λ23、λ25、λ34、λ36、λ45、λ56为零。描述惯性水动力（力矩）时，可用惯性水动力系数来代替附加质量。在水池经过纵荡、垂荡、横荡等实验，得出如下式所示的惯性水动力模型[11]：

本文采用的数学模型水动力参数是基于S.J[12-13]研制的作业级ROV 推导出的。其外形特点为左右对称，前后以及上下均不对称。该ROV 长3.5 m，宽和高均为2 m。由表1 看出，ROV 耦合水动力系数在关于对角线对称的项的大小是不同的，甚至有2 倍的差异。因此对于一般的ROV 建立数学模型时，应用非对称理论是有必要的，不可忽略。

表1 ROV 参数Table 1 ROV parameters

2 控制系统

2.1 控制器设计

针对ROV 模型不确定性和非线性的问题，通过反向递推和反馈线性化，将系统的状态向量转化为误差变量并将其线性化，设计了基于反步法的自适应控制器。通过建立子系统的李雅普诺夫函数递推出整个系统的李雅普诺夫函数，使每个子系统收敛从而保证整个系统的收敛[14]。

控制器的目标是求解出自适应更新率，使位姿误差、速度误差、以及航向误差趋于零，达到路径跟踪以及动力定位的目的。应用全局微分同胚[15]，定义ηp为6×1 向量矩阵，即

式中：ηp为坐标系{b}上的位置和姿态信息，p=[N,E,D]T。对ηp求导再应用和p=Rpp得到

式中：S(ω)为差积算子。位姿误差以及速度误差的表达式为

式中：e1为 位姿误差，e2为速度误差，ηd(t)为期望位置，Vd(t)为期望速度，带有波浪线的参数指的是实际与期望的差值。

2.1.1 位置与姿态的稳定性

2.1.2 速度稳定性

对式（2）提出e2得

式中：Vv为虚拟速度，如果V→Vv，则可满足e2=−K1e1，定义新变量=V−Vv，构造第2 个李雅普诺夫函数：

式中：φ为已知6×11 矩阵；θ为体现了ROV 模型的不确定性，包含未知参数、重力浮力以及流引起的外部干扰的矢量。式（4）简化为

2.1.3 整个系统的李雅普诺夫函数

明确的目标市场。城市节庆活动种类繁多，产品的消费者包括当地居民、旅游者、投资者等不同群体，每种群体的需求和构成各不相同，因此应该在举办活动前就做好充分的调查研究，对消费者进行分类和评价，找出符合营销目标的消费者类型，成功进行产品定位，有利于与消费者之间相互了解和沟通，有针对性地为目标消费群体策划活动内容，从而打造出深受市场欢迎的城市形象。

式中：Γ=ΓT>0，为6×6 正定矩阵。对时间求导得：

设定M、D、g(η)、洋流Vc为常量，即以上参数的导数为零，通过构造自适应更新率

2.2 路径跟踪

2.2.1 视线导引算法

图4 LOS 制导示意图Fig.4 Guidance system of the LOS

要实现路径跟踪的目标为

式中：Δ为超前距离，即e(t)与路径的交点沿着路径向下一个航路点前进的距离。终点为(xlos,ylos)。

当跟踪到最后一个航路点时，ROV 需要缓慢减速直至为零，解决方案如下式

式中：Δs>0 和Δe>0 为速度调优参数。可令ROV在驶向最后一个航路点时速度平滑地下降为零。本文通过手柄操纵ROV 获得轨迹上的航路点，并通过航路点进行路径跟踪实现ROV 的自主返回。

2.2.2 全驱动路径跟踪模式

如图5 所示，在较为狭窄的环境中，全驱动的ROV 相较于欠驱动潜器[19]进行回收作业时，即无法“掉头”的环境中，可以采用“倒车”来解决，且“倒车”对于拥有中继器的ROV 更容易实现回收。

图5 狭窄路径示意图Fig.5 Case of the narrow path

3 仿真模拟

仿真采用“手动操作+路径跟踪倒车返回+动力定位”的形式。依据水下机器人操作安全规范[20]，设定流速为0.5 m/s，与ROV 初始动系纵轴夹角45°。

3.1 仿真结果与分析

本文ROV 的仿真流程为：初始位置设为（0,0,-10），通过手柄操纵ROV，再启动路径跟踪系统使ROV 自动返回，当ROV 返回到原点之后静置一段时间来验证动力定位系统，之后结束仿真。其中，手动操纵、路径跟踪倒车返回以及动力定位的切换时刻分别为：16 s、397 s、1137 s。控制参数、以及路径跟踪相关参数如表2、3 所示。

表2 控制参数Table 2 Control parameters

表3 路径跟踪的各仿真参数Table 3 Simulation parameters for path tracing

图6 示踪图为ROV 通过手柄操纵的操纵路径、路径跟踪的返回路径，以及航路点的集合，流场方向如左下角所示。图7 为示踪图的部分放大，可以清晰地看到操纵路径与返回路径仅有些许误差。

图6 示踪图Fig.6 Tracer figure

图7 示踪图局部放大Fig.7 Local magnification of the tracer figure

图8 为ROV 在仿真过程中的线速度。可以看到ROV 纵向最大操纵速度为1 m/s，之后以0.5 m/s的恒定速度自主返回，在1 102 s 时利用式（7）使ROV 的速度平滑地减小为零。

图8 线速度Fig.8 Linear velocity

图9 展示的是ROV 在仿真过程中的推力。如图9 所示，在仿真过程中根据设计要求，推进器所能提供的最大推力为8 000 N，图9 中的ROV 推力在整个仿真过程中都在最大值以下，因此该推进器满足要求。其中3 处突变是因为手柄操纵、路径跟踪、以及动力定位这3 种模式进行切换造成的。

图9 推进器推力Fig.9 Propeller thrust

图10 为操纵路径与自主返回路径之间的误差，其最大没有超过0.8 m，误差没有达到ROV 宽度的一半，且这与该ROV 的主尺度相比已在合理范围之内，因此该控制器与路径跟踪算法可应用到狭窄环境中，与图11 结合可看出，较大误差出现在斜率较大处，即航向角变化过快处。

图10 偏航距Fig.10 Crosstrack error

动力定位的误差可以从1 137 s 之后看出，误差几乎为零，由图11 的航向角看出，动力定位时航向角也几乎没有误差，说明在有海流的情况下，该控制器抗干扰能力强。

图11 航向角Fig.11 heading angle

选出路径跟踪中的其中一段特征路径与未加自适应的反馈线性化控制器进行推力（力矩）的对比，如图12、13、14 所示，X方向反步自适应推力变化更加平稳，在力与力矩的周期性变化区间上，反步自适应有着更小的超调量。

图12 X 方向推力Fig.12 Thrust in the X direction

图13 Y 方向推力Fig.13 Thrust in the Y direction

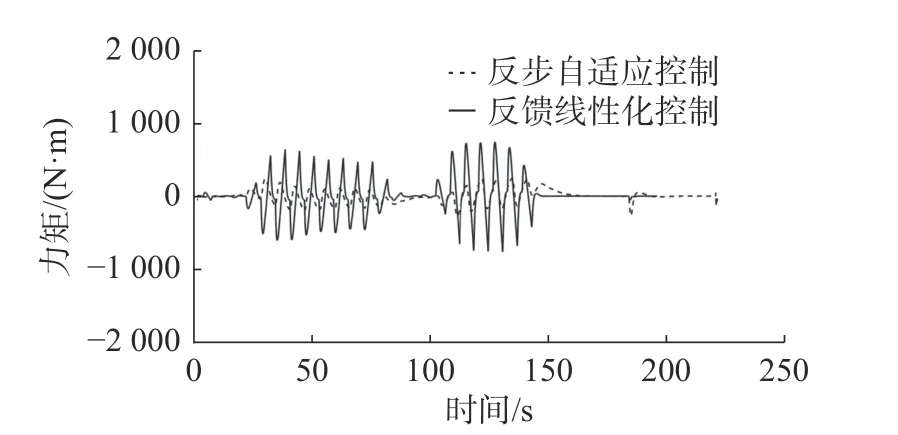
图14 N 方向力矩Fig.14 Torque in the N direction

4 结束语

本文针对ROV 的非线性以及不确定性，将反步自适应控制器与视线导引法结合，消除位姿、速度、航向的误差，精准跟踪原始路径，达到ROV 的自主返回目的。通过分析路径跟踪误差与ROV 本身尺度的关系，得出该控制器可在狭窄环境中完成对大型作业级ROV 的自主返回控制的结论，同时在研究航向角变化中可知，为尽量减小路径跟踪误差，ROV 在实际操作中的航向变化要尽量平缓一些；通过分析动力定位时的位置以及航向误差，得出在有海流的情况下，该控制器具有较强的抗干扰能力；通过推力（力矩）方面的对比得出相较于反馈线性化控制，反步自适应具有更强的稳定性。综上所述，将反步自适应控制器与视线导引法结合，可安全顺利地完成ROV在狭窄环境下的回收作业。