弓长岭露天矿采空区稳定性综合评价

张忠政，王宇驰，宋 贺，李相熙，杨 震

（1.鞍钢集团矿业公司弓长岭有限公司 露采分公司，辽宁 辽阳 111008；2.东北大学 岩石破裂与失稳研究所，辽宁 沈阳 110819）

由于历史原因，弓长岭露天矿台阶下方存在大量采空区。采空区的存在严重降低了露天台阶的承载能力，导致大型机械无法进入采场以开展常规的凿岩爆破作业。这不仅极大地提高了矿石开采难度，而且还降低了开采效率。因此，开展露天矿采空区稳定性的准确评价，能够对弓长岭露天矿的生产设计和规划提供强有力的指导。

针对采空区稳定性的研究，前人开展了大量的工作，并且取得了许多有益的成果。邹友峰等[1]将采空区断裂的顶板岩梁概化为三铰拱式力学结构模型，构建了采空区顶板岩梁失稳的尖点突变模型；黄昌富等[2]分别从结构力学和岩体本构关系2 个角度建立了基于广义H－B 强度准则的矩形采场顶板筒状塌落极限平衡分析模型；周宗红等[3]基于平衡拱理论，对采空区顶板临界冒落面积进行计算分析；赵国彦等[4]采用模糊熵对其进行改进，建立新的采空区稳定性二维评判模型；谢学斌等[5]利用突变理论和流变力学理论对其稳定性及突变倾向性作定量与定性分析。

在对于采空区稳定性的分析中，突变理论[1,2,6]、Mathews 图解法[7-9]和简支梁理论[10-12]等方法被大量应用。也有许多学者为了弥补某一种采空区稳定性评价的缺陷和不足，开始使用多种采空区稳定性评价方法对矿山采空区的稳定性进行多重分析。采用多采空区稳定性评价方法分析得到的采空区稳定性结果可信度和准确程度显著提高。然而，前人采用的多种采空区稳定性分析只是将分析结果简单罗列，缺少对空区稳定性的综合评价。因此，在分别采用Mathews 图解法和简支梁理论分析采空区稳定性的基础上，采用模糊综合评价方法对弓长岭露天矿的采空区稳定性进行综合分析。

1 基于Mathews 图解法的采空区稳定性分析

Mathews 图解法在金属矿地下开采的采场结构设计中被广泛应用。它主要用于计算矿房最大允许跨度。Mathew 图解法[13-15]示意图如图1。Mathews 图解法中的稳定－破坏线、破坏－崩落线将Mathews 稳定图划分为稳定区、过渡区、崩落区3 个区域。

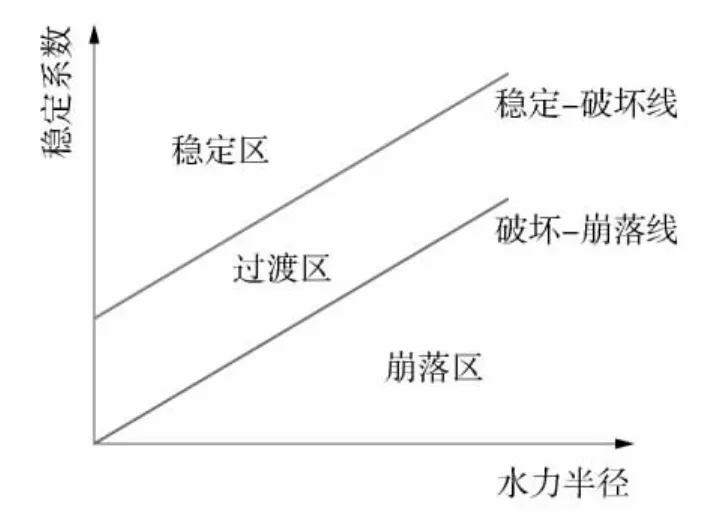
图1 Mathew 图解法示意图

Mathews 图解法综合考虑了岩石质量评价指数RMR、岩石应力系数A、节理产状调整系数B、重力调整系数C 及形状因子S（或水力半径R）等指标，以计算一定应力条件下，和几何条件下矿房能够维持稳定的能力，计算结果直接反映在Mathews 稳定图上的分区中，是一种经验性图解方法。

针对岩石材料的单轴抗拉强度远低于其单轴抗压强度这一特性，Jia 等[16]在现行的Mathews 图解法的基础上，考虑岩体空间多维应力对岩石应力系数A 的影响，基于Hoek－Brown 准则对岩石应力系数A进行修正，并提出岩石应力系数A 的分段计算方法。使用修正的岩石应力系数A 后的Mathews 图解法，对较小尺度采空区的稳定性评价相比于传统的Mathews 图解法，得到的评价结果更符合现场实际状态。

根据弓长岭露天矿采空区的尺寸特征，应用修正的Mathews 图解法评价弓长岭露天矿采空区的稳定性，评价过程如下：

1）确定水力半径R。采空区的水力半径为采空区面积与采空区周长之比，这一参数反映的是采空区的尺寸和形状，其计算公式为：

式中：L 为采空区的等效长度，m；W 为采空区的等效宽度，m。

2）确定稳定数N。稳定数N 的计算公式为：

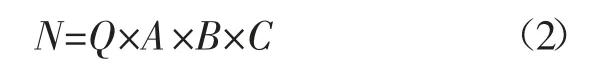
式中：Q 为岩体质量数。

弓长岭露天矿何家采区内某采空区通过以上过程计算得到的采空区稳定数N 和水力半径R，添加到Mathews 稳定图中，根据其在图中的分区位置，得到某采空区的稳定性评价结果是稳定或过渡。

2 基于简支梁理论的采空区稳定性分析

在房屋、桥梁等建筑施工中，梁承载着上部构造的全部质量，主要发生弯曲变形。地下开采形成的采空区，其周围受预留矿柱支撑，顶板承受着上部岩体的质量，受压应力作用后发生沉降，产生轻弯曲变形。因此也可以将采空区顶板简化为两端受支撑的简支梁，可运用简支梁弯曲变形理论来计算、评价采空区顶板的稳定性。

采用简支梁理对采空区顶板稳定性评价：①根据采空区顶板围岩相关岩石力学参数计算出其岩体力学参数；②根据梁弯曲理论计算出几何尺寸已经固定情况下的采空区顶板能够承受的最大拉应力；③比较采空区顶板最大拉应力与顶板抗拉强度的大小，最大拉应力大于顶板抗拉强度则认为采空区不稳定，反之，认为采空区稳定。

根据莫尔－库仑准则计算弓长岭露天矿何家采区某采空区顶板岩体力学参数，得到岩体单轴抗压强度σc和单轴抗拉强度σt与黏聚力c 和内摩擦角φ 的关系为：

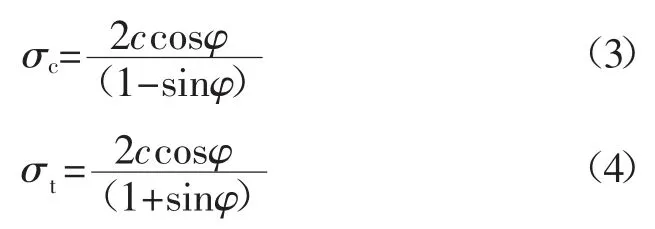
经过对弓长岭露天矿何家采区内岩石的物理力学参数进行测试，得到完整岩石的单轴抗压强度σci＝10 MPa，黏聚力c＝5 MPa，内摩擦角φ＝30°，岩石密度ρ＝3.875 g/cm3，代入计算得弓长岭露天矿何家采区某采空区顶板岩体单轴抗压强度σc＝17.32 MPa，岩体单轴抗拉强度σt＝2.889 MPa。

采空区顶板围岩承受的拉应力为：

式中：σ 为采空区顶板围岩结构中承受的最大拉应力，MPa；L 为采空区顶板跨度，m；h 为采空区高度，m。

采空区顶板跨度L≈117 m，高度h≈20 m，代入式（5）得弓长岭露天矿何家采区某采空区顶板拉应力σ＝0.896 MPa＜σt＝2.899 MPa，因此弓长岭露天矿何家采区某采空区顶板稳定性的评价结果为稳定。

3 模糊综合评价及应用

3.1 模糊综合评价方法

采空区顶板稳定性受到多种因素影响，采用单一的理论、方法很难得到一个较科学、可信度高的评价结果，因此有必要建立一个综合评价模型，对多种稳定性评价手段得到的结果进行综合分析，得到一个能够合理反映采空区稳定性的综合评价结果。

对上述2 种理论分析结果使用模糊综合评价模型，对弓长岭露天矿何家采区某采空区顶板稳定性做出总体评价，并最终给出采空区稳定性预警等级：一级预警、二级预警、三级预警，其中一级预警等级最低，三级预警等级最高。模糊综合评价模型通过有限数量的评价指标（指标1、指标2、…），对采空区稳定性进行评价，它使用层次分析法、隶属度理论等模糊数学相关理论进行多指标综合评价，最终得到一个量化的评价结果（评价集）。模糊综合评价模型可实现定性问题的定量化计算。采空区稳定性综合评价方法流程示意图如图2。

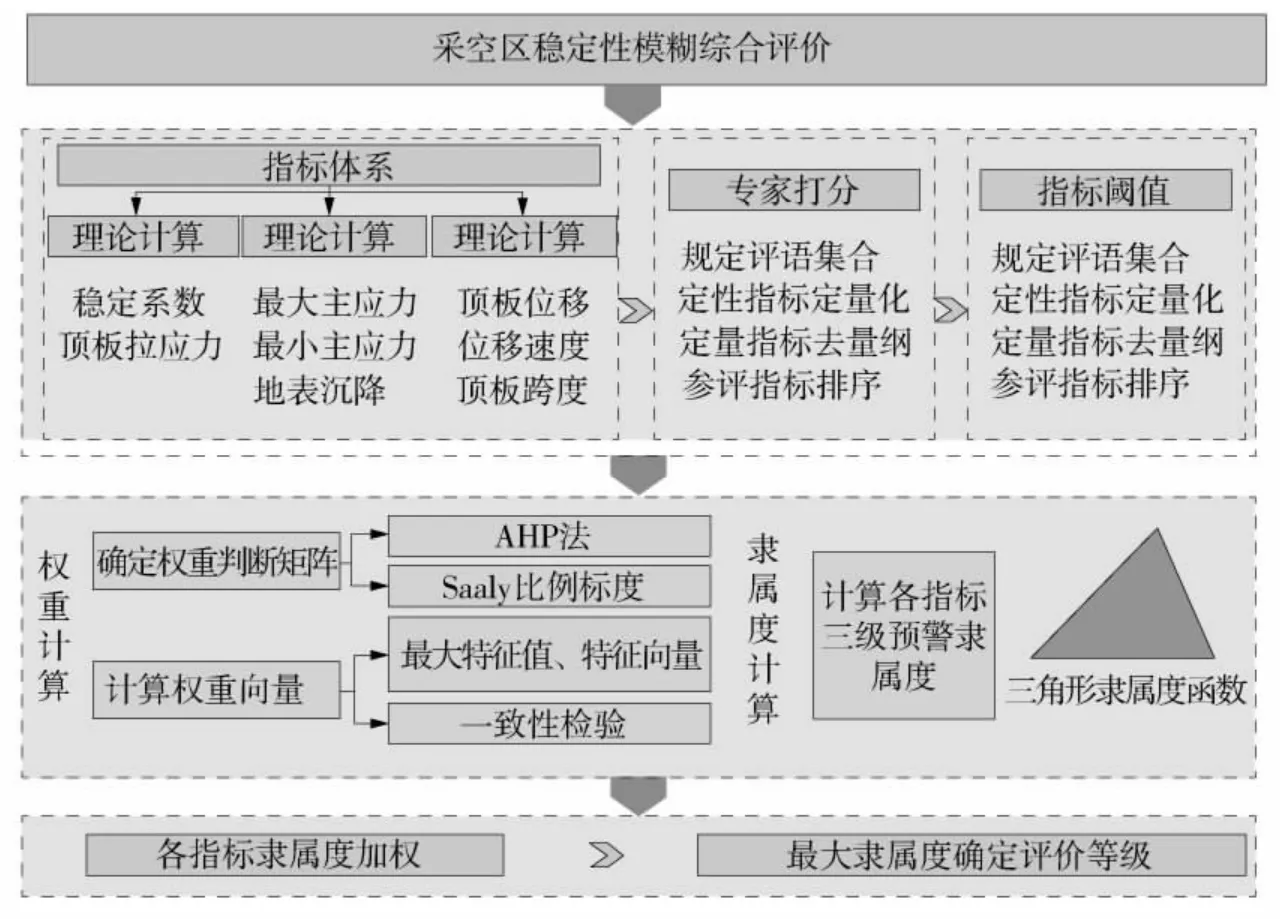
图2 采空区稳定性综合评价方法流程示意图

3.2 模糊综合评价结果

通过上述过程计算得到各参评指标隶属度矩阵和单一评价指标权重，首先将这2 个指标复合得到各分析层隶属度，计算公式为：

式中：b 为1 个分析层的隶属度行向量；r 为对应分析层参评指标权重向量；a 为对应分析层参评指标隶属度。

分析层隶属度矩阵见表1。

表1 分析层隶属度矩阵

运用式（6）进行复合计算得到分析层三级预警隶属度，模糊综合评价结果见表2。

表2 模糊综合评价结果

何家采区某空区稳定性属于“一级预警”状态的隶属度是0.930 9，为3 个等级预警状态中隶属度的最大值，根据最大隶属度原则确定何家采区某采空区处于“一级预警”状态，采空区处于稳定状态，短期内发生失稳的风险较小。

4 结语

为了准确、快速的评价弓长岭露天矿采空区的稳定性，在分别采用Mathews 图解法、简支梁理论分析采空区顶板稳定性的基础上，采用模糊综合评价方法对弓长岭露天矿采空区进行综合判断。以何家采区某采空区评价对象，得到该采空区处于“一级预警”状态，采空区处于稳定状态，短期内发生失稳的风险较小。