风浪震及重力载荷联合作用下大型风力机动力学响应及结构损伤分析

李志昊， 闫阳天， 李 春，2， 岳敏楠， 薛世成

（1.上海理工大学能源与动力工程学院，上海 200093；2.上海市动力工程多相流动与传热重点实验室，上海 200093）

为满足日益增长的电力需求并减少化石能源引起的环境污染问题，可再生能源开发利用逐渐受到各国高度重视。海上风能作为可再生能源中最有潜力的能源之一，近年来发展迅速［1］。据Global Wind Energy Council（GWEC）预测，未来5年内全球海上风电新增装机容量将超过469 GW［2］，未来10年超过40%的新增海上风力机将建于地震频发区［3］，因此地震造成风力机结构破坏的风险不容忽视。单桩式风力机需置于海床内部以保证其稳定性，但我国沿海地区地质条件较为复杂，土-结构耦合效应非线性明显，因而由海底强烈地震引发的海床剧烈震荡更易破坏原有基础的稳定性且易使具有静定结构特性及高柔性的塔架振动加剧，甚至可能引发结构局部失效。因此，保证地震激励下风力机结构安全极为重要。

关于地震载荷对风力机结构安全的影响，诸多学者展开了研究。Kim等［4］基于p-y曲线构建土-结构耦合效应模型并对地震作用下单桩式风力机进行了易损性分析，表明不同土层的地震相位差可能会导致更剧烈的地表运动但风力机动力学响应却更小。Ma等［5］采用响应谱和时程分析法计算了地震作用下风力机动力学响应，表明土-结构耦合效应不可忽略。Yang等［6］以5 MW单桩式风力机模型为研究对象，对比分析了不同土-结构耦合效应模型对地震作用下风力机动力学响应的影响，表明将土-结构耦合效应简化为刚性基础可能会导致风力机动力学响应预估不准确。

此外，海上风力机安装环境复杂，除地震载荷外，还受到湍流风载荷和波浪载荷冲击。Zhao等［7］采用多体动力学方法计算风力机动力学响应，并用风力机轮毂处轴向推力代替气动载荷，发现利用该简化方法计算气动载荷时可大幅提高计算效率，且该简化方法下的动力学响应相差较小。Lesny等［8］基于p-y曲线构建土-结构耦合效应模型，研究了风浪载荷下风力机动力学响应，表明埋土桩基与土反力呈非线性关系。Cao等［9］基于非线性土-结构耦合效应模型对风浪载荷下风力机进行时频分析，表明风浪载荷主要激发风力机一阶模态。Banerjee等［10］采用有限元软件计算了风浪联合作用下5 MW单桩式风力机动力学响应，发现土-结构耦合效应将严重影响风浪载荷下的风力机动力学响应，此外，采用塔顶质量点既可保证一定的计算精度又可大幅节约计算资源。

上述研究仅考虑风浪或地震载荷，而关于风浪震载荷联合作用下风力机动力学响应及稳定性的研究较少。随着海上风力机大型化发展，叶轮及支撑结构直径大幅增加，湍流风和波浪载荷随之增大，加之我国沿海地区地震多发，风浪震载荷联合作用使得风力机塔架动力学响应更为复杂且失稳风险进一步提高，这在评估风力机结构安全时不可忽略［11］。此外，以上研究均采用梁单元进行分析，难以获取局部结构应力应变分布及结构失稳现象，同时在研究结构响应时忽略了重力载荷。目前，为降低度电成本，风力机日趋大型化，重力载荷不断增加，相较5 MW风力机，10 MW风力机叶片、机舱及轮毂等顶部结构和塔架的质量分别增加了326.7 t和852.5 t，塔架高度增加近30 m，柔性大幅增加，导致其更易受风浪震重力载荷而损坏［12］。因此，亟须开展风浪震重力载荷联合作用下10 MW近海风力机动力学响应及稳定性研究。因此，笔者选用丹麦技术大学（Danmarks Tekniske Universitet，DTU）10 MW单桩式风力机为研究对象，采用Kaimal风谱模型建立风场，通过P-M谱模拟波浪，选用实测地震位移数据为地震载荷，对不同环境载荷下风力机进行动力学响应及稳定性研究，为风力机结构安全设计提供参考。

1 研究对象

以DTU 10 MW单桩式风力机为研究对象，模型图及主要参数分别如图1和表1［13］所示，其中X方向为前后向，Y方向为侧向，Z方向为垂向。通过壳单元建立风力机有限元模型，离散模型如图2所示，其中节点数量为1.927 8万，网格数量为1.925万。将叶片、轮毂及机舱等结构视为塔顶偏心质量点，并忽略焊缝、法兰和油漆等因素，为避免风力机质量损失，将模型密度修正为8 500 kg／m3。

图1 DTU 10 MW单桩式风力机示意图Fig.1 Schematic diagram of DTU 10 MW monopile wind turbine

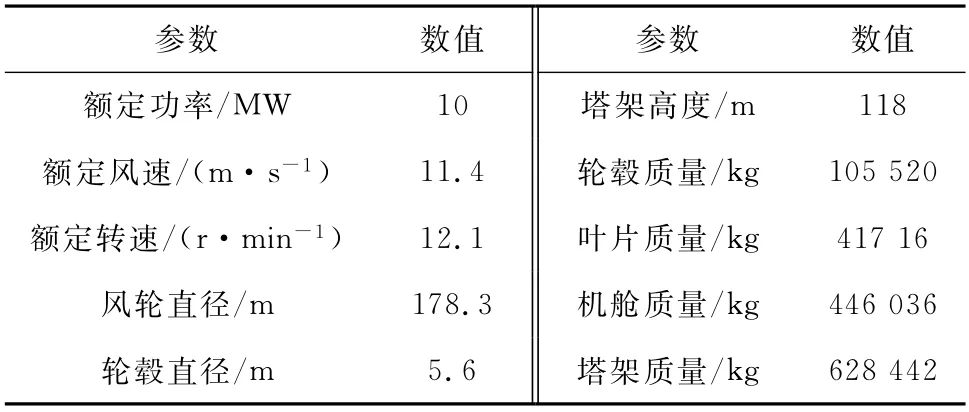
表1 风力机主要参数Tab.1 Main parameters of the wind turbine

图2 风力机有限元离散模型网格Fig.2 Grid of finite element discrete model of the wind turbine

2 环境载荷

2.1 风载荷

通过TurbSim生成风力机轮毂处湍流风场，并假设其3个方向的速度分量相互独立。采用国际电工委员会（IEC）Kaimal风谱模型，其功率谱密度Si（f）为：

式中：f为频率；¯uhub为轮毂处平均风速；M i和σi分别为积分尺度参数和标准差。

基于Kaimal风谱模型生成的湍流风场如图3所示。

图3 额定风速时轮毂处风场Fig.3 Wind field at hub height under rated wind speed

采用叶素动量理论求解风力机气动载荷。将叶片沿展向分解为多段叶素，各叶素间相互独立且互不影响，通过叶素速度三角形计算各叶素上的气动力，并将其沿叶片展向积分，从而求解得到气动载荷。图4为叶素截面示意图。其中，Ω为风轮转速；R为风轮半径；r为叶素展向半径；U∞为来流风速；a和b分别为轴向和切向诱导因子；αi为攻角；βi为翼型扭角；φ为入流角。

图4 第i段叶素截面及速度三角形示意图Fig.4 Schematic diagram of blade element section i and velocity triangle

每个叶素的推力T和扭矩M［14］为：

式中：Cl为升力系数；Cd为阻力系数；ρa为空气密度；c为翼型弦长；W为气流相对速度。

选取风力机运行稳定后100 s的湍流风载荷加载于风力机上，作用位置在风力机塔顶机舱处。

2.2 波浪载荷

波浪载荷可通过莫里森方程和绕射理论来求解。前者适用于计算小尺度结构的波浪载荷，并忽略了结构对入射波的影响，但随着风力机大型化，风力机直径不断增大，其对入射波的影响不可忽略，因此选用绕射理论计算波浪载荷，作用位置在支撑结构处。选取可描述充分发展的波浪的P-M谱描述波浪分布，其功率谱密度［15］为：

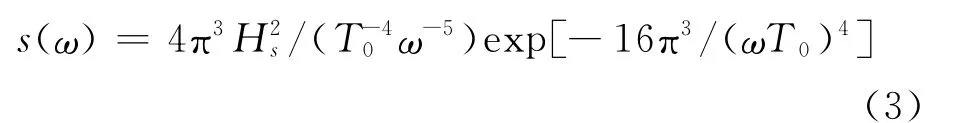
式中：s（ω）为功率谱函数；ω为圆频率；H s为有义波高，取3 m；T0为跨零周期，取6 s。

波浪表面由无限个余弦波叠加而成，其表面运动函数η（t）为：

式中：a k和ωk分别为组成波的振幅和圆频率；εk为0～2π间均匀分布的初相位；k为波数。

基于线性波理论，结构波浪力F1（t）可表示为：

式中：ρw为海水密度；g为重力加速度；D为结构直径；hw为水深；CM为水动力系数；z为笛卡尔坐标系空间坐标。

2.3 地震载荷

为准确描述地震发生时海床运动，从太平洋地震工程研究中心（PEERC）基于全球地震记录建立的PEER NGA数据库中选择真实的地震运动数据。地震发生于Taiwan Chi-chi，震级为里氏7.62级，其地表位移时域曲线如图5所示。

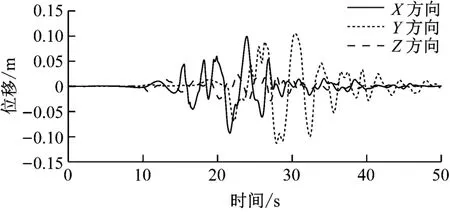
图5 地震位移时域曲线Fig.5 Time-domain curve of seismic displacement

各有限元模型的环境载荷如表2所示。风浪震及重力载荷作用位置如图6所示。

图6 风浪震及重力载荷作用位置示意图Fig.6 Location diagram of wind-wave-earthquake and gravity load

表2 不同环境载荷组合Tab.2 Different combinations of environmental loads

3 土-结构耦合效应

土体响应与结构运动间产生的相互作用称为土-结构耦合效应。海床表面土质偏软，土壤刚度对埋土桩基运动变化较为敏感，导致环境载荷作用下风力机土-结构耦合效应非线性十分明显。为此，选取美国石油协会（API）规范推荐的p-y曲线及非线性弹簧单元建立土-结构耦合效应模型，该模型因应用方法简便及可充分反映土层非线性而广泛应用于近海工程［16］。埋土桩基总长度为30 m，间隔5 m设置垂直于桩基的弹簧以模拟桩周土水平抗力，其示意图如图7所示。

图7 土-结构耦合效应模型Fig.7 Soil-structure coupling effect model

采用API推荐的双曲正切模型计算p-y曲线，计算方法［17］如下：

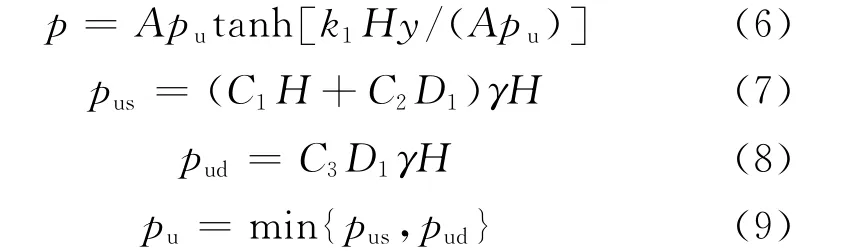
式中：p为桩周土水平抗力；A为修正系数，取0.9；y为桩基水平方向位移（即桩基形变）；k1为地基反力系数；H为距泥面的距离（即土深）；pu为该处土体极限水平抗力；pus为浅层土壤极限土抗力；pud为深层土壤极限土抗力；D1为桩基直径；γ为土体有效重度；C1、C2、C3为与砂砾内摩擦角的相关系数。

土壤参数如表3所示。不同土深处桩周土水平抗力计算结果见图8。

图8 不同土深处桩周土水平抗力Fig.8 Horizontal resistance of soil around piles in different depths

表3 土壤参数Tab.3 Soil parameters

4 有限元方法

4.1 模态分析

模态分析可确定结构的模态参数，即固有频率及模态振型等，为结构振动特性分析提供论据且是瞬态动力学分析的基础［18］。

无阻尼系统中，结构运动方程［19］为：

式中：M为质量矩阵；K为刚度矩阵；u··、u分别为节点加速度和位移向量。

4.2 瞬态动力学分析

瞬态动力学分析可通过求解结构运动方程来计算其在时变载荷下的形变和应力等动力学响应，运动方程［20］为：

式中：C为阻尼矩阵；u·为节点速度向量；F（t）为时变载荷。

4.3 屈曲分析

屈曲为工程设计中结构失效的一种形式，主要表现为当结构承受过大外载荷时，未完全发挥材料强度而失效。通过屈曲分析可获得结构的屈曲模态、振型及临界屈曲载荷。

结构平衡方程［21］为：

式中：Ke和Kg分别为弹性和初应力刚度矩阵；Δu为节点位移增量矢量；pj为结构承受的外载荷。

Kg可由载荷系数λ与单元几何刚度矩阵¯kg乘积求得：

将式（13）代入式（12）可得：

5 网格无关性验证

有限元计算精度随网格尺寸减小而提高，因此需要进行网格无关性验证。根据结构内部最大应变能进行网格无关性验证，不同网格数量对应的最大应变能如图9所示。

图9 不同网格数量对应的最大应变能Fig.9 The maximum strain energy under different grid numbers

由图9可知，当网格数量从6 000增至19 250时，塔架最大应变能逐渐减小最后趋于不变，因此本文中19 250网格数量可保证较高计算精度。

6 结果及分析

6.1 模态

为避免塔架与叶片共振，可通过模态分析获取塔架振动特性，如固有频率及模态振型。通过计算精度高且收敛速度快的Block Lanczos方法提取塔架的前两阶固有频率及模态振型。叶片及轮毂简化前后的固有频率对比如表4所示，模态振型如图10所示。

由表4可知，将轮毂及叶片简化成塔顶质量点对风力机模态特性的影响在允许范围内。由图10可知，塔架一、二阶前后及侧向模态振型分别为前后及侧向弯曲振动，一阶模态振型相对位移峰值位于塔顶，二阶模态振型相对位移峰值位于塔架中部。

图10 风力机前两阶模态振型Fig.10 The first two modes of the wind turbine

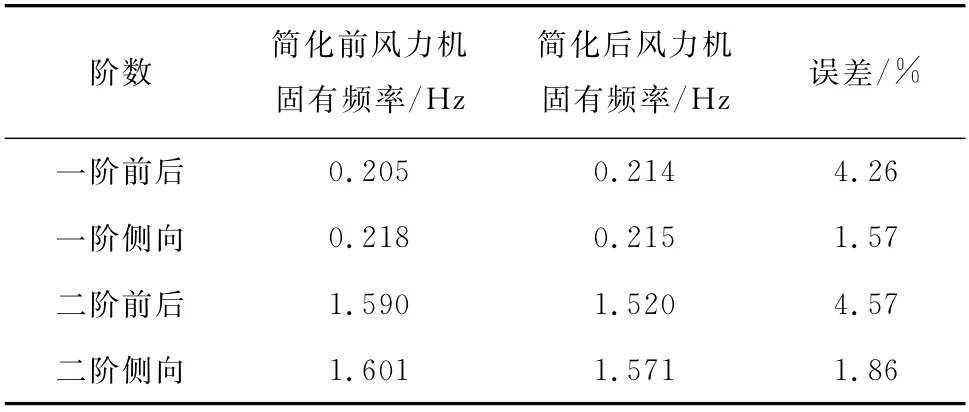
表4 风力机固有频率Tab.4 Natural frequency of the wind turbine

6.2 时域

6.2.1 位移

塔顶位移为反映外载荷下风力机动力学响应的特征响应之一。为观察不同环境载荷下风力机塔架动力学响应差异，输出如图11和图12所示的塔顶前后向及侧向位移时域响应曲线。

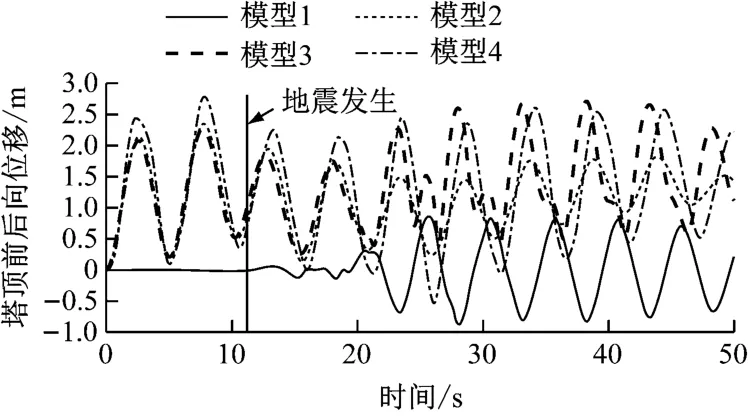
图11 塔顶前后向位移时域曲线Fig.11 Time-domain curve of tower top front and rear displacement

图12 塔顶侧向位移时域曲线Fig.12 Time-domain curve of tower top lateral displacement

由图11和图12可知，不同环境载荷下风力机塔顶前后向及侧向位移时域曲线波动形式有较大不同。图11中，由模型1～模型3对比可知，地震未发生时风浪载荷为引起塔顶前后向位移的主要载荷。地震发生后，海床产生剧烈振动，导致原本仅受风浪载荷作用的风力机塔顶前后向位移急剧增大直至达到峰值且波动形式发生较大改变。模型1～模型3的塔顶前后向位移分别在25.75 s、7.86 s及38.28 s达到峰值，峰值分别为0.862 m、2.35 m及2.71 m，其中模型2的塔顶前后向位移在地震发生前达到峰值。相较于模型1和模型2，模型3塔顶前后向位移峰值增大22.3倍和18.3%。与模型3相比，模型4的塔顶前后向位移在地震发生前达到峰值，且地震发生后，塔顶前后向位移略微减小且其波动周期有明显滞后性。此外，模型1～模型4的塔顶前后向位移标准差分别为0.401 m、0.526 m、0.664 m及0.849 m，相较于模型1和模型2，模型3的塔顶前后向位移标准差分别增大65.6%及26.2%，模型4的塔顶前后向位移标准差较模型3增大27.9%。因此，风浪震载荷共同作用时，地震发生后导致风力机塔顶前后向位移峰值及波动程度相较仅受风浪载荷大幅增大。此外，考虑重力载荷后，塔顶前后向位移波动周期明显推迟且其波动程度进一步加剧。

由图12可知，模型1～模型4的塔顶侧向位移峰值分别为1.42 m、0.018 6 m、1.41 m及1.63 m。相较于模型1和模型2，模型3的塔顶侧向位移峰值分别减小0.71%及增大74.8倍，而相较于模型3，模型4的塔顶侧向位移峰值增大15.6%，模型1～模型4的塔顶侧向位移标准差分别为0.605 m、0.005 99 m、0.603 m及0.704 m，相较于模型1和模型2，模型3的塔顶侧向位移标准差分别减小0.331%及增大99.7倍，模型4的塔顶侧向位移标准差较模型3增大16.7%。因此，塔顶侧向位移主要由地震载荷引起，风浪载荷因其阻尼作用略微抑制塔顶侧向位移峰值及波动程度，而重力载荷则略微增大了塔顶侧向位移峰值及波动程度，且波动周期有明显滞后性。

综上所述，地震发生前，风浪载荷为导致风力机前后向位移主要载荷，地震发生后塔顶前后向和侧向位移峰值及波动幅度均有不同程度增大，其中塔顶侧向位移增幅更大，导致塔顶侧向位移的载荷为地震载荷。此外，风浪载荷显著增大塔顶前后向位移而对塔顶侧向位移有略微抑制作用，重力载荷致使塔顶前后向及侧向位移响应波动更加剧烈，其中塔顶前后向位移波动更剧烈，且使波动周期有一定滞后性。因此，日趋大型化且安装于地震频发区的风力机必须考虑风浪震重力载荷联合作用，否则将导致对塔顶动力学响应预估不足且难以准确预估风力机塔顶位移达到峰值的时间。

6.2.2 等效应力

海上风力机支撑结构设计及建造成本花费巨大，约占总成本50%左右［22］，此外，复杂环境载荷也为支撑结构安全带来巨大挑战，易导致支撑结构等效应力集中，若等效应力过大可能致使支撑结构发生破坏。因此，对风浪震重力载荷联合作用下支撑结构进行等效应力分析十分重要。

图13给出了支撑结构等效应力时域响应曲线。由图13可知，不同环境载荷导致支撑结构等效应力响应峰值及波动产生巨大差异。模型1～模型4支撑结构等效应力分别在26.76 s、7.98 s、38.3 s及23.75 s达到峰值，峰值分别为155.3 MPa、186.5 MPa、224.8 MPa及244.4 MPa，标准差分别为41.1 MPa、42.0 MPa、55.7 MPa及61.8 MPa，相较于模型1和模型2，模型3等效应力峰值分别增大44.8%和20.5%，其标准差增大35.5%和32.6%。相较于模型3，模型4等效应力峰值增大8.72%，其标准差增大11.0%。因此，相较于地震及风浪载荷，风浪震载荷联合作用下风力机塔架等效应力峰值及波动程度都大幅增加，且达到峰值时间也略有延后，此外，考虑重力载荷后，塔架等效应力峰值及波动程度进一步增加。

图13 支撑结构等效应力时域响应曲线Fig.13 Time-domain curve of equivalent stress of the support structure

为进一步观察支撑结构等效应力分布，输出如图14所示的不同环境载荷下支撑结构等效应力达到峰值时的等效应力响应云图。由图14可知，模型1～模型4支撑结构迎风面等效应力峰值均位于支撑结构顶部，而云图中支撑结构中部等效应力灰度值较低，等效应力集聚区域面积相较支撑结构两端明显更小，且云图中相较于背风面，迎风面等效应力灰度值更高，高应力区域面积更大。此外，相较于模型1和模型2，模型3支撑结构处等效应力集聚严重，模型4等效应力集聚更甚。因此，地震载荷将会导致支撑结构等效应力响应更为剧烈，考虑重力载荷后，支撑结构等效应力响应进一步加剧。此外，必须考虑风浪震重力载荷联合作用，否则将对风力机支撑结构等效应力响应预估不准确。

图14 支撑结构等效应力响应云图Fig.14 Cloud image of equivalent stress response of the support structure

6.3 频域

由于塔顶位移时域响应为风载荷、波浪载荷、地震载荷及重力载荷等随机载荷联合作用结果，具有非线性及非平稳特征，需通过频域分析更深入地分析塔架振动特性。通过快速傅里叶变换（FFT）将塔顶位移时域响应转换为频域数据，如图15所示。

由图15可知，模型1～模型4前后及侧向模态的一阶固有频率处均存在明显位移峰值，且相较于模型1和模型2，模型3的位移峰值较大，而模型4的位移峰值最大。但只有模型3一阶前后模态固有频率的二倍频处存在明显位移峰值。因此，地震及风浪载荷仅激发塔架一阶模态，风浪震载荷联合作用下塔架一阶前后模态二倍频处将出现明显位移峰值，而考虑重力载荷后，一阶前后模态二倍频处被抑制。此外，相较地震及风浪载荷，风浪震载荷联合作用下塔架一阶前后及侧向模态处塔顶位移峰值更大，而风浪震重力载荷联合作用下塔顶位移峰值最大。

图15 塔顶位移频域曲线Fig.15 Frequency-domain curve of tower top displacement

6.4 屈曲

随着风力机日趋大型化，塔架柔性逐渐变大，且其结构为偏心受压薄壁结构，这决定了局部屈曲为塔架主要破坏形式之一［23］。因此，对不同环境载荷下塔架进行屈曲分析，表5和图16给出了不同环境载荷下塔架一阶屈曲因子及模态。

表5 不同环境载荷下塔架一阶屈曲因子Tab.5 First-order buckling factor of tower under different environmental loads

图16 不同环境载荷下塔架一阶屈曲模态Fig.16 First-order buckling mode of tower under different environmental loads

由表5可知，相较于模型1和模型2，模型3一阶屈曲因子大幅降低，模型4一阶屈曲因子进一步降低。因此，相较地震及风浪载荷，风浪震载荷联合作用下塔架屈曲风险更大，风浪震重力载荷联合作用下塔架屈曲风险进一步增大，必须考虑风浪震重力载荷联合作用，否则将低估屈曲风险。

由图16可知，仅模型2塔架屈曲区域为塔架底端，而其余模型屈曲区域均位于塔顶，这是由于塔顶壁厚较薄，相较其余地方刚度较小，更易发生屈曲。故工程中需要重点关注塔顶并附加防屈曲装置，以降低风力机在风浪震重力载荷联合作用下产生过大振动而发生屈曲的风险。

7 结 论

（1）风浪载荷为导致风力机发生塔顶前后向位移响应的主要载荷，地震载荷为引起塔顶侧向位移的主要载荷。地震发生后塔顶前后向和侧向位移响应均有所增大，相较于塔顶前后向位移，塔顶侧向位移增幅更大。风浪载荷因其阻尼作用将略微抑制塔顶侧向位移。重力载荷致使塔顶前后向及侧向位移波动更为剧烈，且波动周期有一定滞后性，也改变了塔顶位移达到峰值的时间。

（2）相较于地震及风浪载荷，风浪震载荷联合作用下支撑结构等效应力响应更大且波动更为剧烈，考虑重力载荷后等效应力响应进一步增大。不同环境载荷下塔架等效应力均集中于支撑结构上部。相较背风面，支撑结构迎风面等效应力集聚更严重。

（3）风力机结构设计时必须考虑风浪震重力载荷联合作用，否则将导致风力机动力学响应预估不准确。

（4）不同环境载荷下塔架前后及侧向一阶固有频率处均存在明显位移峰值，即一阶模态被环境载荷诱发。此外，风浪震载荷联合作用下塔架一阶前后模态频率在二倍频处出现明显峰值。考虑重力载荷后，一阶前后模态二倍频处被抑制。

（5）不同环境载荷下，塔架屈曲因子略微不同。相较于地震及风浪载荷，风浪震载荷联合作用下一阶屈曲因子大幅降低，更易发生局部屈曲，考虑重力载荷后，一阶屈曲因子进一步降低。此外，塔顶为易发生屈曲区域，在工程设计时应重点关注此处，可通过附加防屈曲结构等方式增大塔顶刚度。