基于遗传LM算法的电力物资自动化统计方法
吴凤梅,李禹梁,王 涵
(江苏电力信息技术有限公司,江苏 南京 210009)
近几年,随着用电需求的不断扩大,电力企业开始大力发展农村电网和城市电网的建设改造。但在电网的建设改造过程中,存在庞大的工程量,且涉及的电力物资也是数量巨大且繁杂的。就城市电网改造而言,一个城市涉及到的电网建设工程有成百上千个,涉及的电力物资多达上千种。而在实际的工程施工中,常常出现材料采购库存与实际用量不符,数量过多或者数量不足均会影响工程的施工进度。要求电力企业对电力物资的库存量、需求量以及成本进行多方面考量,在满足施工进度的同时减少电力企业资金压力。如何对电力物资的库存进行高效率统计成为当前研究的热门话题。
文献[1]依托“储检一体化”物资抽检模式,通过对自动化抽检方法的研究和自动化检测设备,自动化制样设备,信息化管理系统的应用双管齐下,保证物资检测完成率100%。文献[2]提出一种改进GM(1,1)动态预测模型,结合库存管理方法,构建应急物资动态需求模型,该改进GM(1,1)模型具有可行性与实用性,比传统GM(1,1)模型具有更高的预测精度。但上述方法统计结果精度较低。
本文在遗传LM算法的基础上,提出一种电力物资自动化统计方法。将电力物资分为基建物资和常设物资两种,分别对其采取不同的统计方法。常设物资又分为常用物资和应急物资,本文选择的概率累积法,应急物资则选择的是计算最小期望值的方法。仿真实验也验证了本文方法在统计电力物资方面的有效性。
1 遗传LM算法实现过程
1.1 遗传算法下收敛性控制
遗传算法常常与神经网络一起出现在算法中,将神经网络输出的能量函数E,代入到遗传算法中,作为适应度函数F的基础,使F=C/E,其中,C为一个常数项。将得到的新个体与其他个体进行比较,在最相似准则的基础上选取与新个体最相似的个体,并将新个体替换掉。通过欧式距离对相似性计算结果进行定义,如式(1)所示:
dist(Indi;Indj)=wx(ED(xi;xj))+wF(ED(fi;fj))
(1)
式中:
(2)
式(2)表示个体xi与个体xj之间的欧式距离。wx、wF分别为ED(xi;xj)、ED(fi;fj)权值大小;k为迭代次数。
在遗传算法中,通常有两种情况可以对子代和父代进行个体转换:
(1)将所有新产生的个体均看作为子代,整体对父代个体进行替换;
(2)通过对新产生的个体与原始个体进行比较,保留较优的个体进行下一代的迭代。
在这两种情况中,第一种对于全局寻优有非常明显的优势,但是收敛效率不理想;第二种情况的收敛速度显然高于第一种,但是极易陷入局部寻优。为平衡这两种情况,本文通过对新产生个体的周期性进行观察,每隔L代用新产生的个体替换旧的个体,而不是利用最相似准则。
1.2 基于LM算法的统计精度控制
LM算法是将梯度下降法与高斯-牛顿法的优点集为一体,通过标准的数值优化技术实现快速运算。
将x(k)定义为第k次迭代计算时权值和阈值构成的向量,新得到的权值和阈值构成的向量x(k+1)可通过式(3)计算得到:
x(k+1)=x(k)+Δx
(3)
高斯-牛顿法则是通过以下形式实现[3]的:
Δx=-[∇2E(x)]-1∇E(x)
(4)
式中:∇2E(x)为误差指标函数E(x)的Hessian矩阵;∇E(x)为牛顿法的梯度信息[4]。
将E(x)定义为式(5)的形式:
(5)
式中:e(x)为误差函数,L为遗传算法层次。则可以推理得到:
(6)

(7)
高斯-牛顿法的计算法则规定:
Δx=-[JT(x)J(x)]-1J(x)e(x)
(8)
LM算法在高斯-牛顿法的基础上做了部分改进[5],如式(9)所示:
Δx=-[JT(x)J(x)+μI]-1J(x)e(x)
(9)
式中:μ>0为常数,I为单位矩阵。
通过式(9)的计算可以看出,当μ=0时,还是高斯-牛顿法;当μ的取值越来越大时,趋向于梯度下降法这样一来。高斯-牛顿法在控制误差[6]方面,计算的速度越快,误差精度控制得也就越高。由于LM算法中引入了近似的二阶导数信息,在计算过程中,大大提高了计算效率。不仅如此,由于JT(x)J(x)+μI是正定的,所以式(9)是可以随时求解的。通过式(9)来修改一次权值和阈值时,需要求解n阶的代数方程。LM算法的计算复杂度为O(n3/6),当n的值较大时,计算量和复杂程度普遍[7]偏大。但是,还是可以很明显地看出,迭代计算的效率在不断提高,对于算法的整体性能都有所改善,尤其是在误差控制方面,具有极高的精度。
1.3 遗传LM算法流程
本文在遗传LM算法的基础上,针对电力企业提出了一种新的算法-GALM算法。首先,通过遗传算法改善电力物资数据的整体质量,结合LM算法进行训练。GALM算法的计算模型如图1所示。

图1 GALM算法计算模型
从图1GALM算法的整个计算过程中可以看出,每一种算法都被限制在其特定的范围内。一方面,由遗传算法来确保整个计算过程的全局收敛性[8],避免高斯-牛顿法陷入局部寻优状态;另一方面,遗传算法与LM算法的结合,对于提高搜索效率非常有效。由此可以得出,GALM算法具有较优的收敛性,不仅如此,在降低算法依赖性的同时还确保了算法的收敛方向,即使在对问题内在联系较少的情况,依然可以得到对电力物资数据很好的训练结果。
2 电力物资统计方法实现
在电力企业工程改造项目中,通常根据电力物资的使用情况将其大致分为两类:一类是根据改造项目所需材料建立的物资供应;另一类是用于日常维护所需要的物资,这类物资的特点是数量少、种类杂。根据电力物资的特点以及对电网改造工程的重要程度[9],将其分为A、B、C三类,并且分别采取不同的管理方式,具体如表1和图2所示。

表1 电力物资的ABC分类
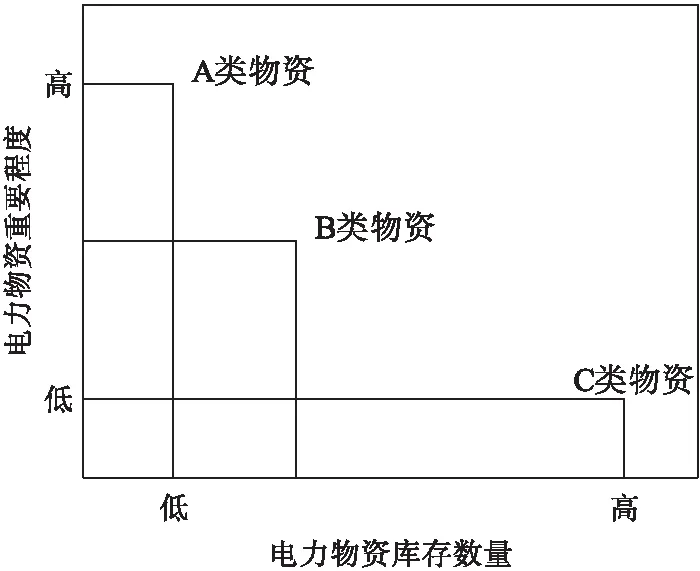
图2 电力物资的ABC分类
2.1 基建物资库存统计方法
在电网改造项目中,基建类物资种类较少,但是数据却很多,通常具有较高的经济价值。对于此类物资的库存管理方法,采用的是零库存,有需要直接由工厂运输到施工现场,减少二次搬运所花费的时间和成本费用。对于没有预料到的情况,可暂时积压在仓库。对于此类物资的统计方式就是定期盘点,提高库存周转效率。
2.1.1 定期统计库存
经调查走访发现,在部分电力物资仓库内存有一定量的废旧物资,这些废旧物资中可以回收再利用的非常有限,大多属于报废物资或者等待报废。这样一来,这些废旧物资不仅占用了相当一部分的仓库空间,而且也增加了仓库维护费用。因此,定期对库存进行统计,不仅可以使电力物资保持在一个正常的运转周期内,而且可以制定详细的采购清单,同时也能提高仓库的存储效率。
基建类物资库存统计方式主要有以下三种:永续统计[10]、巡回统计和全面统计。
永续统计就是每次在物资出库/入库时就做好物资数量的记录,并且随时核对数目;巡回统计就是针对出库/入库较为频繁的物资进行重点跟踪,使其库存数量始终保持在一个稳定的状态下;全面统计就是每年的6月份、12月份,集中对仓库内物资进行全面清点,并做好相应的记录。
为了降低统计过程中物资数量与实际数量之间的误差,本文利用ABC概念图对统计过程进行指导,并对库存细项进行具体的计算。
2.1.2 提高电力物资周转效率
电力物资周转效率指的是在一段时间内,某项物资库存周转的速度,可通过式(10)计算得到:

(10)
通过对电力物资的合理管理以及库存统计,及时了解各类物资库存信息,避免因库存过多导致物资积压,出现报废的情况。
2.2 常设库存统计方法
在常设库存中,将电力物资分为常用物资和应急物资两类。常用物资就是施工中常用到的材料,出入库较为频繁,对于此类物资应随时记录库存量,并且做好相应的周转工作,提高库存周转率。应在出入库时记录清楚数量以及库存数量并定期进行核对,按照施工需求及时调整库存;应急物资也就是抢修、抢险类物资,这类物资的需求情况前期很难预测到,考虑到仓库的维护成本,通常不会有大量库存。所以在对其进行库存统计和管理时,应考虑到缺货损失与库存成本之间的关系,在确保施工抢险工作正常进行的前提下,做好库存数量的安排,合理、有计划地进行采购。
2.2.1 常用物资库存数量确定方法
常用物资在电网建设中定期或不定期都会进行更换,使用需求很难掌握,为了使电力工程有序进行,确保各类物资供应到位,本文采用了概率累计法来确定常用物资的库存数量,设置一个最低需求量,以维持电网工程的正常运行。
2.2.2 应急物资库存确定方法
电力工程施工环境复杂且不确定,对于物资的损耗也较大。一旦出现紧急情况,必须及时采取措施将损失降到最低。但是,紧急情况的出现也具有很大的随机性,再加上应急物资的制备时间较长、成本较高,一定周期内只能订货一次,如果没有到期物资已经用完不能补充订货;如果没有出现紧急情况,物资没有用掉,这个周期内也不能再订货。所以,对于应急物资的库存数量确定有一定难度。
本文对损失期望值最小的库存备件数量Q进行计算,如式(11)所示:
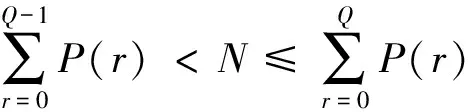
(11)
式中:P(r)为某个设备损坏需要r个库存备件的概率值;N为损益转折概率值。
(12)
式中:l为边际收益;h为边际损失。
假设某个电力物资仓库因某个设备的损坏导致20处电网施工项目被迫停止,该设备的价格为500元,停工损失为10 000元。通过统计资料计算,20处电网项目需要更换r个库存备件的概率如表3所示。

表3 更换r个库存备件的概率P(r)
在保证损失期望值最小的前提下,确定该设备备件库存数量的方法如下:
(1)当电网出现紧急情况时,可通过更换设备备件避免损失10 000元,所以可得到边际收益为l=10 000-500=9 500元。
当设备备件库存数量过多时,多采购一个备件就损失500元,所以可得到边际损失h=500元。损益转折概率值可通过计算得到,为0.95。
(2)根据表3计算得到设备备件的累计需求概率值为
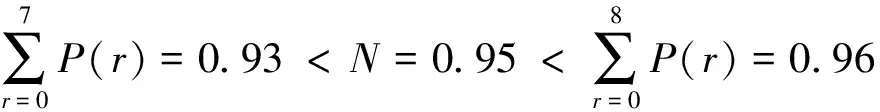
(13)
因此可得Q=8,即当备件数量为8时,可将损失期望值降到最低。
3 仿真实验
为验证本文方法在统计电力物资库存时是否合理有效,对其进行残差检验。实验在Windows2010系统上实现,以Microsoft Visual sTUDIO2008作为开发平台。实验数据来自某电网改造工程配套的电力物资存储仓库。实验过程如下所示:
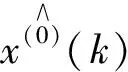
残差:
(14)
相对残差:
(15)
(2)分别进行验差检验。
x(0)的均值:
(16)
x(0)的方差:
(17)
残差的均值:
(18)
残差的方差:
(19)
(3)计算后验差比值和小误差概率值。
后验差比值:
(20)
小误差概率值为
(21)
(4)统计结果精度等级评价标准如表4所示。

表4 统计结果精度等级划分
根据上述残差检验方法,对本文方法统计的电力物资数量进行检验,所得结果如表5所示。

表5 本文方法残差检验结果

4 结 论
针对传统方法在统计电力物资库存时,常常与实际库存数量相差较大,为此,本文在遗传LM算法的基础上,提出一种电力物资自动化统计方法。根据电力物资的出入库频率和重要程度,将其分为基建物资和常设物资两种,常设物资又包括常用物资和应急物资,分别对其采取不同方式的统计方法。仿真实验中,对所提方法进行残差验证,结果表明,所提方法具有较高的统计精度。

