管壳式相变双层换热管设计与数值分析
李昌亭,白 帆,林春城
(陆军装甲兵学院士官学校 车辆运用系,吉林 长春 130117)
随着社会经济的快速发展,能源短缺问题已日益突出,世界各国研究学者正在努力寻找可替代能源,以解决当今世界面临的严峻挑战。当前,所有目光都集中在了新能源方向,比如风能、水能、太阳能等,这些自然界中存在的能源,是取之不尽用之不竭的,所以新能源的崛起势必将会对社会科技的发展带来革命性的突破。但是,随着新能源的迅速发展,新能源的缺点也日益显现,比如新能源消纳能力不足、弃光弃风形势严峻、环境问题逐渐凸显等。为了解决这些问题,科研人员加大了对储热技术的研究,因为储热技术是提高能源利用率和保护环境的重要手段之一[1-2]。
相变储热技术因单位体积储热量大,储热和放热过程温度基本恒定等优点而成为目前研究储热技术的重点,而其中管壳式相变储热装置由于其结构简单、安装方便、成本低廉等优点,成为相变储热技术研究的热点之一。胡延铎[3]等对管壳式与圆柱式梯级相变蓄热装置进行了数值模拟与比较分析,最后得出管壳式装置更利于传热,传热性能更佳。王美俊[4]等采用数值模拟的方法,对管壳式换热器蓄热单元进行了数值模拟与优化,对光管结构和翅片换热管的计算仿真结果进行了对比分析。范宗良[5]等应用Fluent流体仿真软件,对一种新型的Y型纵翅片管式相变蓄热器进行了仿真研究,结果表明,相变材料熔化时间缩短,效果显著。Lacroix[6]采用仿真计算与试验的方法,对双层换热管进行了分析研究,其中心管通过换热流体,外壳侧填充PCM,并针对不同管径、流体速度和进口温度条件下的工况进行计算和试验。Khan[7]等利用二维有限元分析软件,建立了一种新型结构的管壳式相变蓄热器,并对其进行了仿真计算。王乐李[8]等采用数值方法分析管壳束相变蓄热器的蓄热性能,通过建立数学模型、网格划分和耦合计算等过程,分析了入口速度、入口温度及相变材料体积对蓄热器蓄热性能的影响。
从已有的相关文献和科研成果中,可以发现很多的科研人员都把目光集中在同一种结构的同心换热管中,只对一种结构的同心换热管展开相关研究,缺乏了不同结构同心换热管对研究结论的影响分析。针对此种不足,本文拟对不同结构的双层同心换热管放热性能展开研究,其换热材料选用相变蓄热材料。
1 建立双层换热管计算模型
本文应用Ansys Workbench中的Ansys Design Modeler(简称DM)三维建模软件[9-10],对双层同心换热管进行结构设计,在本文中主要研究双层同心换热管中的中心换热管直径对其换热性能的影响,需保证外层换热管与中心换热管体积之差不变,即相变材料体积始终不变。
为了节约计算机计算空间,减少计算时间,对双层同心换热管进行简化处理,其计算模型如图1所示,根据此计算模型共设计了8种不同结构的双层同心换热管,其几何参数如表1所示。在换热管模型中,只要保证面积S不变,就可以保证外层换热管与中心换热管体积之差不变,即相变材料填充的体积不变。

图1 双层同心套管简化计算模型
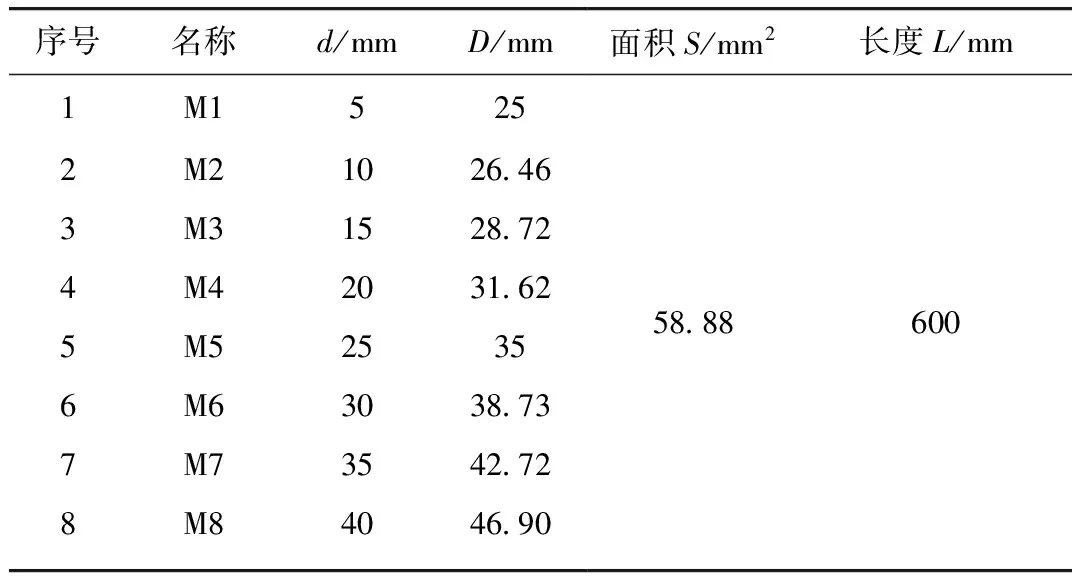
表1 计算模型几何参数
2 网格划分
本文利用Mesh前处理软件对模型进行网格划分,考虑到三维套管是轴对称的,在网格划分和仿真计算过程中,可将套管模型简化为二维计算模型,如图2所示。根据二维计算模型设定计算域,中间流道设置为流体通道,两端分别为进口和出口;在流道两侧为储存相变材料空间,即套管外管空间。
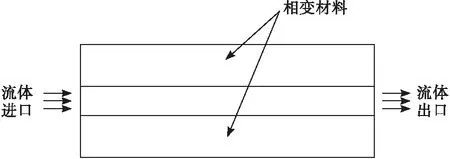
图2 二维计算模型
在处理网格时,采用均匀分布的四边形网格,根据表1中的模型数据,生成的网格数量如表2所示。

表2 各模型网格数量
3 相变传热数值求解方法
本文采用Fluent流体仿真软件对上述换热管模型进行计算,由于换热管外壳中填充的材料为相变蓄热材料,因此Fluent在计算其凝固/熔化时,通常采用连续性方程、能量守恒方程和动量守恒方程进行求解。在Fluent软件中,引入液体组分(Liquid Fraction)来表示液相比例,并采用焓-孔隙率的方法处理凝固/熔化过程。
为了方便计算和仿真,提出以下几点假设条件:①PCM各向同性;②换热管热阻忽略不计;③PCM固液两项的物性参数不随温度变化而改变;④PCM计算过程中不存在过冷或过热问题,只在给定温度范围内发生固液相变;⑤相变过程发生在一个温度区间,焓与温度关系认定为线性的[11]。
基于以上假设及材料热力学相关理论[12],可得到其控制方程,其中式(1)为连续性方程、式(2)为能量方程、式(3)为动量方程:

(1)
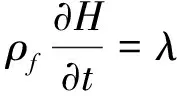
(2)
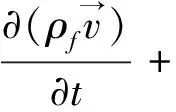
(3)
其中:
(4)
式中:ρf为HTF的密度, kg/m3;t为凝固时间,s;λ为导热系数,W/(m·K);μ为动力黏度,kg·s/m2;cp为定压比热容,kJ/(kg·K);H为任意时刻的焓值,kJ/kg;href为初始焓值,kJ/kg;L为相变潜热,kJ/kg;β为液相体积分数。
液相体积分数β可用式(5)进行表示:
(5)
式中:T为HTF温度,K;Ts为相变材料凝固温度,K;Tl为相变材料融化温度,K。
液相体积分数β的含义是当相变材料完全为液体时其默认值为1,相变材料完全为固体时为0,而两相混合状态时处于0~1。
4 仿真计算
4.1 计算条件设定
将8个换热管模型网格分别导入Fluent中进行计算,其中求解类型设定为基于压力、绝对速度、二维、瞬态模式,同时激活Energy方程和Solidification&Melting方程[13-14]。材料设定时,换热管材质设定为不锈钢“Steel”,而相变蓄热材料采用的是64号石蜡,通过Fluent中的User-defined database进行设置,换热流体为空气,其物性参数如表3所示[15]。

表3 64号石蜡物性参数
在进行边界条件设置时,换热流体的入口温度为298.15 K,入口速度为3 m/s,相变蓄热材料的初始温度为338 K,换热管模型外壁面设置为绝热,内壁面耦合,计算时忽略换热管壁面厚度,出口边界条件设定为outflow;在进行求解时,采用速度耦合的方式,选用SIMPLE算法,运用二阶迎风差分格式,其他设置为默认值;迭代求解时,步长设置为1 s,对于放热凝固过程,迭代计算到相变材料完全凝固为止,计算结束。
4.2 仿真计算
通过Fluent软件对上述8种换热管模型进行仿真计算,其中M1模型计算过程中液相组分比例云图如图3所示。

图3 M1热管模型仿真计算液相组分比例
其他7种换热管模型的参数设定和计算过程与M1完全相同,通过计算可发现,不同换热管模型中相变蓄热材料完全凝固的时间不同,如表4所示;当相变材料完全凝固时,换热管出口温度也不相同,如表5所示。

表4 相变材料完全凝固时间 s
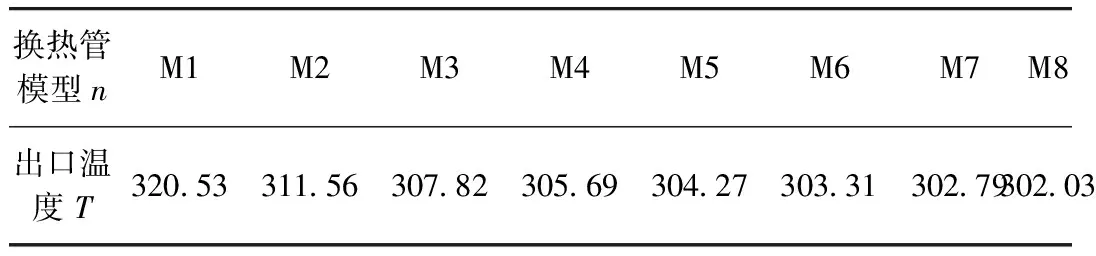
表5 相变材料完全凝固时换热管出口温度 K
4.3 计算结果分析
根据表4中的计算结果,可以得到n与t的关系曲线,如图4所示;根据表5中的计算结果,可以得到n与T的关系曲线,如图5所示。
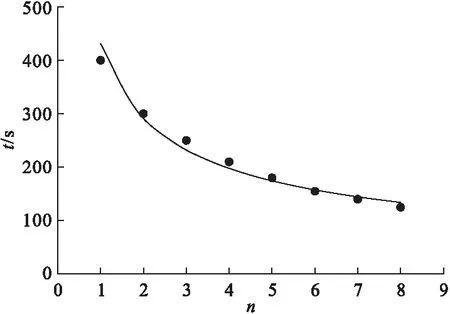
图4 n与t的关系曲线
由图4可知,随着双层换热管中心管直径d的增大,并在相变材料体积不变的情况下,相变材料完全凝固放热时间t随之减少。出现这种现象是由于中心管直径d增大,会使相变材料与换热流体的间接接触面积增大,换热时间随之减少,因此相变材料的完全凝固放热时间t减少。但是通过图4还可以发现,相变材料完全凝固放热时间t一开始下降的速度比较快,随着中心管直径d的继续增大,虽然相变材料完全凝固时间t继续减少,但是其下降的速度趋于平缓,即下降速率减小。
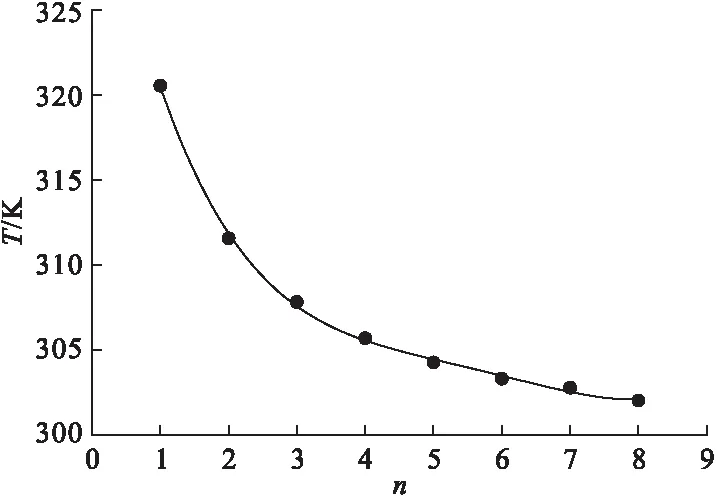
图5 n与T的关系曲线
本文涉及了相变材料的凝固放热计算,相变材料凝固时会向外放热,换热流体将相变材料放出的热量吸收,使换热流体的温度升高,即每个换热中心管的出口温度T都会升高。由图5可知,在相变材料体积不变的情况下,换热流体的出口温度T随换热中心管直径d的增大而减小,这是由于相变材料体积不变即放出的总热量不变,因此换热流体的出口温度T随换热流体体积增大而减小。通过图5还可以发现,不同换热管模型的出口温度T随换热中心管直径d增大而减小幅度变小,即n与T的关系曲线越来越平缓。
5 结 论
(1)在所设定模型参数下,换热管中心管直径d的变化会使相变材料完全凝固放热时间t和换热流体出口温度T同时发生变化,其变化趋势的特点基本相同,随着d的增大,t和T都随之减小,曲线比较平滑,但曲线并不是线性的;t和T随着d的增大不断减小,曲线一开始比较陡即下降速度比较快,但随着d继续增大,曲线开始趋于平缓,下降速度明显减小。
(2)通过本文研究,在研制双层换热管时,应该对不同模型参数进行计算,根据实际应用环境和要求选定合适的换热管参数,并不是d越大越好,相反也不是d越小越好,应该综合考量和设计。在本文计算结果中,根据所设定模型参数,建议选用M4即中心管直径d为20 mm的换热管,与M1相比相变材料完全凝固放热时间缩短47.5%,换热流体出口温度也相对较合适。

