自动化设备外表面腐蚀区域激光清洗技术研究
李萌锋,黄少敏,林燕强
(国网泉州供电公司,福建 泉州 362000)
现阶段,随着各类重工业技术类产业链的不断发展和扩张,带动了各类自动化技术的应用,而自动化设备作为各工业重点的机械设备之一,在生活及生产等各个领域都发挥着重要作用。然而,多数的自动化设备表面都是由各类金属材质构成的,由于在浑浊的工业环境中设备长期与空气中的物质及各种工业杂质产生接触,就会使得高强度的钢表面出现腐蚀、锈蚀等现象。当金属材质发生腐蚀就会导致其表面机理出现损伤甚至断裂及其他损坏现象,从而引起巨大的安全隐患和经济损失。所以对设备表面出现的腐蚀现象及时进行清理是很有必要的。
文献[1]采用一种基于微米颗粒的硅表面杂质的清理方法,该方法通过观察水呈现液态膜形式时,利用低功率激光可以有效去除表面的微米颗粒。此方法所用功耗较低、时间较快,但是在清洗除锈完成后表面易出现液膜水质的残留物,从而导致产生频繁性重复腐蚀的现象。文献[2]是根据一种双重激光扫描的腐蚀去除方法,分析发现在前一清洗激光进行有效除锈后,后一激光再进行二次除锈可以消除清洗残留,避免出现二次腐蚀现象。该方法虽然去除效率及质量较高,但是容易忽略腐蚀区域内原有金属元素的因素,导致进行高强度的二次清洗后,会破坏设备表面的机理,降低使用寿命,增加损耗。
本文基于上述问题,提出一种基于空间插补的激光清洗技术,利用该方法可以有效寻找模拟空间内的最佳三点值,并选择最优直线,减少激光线段间的时间耗用,提高清洗效率。并且还能有效控制激光功率,在高效清洗的同时还能避免金属表面机理被破坏。仿真实验证明,本文方法对腐蚀区域的清洗效果较高、清洗效率较高,并且对金属表面损坏程度较小,能够实现有效清洗。
1 自动化设备外表面腐蚀区域程度判定
一般情况下,自动化设备外表面出现腐蚀区域,几乎都是因为其表面与空气中的一些介质接触产生了化学反应,从而使得表面的金属出现腐蚀现象[3]。这时,就需要对腐蚀区域内的元素和物质进行科学判定,这样才能根据不同的腐蚀程度实现对症清洗,保证实现有效去除,并且不会造成金属表面或零件的损伤。本文通过一种判定公式对污染物的吸附力[4]、重力以及双静电层[5]进行判断,为后续的激光技术清洗提供有利条件。
通常来看,一般金属表面腐蚀区域的污染物都是依靠吸附力、双静电层和毛细力[6]为基础才能附着在物体上,其具体吸附示意如图1所示。

图1 三种基本的附着示意图
微米污染物主要是依靠附着力才能在金属表面进行腐蚀和污染,其在杂质中的表现形式是一种直径为d的球状物体,那么其吸附力表现公式为
FV≈hd/16πz2
(1)
式中:h为与金属材质有关的常数;z为小球与金属表面的微观距离,考虑到小球会发生畸变的情况,所以将原有数值增加一定比例。
而毛细力一般是指在小球与金属表面产生的空隙中所有微小颗粒的凝聚,其数值大小的具体表达公式就为
F0=2πγd
(2)
式中:γ为颗粒的凝聚单位。基于上述计算公式就可计算得出其毛细力和物质吸附力的具体数值,通过此数值判断自动化设备表面腐蚀区域的污染物与材质之间的关系,提高清洗效率减少相应损耗,还能避免出现过度清洗造成损伤。
2 基于空间插补法的激光清洗技术
激光清洗技术主要是依靠一种水体形成的冷凝法,清洗时在物体表面与半导体硅表面之间产生一层几微米厚度的水膜,再借助激光的脉冲功率高强度照射其表面。由于长时间的高强照射使得水膜会不定时发生大量蒸发,借此冲击表面腐蚀区域的微粒,可以有效清除其中氧元素和其他杂质。
掌握激光清洗技术的关键在于需要时刻把握其物质表面与介质膜之间的关系。由于激光清洗是一项高强度高热量的爆炸式工作,所以必须在过程中实时掌握温度随空间距离以及时间变化的情况,一旦发现温度异常就需立即停止,不然不发生不可控的汽化从而导致表面材质发生损伤。基于这种方法,可以对自动装置的表面材料进行具体分析,并研究介质膜与表面材质的关系,从而减少消耗、合理控制温度和时间,达到高效清洗的目的,其激光清洗技术模型如图2所示。

图2 激光清洗技术模型
2.1 算法特征
本文采用一种基于最小二乘积的空间插补算法,该算法可以保证激光技术的扫描精度,并增强工作效率降低设备损耗,保证基于激光清洗技术过程的有效性和稳定性。
目前多数的激光清洗技术都为平面激光清洗,比如振动式的水洗加工。而对于较为单一的曲线插补现状,本文提出一种利用最小二乘积算法的插补方式,该算法巧妙地根据拟合空间中任意三点到设立终点坐标的距离关系,从而取得一条关于空间向量的直线,用这条直线代替原始空间中的所有直线,就可以取得最优线段距离,较少耗用时间、增强扫描效率。
设空间内的所有计算点为A、B、C、D、E、F、G、H、I、J、K、L、M、N、O、P、Q、R、S,通过这些计算点的坐标并寻找其中任意三点的坐标系数,把原始的两点连线用此类AD、DG、GI、IL、LN最短线段替代,这样可以在一定程度上降低空间内直线的计算数量,提升扫描速度,增强整体效率,其任意三点的空间附着示意如图3所示。
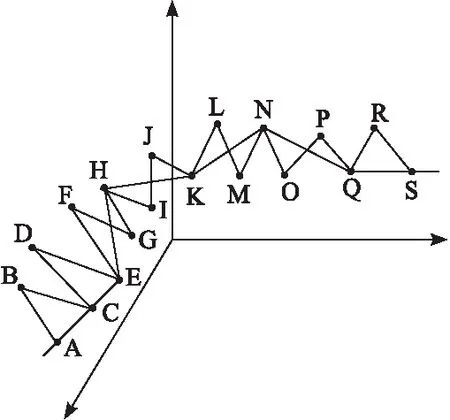
图3 任意三点空间插补示意图
2.2 基于最小二乘积的空间插补过程
通过上述过程的曲线插补特征计算,再根据最小量化误差数值的平方为基准选择一组与最佳函数序列最为匹配的数据样本。
最小二乘积方法是最为合适且最简便的空间插补算法之一,因其可以通过三点间的最优曲线求值取得一些不能轻易得知的真实数值,这样对比其他算法其占有一定优势。首先,设三点间的误差平方和的数值为最小数值,且此数值为正整数,再根据通常算法下的曲线拟合方法将三点间的空间曲线进行拟合,其具体表示为
(3)
此时三点坐标空间内的直线方程公式通常可以表示为
(4)
式中:x0、y0、z0分别为空间内的三点间的三维向量坐标值;m1、m2、m3则分别为空间内任意一组直线方向上的向量,这样就可以用x、y、z三点坐标,来表示空间的三点间的任意直线方程表达公式为
(5)
(6)
一般情况下,大多数都会采用两个非平行的平面进行相交的形式来表示空间内的任意直线,所以空间内的平面的表达公式为
Aix+Biy+Ciz+Di=0
(7)
式中:A、B、C分别为任意平面内线段的法向量。这样就可以通过式(3)和式(4)分解变形得出两个平面相交时线段的法向量[7]数值为n1={10-a}、n2=0{11-c},根据这两种法向量的表达取值范围得出空间内直线的任意方向的向量值:
(8)
根据式(7)和式(8)依次计算可以得出Δx和Δy的具体数值,再对这两个数值进行偏导令全部偏导数值[8]都为0:
∑2×[xi-(azi+b)]×(-1)=0
(9)
∑2×[xi-(azi+b)]×(-zi)=0
(10)
∑2×[yi-(czi+d)]×(-zi)=0
(11)
∑2×[yi-(czi+d)]×(-1)=0
(12)
根据上述公式法则就可以依次求出对应的a、b、c、d的具体数值。根据空间内各点之间的直线距离公式就可计算得出任意点到任意直线的距离,其具体计算公式如下:
(13)
将上述过程求解得出的A、B、C、D以及a、b、c、d各数值代入到式(13)中,最终求得d的数值,并且找到空间内任意点到拟合空间内任意直线的距离关系。
由上述过程可知,通过拟合空间内两个信息数据点就可以确定拟合直线的实时系数,从而就可确定拟合空间内直线的表达关系式,以此为基础,就可计算出任意数据点到任意直线间的时效距离。这时如果计算下一点时出现超出范围的条件误差δ,则就可以下一点为基准进行重新计算,将第二个点的坐标作为终点坐标,减少计算误差。至此,完成空间内所有坐标点到拟合曲线[9]的距离计算,其具体流程如图4所示。
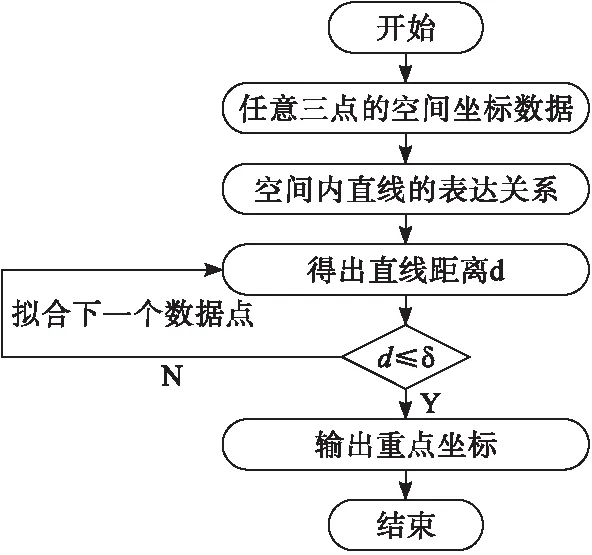
图4 计算流程及具体框架
利用最小二乘积法好处在于可以在大量已知的数据中进行三维点[10]的数据计算,这样就能保证在空间拟合过程时出现线段误差影响插补精准性。并且在进行激光清洗技术时往往都需要空间上曲面的特性[11]来加速激光插补过程,保证清洗质量以及效率。
本文采取上述过程中的最小二乘积算法实现空间插补过程,可以有效实现所有任意基于三点数据的向量空间线段拟合,如图5所示。

图5 基于最小二乘积的直线拟合方法
其中,在可衡量的误差范围以内,所有临近点之间的最短直线就可以由拟合空间[12]中设立的直线所替代,在一定程度上减少直线基数,降低计算误差,使得激光清洗技术能够快速且高质量地完成。
3 仿真实验
3.1 实验背景
为有效研究本文提出的基于自动化设备外表面腐蚀区域激光清洗技术的具体实验效果,将采取电机功率为300~800 W的自动化机器作为实验设备,其表面腐蚀区域内元素的具体参数如表1所示。
激光清洗功能对应的激光离焦量参数为3.8 mm,平均每秒的扫描速率是600 mm/min,竖直方向的扫描路径是30 mm,横向的扫描路径为40 mm,金属表面原始元素的密度值分别为锌元素7.14 g/cm3、铁元素7.86 g/cm3、汞元素13.59 g/cm3、铜元素8.9 g/cm3。
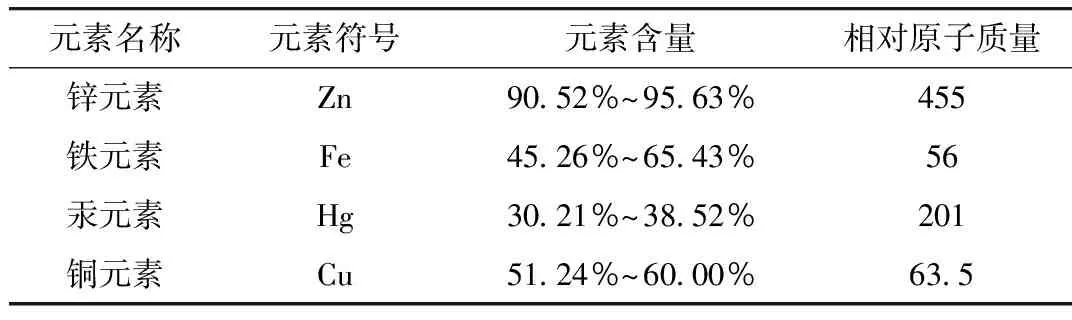
表1 金属表面元素的具体参数
3.2 表面腐蚀层氧元素去除对比分析
腐蚀区域中的大致成分主要为氧化物,根据采集的氧化物元素含量的实时变化,就能够直观、准确地观察出腐蚀区域中污染物的清洗程度。所以本文将通过能谱数据分析法对不用清洗技术下的腐蚀样本中的氧化物含量做出有效判定与分析,保证实验的直观性和真实性。其文献[1]、文献[2]与本文共同进行的腐蚀区域清洗效果如图6所示。

图6 氧元素含量去除效果
从图6中可以看出,基于文献[1]清洗方法下的金属表面腐蚀区域内的氧元素含量并未出现明显的减少。相比之下,文献[2]的氧元素去除效果比文献[1]优异许多,但是在清洗功率达到300 W时出现了待滞现象,去除效率并未随着功率的增强而增强,是处于一种停滞不前的状态,这就说明当清洗功率与实际效果已经出现饱和状态,继续进行只会导致表面机理出现破坏,影响设备安全。出现这种现象的主要原因就是没有在技术清洗前,对表面腐蚀区域进行附着物判断,从而导致出现清洗饱和的现象,影响整体清洗效率以及质量。
反观本文基于激光清洗技术的实验效果,平均氧元素的去除率含量达到了50%左右,这足以说明,本文方法对腐蚀区域清洗的效果较好,且整体的清洗过程较为平稳,曲线一直呈稳定的上升趋势并未出现饱和、停滞等现象,这主要是因为,本文利用对腐蚀区域内的吸附力、重力以及静电层进行科学判定,并根据不同的腐蚀程度实现对症清洗,在不会造成金属表面或零件的损伤的同时还能保证实现氧元素的有效去除,增强清洗效率改善耗用时间。
3.3 表面机理破坏程度分析
一般情况下,想要实现腐蚀污浊物的彻底清除就必须采取高功率、高强度的清洗方法,但此类方法不易控制清洗的最优频率从而导致金属表面的机理出现破损现象。所以本文将通过对比三种方法下金属表面密度数值的变化状态,来判定清洗技术对原始机理的破坏程度,并且还会比较清洗后原有金属元素的保留含量进一步判定实验结果的优异性。
其中,能谱值表示脉冲信号随能量分布的曲线,可以表示为激光清洗信号文献[1]和文献[2]方法以及本文对自动化设备采取清洗、清洗功率为500 W,结果如图7和表2所示。

图7 三种方法下元素密度变化
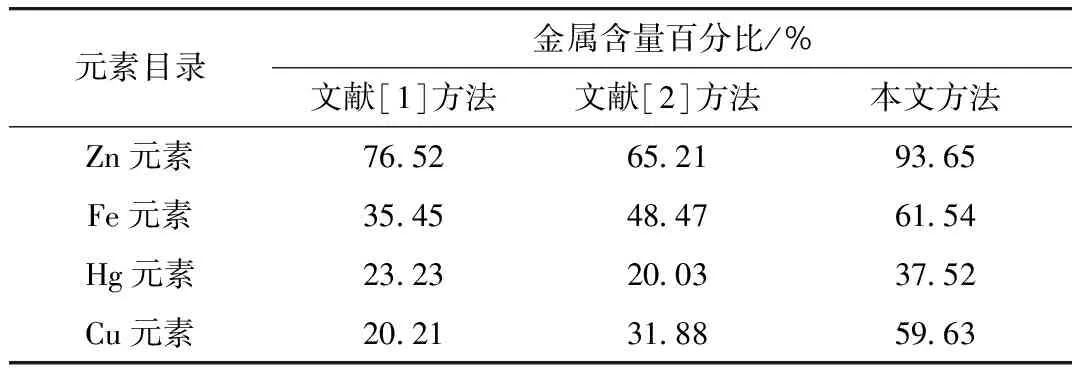
表2 清理前后表面金属含量对比
从图7中可以看出,基于本文方法清理后的自动化设备各类元素的密度数值与原数值相比未出现较大差异,并且根据表2中的机器表面各金属元素含量与清理前也没有太大的变化,这就说明本文对于清洗技术的功率设置的度量把握较好,在能保证有效清洗的同时还不会破坏金属机理,这主要是因为在利用激光清洗技术时引入了空间插补的机制,通过拟合空间的方式让激光曲线找到最为合适的三种空间基点,实现基于最短直线的激光进程,这样不仅能提高清洗效率还会在一定程度上抑制清洗功率及频率,能够较好地把握清洗度量,不会造成元素密度的破坏。
4 结 论
本文基于自动化设备外表面腐蚀区域激光清洗技术进行研究分析得出以下结论:
(1)通过计算得出其自动化设备表面材质的毛细力与吸附力的具体数值,以此为判断依据不仅可以减少响应时间与材料损耗、提高清洗效率,还能避免出现过度损伤。
(2)本文采取的基于最小二乘积的空间插补算法,可使得激光清洗技术具有的高功率、高频率特性得到高效发挥,有效改善激光扫描的精度并增强整体工作效率、降低设备损耗,确保整个清洗过程的有效性和稳定性。
(3)仿真实验证明,基于所提方法对自动化设备腐蚀区域的清洗效果优异,可以有效去除表面氧元素与其他杂质,保证清洗后材质表面的机理、形貌、纹理等不会出现破坏现象,且不会留下腐蚀坑。本系统在各方面来看都具有较高的应用价值。

