基于“主题单元”理念的教学设计展示——以“基本初等函数的导数公式及导数的运算法则”为例

⦿广东省东莞市东莞中学

崔吉平

1 “主题单元”教学设计的内涵

主题单元教学，也叫主题式授课，是指把课时教学设计融入主题单元教学设计中的一种授课模式.有别于传统教学，主题单元教学就是要在课时教学设计之前，先进行本单元的教学设计，对本单元内容及其蕴含的数学思想和方法、着重培养的学科核心素养、要达成的教学目标等作出全面分析，然后按照知识的发生发展过程、学生的认知过程分解到具体课时.主题单元教学的内容不拘一格，既可以是课本章节内容，也可以是其他的通过梳理整合的教学材料，操作性强，灵活性好，是发展“四基”、提高“四能”的重要载体，是提升核心素养，践行新课程标准(2017年版)的绝佳路径.本文以《选修2-2》中“基本初等函数的导数公式及导数的运算法则(第1课时)”为例，向读者展示基于“主题单元”理念的一篇教学设计，望能起到抛砖引玉的作用.

2 教学设计展示

2.1 单元目标及解析

(1)通过分析变化率问题，了解平均变化率和瞬时变化率，了解两者的关系，理解导数概念的本质——导数就是瞬时变化率；

(2)能借助《几何画板》理解函数切线与割线的关系，从中感受极限思想，并能指出导数的几何意义；

(4)能通过研究函数图象切线去分析初等函数的导数公式，并能熟练掌握导数公式；

(5)理解导数的运算法则及复合函数的导数公式，并能运用公式及法则求简单函数的导数；

(6)会利用导数公式及运算法则求曲线的切线方程和瞬时变化率.

2.2 课时目标及重难点

(1)教学目标：能熟记基本初等函数的导数公式和导数运算法则，能利用基本初等函数的导数公式和运算法则求简单函数的导数，能求曲线在某点处的切线方程.

(2)教学重点：八个基本初等函数的导数公式和导数运算法则的理解、记忆与应用.

(3)教学难点：①理解函数y=sinx，y=cosx，y=ax，y=logax的导数公式.(a>0,且a≠1.)

②导数运算法则(乘除)

[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x),

的记忆与应用.

2.3课时教学过程设计

2.3.1 问题引入，激发兴趣

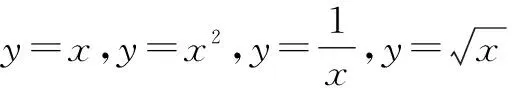
追问1-1：你能从中得出幂函数f(x)=xα(α∈Q,且α≠0)的导数公式吗？

生：f(x)=x，则f′(x)=1；

f(x)=x2，则f′(x)=2x；

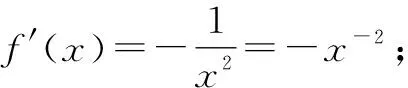
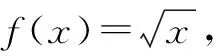
由此归纳可得，若f(x)=xα(α为有理数)，则f′(x)=α·xα-1.

设计意图：通过对四个已知幂函数的导数作出归纳，从特殊到一般得到幂函数的导数公式，学生积极参与，信心高涨，学习热情被迅速点燃.

2.3.2 由形到数，发现公式

问题2除了利用导数定义，我们如何利用函数y=f(x)的图象去研究它的导数？

引导学生回忆导数的几何意义，通过讨论达成共识：要研究函数的导数，只需要研究函数图象的切线斜率值的变化情况.

设计意图：加强学生对导数本质的理解，为下面的教学奠定逻辑基础.

问题3现在来研究三角函数的导数公式，请在学案上画出函数f(x)=sinx，x∈[-2π，2π]的图象，观察其切线斜率值的变化，你有什么发现？

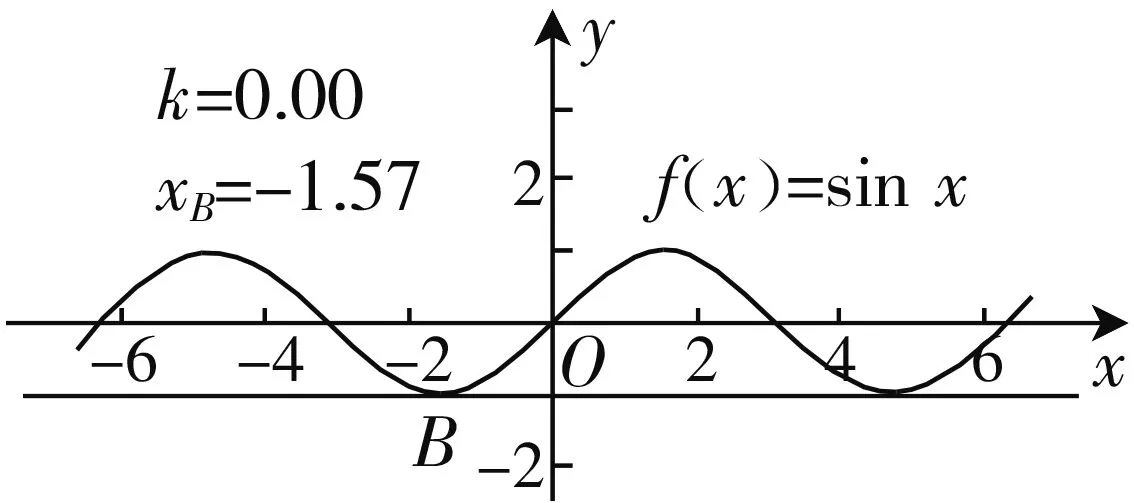
图1

生：如图1所示，观察出切线斜率的值呈现周期性变化，其范围在[-1，1].

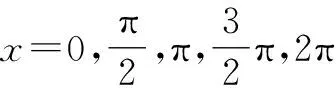
追问3-1：猜想正弦函数、余弦函数的导数.

学生活动：画图(图2)，独立思考后相互讨论，得到“正弦函数的导数是余弦函数，余弦函数的导数是正弦函数的相反数”.

图2

设计意图：通过作图及《几何画板》演示，巧妙缩短了教学内容与学生的心理距离，加深学生对三角函数导数公式的理解与记忆，培养了直观想象与逻辑推理素养.

问题4你如何快速记牢八个导数公式？

学生活动：同学们发言踊跃，能说出八个导数公式分别是常值函数、幂函数、三角函数(两个)，指数函数(两个)，对数函数(两个)，第6个公式是第5个公式的特殊化，第8个公式是第7个公式的特殊化.

设计意图：课堂气氛轻松愉悦，学生反响热烈，教学效果好.

2.3.3 法则探究，活学活用

问题5你会求课本第3页问题2中的函数h(t)=-4.9t2+6.5t+10的导数吗？这里主要涉及到导数的哪些运算法则？

生：导数的加法和乘法的运算法则.

两个函数f(x)与g(x)的和(或差)的导数法则：[f(x)±g(x)]′=f′(x)±g′(x).(教师板书)

追问5-1：[f(x)g(x)]′=f′(x)·g′(x)成立吗？

教师活动：表扬学生，给出法则[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x).

追问5-2：如果函数g(x)=c(c为非零常数)，你能得到什么结果？

生：[cf(x)]′=cf′(x).

生：分母是原先分母的平方，分子是个差值.

生：分子是f′(x)g(x)-f(x)g′(x).

设计意图：利用课本例子指出学习导数运算法则的必要性，处理巧妙，然后通过找反例、分析结构加深学生对导数运算法则的理解和记忆.

2.3.4 课后训练，巩固提高

(1)求下列函数的导数：

①y=(x-1)3； ②y=xn2x；

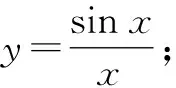
设计意图：第(1)题是检测学生对基本初等函数的导数公式及导数的运算法则的掌握情况，第(2)题主要是检测学生导数公式的运算素养水平.

3 总结与反思

本文是2020年11月份作者在广东省惠州市举办的华南师范大学教育服务合作项目——高中数学“同课异构”教研活动中，上的一节示范课的教学设计的修改稿.整个课堂紧扣主题单元设计的要求，通过问题串的设置与解决促使学生由表及里掌握导数公式与运算法则，把数学知识的教学、数学思维的引导、数学能力的提升融为一体，有一定的启发性和参考性.美中不足的是两个函数的商的导数法则学生理解起来还有些困难，需要我们更细致地设计和引导帮助学生顺利过关，真正使学生的数学学科核心素养落到实处，生根发芽，茁壮成才.