近63a黄河源区气温变化规律分析

蓝云龙，黎 曙，关铜垒，李 霞，徐东坡，刘佳嘉

(1.黄河水利委员会西宁水文水资源勘测局，西宁，810008；2.中国水利水电科学研究院，北京，100038；3.黄河勘测规划设计研究院有限公司，郑州，450003)

1 前言

近年来，在全球变暖的大背景下，气候变化及其影响是关注研究的热点[1]。黄河源区作为气候变化敏感的区域，其气候变化问题一直受到国内众多学者的关注和研究，郝振纯等[2]指出，自1954-2007年黄河源区平均气温呈现上升趋势；易湘生等[1]基于滑动平均、线性倾向估计、样条函数插值和MK检验等方法对黄河源区1961-2010年间气温变化进行分析，分析表明，黄河源区年均气温呈现波动上升趋势，且冬季在进入21世纪后增温极为显著；杨昭明等[3]基于黄河源区9个气象站数据分析了黄河源区近57a的气温数据，研究表明，黄河源区近57a年均气温、年均最大气温、年均最低气温均呈现显著上升趋势；孟宪红等[4]基于黄河源区近50～60年气候变化事实，指出黄河源区气温呈现显著升温趋势，且自西向东升温速率逐渐增加；王栋等[5]分析黄河源区1961-2016年年均气温变化特征，研究表明，黄河源区年均气温呈现为显著上升趋势，突变年份为1997年。

总体来看，黄河源区气候变化主要呈现为气温不断升高的趋势[2-6]。但是，由于不同的学者研究时所选的气象站点不同、时间序列不一、分析方法不同、研究分区划分单一等原因，使得对于黄河源区的气候变化问题的认识不够深入。因此，为更好地分析探究黄河源区的气候变化规律，本文根据黄河源区1956-2018年间63a的长时间序列气温数据，分别对黄河源区及其三个分区，从周期性、突变性和趋势性三方面进行详细分析，旨在为黄河源区的水资源、生态环境保护提供参考。

2 研究区及数据

黄河源区(唐乃亥水文站以上区域)位于青藏高原中部，流域面积达12.2km2，属于典型的内陆高原气候，寒冷干燥，日夜温差较大，冬冷夏凉，且辐射强，蒸发大。为更好地分析黄河源区气温变化特征，将黄河源区划分为三个区间——黄河源头区、黄河沿-玛曲、玛曲-唐乃亥[7-8]，如图1所示，分别对黄河源区及其三个分区进行气温变化特征分析。

本文选择黄河源区及周边14个国家气象站点(见图1)1956-2018年逐日气温数据资料，采用修正反距离加权平方法[9]和泰森多边形法[10-11]对气温数据进行空间插值，对个别气象站点缺测数据，采用其他站点相应日期数据进行插值，由此得到黄河源区及其三个分区的气温数据。

图1 黄河源区研究分区及气象站点空间分布

3 研究方法

3.1 Mann-Kendall趋势性分析法

Mann-Kendall趋势性分析法，通常称之为MK检验法，它作为一种非参数检验，利用样本数据计算的结果，表现样本数据的趋势性变化以及显著性突变，被大量学者广泛用于水文领域长时间序列的趋势性与突变性分析[12]。对于MK法而言，初始假设H0所代表的数据集X的样本为独立且同分布，且不存在趋势性，而其备用选择的假设H1表示数据集X中存在有且只有一个单调的趋势性变化。该方法所构造的统计量公式可表示如下：

(1)

其中，

(2)

式中，xj和xi为样本的数据值，n为样本容量，参数sgn(xi-xj)将根据xi-xj计算结果的正负分别表示为1、0和-1。如果计算结果-Z1-α/2≤Zc≤Z1-α/2，则表示初始假设H0为真。同时MK法还有另一个量化指标——倾斜度β，它可以用来表示数据的单调趋势，β的计算公式表示如下：

(3)

式中，10时，则表示上升的趋势，如果β>0且大于相应置信度，则表示具有显著性上升趋势，否则为不显著的上升趋势；同理，当β<0时，则表示下降的趋势，如果β<0且小于相应置信度，则表示具有显著性下降趋势，否则为不显著的下降趋势。

3.2 Pettitt突变性分析法

Pettitt突变检验法[13]作为非参数检验方法的一种，通常称之为P突变，该方法简单有效，对突变点的识别准确度高，被广泛应用于确定长时间序列数据中的突变点，得到长时间序列数据中的突变年份。P突变的检验统计量为Ut，N，其表达式如下：

(4)

根据上述公式计算所得的结果Ut，N可计算如下指标：

Kt，N=max|Ut，N|，(1≤t≤N)

(5)

p=2exp[-6Kt，N2/(N3+N2)]

(6)

通常情况下，当p≤0.05时，认为数据中存在突变点。

3.3 小波周期性分析法

小波分析法主要描述水文各要素之间的相互关系以及存在的潜在规律，通常用于降水、径流等要素的分析。众多学者研究了多种小波基函数的适用性，大家一致认为Morlet小波是使用最广泛、效果最明显、优势最突出的一个小波基函数，因此选择该函数作为本文小波分析中的基函数[14]。Morlet函数的表达式为：

(7)

Morlet小波的傅里叶变换为：

(8)

其中i为虚数，t为时间，ω0、ω为常数。

4 结果与讨论

4.1 趋势性分析结果

采用上述MK检验法对黄河源区1956-2018年连续63a年均气温数据进行分析，其变化过程线如图2(a)所示，根据MK趋势检验结果，其中检验指标量Zc为5.332，该值大于0.05显著性水平下的临界值1.96，同时气温变化过程线的倾斜度β为0.0258，该值大于0，因此认为黄河源区1956-2018年63a间气温呈现显著性持续升温趋势。另外分别对其三个分区的年均气温进行MK趋势检验，各分区年均气温变化过程线如图2(b-d)所示，黄河源头区MK检验统计量Zc值为5.9252，大于0.05显著性水平下的临界值1.96，且倾斜度β为0.0345>0，故黄河源头区气温呈现显著性的升温趋势；黄河沿-玛曲MK检验统计量Zc值为5.937，大于0.05显著性水平下的临界值1.96，且倾斜度β为0.0314>0，故黄河沿-玛曲气温呈现显著性的升温趋势；玛曲-唐乃亥MK检验统计量Zc值为3.0308，大于0.05显著性水平下的临界值1.96，且倾斜度β为0.13>0，故玛曲-唐乃亥气温呈现显著性的升温趋势。综上表明，黄河源区和其三个分区的气温呈现一致性的升温趋势。

从气温过程线和MK检验指标中的倾斜度β可知，黄河源区气温平均每10年增长0.258℃。三个分区中，黄河源头区的气温增长速率最高，平均每10年增长0.345℃；黄河沿-玛曲的气温增长速率次之，平均每10年增长0.314℃；玛曲-唐乃亥的气温增长速率最低，平均每10年增长0.13℃。另外，黄河源区及其三个分区中，黄河源头区年均气温最低，多年年均气温均在-4℃以下，这与该分区的海拔最高有直接关系。

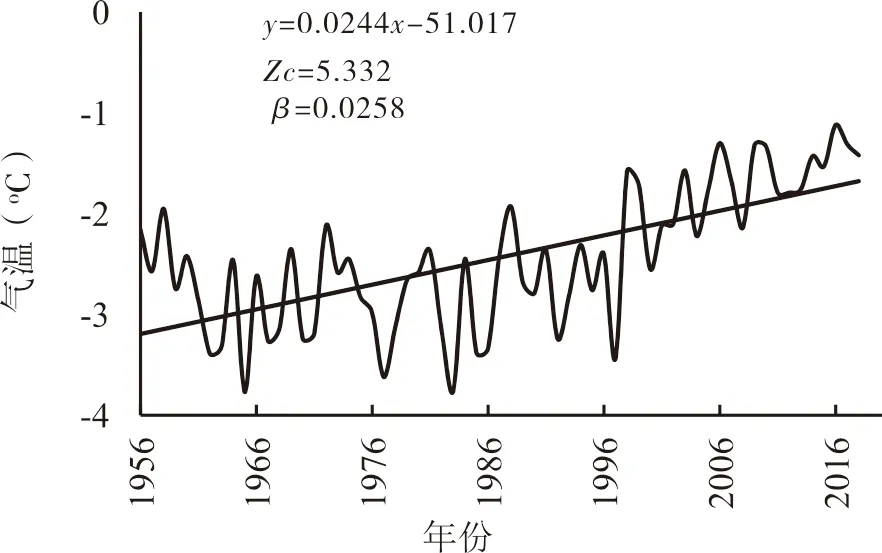
(a)黄河源区

(b)黄河源头区

(c)黄河沿-玛曲

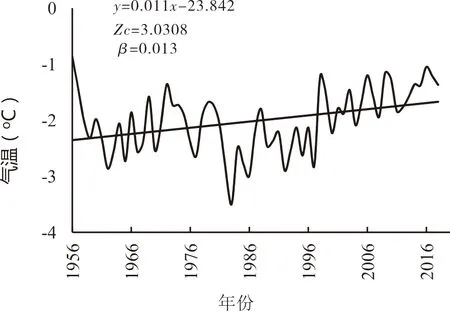
(d)玛曲-唐乃亥 图2 黄河源区1956-2018年年均气温变化趋势

4.2 突变性分析结果

采用Pettitt突变检验法对黄河源区1956-2018年年均气温进行分析，检验结果如图3(a)所示，选择0.05和0.01显著性水平时，Pettitt突变检验指标p值为0.0016×10-4<0.05且0.0016×10-4<0.01，黄河源区气温存在显著突变点，根据检验统计量最大值可确定突变年份为1997年。再对黄河源区三个分区分别进行Pettitt突变分析，检验结果如图3(b-d)所示，同样选择0.05和0.01显著性水平，得到黄河源头区Pettitt突变检验指标p值为0.0011×10-4<0.05且0.0011×10-4<0.01，故黄河源头区气温存在显著突变点，根据检验统计量最大值可确定突变年份，并且突变年份与黄河源区的突变年份一致，均为1997年；黄河沿-玛曲Pettitt突变检验p值为0.00125×10-4<0.05且0.00125×10-4<0.01，故黄河沿-玛曲气温存在显著突变点，根据检验统计量最大值可确定突变年份，突变年份与黄河源区突变年份一致，均为1997年；玛曲-唐乃亥Pettitt突变检验指标p值为0.0077×10-2<0.05且0.0077×10-2<0.01，故玛曲-唐乃亥气温存在显著突变点，根据检验统计量最大值可确定突变年份，突变年份与黄河源区突变年份一致，均为1997年。

综上表明，1956-2018年黄河源区与其三个分区的气温均存在突变点，突变年份均为1997年。

(a)黄河源区

(b)黄河源头区

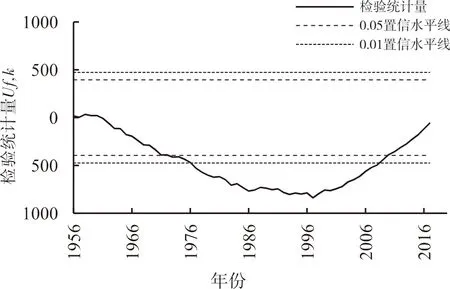
(c)黄河沿-玛曲

(d)玛曲-唐乃亥 图3 黄河源区1956-2018年年均气温突变检验结果

4.3 周期性分析结果

对黄河源区1956-2018年年均气温进行小波分析研究其周期性，小波方差图如图4(a)所示。从图中可知，黄河源区气温小波方差图中同时存在三个峰值，即存在三个主周期。分别对第一、第二、第三主周期绘制相对应的小波实部过程线图，如图4(b-d)所示，则确定1956-2018年黄河源区年均气温第一主周期为27a左右，第二主周期为7a左右，第三主周期为3a左右。

(a)黄河源区

(b)一级三周期

(c)二级主周期

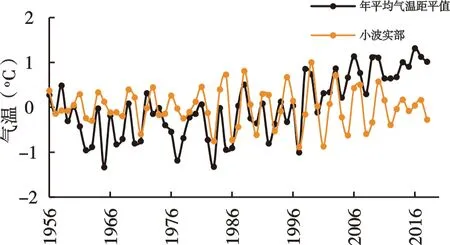
(d)三级主周期 图4 1956-2018年黄河源区年均气温小波方差及小波实部

对黄河源头区1956-2018年年均气温进行小波分析研究其周期性，小波方差图如图5(a)所示。从图中可知，黄河源区气温小波方差图中同时存在三个峰值，即存在三个主周期。分别对第一、第二、第三主周期绘制相对应的小波实部过程线图，如图5(b-d)所示，则确定1956-2018年黄河源头区年均气温第一主周期为27a左右，第二主周期为8a左右，第三主周期为3a左右。

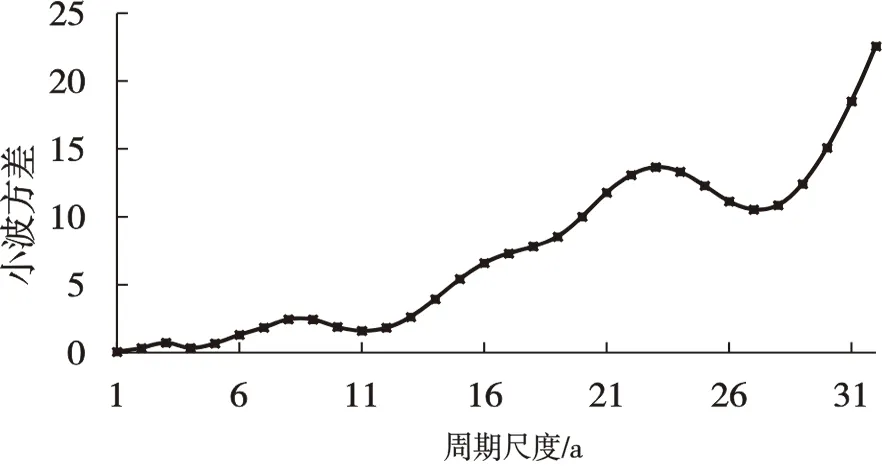
(a)黄河源区

(b)一级主周期

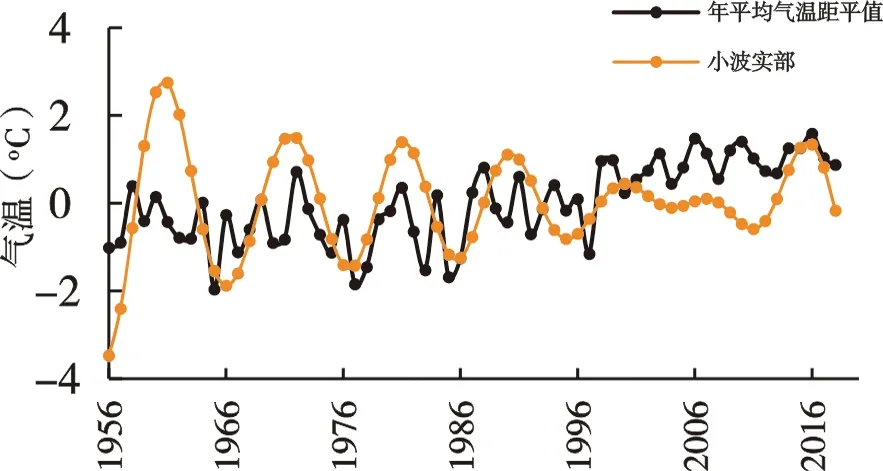
(c)二级主周期

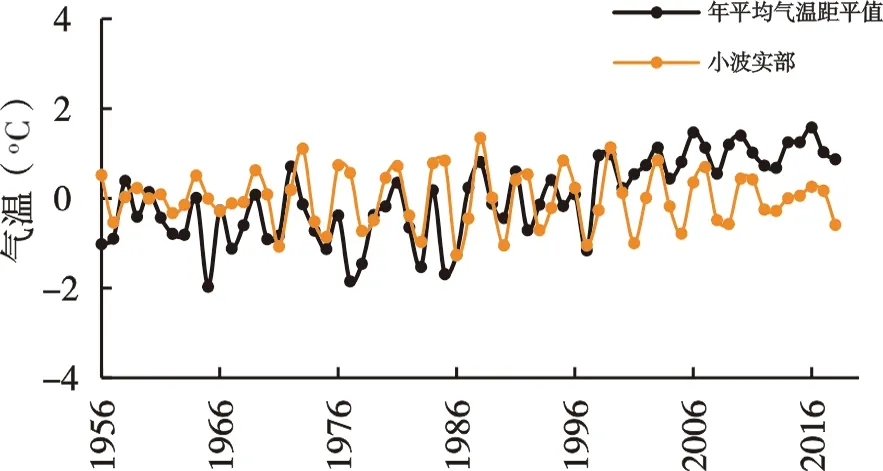
(d)三级主周期 图5 1956-2018年黄河源头区年均气温小波方差和小波实部

对黄河沿-玛曲1956-2018年年均气温进行小波分析研究其周期性，小波方差图如图6(a)所示。从图中可知，黄河源区气温小波方差图拥有两个峰值，即存在两个主周期。分别对第一、第二主周期绘制相对应的小波实部过程线图，如图6(b-c)所示，则确定1956-2018年黄河沿-玛曲年均气温第一主周期为7a左右，第二主周期为3a左右。

(a)黄河沿-玛曲

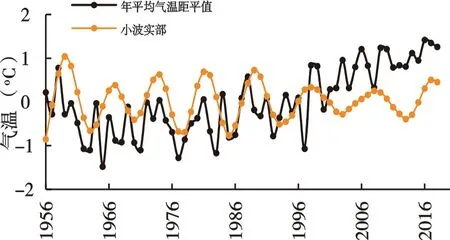
(b)一级主周期

(c)二级主周期 图6 1956-2018年黄河沿-玛曲年均气温小波方差和小波实部

对玛曲-唐乃亥1956-2018年年均气温进行小波分析研究其周期性，小波方差图如图7(a)所示。从图中可知，玛曲-唐乃亥气温的小波方差图中拥有三个峰值，即存在三个主周期。分别对第一、第二、第三主周期绘制相对应的小波实部过程线图，如图7(b-d)所示，则确定1956-2018年玛曲-唐乃亥年均气温第一主周期为27a左右，第二主周期为8a左右，第三主周期为3a左右。

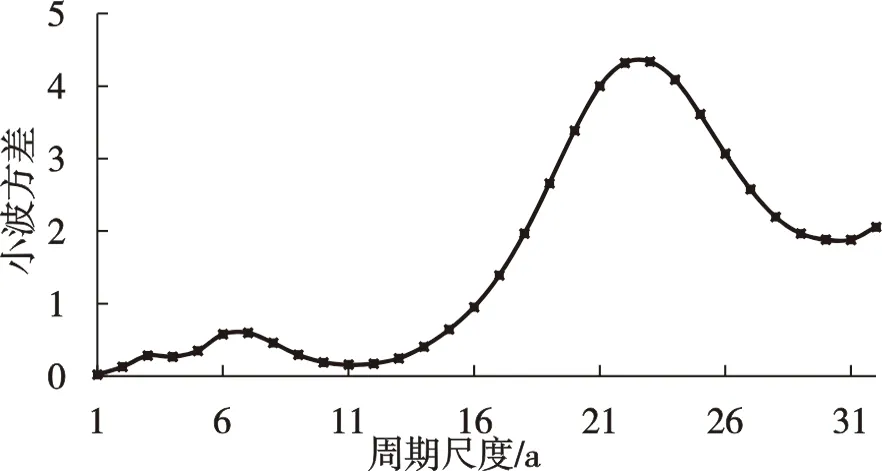
(a)玛曲-唐乃亥

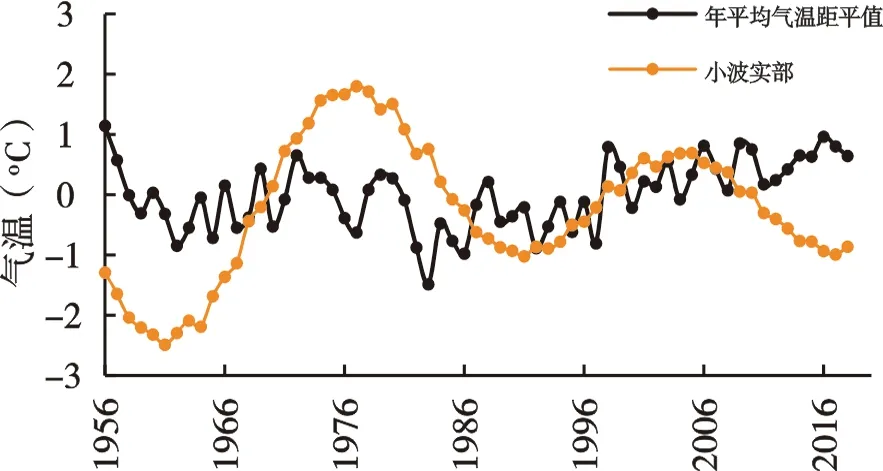
(b)一级主周期

(c)二级主周期

(d)三级主周期 图7 1956-2018年玛曲-唐乃亥年均气温小波方差和小波实部

4.4 讨论

1956-2018年黄河源区多年年均气温为-2.436℃，黄河源头区多年年均气温为-4.852℃，黄河沿-玛曲多年年均气温为-1.881℃，玛曲-唐乃亥多年年均气温为-2.014℃，黄河源头区年均气温最低，主要原因为该分区海拔较高。黄河源区及其三个分区年均气温均呈现显著升温趋势，分析其原因，这与全球变暖大趋势一致，三个分区的气温增幅差异应该与各分区海拔高度以及下垫面差异有关。

1956-2018年黄河源区及其三个分区年均气温均呈现显著性升温趋势，该结果与易湘生[1]、杨昭明[3]、孟宪红[4]、王栋[5]等结论一致；1956-2018年黄河源区及其三个分区年均气温具有显著突变点，突变年份为1997年，该结果与杨昭明[3]、王栋[5]等结论一致；1956-2018年黄河源区及其三个分区年均气温具有明显周期性，该结果与王栋[5]结果有出入，可能与选择数据系列年份、站点数量及位置有关。

5 结论

(1)从1956-2018年年均气温来看，黄河源区及其三个分区(黄河源头区、黄河沿-玛曲、玛曲-唐乃亥)气温均呈现显著性增长趋势，且黄河源头区气温增长速率最高，平均每10年增长0.345℃；

(2)1956-2018年间，黄河源区及三个分区(黄河源头区、黄河沿-玛曲、玛曲-唐乃亥)年均气温均存在显著突变点，且突变年份一致，突变年份均为1997年；

(3)黄河源区及其两个分区(黄河沿-玛曲、玛曲-唐乃亥)均存在三个主周期，且一级主周期的周期均为27-28a左右，二级主周期的周期为7-8a左右，三级主周期的周期为3a左右；黄河源头区有两个主周期，第一主周期为7a左右，第二主周期为3a左右。