基于风力发电机组叶根载荷变换桨距角反馈线性化的独立变桨控制策略研究
任小勇
(1.酒泉职业技术学院,甘肃 酒泉 735000;2.兰州理工大学,甘肃 兰州 730000)
1 基于叶片根部载荷变换桨距角反馈线性化变桨距控制原理
1.1 控制思想
叶轮在旋转过程中,会受到各种力的影响,受力非常复杂,所受到的各种载荷通过叶根作用到了轮毂,一般情况下,风机受到的载荷有两种,分别是动态载荷和静态载荷。 静态特性的载荷变化比较缓慢或者不变化,对风力发电机组的影响较小,可以忽略不计,在风机设计和制造的过程中,可以通过对风机结构的优化等方式来消除静态载荷。 运行中的风力发电机,叶片受到自然风、风切变、突变的风等会产生动态载荷,动态特性的载荷随时间变化,如果不能及时处理,就会影响风力发电机的稳定性和使用寿命,因此在风力发电机组变桨距控制中,考虑载荷对风机的影响时,只需考虑风机的动态载荷[1]。
只要叶片转动,就会受到气流的作用产生动态载荷,传递到轮毂上,对轮毂产生影响。 在设计变桨距控制策略的时候,一定要考虑动态载荷。 风机在运行的过程中受到的载荷分为两类,一类是风机转动时的气动转矩。 气动转矩主要就是带动发电机转动,气动转矩会受到风剪切、塔影效应、尾流的影响,叶轮波动,发电机电磁转矩作用等,会对风力发电机组的传动系统产生扭曲和震动,影响风力发电机的功率输出。 风机的动态载荷分为两部分,一是在气流作用下产生的气动转矩,二是因气流影响产生的不平衡载荷[2]。
叶片的动态载荷主要表现形式是叶片的拍打和叶片的挥舞,叶片的拍打主要是在旋转过程中的振动,与风剪切和旋转湍流有关,叶片的挥舞主要是在旋转过程中的振动,主要与气动力矩和风剪切有关。 风机在运行过程中受到的各种载荷之间是有相互耦合关系的,叶片的拍打与传动系统有耦合关系,塔架的振动与叶片的挥舞有耦合关系,因此在设计风机的过程中,要充分考虑风机的动态载荷,确保机组的运行稳定和使用寿命[3-4]。
针对上述问题,提出基于叶根载荷变换桨距角的控制策略,通过在叶片根部装置压力传感器,对叶根产生的载荷实时监测,以此来反映叶片的受力情况,反映整个机组不平衡载荷的影响,将叶根受到的动态载荷换算为叶轮所弯曲的力矩,将弯曲力矩变换为桨距的反馈量,从而能够对风机进行变桨距控制[5]。
1.2 叶片根部载荷变换桨距角反馈给定计算
风轮在旋转过程中,会受到水平方向和垂直方向的力的作用,因此叶轮的不平衡载荷主要就是水平方向和垂直方向力的弯矩,也就是通常所说的俯仰弯矩Mtilt 和偏航弯矩Myaw,轮毂弯矩受力分析如图1 所示。
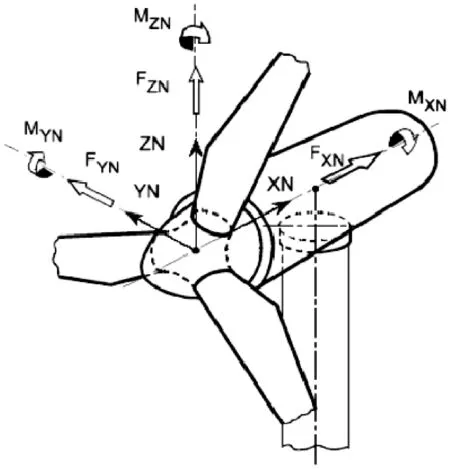
图1 轮毂固定坐标下的载荷
实际运行过程中,轮毂受到弯矩力的作用,引起轮毂的变形和塔架的弯曲,在风场中,经常发生塔筒、叶片折断的情况,发生类似情况的原因是轮毂不平衡载荷引起的,因此通过控制策略来减少论轮毂的俯仰弯矩和偏航弯矩。 但是轮毂的结构是一个球形状的,在实际中,只能利用间接的方法来测量轮毂中心的不平衡载荷,之后再进行换算。 本文是通过叶根载荷变化对轮毂的中心弯矩进行测量的[6-7]。
实际计算中,叶片在叶片坐标系下定义,轮毂在轮毂固定坐标系下定义,为了换算方便,应用了Coleman 坐标变换理论进行坐标变换。
把叶片受到的弯矩根据Coleman 坐标变换理论,变换成轮毂中心俯仰弯矩MYN 和偏航弯矩MZN,其坐标变换公式如式(1)所示。
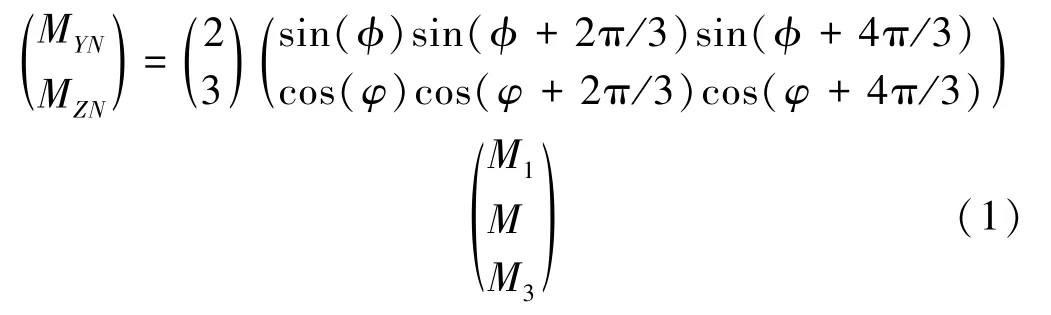
在因为轮毂中心的俯仰弯矩和偏航弯矩互相垂直,没办法只设计一个控制器对其控制,只能设计两个控制器进行控制,把控制器的输出再进行坐标反变换,就可以得到3 个叶片桨距角调节地给定量并对风机进行控制。 其坐标反变换公式如式(2)所示。
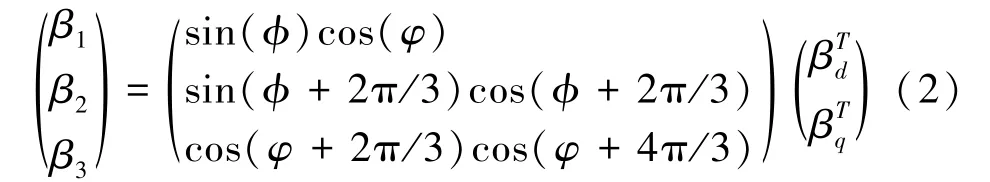
叶片根部气动载荷产生的叶根弯矩线性化模型可表示如下:
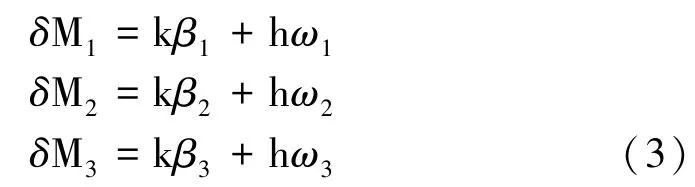
风机叶片转动时的相对风速ω是绝对风速和轮毂前后振动时产生的速度之和,可以由下式(4)所示:

式中:xfa是轮毂振动产生的位移,i为叶片数。
只考虑叶轮前后移动,可以把式(3)和(4)写成:
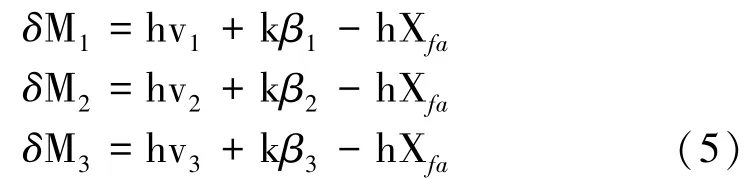
在实际变桨距风机控制时,每个叶片的变桨控制是由统一变桨信号控制的,是根据轮毂中心高度测量的风速大小给人风机控制系统的,系统原理框图如图2所示。
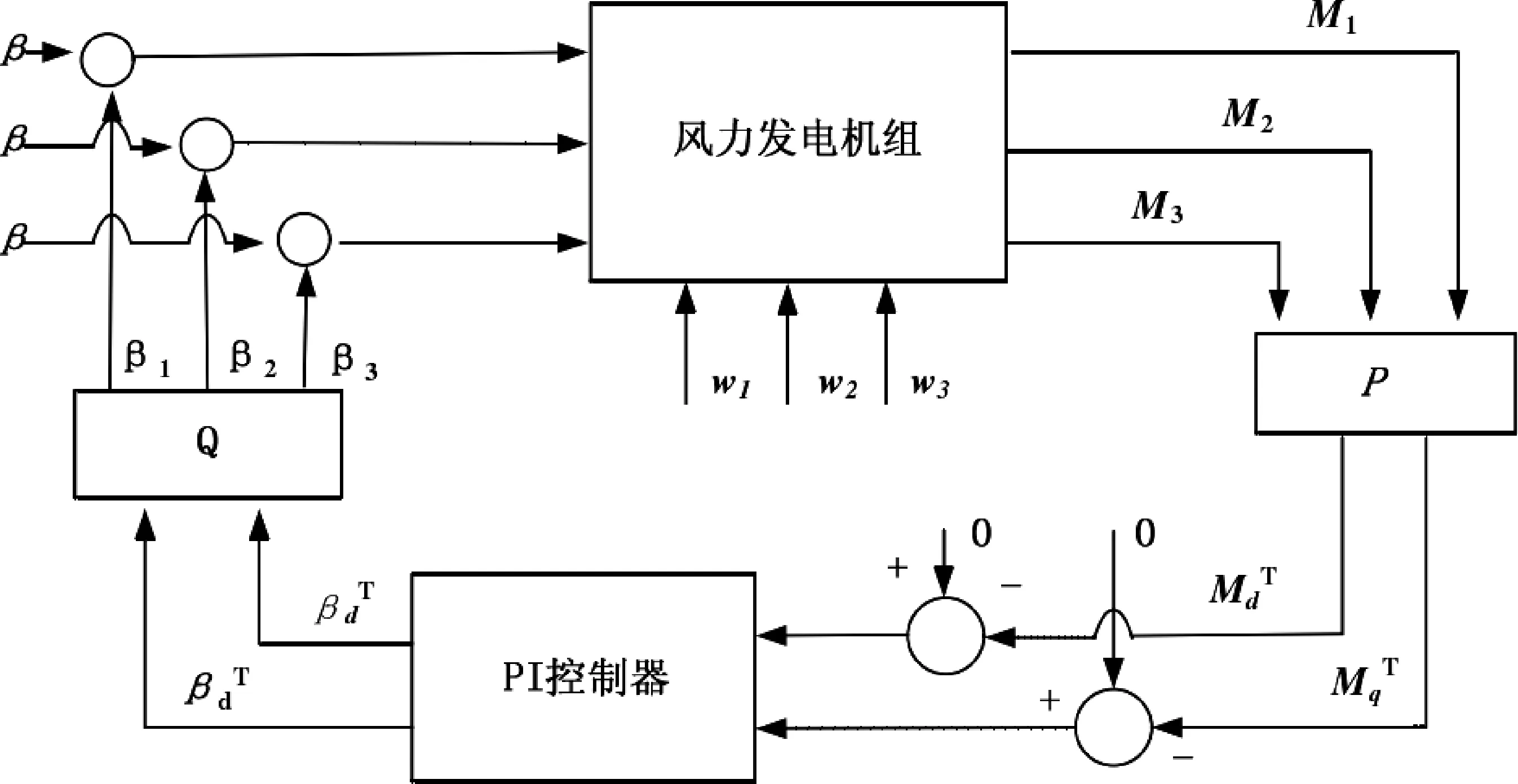
图2 桨距角反馈原理
1.3 叶片根部载荷变换桨距角独立变桨运行分析
(1)在低风速下,叶片受到的各种力的作用较小,产生的载荷也小,一般叶根载荷不作为控制目标来进行控制,但是在兆瓦级风电场中,风机的叶片和塔筒的高度都在几十米以上,叶片的最高点和最低点落差在几十米到一百米之间,在低风速下按照轮毂中心的风速计算最佳叶尖速比是可行的,但是在实际应用中,因为塔筒和叶片长度较大,还应考虑叶片产生的不平衡载荷。
(2)在高风速下,风速超过额定风速,功率超过额定功率时,变桨系统开始工作,由于风度过大,叶片和轮毂受到的气动载荷增加,根据桨叶受力情况,检测出叶根载荷变化情况,计算出俯仰弯矩和偏航弯矩,在通过坐标变换成反馈量,进行控制基于叶根载荷变换桨距角反馈控制。
本文主要研究的就是风速超过额定风速时,如果保持功率稳定及抑制动态载荷对风机的影响,叶片根部载荷变换桨距角反馈控制原理如图3 所示。
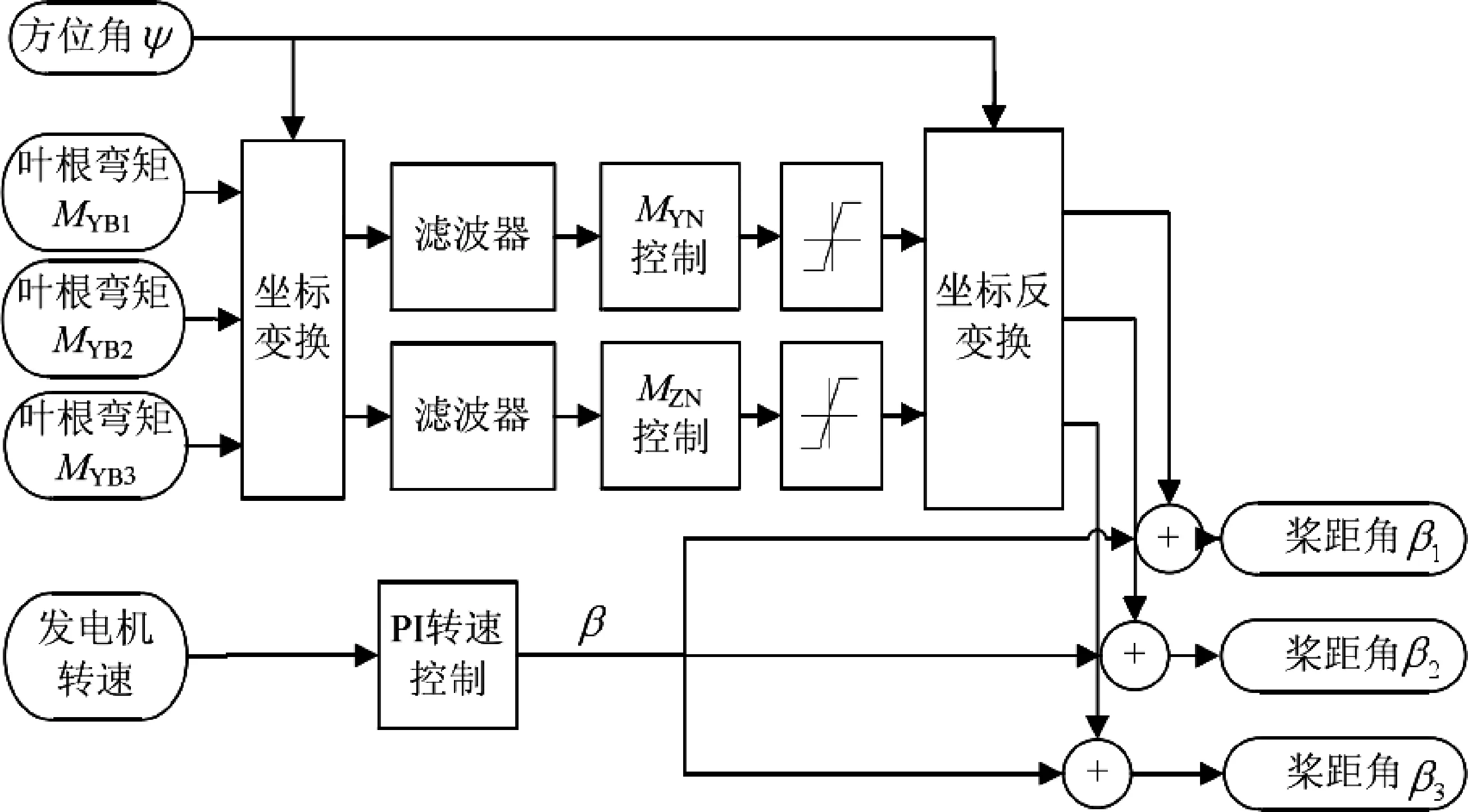
图3 叶片根部载荷变换桨距角反馈控制原理
2 基于桨距角反馈线性化控制器设计
2.1 变桨控制器的设计
为了搭建系统模型,先要通过绝对值编码器检测获取状态变量id、iq、ωr、电磁极位置角θr、转子速度ωr和转子磁极位置角θr。id、iq通过下式坐标变换得到。
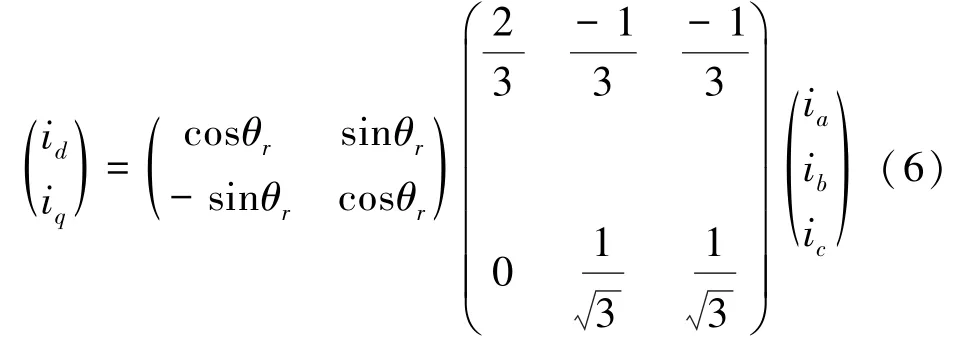
根据三线电机控制系统模型得到:
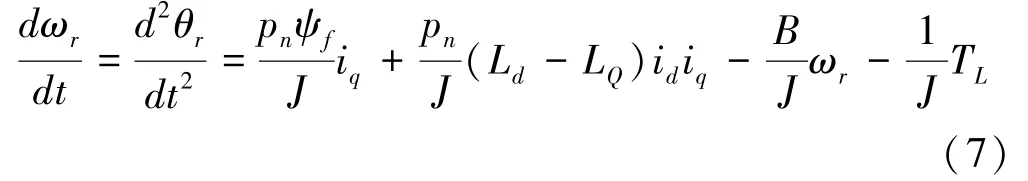
于是电动机的加速度变化率为
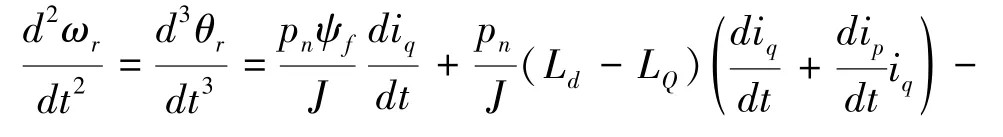
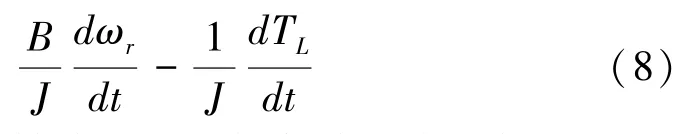
基于桨距角反馈线性化的控制律可表示如下:
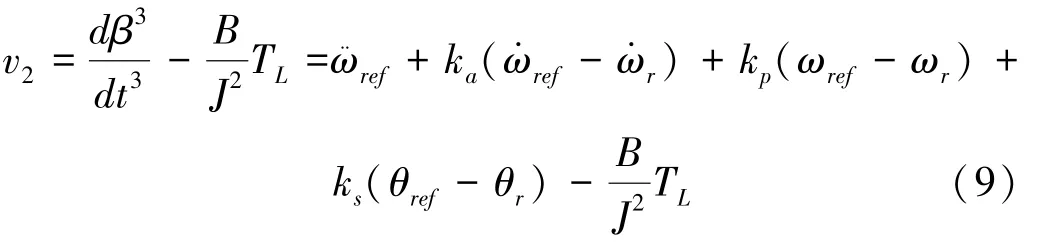
由上式可以看出,该控制系统实际上也是一种以桨距角为输入的伺服驱动电机转速PID 控制系系统,反馈控制律可设计如下:
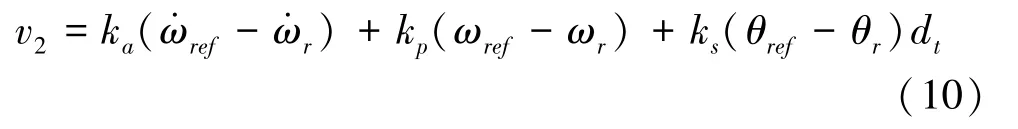
线性化后的闭环系统控制律可设计如下:
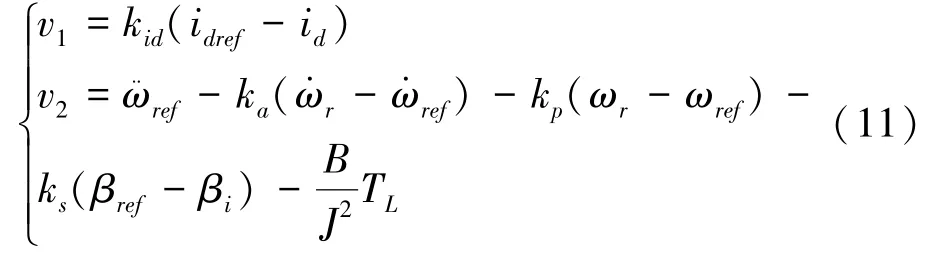
2.2 基于桨距角反馈线性化的独立变桨系统稳定性分析
对于上述桨距角反馈线性化后的独立变桨距控制闭环系统可写成下式:
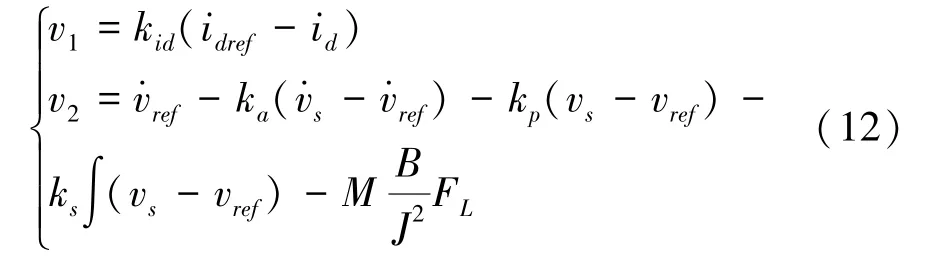
由此系统动态跟踪误差为
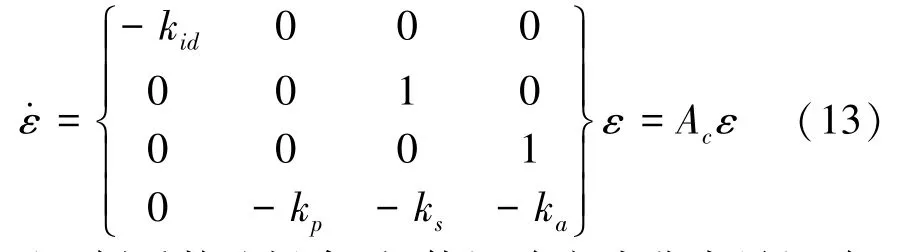
只要比例系数选择合适,使矩阵变成非奇异矩阵,就可以保证变桨系统的快速性和稳定性。
3 系统仿真与结果分析
为了验证设计的基于叶片根部载荷变换桨距角变桨距控制系统的有效性,进行仿真,同时对统一变桨PI控制进行了仿真。 独立变桨结构如图4、图5 和图6 所示。 统一变桨结构如图7 所示。
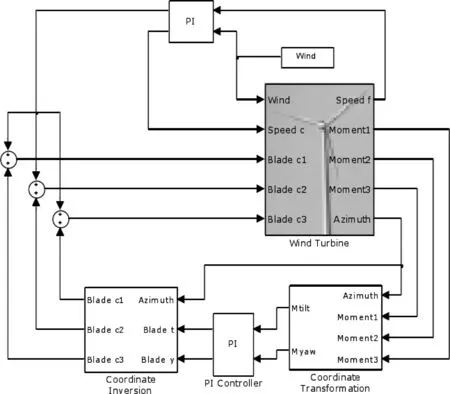
图4 独立变桨系统Simulink 仿真结构
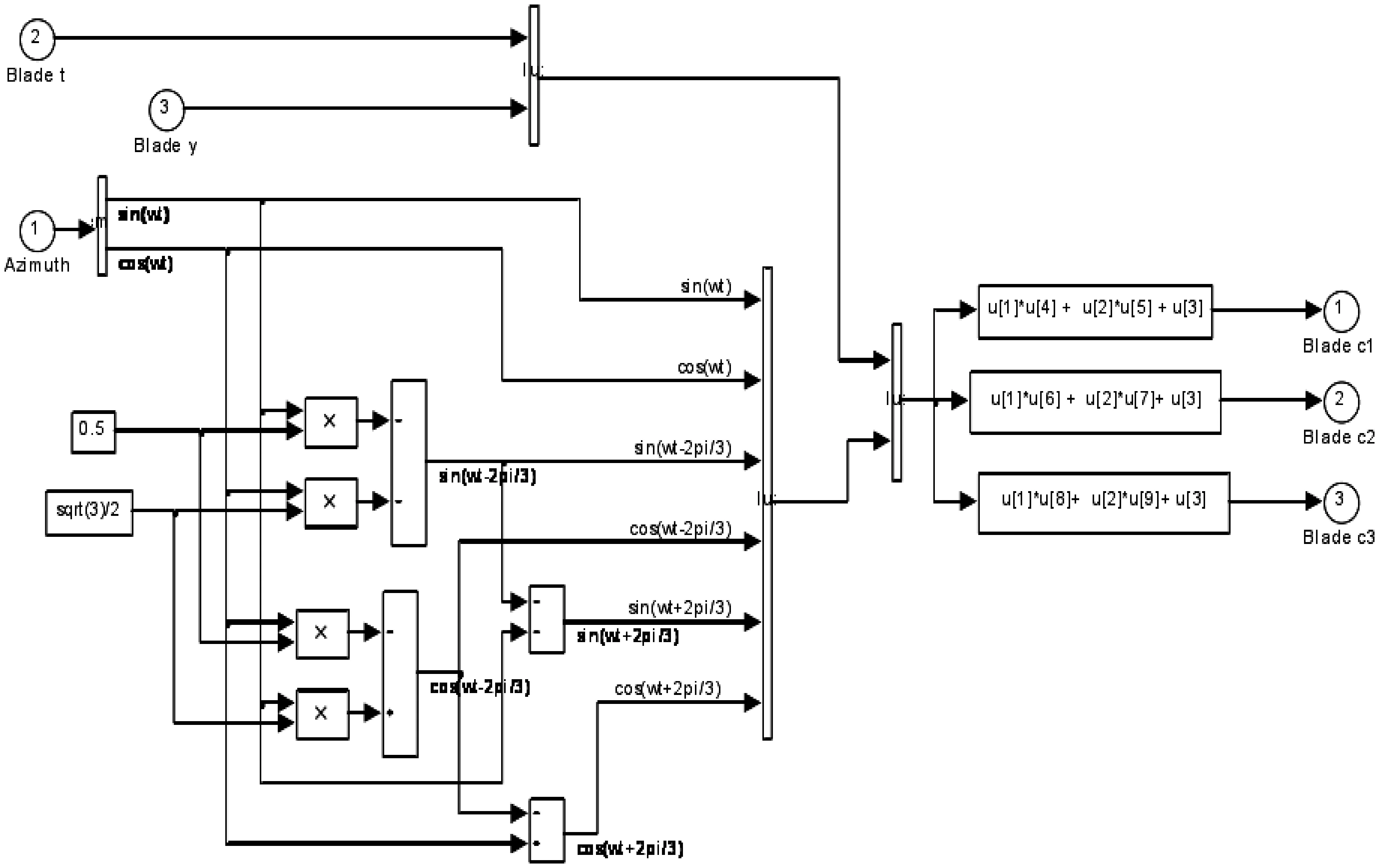
图5 坐标变换仿真模块
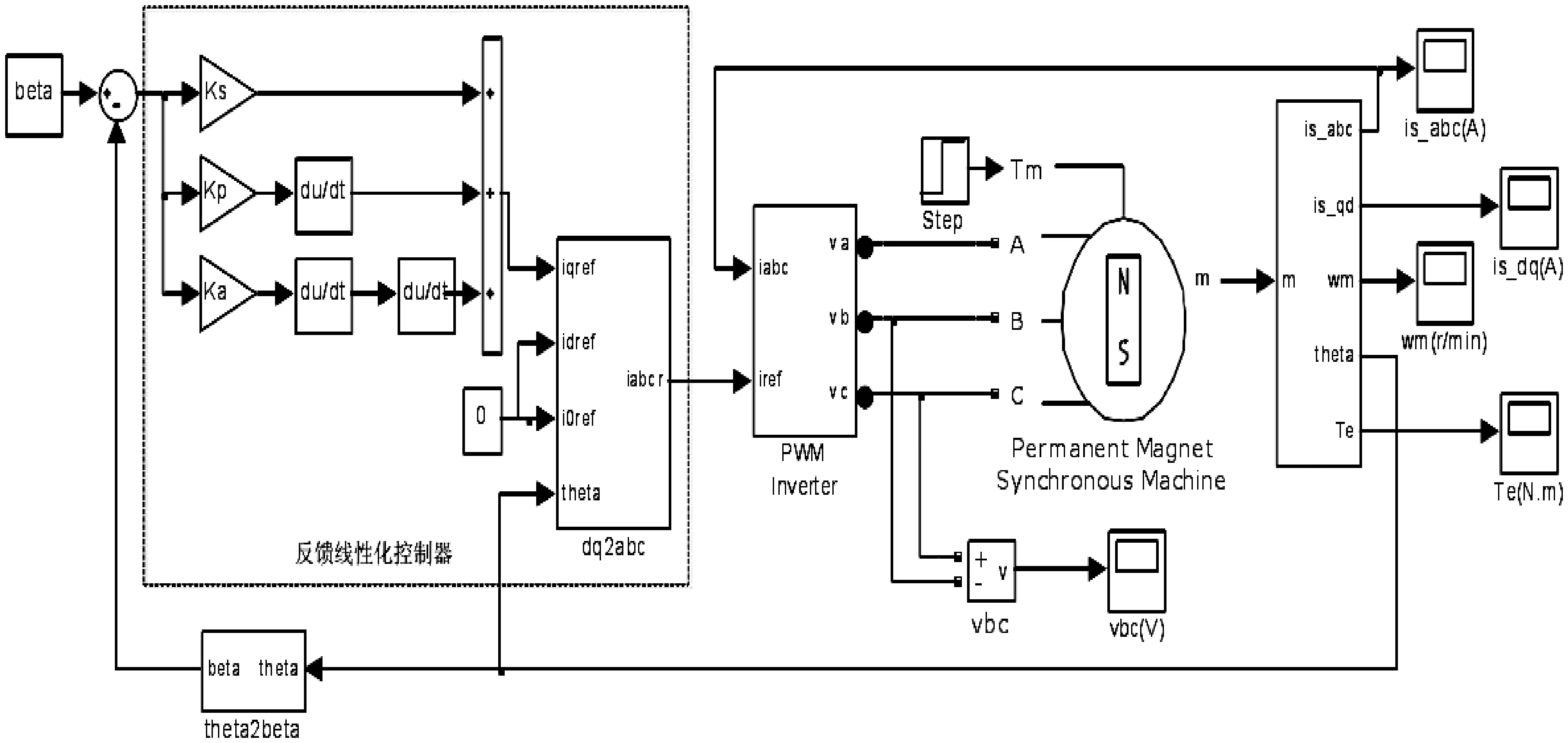
图6 线性化控制 Simulink 仿真模块
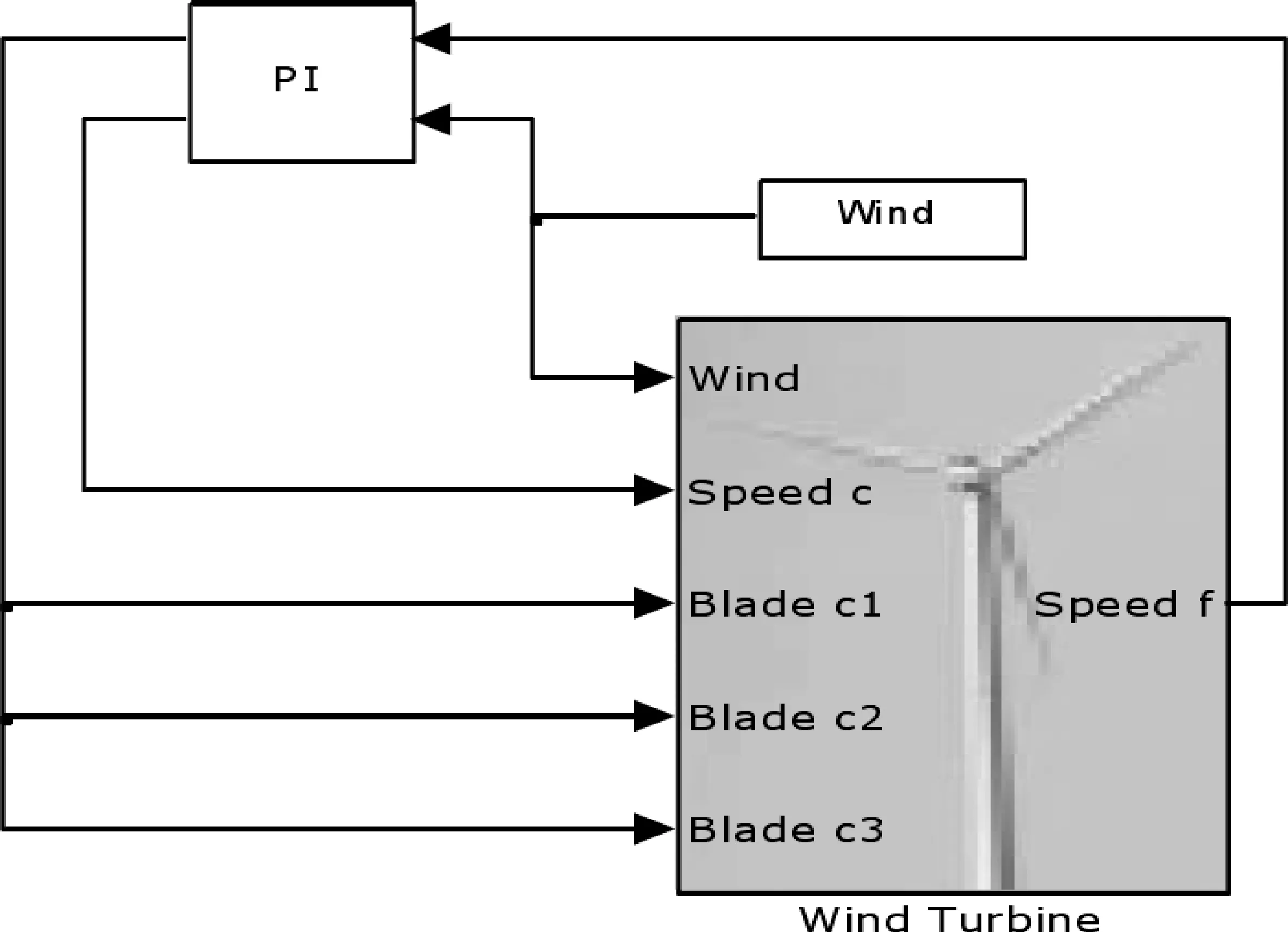
图7 统一变桨距Simulink 仿真结构
独立变桨参数设定如下。 额定功率:P=8 kW;额定转速:N=2 000 r/min;额定电压:U=380 V;额定频率:f=50 Hz;极对数p= 2;电机转动惯量= 0.026 2 kgm2。 控制器参数:kip=20,kp=1.48,ks=0.23,ka=0.015。 统一变桨参数设置为kp=2.63,Ki=0.62。
图8 是充分考虑了风剪切、塔影效应等外在不确定因素的影响下,在轮毂中心高度处以18 m/s 的湍流风速模拟生产的,把它作为模拟仿真时的给定风速。 为了与实际风速相符合便于结果分析,在给定风度时间为20 s~40 s 之间截取一段风速作为仿真风速。
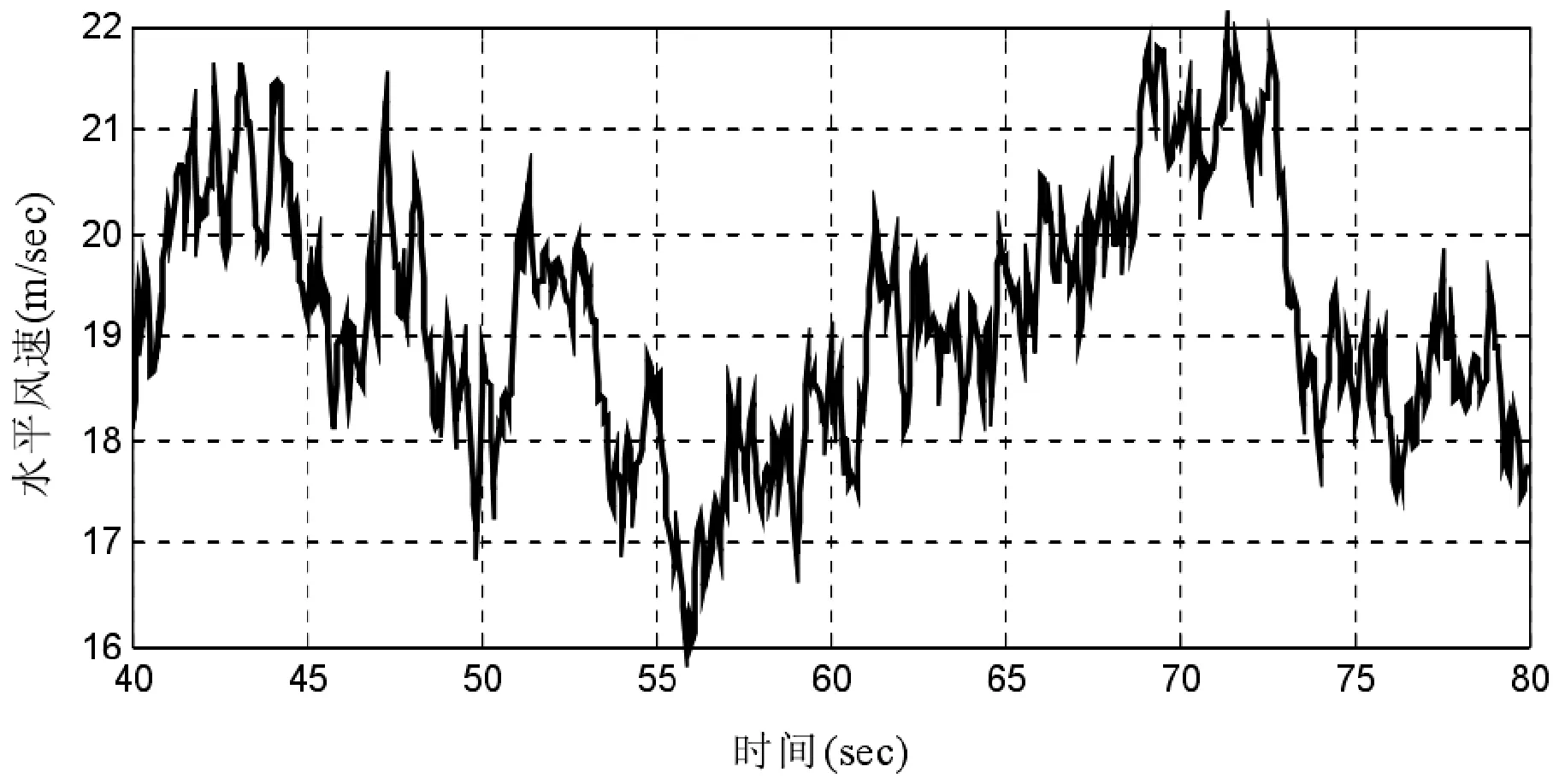
图8 给定仿真风速曲线
系统仿真结果如图9—12 所示,图9 为桨距角随风速变化的调节曲线。
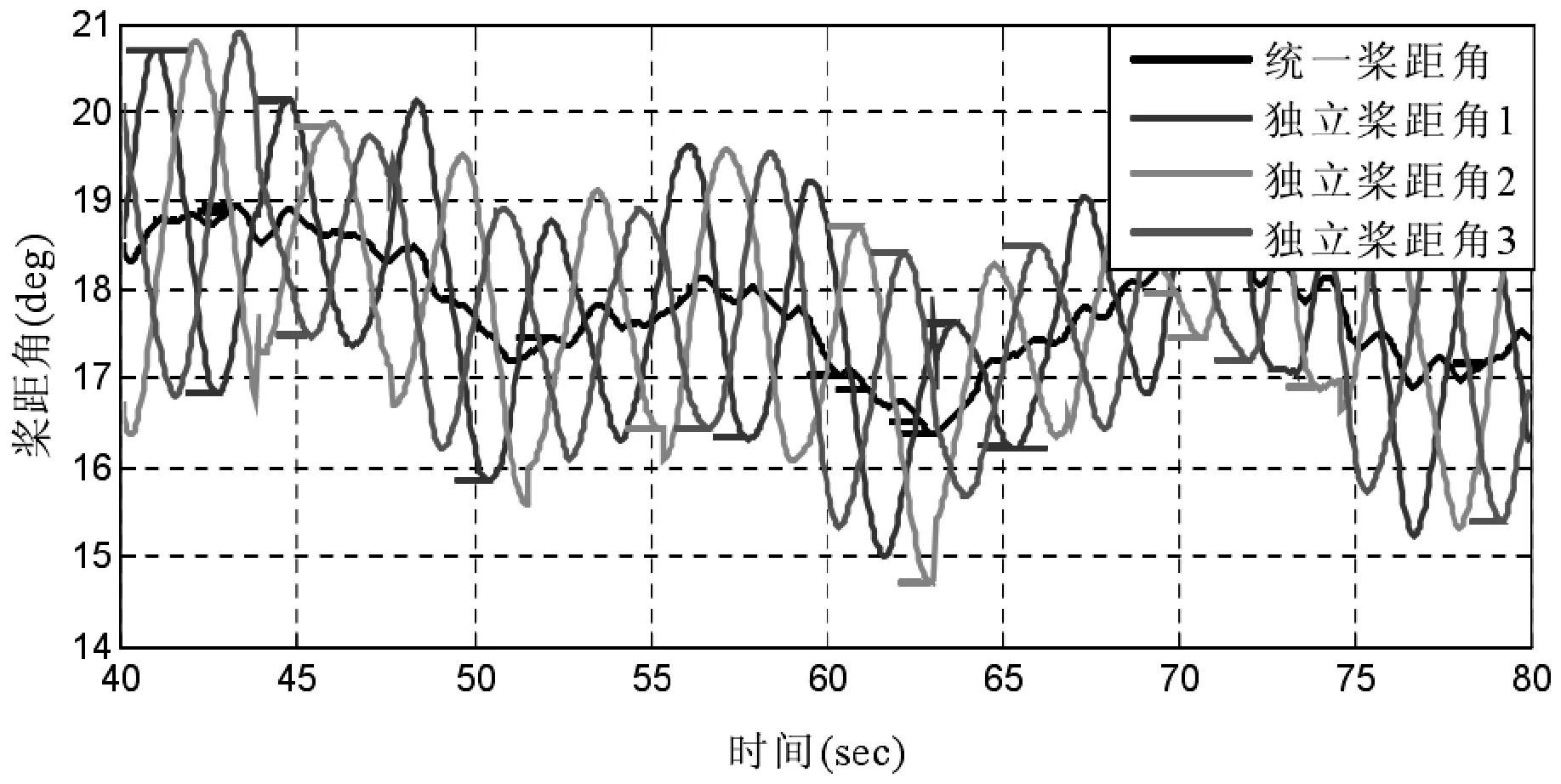
图9 桨距角变化曲线
图10 为两种变桨控制方式下,叶片根部载荷变化图,从图中很明显的就可以看出,在相同风速下,独立变桨距控制的叶根载荷变化幅度小,外在不确定因素对轮毂影响小,系统的稳定性好。
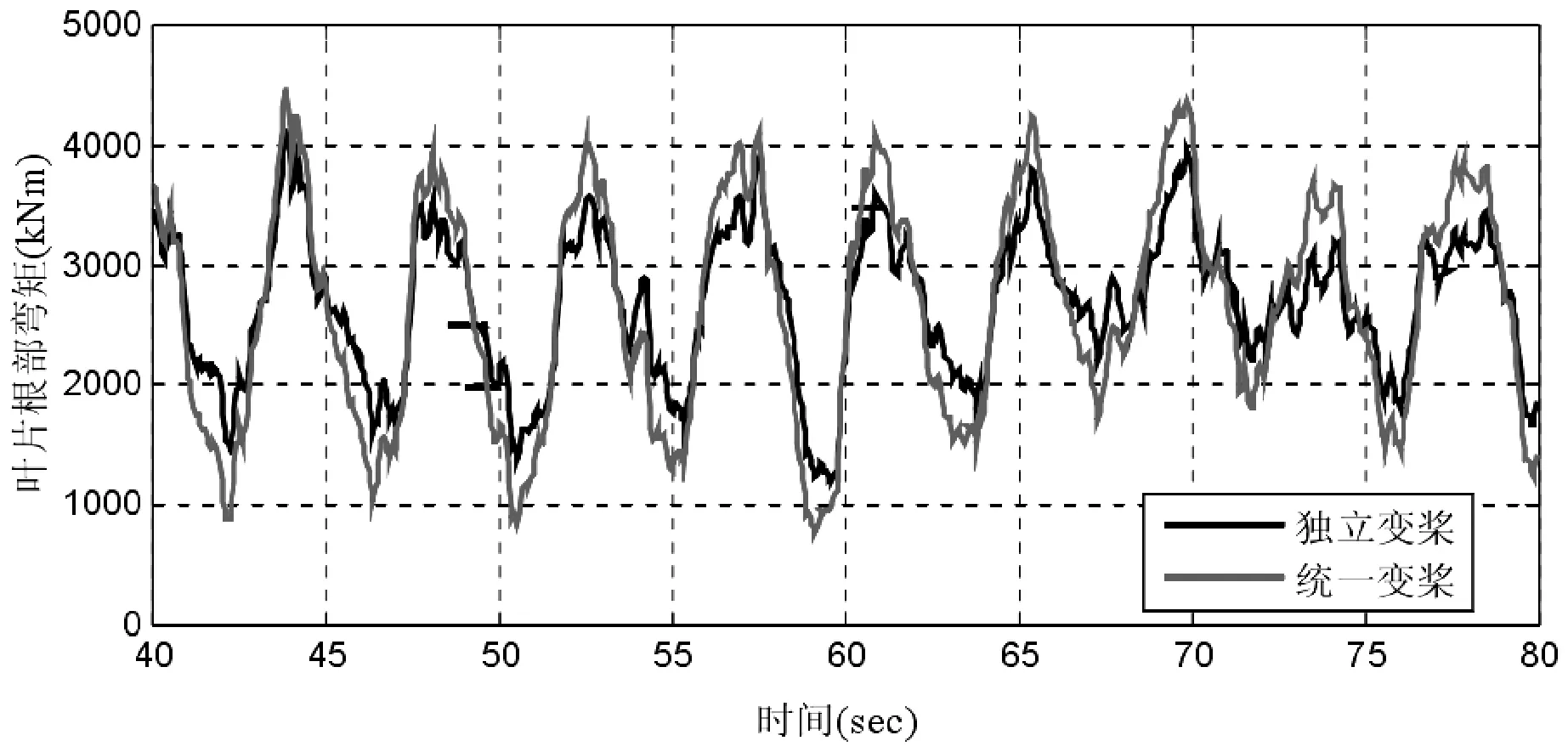
图10 两种控制方式下叶根载荷变化曲线
图11 和12 为两种变桨控制方式下,俯仰弯矩和偏航弯矩曲线对比图,从图中可以看出,两种控制方式在风机运行过程中,俯仰弯矩和偏航弯矩都发生及波动,但是独立变桨距控制的弯矩幅度明显小,说明独立变桨距能够抑制不平衡的载荷。
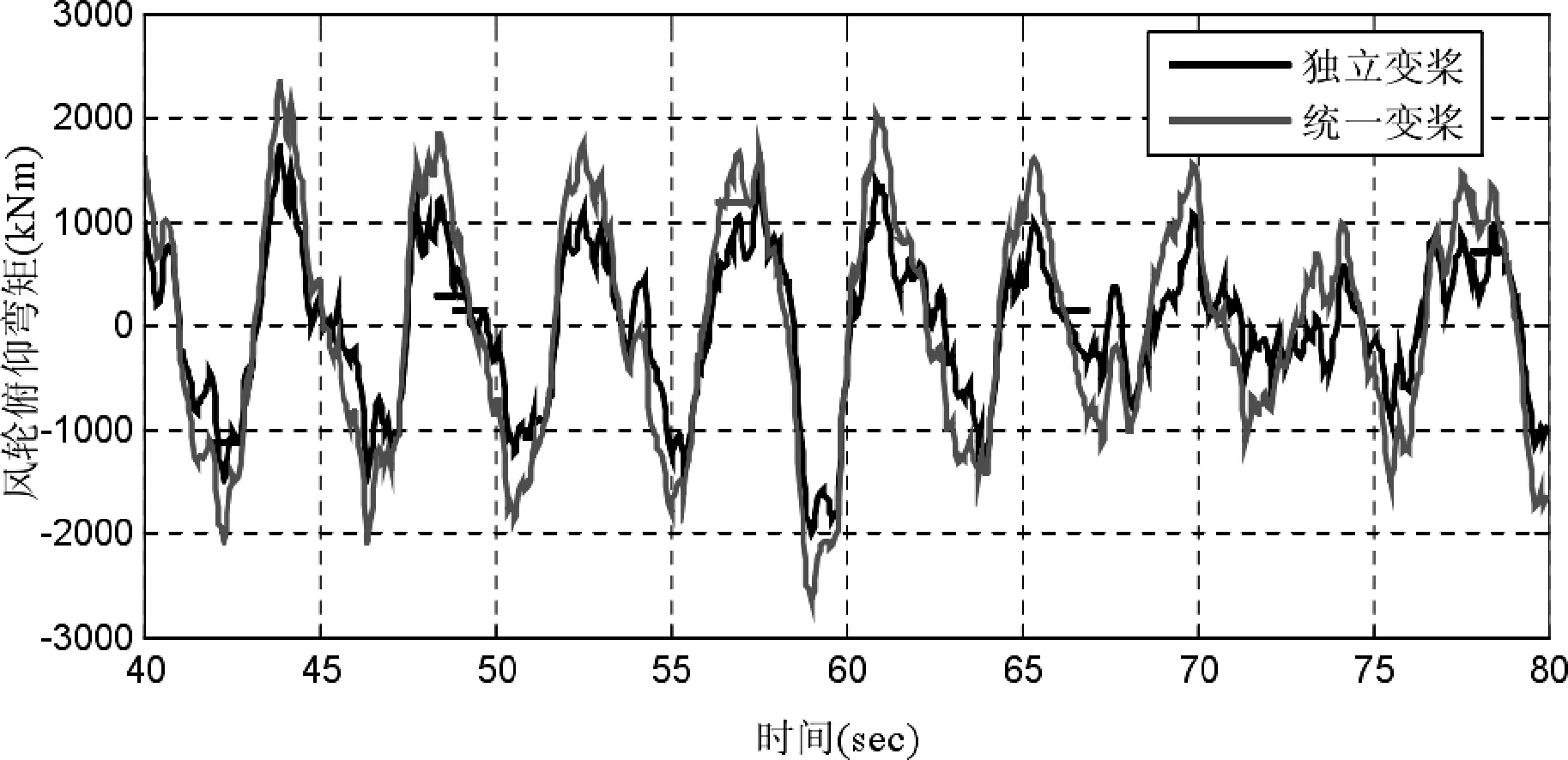
图11 两种变桨下的风轮俯仰弯矩曲线
4 结语
本文对轮毂运行中的载荷进行分析,得出动态载荷对风机的影响较大,提出基于叶片根部载荷变换桨距角反馈线性化的独立变桨距控制策略,通过Coleman变换理论,把叶片根部的载荷量变换成轮毂的动态载荷,在反变换,转换成桨距角的给定量进行控制。 对于独立变桨距控制和统一变桨距控制的仿真分析,结果表明独立变桨距控制比统一变桨距控制的叶根载比变化幅度小,俯仰弯矩和偏航弯矩也小,因此,独立变桨距控制能够抑制不平衡的载荷,系统的稳定性更好。
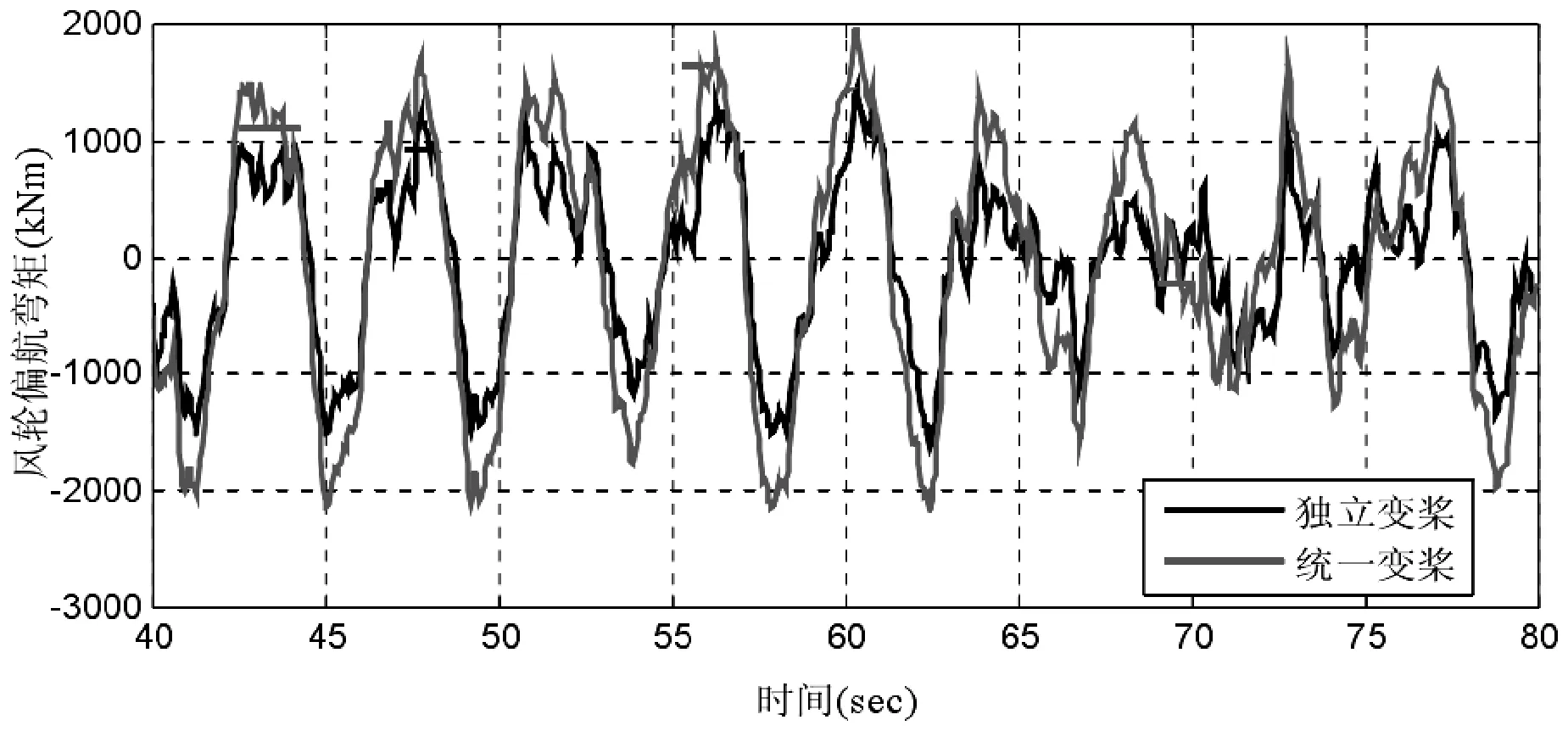
图12 两种变桨下的风轮俯仰弯矩曲线风轮偏航弯矩曲线

