基于多智能体仿真的多方式通勤出行行为研究

李青桐时柏营孔祥科王靖谊

(山东建筑大学 交通工程学院，山东 济南250101)

0 引言

高峰时段的道路拥堵是世界各大城市亟待解决的发展难题。 通勤者作为高峰出行的主体，其固定的路线形成通勤走廊。 通勤走廊是以城市某条主干路为轴线，用于连接职住区并综合多种交通方式以满足通勤者出行需求的客流密集带[1-2]。 早晚高峰时段通勤走廊的交通需求和道路负荷过高，容易引发通勤走廊瓶颈处的交通拥堵。 许多学者针对如何快速消除高峰时段的通勤走廊瓶颈拥堵展开研究，其中对通勤路段和个体出行行为的研究已成为近几年的热点。

在对通勤路段的研究中，VICKREY[3]提出的瓶颈模型成为分析通勤瓶颈路段出行行为选择的重要理论基础，在瓶颈模型中假设职住区之间有一条通行能力有限的道路，由于瓶颈路段通过率有限，因此需要通勤者在出行时间和排队延误惩罚之间权衡，从而使自己的出行成本最低。 在此基础上，KUWAHARA[4]分析了两段瓶颈路段的早高峰通勤问题，并建模分析出行者对出发时间的选择行为。HUANG 等[5]针对公路瓶颈路段研究了小汽车和公交车两种出行方式的出发时间问题。 ZHANG 等[6]从个体工作活动角度出发，研究了个体在道路瓶颈中的拥堵问题。 林震等[7]基于瓶颈模型分析均衡状态下通勤者的出行成本和出行方式。 上述研究集中在理论分析和统计计算，且在模型中设定较多的假设，导致结论往往不具有代表性。

在个体出行行为的研究方面，TORSTEN[8]将出行描述为人类从事期望活动的个体行为，提出了基于活动的出行行为理论。 宗芳等[9]在出行行为理论的基础上，构建了出行方式、出行时间与出行需求间的预测模型。 梁泉等[10]根据调查数据构建公交通勤的个体出发时间和目的地相互关系的结构方程模型。 韩皓等[11]从通勤者决策角度研究小汽车通勤出行行为，探究通勤者出行方式的选择规律。 侯现耀[12]研究了不同延误惩罚下选择公交出行的出发时间选择和公交出行意愿。 胡文君等[13]基于计划延误成本研究通勤者对于出行信息判断与出发时间选择间的影响关系。 上述研究大多只针对一种通勤方式的行为选择，而在现实中，随着可持续交通理念的兴起和共享经济的发展[14-15]，通勤者的通勤方式不再仅仅依靠私家车，而公交、顺风车等通勤方式也逐渐成为了人们的重要选择。

综上可知，目前相关研究存在以下不足:(1) 研究大多集中在数理统计模型的分析和验证，模型中存在大量的主观假设；(2) 对于通勤方式的研究较为单一，缺乏对多种通勤方式并存状态的研究和分析；(3) 通勤者在出行过程中的行为会根据历史经验进行改变，而传统的分析和仿真技术很难对此进行描述。 文章在此基础上，利用多智能体仿真技术对多种方式下的通勤出行进行研究，主要有以下贡献:(1) 考虑多种通勤方式(私家车、公交车、顺风车)下的出行行为选择，分析了通勤方式之间的相互影响；(2) 利用交通仿真软件Sumo 仿真外接Python 中Mesa 智能体框架构建多智能体微观仿真平台。 该仿真平台既可以从微观上更好地刻画出个体通勤行为的选择及其影响因素，而且多智能体存在的学习性[16-17]还可以更真实的仿真通勤者基于历史经验的选择行为。 基于多智能体仿真技术的多方式通勤行为研究不仅为研究出行行为提供了新的技术手段，同时对于优化城市交通管控措施、缓解高峰时段拥堵、发展可持续交通具有重要意义。

1 模型构建

文章以最大化发挥道路资源，最小化通勤个体的通勤成本为期望。 通过构建个体在不同出行方式下的出行成本函数，将最小化通勤成本作为决策依据引入到早高峰出行行为研究中，通过均衡理论推导出各通勤方式在达到均衡状态时的特征。 考虑交通实际和仿真可行性，在文章中只考虑私家车、公交车、顺风车(车主、乘客)4 种通勤方式，并提出以下模型假设:(1) 所有通勤者为同质的，即具有相同的期望到达工作地的时间(即上班时间)和单位时间价值；(2) 出行成本不考虑车辆折旧、停车、违章、事故等额外收费情况；(3) 公交车只行驶在公交专用道，公交车与其他车辆之间的运行相互独立，且认为公交专用道不会在瓶颈处产生排队。

1.1 私家车通勤成本函数

通勤者从家出发驾驶私家车到达工作地，出行成本包括行程时间成本(行驶时间、高峰时段拥堵排队时间)、计划延误成本(早到或迟到延误惩罚)、车辆运行燃油费。 私家车通勤者t时刻乘坐私家车的通勤成本函数由式(1)表示为

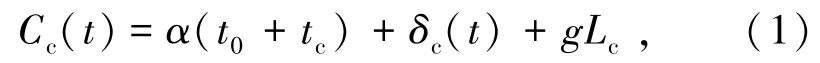
式中Cc(t) 为t时刻私家车通勤成本，元；α为单位时间价值(Value of Time，VOT)；t0为自由流行驶时间，s；tc为小汽车在高峰时瓶颈拥堵的排队时间，s；δc(t) 为私家车计划延误成本，元；g为车辆每公里燃油费，元/km；Lc为私家车通勤的行驶距离，km。

私家车的计划延误成本主要由通勤者实际到达工作地和上班时间的差值，与单位时间惩罚成本系数乘积得到，分为早到延误惩罚和迟到延误惩罚:期望到达工作地时间即开始上班时间为tw，那么计划延误成本由式(2)表示为

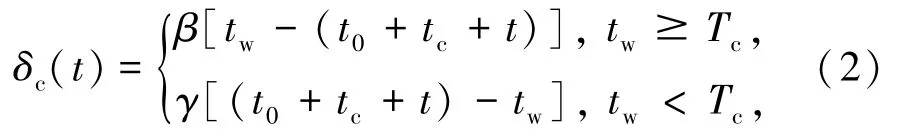
式中β为早到工作地的计划延误惩罚系数，元/h；γ为迟到工作地的计划延误惩罚系数，元/h ；Tc=t0+tc+ t为私家车通勤的总行程时间，s。

1.2 公交车通勤成本函数

通勤者乘坐公交车通勤成本包括:行程时间成本(从家出发到公交车站的时间、等待公交车的时间、乘坐公交车的时间)、计划延误成本、乘坐公交车票价成本。 公交通勤者在t时刻乘坐公交车的通勤成本函数由式(3)表示为

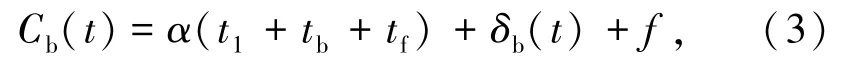
式中Cb(t) 为公交车通勤成本，元；t1为从家出发到公交车站的时间，s；tb为在公交车站的等待时间，s；tf为乘坐公交车的时间，s；δb(t) 为公交车计划延误成本，元；f为公交票价，元。

公交车通勤的计划延误成本由公交车发车次序决定。 假设编号为①的公交车能够保证通勤者准时到达工作地，那么若公交车发车早于或晚于①号公交车将会带来早到延误惩罚和迟到延误惩罚。 计划延误成本由式(4)表示为

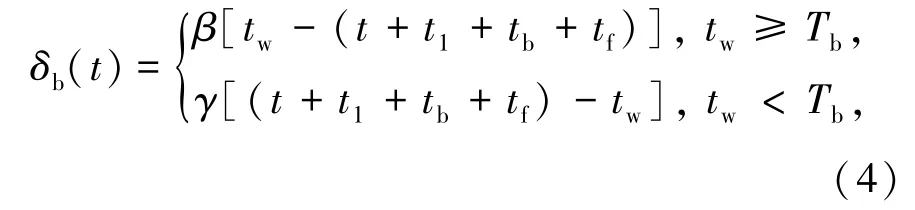
式中Tb=t +t1+tb+tf为乘坐公交车通勤的总行程时间，s。

1.3 顺风车通勤成本函数

顺风车是同路出行的一种绿色出行方式，旨在环保节能，减缓交通压力。 通勤者需要提前发布个人行程信息，顺风车车主根据所接收的行程信息判断是否搭载通勤者。 若两者顺路，则一同前往工作区；若不顺路，则挑选其他符合条件的乘客信息，直到没有顺路的通勤者或没有选择顺风车通勤的乘客为止。 顺风车通勤成本分为顺风车车主和乘客两部分。

(1) 顺风车车主通勤成本有车主行程时间成本(车主接送乘客的时间、车主到达自己工作地的时间、高峰瓶颈处排队时间)、车辆行驶距离成本、计划延误成本，以及从顺风车平台赚取一定比例的费用。 当车主赚取的收入大于自身出行的费用支出时，顺风车车主的通勤成本呈现负数。 顺风车车主的通勤者在t时刻的通勤成本函数和计划延误成本由式(5)和(6)表示为

式中Cs(t) 为顺风车车主的通勤成本，元；t2为顺风车接送乘客所花费的时间，s；ts为车主从乘客下车点到达工作地的时间，s；tc为瓶颈处的排队时间，s；δs(t) 为顺风车车主的计划延误成本，元；Ls为车主接送乘客并到达自己工作地的总行驶距离，km；μ为车主从顺风车平台赚取比例；λ为顺风车平台设置的每公里计费标准，元/km；Lp为车主接送乘客至目的地的行驶距离，ω为顺风车平台设置的每小时计费标准，元/h；tp为乘客上车后的行程时间，s；Ts=t2+ts+tc+tp+t为顺风车车主的通勤的总行程时间，s。

(2) 顺风车乘客的出行成本有乘坐顺风车通勤的行驶时间(上车后的行程时间、高峰瓶颈处排队时间)、乘坐顺风车的支付成本和计划延误成本。顺风车乘客的通勤者在t时刻的通勤成本函数和计划延误成本由式(7)和(8)表示为

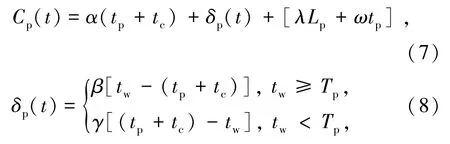
式中Cp(t) 为乘客的通勤成本，元；tp为乘坐顺风车的行驶时间，s；δp(t) 为顺风车乘客的计划延误成本，元；Lp为乘客乘坐顺风车至工作地的距离，km；Tp= tp+ tc为顺风车乘客乘坐顺风车通勤的总行程时间，s。

1.4 均衡分析

Wardrop 平衡原理[18]假设所有出行者都能明确路网中存在拥堵情况，即所有出行者能够根据拥堵情况来估算不同出行方式下的费用，并以费用最小作为决策的依据。 随机用户均衡原理认为在最终均衡的状态下，所有人都具有相同的费用，且出行个体不能通过改变自身出行方式来降低费用。

根据瓶颈模型[3]，随着高峰时通勤需求逐渐增加，小汽车(私家车、顺风车)会在道路瓶颈处产生拥堵。 拥堵排队时间随着通勤需求的增加而增加，且通勤者对出发时间和出行方式的选择也会受到通勤需求增加的影响。 考虑到公交车的实际运营情况，设定公交专用道的通行能力大于公交车到达率，即公交车不会在专用道上产生拥堵。

瓶颈处拥堵仅有小汽车，且小汽车的道路资源已经达到全负荷状态，小汽车排队数量近似等于排队人数为N = N1+ ηN2(η为顺风车通勤的人数比例)，瓶颈处通行能力为S，整个拥堵时段为[tstart，tend]，那么排队人数由式(9)表示为

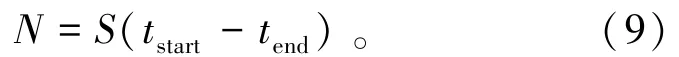
假定tz为通勤者tw准时到达工作地的出发时刻，最早和最晚出发的通勤者可以避免拥堵排队，但需要面临早到延误惩罚和迟到延误惩罚，相应惩罚成本由式(10)表示为

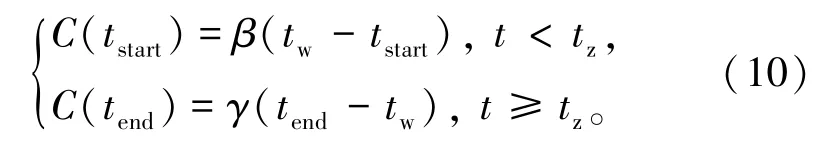
在最终均衡状态下，所有通勤者的出行成本相等，可求出关键时刻点由式(11)～(13)表示为

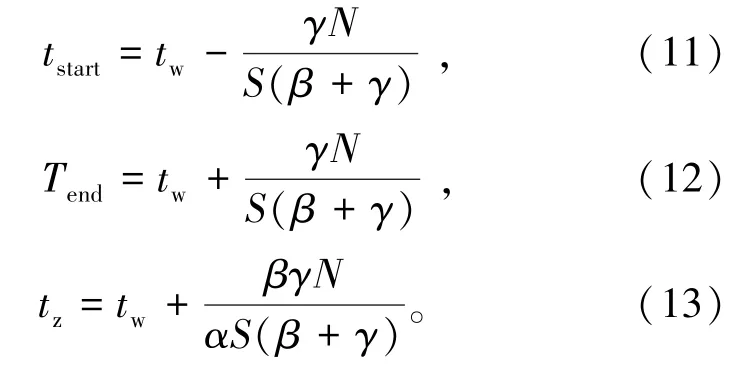
此时，瓶颈处的到达率由式(14)表示为

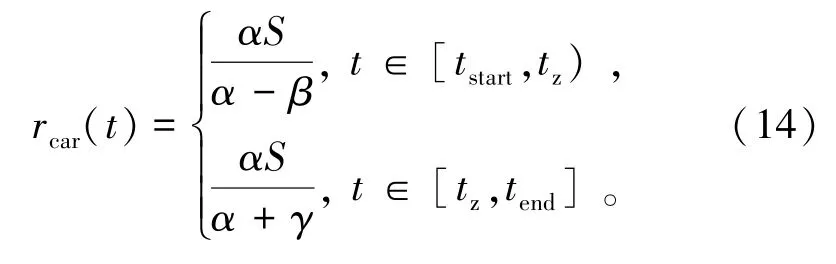
由于早高峰整个拥堵时段，小汽车行驶道路处于全负荷状态，瓶颈处的到达率为瓶颈处的通行能力，即Rcar(t)= S。 根据公式(11)～(14)，可以求得小汽车通勤的成本由式(15)表示为

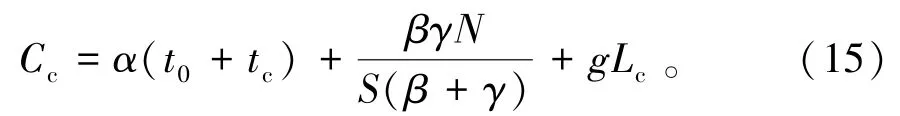
由于仿真设定公交车不产生拥堵，乘坐公交车通勤的个体不包含排队时间，且公交车的发车率fb等于其到达率，故第i辆公交车通勤的成本由式(16)表示为

在后续讨论中将进行多智能体仿真，模拟通勤者以成本最小化作为目标的出行决策，从而保证通勤个体所获效益最大。

2 仿真分析

2.1 仿真环境与平台

仿真采用Python 中Mesa 智能体框架和Sumo城市交通微观仿真软件构建基于多智能体的多方式通勤出行仿真平台。 Mesa 是基于智能体进行建模、分析、可视化的Python 框架；其优势在于可以定义一个Agent 类，实现多智能体之间的交互协作。Sumo(Simulation of Urban Mobility)是德国宇航中心开发的用于城市道路交通的微观仿真软件，是一种开源、微观、多模态的交通模拟过程。 其允许模拟在给定交通需求下单个车辆在路网中的移动，是一种时间离散、空间连续的模拟。 相比于传统的交通仿真系统，文章构建的自学习多智能体仿真平台能够实现智能体之间、智能体与环境之间的相互学习，进行自主学习和自主预测。 在微观仿真平台下，能够更精细的模拟每位通行者的出行行为。 仿真流程如图1 所示。

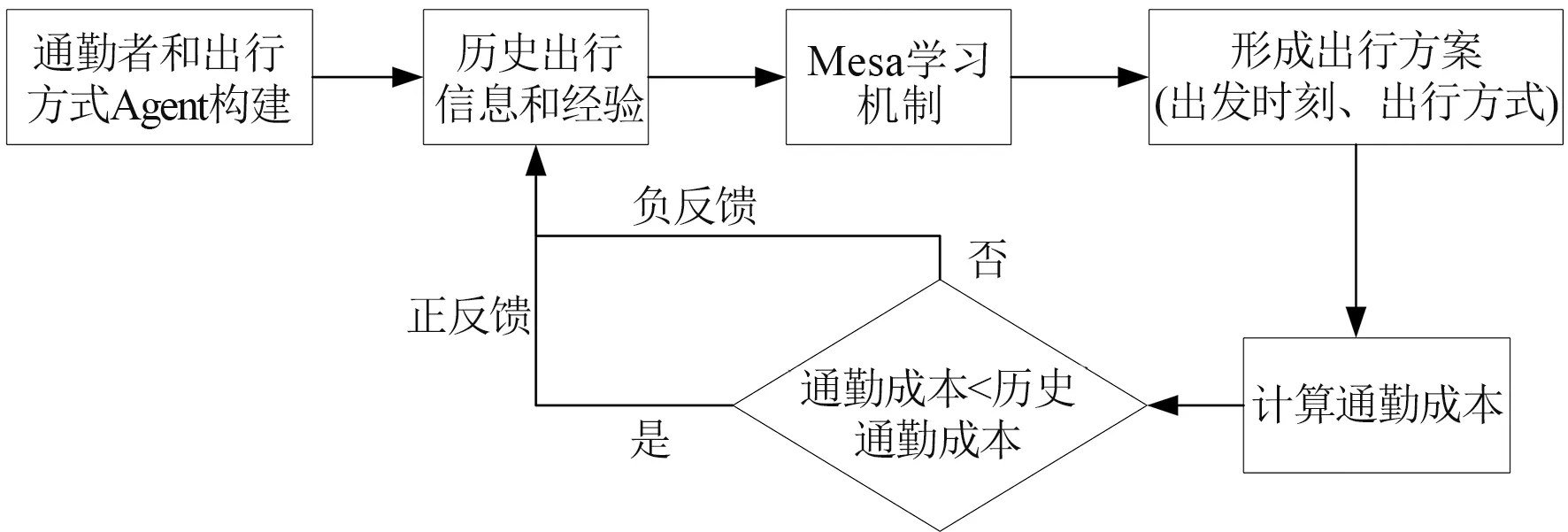
图1 仿真流程图

在微观连续道路交通仿真平台中构建通勤走廊瓶颈，通勤走廊为单向道路，即从居住地出发到达工作地。 道路包含五条车道:1 条公交专用道和4 条机动车道。 在瓶颈处，将机动车道设为2 条。 假设通勤者的居住地位于通勤走廊起点位置，区域面积为1 000 m×1 000 m。 仿真程序一共模拟了通勤者一个月(30 d)的出行情况，将通勤者开始工作的时间设定为9:00，出发时间设定为8:00 ～8:50 之间。 考虑实际出行情况以及文献[19-20]参考，仿真程序中用到的具体参数如下:平均单位时间价值α=10 元/h，早到惩罚系数β= 6 元/h，迟到延误惩罚系数γ=22 元/h，燃油成本g=1.5 元/km，公交票价为2 元，顺风车每公里计费标准λ=1.5 元/km，顺风车每小时计费标准ω=24 元/h，顺风车车主从平台赚取比例μ=90%。

2.2 学习性验证

为了验证仿真平台的自学习性，设定通勤者人数为2 000 名，将初始通勤方式比例设置为私家车∶公交车∶顺风车车主∶顺风车乘客= 0.5 ∶0.3 ∶0.1 ∶0.1[21-22]，分别选取第1、15、30 天的出发时刻、出行时间和个人成本进行比较，可视化结果如图2 ～4 所示。 红色代表私家车通勤，蓝色代表公交车通勤，绿色表示顺风车车主，橙色表示顺风车乘客。 图2 ～4的横坐标表示为仿真中通勤者人数，图2 的纵坐标表示通勤者出发时间(初始时间为8:00)；图3 的纵坐标表示通勤时间；图4 纵坐标表示通勤者选择不同出行方式所花费的成本。

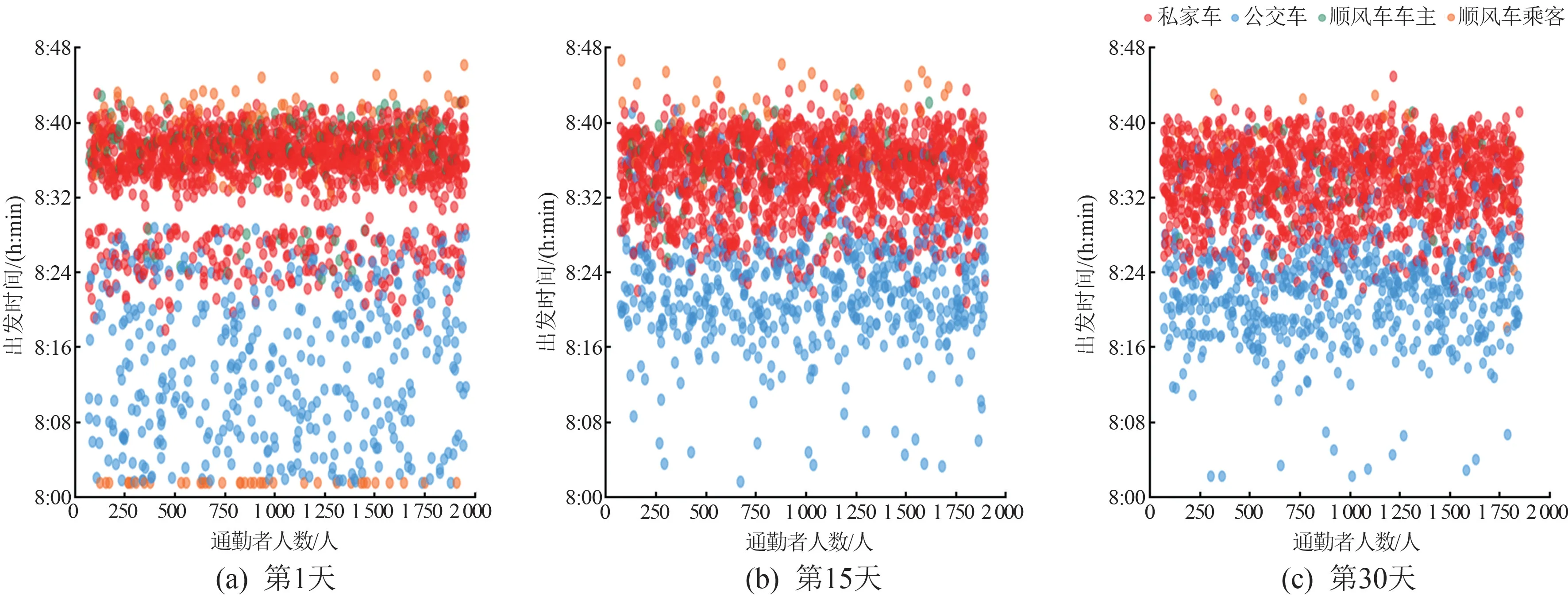
图2 不同仿真天数的通勤者出发时刻图

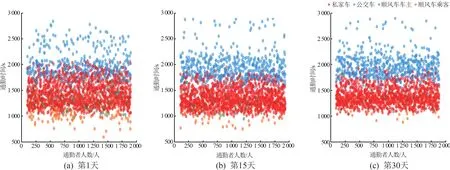
图3 不同仿真天数的通勤时间图

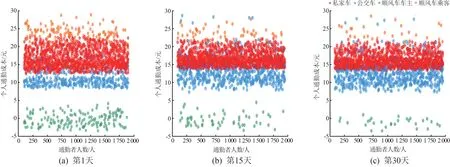
图4 不同仿真天数的个人通勤成本图

由图2～4 可以得出，在仿真实验初期，每种通勤方式的通勤者的出发时间、出行时间分布比较分散，而随着仿真时间的增加，每种通勤方式的通勤者的出发时间、出行时间分布逐渐收敛，且趋于稳定。以公交车通勤为例:在仿真第1 天通勤者的出发时间分布在8:00—8:35，通勤时间分布在25～50 min；而在仿真第15 天和第30 天，通勤者的出发时间主要分布在8:15—8:30，通勤时间主要分布在30 ～40 min。 从图4 各人通勤成本上来看，随着仿真时间的增加，个人的通勤成本分布范围更为集中，个人的平均通勤成本也明显降低。

在不断地关注和肯定信息技术的优势后，人们开始回归教育人文关怀的本质，反思在信息化教学中过多关注人机交互造成的师幼间情感缺失。认为“师幼互动所蕴含的教育智慧及人与人之间的信任、鼓励、关怀等温情永远是教育教学的重要组成部分[6]”，教师自身的人格魅力会对幼儿产生积极影响，可以通过语言和体态语去传递情感，形成互动。师幼互动的教学灵活性也可以弥补教学软件固定程式对教学的制约。

实验表明，随着仿真天数的增加，智能体的决策会趋向于成本低且出行时间短的通勤方式和出发时间。 在现实世界中，随着通勤个体出行次数的增多，通勤者积累的出行经验增多。 此时，通勤者的决策趋向理性，对于出发时间以及出行时间的选择不再盲目判断，而是依据以往经验选择更为合适的出行方案，个人的通勤成本也随之减少。 仿真试验后期也可以看出，通勤个体对自己出行方式的选择更具合理性，个人成本也得到进一步降低，这也验证了多智能体仿真平台的自学习性。

3 计划延误惩罚影响分析

通勤者均设定期望到达工作地的时间，若到达工作地时间早于期望时间时会则会产生早到延误惩罚，若到达工作地时间晚于期望时间则会产生迟到延误惩罚，随着时间差的改变通勤者遭受的延误惩罚程度也不同。 当通勤者遭受早到或迟到延误惩罚时，其物质或心理上产生一定程度的损失，影响通勤者下一次的出行行为选择，因此通过改变延误惩罚系数分析通勤者对惩罚系数的敏感度，以及相应的通勤行为改变。

3.1 早到延误惩罚分析

当通勤者到达工作地时刻早于期望时间时，工作活动未开始，通勤者则需承担早到延误惩罚。 根据文献[21]中单位早到、迟到延误惩罚系数满足γ＞α＞β，因此在仿真实验中，设置不同的早到延误惩罚系数6、7、8、9 来研究通勤者对于早到延误惩罚系数的敏感度和通勤行为改变。

3.1.1 敏感度分析

通勤者对于出发时刻的选择是其综合考虑通勤环境(时间要求、交通状况等)后最直接的行为表现。因此，通过通勤者在不同早到延误惩罚系数下出发时刻的改变来分析通勤者对早到延误惩罚系数的敏感度，如图5 所示。

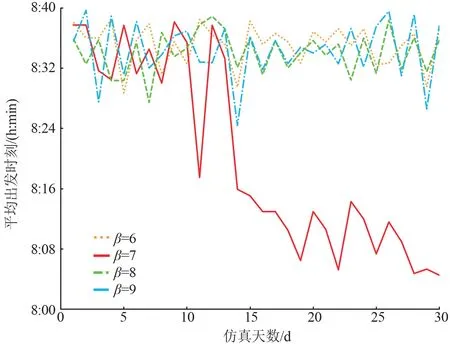
图5 不同早到延误惩罚系数下出发时刻图

在仿真前期，不同早到惩罚对通勤者出发时刻的影响较小，通勤者的平均出发时刻集中在8:30—8:40 时段内。 此时，虽然改变了早到惩罚系数，但是通勤者缺乏历史经验，其出发时刻缺乏合理性；随着通勤者通勤经验的积累，其通勤行为选择更为合理。 在仿真中后期可以明显的看出，当早到延误惩罚系数为7 时，通勤者出发时刻在仿真10 ～15 d 出现明显波动，最终平均出发时刻较为稳定的分布在8:05—8:15 时段内。 因此，当早到延误惩罚系数为7 时，通勤者的敏感度最高。

3.1.2 通勤行为影响

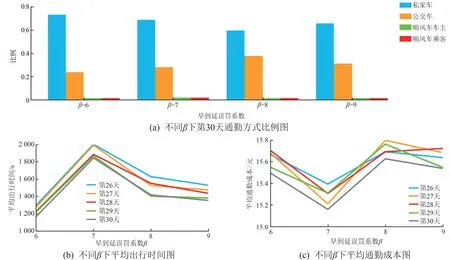
图6 早到延误惩罚下通勤出行图

由图5 和6(a)可以看出，当早到延误惩罚系数低于最高敏感度时，随着β的增加，通勤者的平均出发时刻提前，而通勤方式中公交车占比明显提升；当早到延误惩罚系数高于最高敏感度时，随着β的增加，通勤者的出发时刻明显延后，通勤方式占比也由公交车向私家车和顺风车转移。

这意味着通勤者针对早到延误惩罚增加而采取的主要措施可分为:第一阶段，当β＜7 时，通勤者更多的选择采用公交车通勤的方式并且适当提前出发时刻；第二阶段，当β＞7 后，通勤者对于早到延误惩罚增加的主要反应是延后出发时刻，同时为了避免迟到，通勤者在该阶段更倾向于通过私家车或顺风车通勤。 对应的由图6(b)～(c)可以得出，在第一阶段由于公交车通勤比例的增加，通勤者的平均通勤时间增加，平均通勤成本有所降低；在第二阶段通勤者的平均通勤时间有下降趋势，但是平均通勤成本也有所增加。

3.2 迟到延误惩罚分析

当通勤者到达工作地时刻晚于期望时间时，工作活动已经开始，通勤者会失去部分由工作活动所产生的效益，而承担迟到延误惩罚。 现有研究中关于γ的取值大多采用19 或31[19]，因此在仿真实验中， 将 迟 到 惩 罚 系 数 设 置 为 19、 22、25、28、31来研究通勤者对于迟到延误惩罚系数的敏感度和通勤行为改变。

3.2.1 敏感度分析

根据图7 在不同迟到延误惩罚系数下通勤者出发时刻的改变可以看出，迟到延误惩罚为22 时的通勤者平均出发时刻在仿真第10 ～15 天时，出现明显波动趋势。 在仿真后期，迟到延误惩罚为22 的平均出发时刻稳定在8:05—8:13 时段内，明显低于其他系数取值下的平均出发时刻。 因此，当迟到延误惩罚系数为22 时，通勤者的敏感度最高。

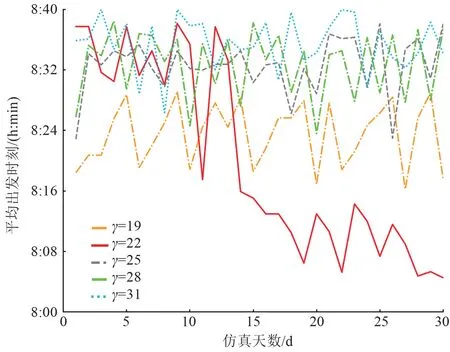
图7 不同迟到延误惩罚系数下的出发时刻图

3.2.2 通勤行为影响

不同迟到延误惩罚系数下仿真末期的通勤方式比例条形图、平均出行时间以及平均通勤成本的变化图如图8 所示。

图8 迟到延误惩罚下通勤出行图

由图7 和8(a)可以看出，当迟到延误惩罚系数低于最高敏感度时，随着γ的增加，通勤者的出发时刻明显提前，但是通勤方式改变较小。 当迟到延误惩罚系数高于最高敏感度时，随着γ的增加，通勤者的出发时刻有一定延后，但此时通勤方式比例出现较大变化，私家车和顺风车的比例提高，而公交车的比例降低。

同样，通勤者针对迟到延误惩罚增加而采取的主要措施也可分为两个阶段:当γ＜22 时，通勤者对于迟到延误惩罚增加的主要反应是提早出发时刻；由图8(b)和(c)可以得出，在这个过程中通勤者的平均通勤时间和平均通勤成本均减少；当γ＞22 时，通勤者对于迟到延误惩罚增加的主要反应包括提早出发时刻和选择私家车通勤；在这个过程中，通勤者的平均通勤时间和平均通勤成本均有所提高。

4 结论

针对城市高峰时段通勤拥堵难题，文章构建了学习型多智能体微观交通仿真平台，通过设置每个智能体根据历史得分调整状态模拟通勤者基于历史情况的通勤选择行为；并且在仿真环境中考虑了多种通勤方式，分别构建通勤成本函数，以符合交通实际情况。 通过仿真分析，主要得出以下结论:

(1) 文章构建的仿真平台对于历史数据具备学习性。 智能体的决策会随着仿真天数的增加，逐渐改变出发时刻和通勤方式以减少个人通勤成本，并在仿真后期趋于稳定。 这意味着该平台能够模拟通勤者基于通勤经验的理性选择，仿真结果更具参考价值。

(2) 通勤行为的选择受多种因素的影响，并体现为通勤者通勤方式、出发时刻、通勤时间的动态平衡，通过基于个体的微观仿真能够直观的描述三者之间的相互关联性，以及不同通勤行为选择的可能诱因。

(3) 通勤者对于延误惩罚具有一定的敏感度。早到和晚到延误惩罚系数分别为7 和22 时通勤者的敏感度最高；当惩罚系数低于或高于最高敏感度时，通勤者往往通过动态调整通勤方式、出发时刻的方式降低通勤成本。