附有限制条件的切比雪夫多项式在精密星历插值中的应用

尹传恒

(中国铁路设计集团有限公司, 天津 300251)

0 引言

为了提升全球导航卫星系统(global navigation satellite system,GNSS)单点定位技术的定位精度,1997年,Zumberge等人提出了利用事先确定的精密卫星星历数据、卫星钟差数据、观测数据解算测站绝对三维坐标的精密单点定位技术(precise point positioning,PPP)[1-4]。在精密单点定位技术中,可获取的GNSS精密卫星星历采样间隔一般为15、5 min,而GNSS观测数据采样间隔为30、15、1 s,两者采样间隔并不一致,因此在精密单点定位数据处理中需要对精密卫星星历进行插值计算,以获取观测数据每一历元所对应的卫星位置。

常见的插值方法有切比雪夫多项式插值、牛顿插值、三次样条插值、拉格朗日插值、广义延拓逼近法插值等,国内众多学者对上述精密卫星星历插值算法进行了详细研究[5-13]。李振昌等人利用滑动式切比雪夫多项式拟合法,分析中圆地球轨道(medium Earth orbit,MEO)、地球同步轨道卫星(inclined geosynchronous satellite orbit,IGSO)、地球静止轨道卫星(geostationary Earth orbit,GEO)的北斗卫星拟合节点数和拟合阶数,达到了亚毫米级的内插精度[5]。廖怡萍等人提出了采用不同阶数的傅里叶级数进行卫星精密星历插值,通过与9阶切比雪夫多项式拟合内插结果比较,证明了采用4阶的傅里叶级数进行MEO精密星历内插精度更高[6]。也有些学者针对精密星历插值中存在的龙格现象进行了相关研究[14-15]。吉长东等人通过对高次多项式拟合与插值数学机理的研究,在精密卫星星历前后各增加15 min已知数据进行拟合和插值计算,有效地避免了龙格现象的发生[14]。虽然这些方法基本实现了卫星精密星历的插值,但仍各有缺点。

在不增加两侧精密星历的条件下,为了保证精密星历的插值精度,且避免龙格现象的发生,本文将利用地面观测数据与卫星精密星历之间的关系,构造限制条件,并结合切比雪夫多项式对精密星历进行插值计算。

1 附有限制条件的切比雪夫多项式

1.1 切比雪夫多项式

设t0为初始历元时刻,Δt为插值区间时长,则在精密星历插值中,首先将t∈[t0,t0+Δt]变换成τ∈[-1,1],以达到时间变量归一化的目的。

(1)

那么,卫星三维坐标分量的切比雪夫多项式可表示为：

(2)

式中,L为卫星三维坐标分量;n为切比雪夫多项式阶数;Ci是X、Y、Z坐标分量的切比雪夫多项式系数;切比雪夫多项式Ti(τ)递推为：

(3)

1.2 限制条件

若地面观测站S的空间坐标为(XS,YS,ZS),则历元时刻t地面观测站S至观测卫星的空间距离ρt为：

(4)

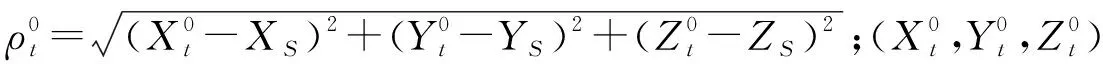
地面观测站S在历元时刻t的载波相位观测值为φt,则此刻地面观测站S至观测卫星的空间距离ρt也可表示为：

(5)

式中,λ为载波的波长;N为载波整周模糊度。

现在，图纸都采用CAD制图，路线的平面图一目了然，有的护栏直接在平面图上标注，除互通匝道的接点不能准确标识外，直线和曲线段基本都和实际施工一样，所以，电脑水平好的话可以直接在电脑上进行设计放线，这样把平面图交给现场人员施工，就不会有长短不一的异形板了，同时也为材料精确的订购提供准确数量。另一种就是现场进行放样，不要要求一次性放到位，根据放样的结果，再重新调整个别立柱间距，《公路工程质量检验评定标准》（JTGF80/1-2004）要求立柱间距±50mm，通过立柱间距或多少使异形板消除或达到0.5m的整数倍。这样经过多次调整，既可以省材料，又可以使后续材料省工、省时。

(6)

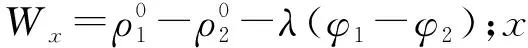
式中,Ti为历元时刻的切比雪夫多项式。

1.3 函数模型

根据切比雪夫多项式原理可得卫星三维坐标分量的函数模型为：

(7)

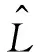
相应的误差模型为：

(8)

由式(1)～式(6)与式(1)～式(8)组成附有限制条件的间接平差模型,即：

(9)

根据附有限制条件的间接平差原理,求得：

(10)

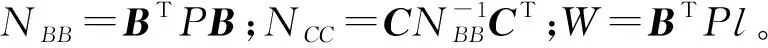
1.4 精度指标

对于附有限制条件的切比雪夫多项式插值结果,本文使用RMS精度指标进行精密星历插值结果,以X方向坐标序列{X0,X1,X2,X3,…,Xn}为例,其各个历元时刻的残差为{ΔX0,ΔX1,ΔX2,ΔX3,…,ΔXn},则：

(11)

2 算例分析

多模GNSS实验跟踪网(the multi-GNSS experiment,MGEX)提供的2016年1月1日的混合精密星历,包含多个卫星定位系统采样间隔为5 min的精密星历数据;IGS站提供的2016年1月1日JFNG站的O文件观测数据,包含多个卫星定位系统的观测数据,采样间隔为30 s。本文以北斗系统(Beidou navigation satellite syetem,BDS)中的GEO类型卫星C01和MEO类型卫星C14、全球定位系统(global positioning system,GPS)中的G06、全球卫星导航系统(global navigation satellite system,GLONASS)中的R01的精密星历为样本进行相关实验分析。

以15 min采样间隔的卫星精密星历为已知节点,首先利用切比雪夫多项式对其进行拟合和插值,分析不同阶次切比雪夫多项式的插值精度,确定切比雪夫多项式的最佳阶次。然后,利用切比雪夫多项式和附有限制条件的切比雪夫多项式对采样间隔15 min的卫星精密星历进行插值,分析比较两种算法的插值精度及稳定性。

2.1 切比雪夫多项式最佳阶次确定

针对BDS系统的GEO卫星和MEO卫星、GPS卫星、GLONASS卫星的采样间隔为15 min的精密星历数据,采用切比雪夫多项式分别进行6～15阶的插值计算。将切比雪夫多项式插值结果两端各1 h数据去掉,削弱龙格现象对四种类型卫星精密星历插值精度统计的影响,详细结果如表1所示。

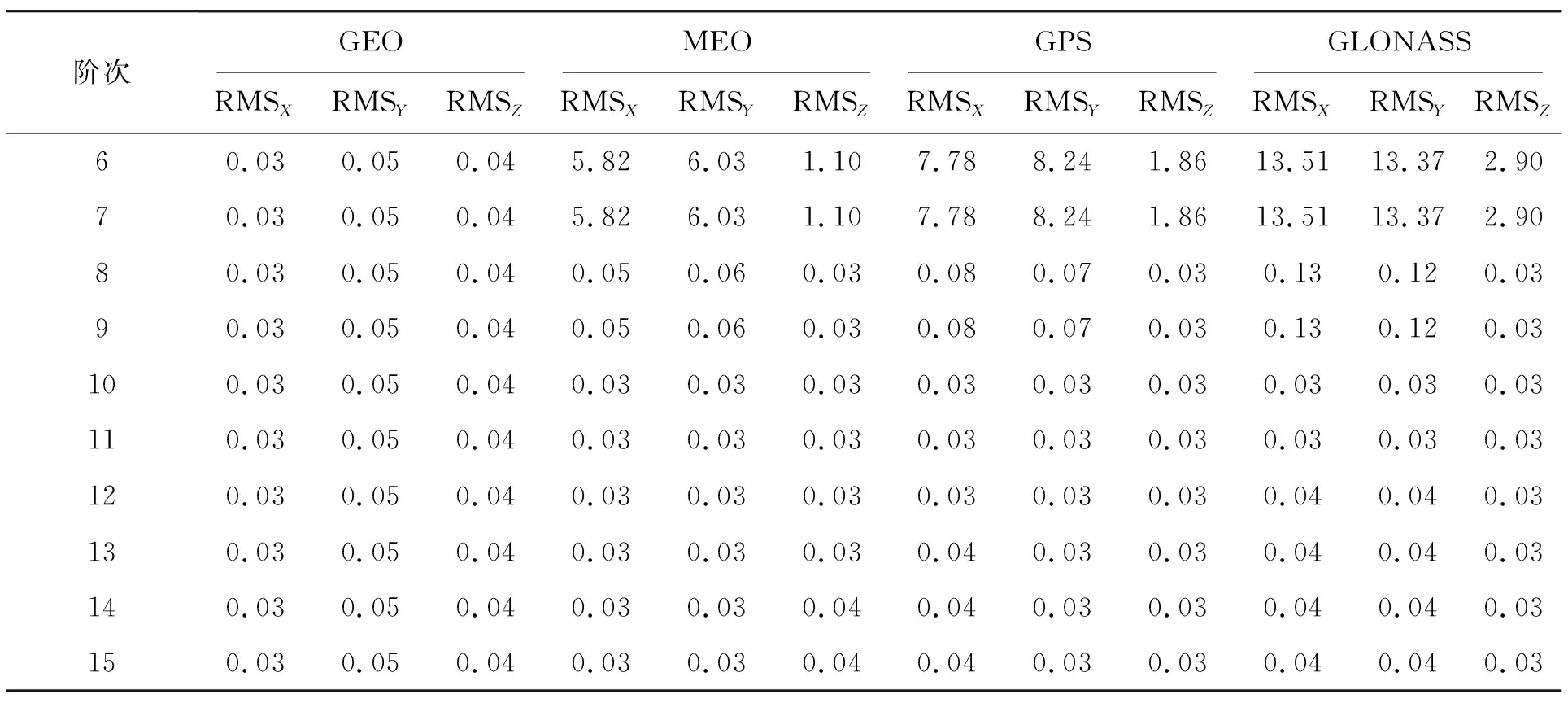
表1 四种类型卫星的不同阶次插值精度对比 单位：cm

从表1可以看到：8～15阶切比雪夫多项式均实现四种类型卫星精密星历的准确插值,三个方向上最弱RMS为0.13 cm,满足精密星历的使用要求;从6～10阶,切比雪夫多项式的插值精度逐渐提高,从12～15阶,切比雪夫多项式的插值精度缓慢下降;相同阶次的切比雪夫多项式在四种卫星的X、Y、Z方向的精密星历插值精度不一,Z方向上的插值结果明显优于其他两方向的插值结果;在低阶切比雪夫多项式精密星历插值中,GEO卫星的插值结果更加稳定,MEO卫星和GPS卫星的插值结果次之,GLONASS卫星的插值结果最差。

2.2 精密星历插值

利用本文方法对四种类型卫星采样间隔为15 min的精密星历数据进行插值,阶次取n=10,并将其结果与同阶次的切比雪夫多项式插值结果进行对比,最后2 h的插值结果如图1所示,图中虚线表示10阶切比雪夫插值多项式插值结果,实线表示10阶附有限制条件的切比雪夫多项式插值结果。

图1 10阶次两种算法插值残差图

从图1可以看出：附有限制条件的切比雪夫多项式对四类卫星精密星历插值中的龙格现象均有一定的改善作用;在GEO卫星Y方向、GPS卫星X和Y方向、GLONASS卫星Y方向的最末端,附有限制条件切比雪夫插值误差大于5 cm,但较传统的切比雪夫多项式插值结果更加稳定。

3 结束语

针对传统精密星历插值方法普遍存在的龙格现象,本文通过构造限制条件,与切比雪夫多项式组成附有限制条件的切比雪夫多项式插值方法,详细研究了附有限制条件的切比雪夫多项式的误差模型、求解过程。通过混合广播星历提供的精密星历数据,分析了不同阶次的切比雪夫多项式的插值精度,确定了切比雪夫多项式的最佳阶次为10阶;对比分析附有限制条件的切比雪夫多项式与传统切比雪夫多项式的插值效果,验证了附有限制条件的切比雪夫多项式对历元末端的龙格现象具有很好的改善作用。