结合逻辑与数学规划的交叉口动态车道功能划分优化方法
韩斅博,赵 靖,姚 佼,张范磊
(上海理工大学,上海 200093)
0 引言
在城市车道交叉口中,不同功能的车道划分对交叉口空间资源的有效利用有很大影响,仅通过信号优化来优化资源配置的效果较为局限。同时交叉口车道功能动态控制优化结果的准确性与最优化计算速度两者往往不能很好的调和。因此本文从研究分析对象的合理界定、优化目标的选择问题以及管理优化算法的简化三个发展方面着手,建立了交叉口车道功能动态划分的优化建模方法,保障了体系优化结果准确性以及模型求解的效率。
1 研究综述
1.1 交叉口静态车道功能划分
王茜(2003)提出了交叉口车道功能划分的三个步骤:(1)确定以遵循交通能力需求的原则进口的道路数量;(2)以各流向流量平均分配为原则,划分车道功能;(3)确定出口车道数,遵循出口车道数匹配原则。该研究基于研究人员可对交叉口横断面进行调整,对于交叉口横断面宽度固定的情况,即进出口道总数为定值,为了尽可能地追求最优解。
1.2 交叉口动态车道功能划分
梁潇(2008)分析了设置动态车道功能的交叉口基础条件,提出了基于检测数据的动态车道功能控制算法。该方法放弃了以往较为普遍的(非)线性规划优化方法,而采用一系列逻辑判断,作为可变车道控制的判断因素,算法简洁实用。但是该研究成果不适用于进口道可变车道较多的情况,优化结果也不能使交叉口的整体运行效率最优。
1.3 综合评述
综上所述,现有的研究主要以整个交叉口为研究对象,将车道功能划分方案与信号控制方案相结合,建立了组合优化模型。而对于动态车道功能划分的相关研究,现有的相关研究尽可能对控制算法进行简化以加快模型计算速度,同时,这种研究主要集中在单一进口,交叉口整体运行效率难以保证最优。
为了能够保证模型进行优化研究结果的准确性及模型求解的效率和实用性,本研究将从以下几个方面进行探讨:(1)研究对象;(2)优化目标;(3)模型算法,以满足动态控制的需求。
2 研究对象
以往的研究一般以一个进口道或将整个交叉口作为研究对象,导致模型优化结果不是整个交叉口的最优效果。对此,本研究提出以“进口车道组”为研究整体,本研究根据实际情况可按单个进口、对向两个进口和整个交叉口分别作为一个进口车道组,进行车道功能设计。下面给出进口分组的依据:(1)当进口车道各流向在相同相位内放行且相互间没有冲突时,将该进口作为一个进口车道组;(2)当进口道各流向不在同一相位内通行,或虽在同一相位内通行但存在冲突流向时,将该进口与相关进口一同作为一个进口组。
表1给出了五种常用的进口分组。其中,方案A至方案D表示信号相位分别采用对称放行、双环放行、单口放行、左转许可相位的情况,方案E表示信号相位也作为优化变量,在优化算法中随车道功能一同优化。

表1 典型进口组划分
3 优化目标
针对动态车道功能的特点,本研究采用关键流量比之和最小为模型优化的目标,主要原因有以下两点:(1)从动态控制实时性考虑,若以最终的控制目标为车道功能划分的优化目标,则必须对车道功能划分和信号控制方案同时优化求解,模型运算所需时间较多,不能达到实时控制的效果;(2)从车道功能划分与信号控制两者作用考虑,由于车道功能的变化会对交通运行产生一定影响,因此车道功能不宜频繁变动,主要适用于供给、需求关系发生明显变化的情况,对于一般的道路交通需求波动可采取信号优化方案来调整。若以最终的控制目标为车道功能划分的优化目标,则信号配时优化目标受制于车道功能划分,不利于信号控制的动态调整。
4 模型算法
本研究采用非线性规划与逻辑判断相结合的优化方法,首先确定可变车道所在进口,然后选择信号相位方案,再根据所对应的车道功能优化算法进行优化,最后输出车道功能划分方案及信号相位方案。
模型的逻辑流程和具体的算法流程分别如图1和图2所示。

图1 逻辑流程

图2 算法流程
图2各式含义如下所示:
式(1)表示目标函数,进口组关键流量比之和最小;式(2)、式(14)、式(20)表示进口道车道数约束;式(3)至式(5)、式(15)表示确定各相位关键流量比约束;式(6)、式(24)表示直行与右转流量比之比允许范围的约束,即允许右转流量比适当大于直行流量比;式(7)、式(25)表示直右车道中右转车比例允许范围的约束,即当直右车道中右转车比例较高时采用右转专用道;式(8)、式(26)表示右转流量比约束,即若为直右车道,右转流量比应与直行流量比相同,否则应为右转专用道;式(9)、式(18)、式(27)表示非负性和整数的约束;式(10)至式(11)表示判断关键流向是否属于同一进口并且非关键流向是否存在可变车道;式(12)表示确定非关键流向所属进口;式(13)表示目标函数,对应流向流量比匹配性最好;式(16)至式(17)表示各流向非关键流量比应小于关键流量比的约束;式(19)表示目标函数,进口组关键流量比之和最小;式(21)至式(23)表示关键流量比约束;式(28)表示按流量分配车道功能;式(29)表示判断有无固定左转功能的车道在直行车道右侧;式(30)表示设置保护型左转相位的判断条件1:左转车道条件;式(31)表示设置保护型左转相位的判断条件2:最小交通量条件;式(32)至式(33)表示设置保护型左转相位的判断条件3:最小乘积条件;式(34)至式(35)表示确定各可变车道功能。
图2各参数含义:
Y表示进口道组关键流量比;y表示左转相位关键流量比;y表示直行相位关键流量比;n表示i进口j流向车道数,j=1表示左转,j=2表示直行,j=3表示右转;m表示i进口j流向固定车道功能的车道数;α表示i进口道车道数;β表示i出口道车道数;y表示i进口j流向流量比;δ表示右转专用车道系数,表示直行与右转流量比之比大于δ是允许的,默认值可取0.7;γ表示右转专用车道系数,表示直右车道中右转车比例大于γ时,采用专用右转车道,默认值取0.8;DL表示i进口可变车道的集合;S表示i进口j流向饱和流率;Γ表示i进口固定功能的车道k对于j流向是否允许,允许为1,不允许为0;Δ表示i进口可变车道k对于j流向是否允许;q表示i进口j流向交通量;ε表示左转交通需求与对向直行交通需求乘积的检验系数,当对向直行车道数为1时,取50 000,当对向直行车道数为2时,取90 000,当对向直行车道数为3时,取110 000。
5 算例分析
本文选用Wong研究中的算例来对模型计算准确性、实时性和适用性进行检验。为便于讨论,后文饱和流率和延误计算模型均采用原文中的计算方法,分别如式(36)和式(37)所示。

式中:S表示i进口k车道的饱和流率;S表示i进口直行车饱和流率;P表示车道k中从i至j流向车流的比例;r表示转弯半径。

式中:D表示i进口k车道的延误;C表示信号周期;u表示i进口k车道的绿信比。
交叉口几何设计和交通条件数据分别如表2和表3所示。原文分别采用割平面法和启发式线性搜索算法进行求解,其车道功能划分优化方案与本文计算结果对比如表4所示。通过本算例分析可得:(1)本文建立的模型能保证车道功能划分结果的准确、实时性;(2)相较“基于车道的信号控制优化方法”模型复杂程度大大降低;(3)优化计算时间大大减少;(4)由于目前较为常用的Webster或HCM延误计算公式均为非凸函数,直接将其作为车道功能划分的优化目标可能导致优化结果为局部最优解,本文模型中将优化目标定为关键流量比之和最小,一方面可使优化结果为全局最优解,另一方面也可使信号控制方案更为灵活,不受制于车道功能划分。
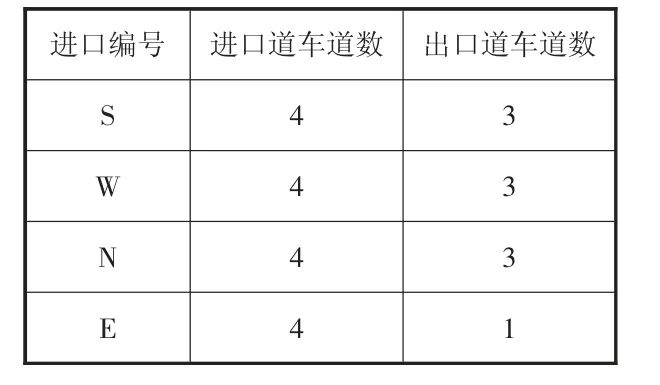
表2 交叉口几何条件

表3 交叉口交通需求条件
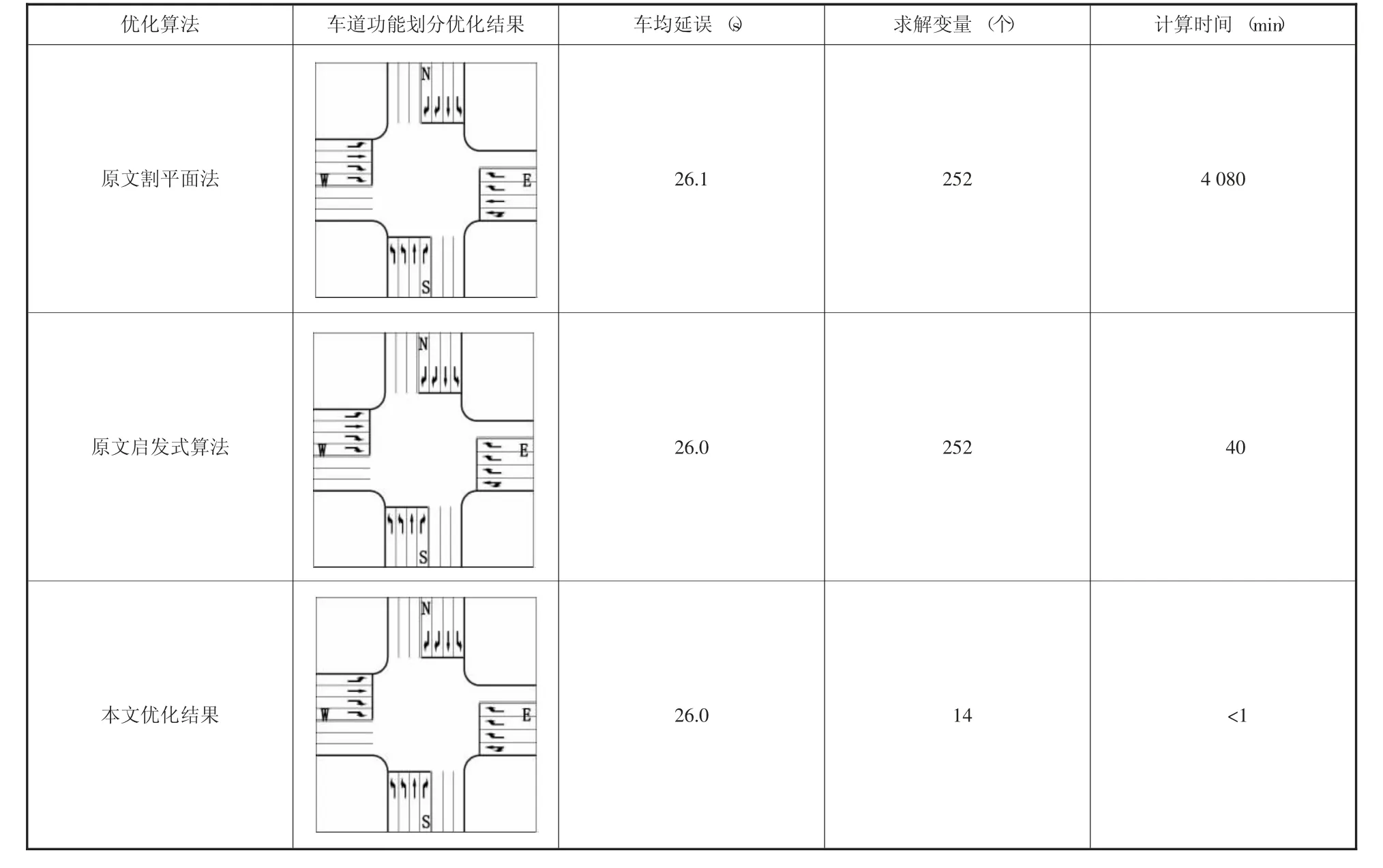
表4 算例计算结果
6 结论
本文提出了适用于动态控制的车道功能划分优化方法主要得出以下几点结论:(1)将“进口车道组”作为研究对象,可在保证优化结果准确性的基础上,简化模型,提高了求解效率,满足动态优化的要求;(2)将关键流量比之和最小作为优化目标,提高了模型求解准确性和求解速度,满足动态优化的要求,不受制于车道功能划分;(3)采用非线性规划与逻辑判断相结合的优化方法,能提高模型的计算效率,提供管理者更多的选择空间。

