基于偏序集改进型SMCDM的供应商选择研究

胡英达 （辽宁工程技术大学 工商管理学院，辽宁 葫芦岛 125105）

0 引 言

对于决策者，做出正确的决策是一项具有挑战性的工作，由于早期阶段存在很高的风险和不确定性，期间做出的决策具有很大的不可靠性。有研究针对该问题提出通过使用“分层概念”来提高可靠性，它描述了一个系统，考虑多个情境下的若干状态，即考虑未来可能发生的事件会影响决当下决策的正确性，因此应在决策之前充分考虑可能会产生的影响情况，以提高决策的准确性，对此提出可以使用分层多准则决策方法（SMCDM）来解决。

应用SMCDM计算问题结构如下：活动被认为是通过不同状态的系统过度，事件被认为是输入，事件影响的指标权重被认为是输出。该方法决策时充分考虑了各种可能产生影响的情况，但需要决策者做出大量的假设，如假设事件的发生、假设事件发生的概率，就实际情况而言，很难做出准确的假设；面临着指标精确赋权的难题；最后，由于考虑的条件众多，需要针对各情境进行大量运算等难题。

本文针对提出的SMCDM，运用偏序集进行优化。研究表明，应用偏序集已经改进优化了多种决策方法。岳立柱等提出了能够处理权重的偏序多准则决策方法，该方法在指标集结过程中，用权重空间代替权重向量，只要权重大小顺序排序即可，而且只要顺序不发生变化，偏序结构保持不变，提高了结果的鲁棒性。理论上只要以权重作为指标集结手段，则能够应用偏序集予以表达。传统SMCDM需要分析各情境发生的概率，及各情境下指标的精确权重，增加了工作难度。因此，为解决不同情境下多种权重问题，应用偏序集予以解决，从而降低工作难度，同时提高鲁棒性。

1 研究综述

1.1 供应商选择

供应商选择是企业保持战略竞争地位的关键问题。供应商通常具有自身的长板与短板，因此很难在不使用MCDM方法的情况下客观地选择最佳供应商，使用合适的模型进行选择成为管理者面临的挑战。

多种方法被广泛地应用于供应商选择，刘彬等从绿色采购出发，提出环境因素作为供应商选择评价指标体系的重要内容，运用AHP对供应商选择进行模糊评判。Giannakis等运用ANP，考虑可量化和易获得的可持续发展相关评价指标，建立了可持续性供应商选择的绩效衡量框架，完善了量化决策过程。Abdullah等提出了在标准偏好函数下使用PROMETHEE的绿色供应商偏好，选择了7个经济指标，检查不同偏好功能对最终的影响，得出了可比较的结果。袁宇等针对供应商选择决策中评价值为混型信息、决策者权重和准则权重难以确定的问题，提出权重信息未知情境下的、基于信任度函数和熵权变换的MCGDM方法，针对混合类型评价信息的不可公度性，采用混合型VIKOR方法构建供应商选择评价模型。Cheraghalipour针对农具行业供应商，选择8个指标构建评价体系，用BWM方法确定指标的权重，然后结合BWM和VIKOR方法对候选供应商进行排序。马书刚等从合作弹性、运营弹性、信息弹性、绩效水平4个维度构建制造企业供应商评价指标体系，运用熵值法确定指标权重，在考虑到现有评价方法缺乏有效验证的基础上，将TOPSIS和案例推理方法相结合，对制造企业供应商的弹性与绩效水平进行评价分析。以上方法均需计算精确权值，但不同方法容易使权重不具稳健性，造成结果偏差。

1.2 分层概念发展、应用

分层概念（CST）是Zadeh引入并发展的创新概念，是分层的一种形式。CST描述了为了达到目标状态，通过具有相关联的输入和产生输出进行状态转换的系统，目标状态是一组初始状态，各状态基于它们与目标集合的距离被递增的分层，然后系统地识别目标周围的环境，并且使用“增量目标放大”的概念逐渐构架目标周围的层。

分层概念与以前的分层逻辑、方法、编程、分析和其他等分层的版本和应用相比，这个新版本的分层可以处理各种问题，也相对容易应用。Asadabadi等首次应用该概念，在物流信息系统建模中运用CST，构造了信息优势和契约中的需求诱导实例，展示了该概念在物流、信息学和合同方面的应用，并协助建模过程，但是在物流信息系统建模中运用CST不能考虑不同重要性的目标。针对这一不足，开发了一种算法，并通过实例运用该算法在大学附近选择吃午餐的最佳位置进行说明。研究者利用谷歌地图数据进行选择时考虑了两个目标——“最短距离”和“最高评价”，对这些目标进行不同的赋权，利用提出的算法确定最佳餐厅。

2 分层多准则决策

Asadabadi等发现CST和MCDM方法相结合的潜力，提出了一种新的多准则决策方法，即SMCDM，虽然没有利用CST所有的功能，但是使用了主要概念来分层决策环境。在运用SMCDM方法时，决策所处的环境是分层的，使得通过考虑近期可能发生的事件来做出决策。

假设有n个指标和m个样本，备选方案a至a根据标准c至c进行比较。然而，属性的权重ω（ i=1,2,…,n）取决于当前情况是否继续发生。考虑到该决策是一个当前处于W状态的系统，假设有h不同的状态，包括当前的状态，该决策可以处于或过渡到。状态是可能发生的事件的结果，并将系统带入不同的状态。这样，系统可以移动到h±1状态，而不是当前的状态，则每种转态下的指标权重可能会发生变化，详情见文献[2]。

3 偏序集相关理论

根据文献[18]定理1可用矩阵来表示，及给定上三角矩阵E：

当ω≥ω≥…ω≥0，上三角矩阵E和X进行如下运算，得到矩阵D：

矩阵D中若第i行小于第j行，由此构造偏序关系。由指标集构造偏序关系最常见的方式如下：

根据偏序关系，可以对方案进行两两比较，并建立如下偏序关系矩阵R=（r），其中：

其中：I为单位矩阵，运算符*为布尔乘法,根据H可以绘制Hasse图。

应用偏序集进行分层多准则决策步骤：

Step1：依据指标个数（n）及权重大小，排出所有指标权重顺序关系，共有n!种排序情况，根据实际情况选出其中d种顺序，得到决策矩阵A（ i=1,2,…,d）,对决策矩阵B的数据进行归一化处理，得到矩阵X；

Step4：由式（3）得到偏好关系矩阵R；

Step5：由式（4）得到Hasse矩阵，并绘制Hasse图，对方案间的排序和结构关系进行分析；

4 案例应用

本案例数据和指标来自文献[2]和文献[19]。案例中，事件指的是可能发生并且影响指标权重变化的事件，多丽丝·帕尔斯公司是伊朗一家卫浴设备和配件批发商和制造商，在供应商选择时考虑3项指标：质量、价格和供货。

近期将有三种事件可能发生，即“与X公司签订新合同”、“与Y公司签订新合同”和“拥有新投资者”，不同事件的发生，将导致指标权重发生变化。例如，如果与X公司签订了合同，那么价格将变得不重要，即质量、价格和供货权重：（0.52,0.11,0.37）。表1列出了可能的8种情况下指标的权重。

表1 不同事件下指标的权重

Step1：选取文献[22]中供应商相关数据，质量用产品的不合格率表示；供货用未按时交货率表示，数据如表2所示。

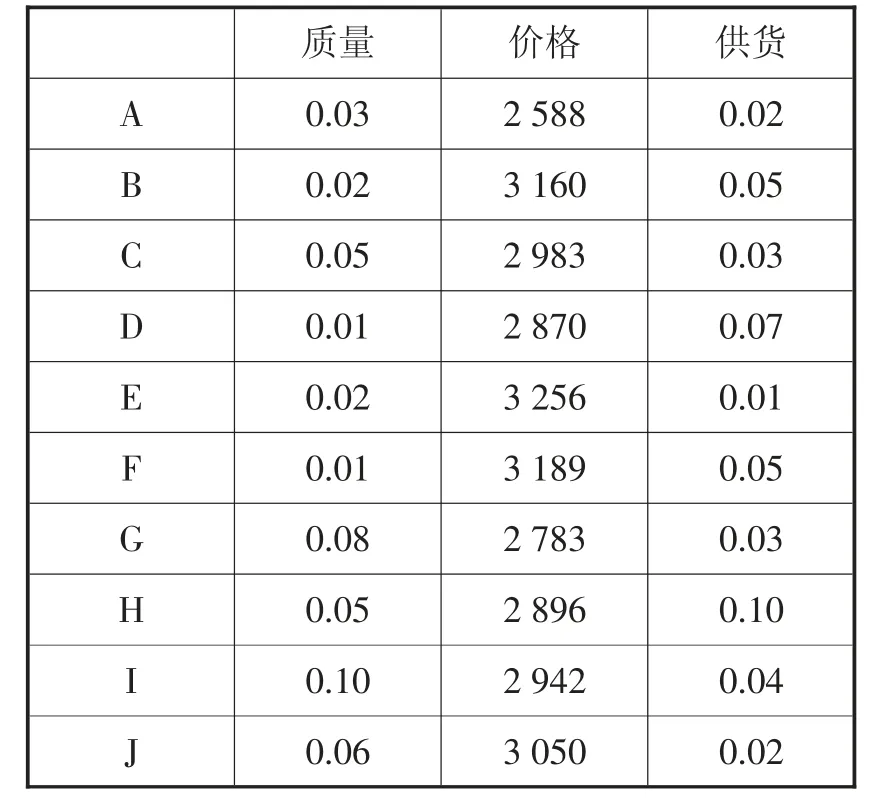
表2 供应商原始数据

采用最大最小值法对数据进行无量纲化，其中价格为成本指标，转换为效益指标，结果如表3所示。

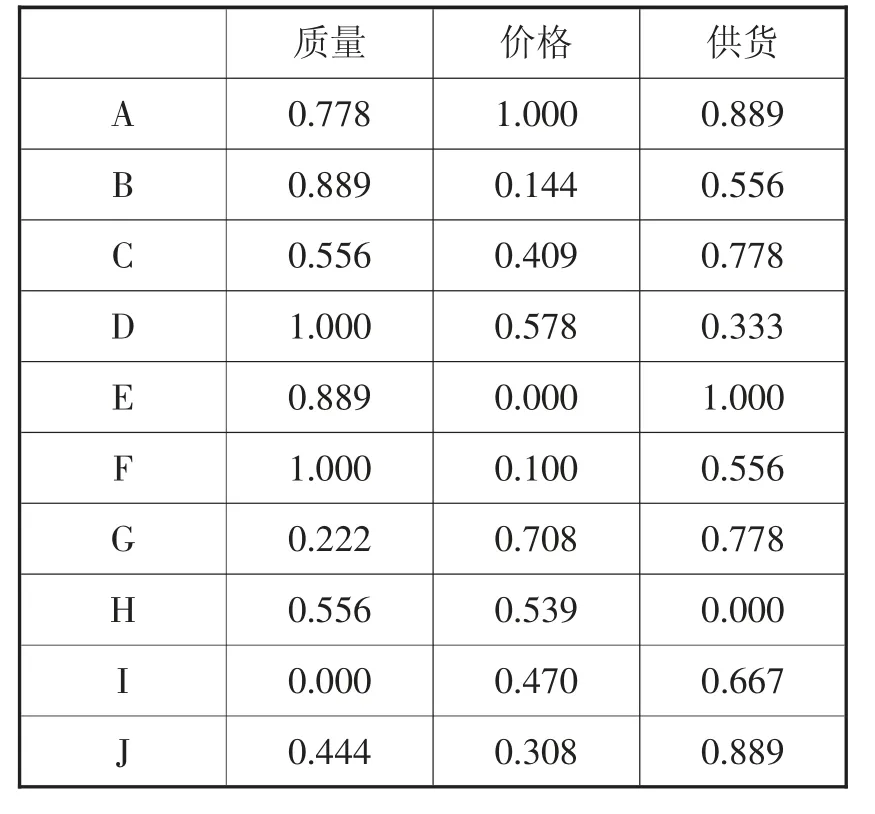
表3 原始数据归一化

Step2：案例中8种转态下的指标权重顺序可分为3类：

编号2和编号8试验的校正误差如图8所示。由图8可知，训练集和测试集的最大误差分别为0.09 mm和0.10 mm，表明网络对训练样本和测试样本具有同样精准的预测效果，也验证了训练集与测试集选择的合理性和科学性。由于两个RBF网络的结构相同，均具有5个隐含层神经元，因此两次训练结果的误差分布趋势相近，而两次优化得到的网络参数不同，所以两个网络的误差分布不完全重合。但两个网络的误差曲线都表现出相同的波动特性，这与RBF神经网络的局部逼近能力有关。与某一神经元隐含层节点中心具有特定距离的样本，其校正误差较小；而其它偏离该位置的样本，其校正误差将偏大。

①供货≥价格≥质量，指标间依权重大小从左往右依次降序排列，得到决策矩阵，如表4所示。

表4 决策表

②供货≥质量≥价格，步骤同上。

③质量≥供货≥价格，步骤同上。

Step3：根据式（1）对①类各个评价指标下的数据进行累加，得到累加变换矩阵，如表5所示。

表5 累加变化

②、③类累加变换步骤同上。

Step4：对累加变换矩阵进行行向量的两两比较，若第i行向量大于第j行向量，则有r=1，否则r=0，根据式（3）得到偏序关系矩阵R（如表6所示）。

表6 偏序关系矩阵

②、③类偏序关系矩阵步骤同上。

Step5：根据式（4）将偏序关系矩阵R转换为Hasse矩阵H并绘制Hasse图（如图1所示）进行分析。

图1 Hasse图

②、③类偏序关系矩阵计算步骤同上。

通过Hasse图对①类情况进行如下分析：

（1）从图1中可以直观地看出各样本间的分层和聚类信息。偏序集理论具有上集研究案例优于下集研究案例的特点（如A指向C，表示A优于C）且具有传递性。因此图1中，越是位于图上端的节点群体表示供应商更优，可见10家供应商被分为四个层集。A和E供应商最优，位于最底层的H供应商最差。层集越多，说明方案间的差异越大，且同层之间的方案不可比。

（2）体现分层信息，在8个场景下的3种权重排序中，第一层集不尽相同，恰恰说明了，不同场景下，最优供应商不同。A、E供应商在第一层集出现3次，D供应商在第一层集出现1次，F供应商在第一层集出现1次。A、E供应商均在第一层集，说明A、E供应商相较于其他供应商更稳健、更优。

（3）体现稳定程度，如A优于C，C优于B，B优于H，只要同场景下各指标权重排序不变，则10个供应商的排序结构不变，无论权重大小怎么变动，原可比关系不变，充分说明了偏序集评价的稳健性。

如果Hasse图展示的结果不能满足精度要求，根据文献中求解秩均值方法依旧可以实现全排序，结果为A＞E＞C=G＞J＞D＞F＞I＞B＞H。

②类、③类步骤同上。

5 结 论

本文运用偏序集方法对10家供应商进行评价，通过偏序集解决当前多场景多准则决策中需要对每种场景下的评价指标精确赋权的难题。本文提出只需根据指标数量及实际情况，对各场景下的权重依据大小进行排序分类，即只需通过各场景下的获取的指标权重顺序信息即可，减少了计算量，简化了决策过程，且更具稳健性。本文从研究方法的视角探讨供应商评价，为企业通过偏序集方法对供应商评价提供了理论方法与研究手段，丰富了企业供应商评价方法的研究成果。

基于本文的研究成果，运用偏序集评价方法较为精准地将各供应商进行分层聚类，有利于企业准确选择更加完善的供应商，为公司创造更大的经济效益。