澳大利亚RMFII项目中“统计推理”的引介与思考

高 翔

澳大利亚RMFII项目中“统计推理”的引介与思考

高 翔

（南京信息工程大学 教师教育学院，江苏 南京 210044）

“统计与概率”是重要的数学学习领域，其测评与教学成为近年来研究的热点问题．通过引介澳大利亚“重塑数学的未来II（RMFII）”项目中“统计推理能力”的相关内容，以期为中国“统计与概率”的研究与教学提供借鉴．运用文献研究、历史梳理、案例研究等方法呈现了“统计推理能力”的测评思路，回溯“统计推理8‘地带’学习进程”的构建历程，结合具体的案例分析该学习进程在“定位”学生统计推理能力水平和“链接”教学建议方面的举措；给中国“统计与概率”的研究与教学带来3点启示：进一步细化“数据分析素养”的水平要求，增强可操作性；开发测评任务，探索适应中国学生的统计与概率学习进程；建设丰富的教学资源库，提升教师专业发展．

统计与概率；澳大利亚；RMFII项目；统计推理；数据分析素养

1 问题提出

在中小学阶段，与传统的代数和几何内容相比，统计与概率在数学课程中出现的时间较晚，却在近10年来引起了数学教育研究者的极大关注，相关研究的数量呈现出指数级增长的趋势[1]．中国也在《普通高中数学课程标准（2017年版）》中提出学生应当具备“数据分析素养”，即能“针对研究对象获取数据，运用数学方法对数据进行整理、分析和推断，形成关于研究对象知识的素养．数据分析过程主要包括：收集数据，整理数据，提取信息，构建模型，进行推断，获得结论”．

国外的相关研究较少提及“数据分析素养”[2]，主要围绕统计素养（statistical literacy）、统计推理（statistical reasoning）等[3]展开研究．国外研究者大多将统计素养视作未来公民需要具备的“基本统计知识、统计理论方法、运用统计方法解决现实问题的能力、对统计的信仰、态度和批判性等”[4–5]，这些内容较中国的“数据分析素养”内涵更为上位，而以变异性（variation）为核心的统计推理能力，与中国“数据分析素养”则有更多相近之处．国际著名统计教育专家本–兹维（Ben-Zvi）和加菲尔德（Garfield）将统计推理能力的描述性定义界定为“学生能运用统计的观点进行推理，理解与统计相关的信息，能将数据和可能性的相关观念加以联系，理解和解释统计过程并解释统计的结果”，将统计推理能力的操作性定义界定为“学生能描述数据的呈现、整理与简化数据、表征数据、分析和解释数据”[6]．

统计推理能力的描述性定义与中国普通高中数学课程标准中“数据分析素养”的内涵虽然在表述顺序上略有不同，但都体现了“对数据进行整理、分析、推断，从而加深对数据的认识”，统计推理能力则更加强调将数据和可能性的相关观念加以联系、深刻理解统计全过程和最终结果，中国课程标准则强调通过数据分析，加深对研究对象本身的理解．统计推理能力的操作性定义与“数据分析素养”中“数据分析过程”也基本一致，因此对统计推理能力的相关研究可以为中国的数据分析素养研究以及统计与概率的教学研究提供借鉴．

如何评测学生的统计推理能力？研究者们从变异性角度构建了一些统计推理能力框架，如本-兹维（Ben-Zvi）的变异性推理阶段框架[7]，里德（Reid）和雷丁（Reading）的变异性推理层级框架[8]，诺尔（Noll）和尚尼斯（Shaughnessy）的学生变异性推理的概念格[9]等，但这些框架只适用于特定的统计与概率内容，比如抽样、数据的分布等，那么有尽可能覆盖中小学“统计与概率”内容的统计推理能力框架吗？这是研究者们亟需思考的第一个问题．

如何针对不同统计推理能力的学生进行教学？国外研究者进行了一些探索，而中国的许多教师因为“统计的内容在中小学出现的时间不长”，“教师对很多内容的理解不深刻”[10]，“不清楚统计教学的阶段性要求”[3]等原因，很难实施有针对性的教学，这是摆在一线教师面前的另一个棘手问题．

针对统计推理能力的框架构建和相关教学实施问题，澳大利亚重塑数学的未来II（Reframing Mathematical Futures II，以下简称RMFII）项目中的“统计推理研究”给出回应．

尝试引介RMFII项目中统计推理的相关研究，分析其在测评学生统计推理能力和指导实际教学中的应用，并基于该项目为中国统计与概率的研究与教学给出几点思考．

2 RMFII项目概述及统计推理框架演变进程梳理

重塑数学的未来II（RMFII）是由澳大利亚皇家墨尔本理工大学的戴安娜·西蒙（Dianne Siemon）教授主持的澳大利亚数学与科学合作计划（Australian Mathematics and Science Partnership Program，AMSPP）项目，历经5年（2014—2018），共有32所澳大利亚中学，近八十名教师和约三千五百名七～十年级的学生参与．该项目的主要目标是构建一个可持续的、基于证据的学习和教学资源，以支持七～十年级学生数学推理能力的发展[11]．该项目中的数学推理能力主要包括代数推理、几何推理和统计推理3个分支，这里主要引介统计推理分支的相关内容．

RMFII项目统计推理的研究思路包含了以下5个阶段：（1）通过文献分析，初步确定学生统计推理的“假设学习轨迹（hypothetical learning trajectories）”；（2）开发、试验和验证统计推理测评任务；（3）使用Rasch分析方法，识别统计推理的“大观念（big ideas）”，确定学生初步的学习进程（learning progressions）；（4）运用设计研究的方法对统计推理测评进行迭代，从而确定学生最终的学习进程，同时开发教学建议；（5）观测学生的进步[11]．

RMFII项目统计推理研究的负责专家是澳大利亚塔斯马尼亚大学的简·沃森（Jane Watson）教授．简·沃森教授长期致力于中小学阶段统计与概率教学、学生统计素养测评的相关研究，RMFII项目中统计推理的相关测评任务基本沿用了简·沃森教授近30年来的研究成果．同时RMFII项目中统计推理的8“地带”学习进程框架是在简·沃森团队前期统计素养6水平层次框架和统计素养8成分6阶段层次框架的基础之上逐步发展而来，具有高度的连续性，因此，首先对RMFII项目统计推理的框架演变进程进行梳理．

2.1 学生统计素养的6水平层次框架

简·沃森团队于1993、1995、1997和2000年对澳大利亚塔斯马尼亚的3 852名三～九年级的学生进行了统计素养的测评，简·沃森团队将统计素养界定为“学生能在不熟悉的情境中，联系统计与概率课程中的相关概念、调用数学的术语、统计的技能，逐步体会变异性”[14]．简·沃森团队运用Rasch分析方法，对80道测评试题进行分析，确定了统计素养的潜在结构和6个理解水平，从低到高依次为特质的（idiosyncratic）、非正式的（informal）、不一致的（inconsistent）、一致非批判的（consistent non-critical）、批判的（critical）、批判的数学的（critical mathematical），具体表述如表1[12]所示．

表1 统计素养层级

在该统计素养的层级框架中可以看到一些统计推理的影子，如水平5不要求学生运用比例推理，只需运用定性的方式解释可能性，感受变异性；水平6则要求学生能在媒体情境或随机现象情境中使用比例推理，在感受不确定性的同时做出预测．但统计推理的相关内容还没有从统计素养的研究框架中“剥离”出来，简·沃森在该阶段的研究为RMFII项目中的“统计推理”打下了基础．

2.2 学生统计素养8成分6阶段层次框架

简·沃森在2006年的专著《学校中的统计素养：发展与目标》（）中进一步阐述了统计素养的8个重要成分：情境（context）、抽样（sampling）、表征（representation）、平均数（average）、可能性（chance）、推断（inference）、变异性（variation）、数学/统计技能（math/stat skills），并将原来的统计素养6水平层次框架（表1）进一步细化为8成分6阶段层次框架，如表2[13]所示．

统计素养的8成分6阶段层次框架中蕴涵了更多“统计推理”的要素，如在抽样和表征的较高阶段，推断和变异性的大部分阶段都对统计推理提出了要求，但仍可以发现有些阶段的表述不够明确，如“推断”的阶段5仅较阶段4发生细微的变化，“变异性”的阶段6和阶段5的表述是一致的，这些都会在实际操作的时候带来一些模糊的地方，这些问题的存在进一步推动了RMFII项目中“统计推理”的相关框架的修改与构建．

2.3 RMFII项目中统计推理的8“地带（zone）”学习进程

基于学生统计素养的8成分6阶段层次框架，简·沃森团队从“大观念”的视角重新加以组织，确定了以变异性（variation）为基础，期望与随机性（expectation and random- ness）、分布（distribution）、非正式推断（informal inference）3个“大观念”为重要组成部分的统计推理框架[14]．通过对参与RMFII项目统计推理测试的一千五百多名七～十年级学生的作答进行Rasch分析，初步确定了七～十年级学生统计推理的学习进程原型，通过设计研究的多轮迭代之后，最终确定了学生统计推理的8“地带”学习进程，如表3[14，15]所示．

RMFII项目中统计推理8“地带”学习进程紧紧围绕期望与随机性中的变异，分布中的变异和非正式推断中的变异这3个“大观念”进行了学生统计推理学习进程的划分，行为样例也依据这3个“大观念”进行了举例．统计推理8“地带”学习进程是基于简·沃森团队在过去近30年来的相关研究得出的最新成果，一脉相承，为定位学生统计推理学习阶段和教师的教学提供了坚实的理论支撑．

3 RMFII项目中统计推理8“地带”学习进程的应用

RMFII项目中统计推理8“地带”学习进程的应用主要表现在两个方面：第一，确定学生在统计推理测试中的表现最终落在学习进程的哪个地带；第二，为教师提供足够的信息判断学生统计推理的现有水平，从而为其制定个性化的教学方案．以下将通过实例加以说明．

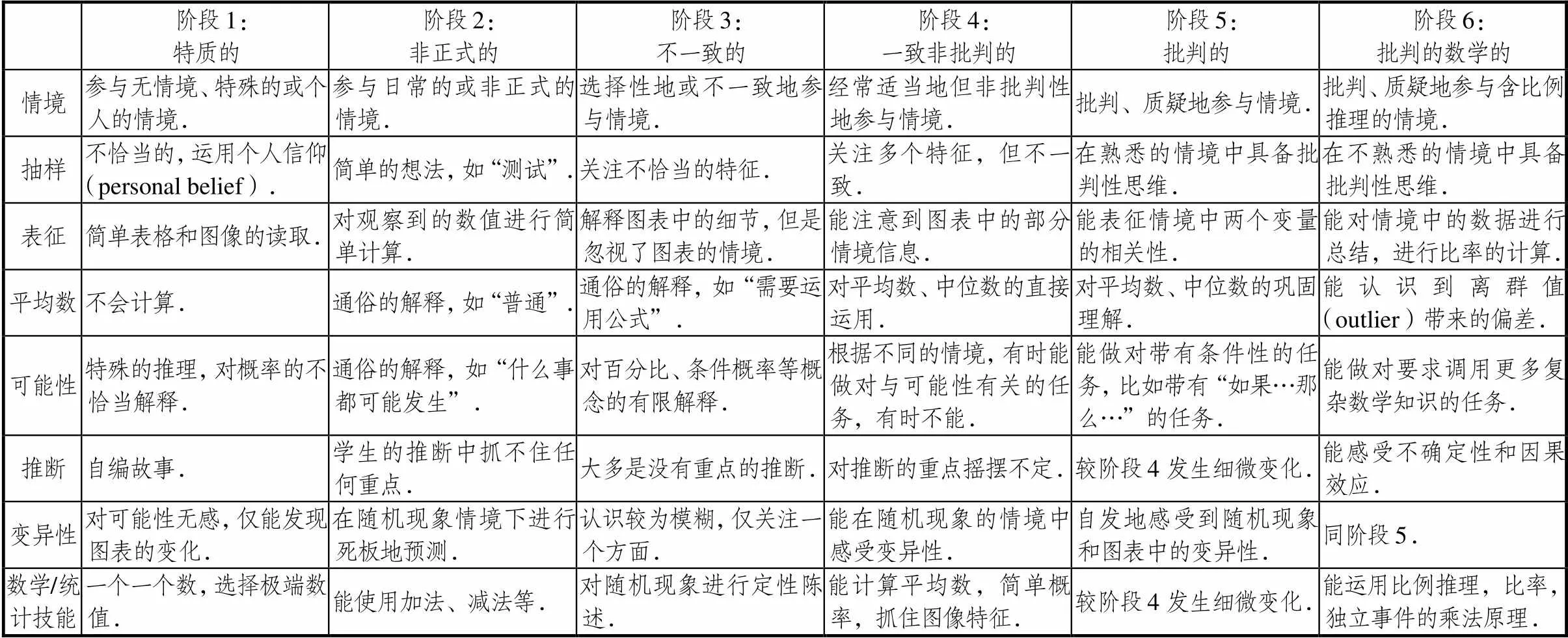
表2 统计素养8成分6阶段层次框架

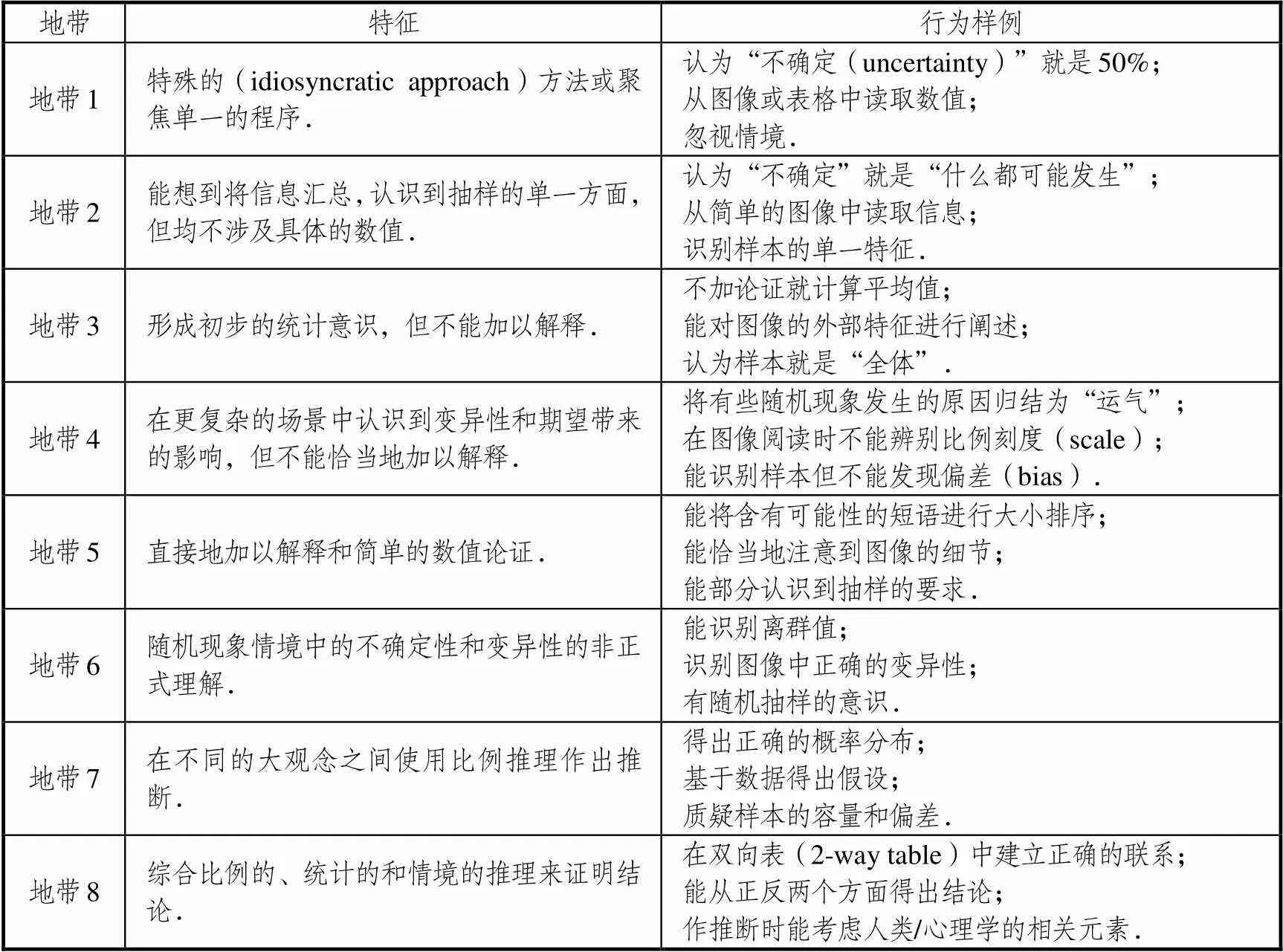
表3 学生统计推理8“地带”学习进程

3.1 依据学生测试表现定位统计推理“地带”

以RMFII项目中统计推理测试题SCON为例，测试题、学生解答及其所属“地带”以及相关的解释如表4[16]所示．

RMFII项目会将参与统计推理测试学生在所有测试题上的作答编码与相应的统计推理8“地带”相匹配，运用Rasch分析的方法，得出学生统计推理的整体水平并确定其落在统计推理学习进程中的具体位置，从而进一步统计出各个“地带”学生的人数比例分布，如参与此次RMFII项目统计推理的七～十年级学生在各个“地带”的人数比例分布如表5[14]所示．

可以看出不论哪个年级，大部分学生都落在了地带4中，即学生可以在复杂的情境中认识到变异性所带来的影响，但是不能恰当地加以解释．实际上地带5才是统计推理能力的真正起点，表明大部分学生仍然缺乏解释和论证他们统计推理的能力，为教师进行后续的统计推理教学设计提供了实证依据．

3.2 将统计推理“地带”与教学建议相链接

在确定了学生统计推理能力所处的地带后，教师会考虑这样一个问题“如果学生统计推理落在某个特定的地带，我可以提供怎样的帮助让学生上升到更高一级的地带？”RMFII项目统计推理的一个重要成果是为教师开发了一系列资源和与统计推理“地带”相匹配的教学建议．

教学建议通常由两大部分组成，第一部分为巩固与建立（consolidate and establish），试图识别学生现有的知识、技能和理解，并提出可能有助于学生加深理解的活动建议；第二部分为引介与发展（introduce and develop），具有一定的前瞻性，旨在为学生发展到更高一级的统计推理“地带”设置相关的活动和观念．表6[15]呈现了以统计推理地带4为例的教师教学建议，表中如SHSE2.1等代码表示RMFII项目统计推理测试中的测试题编号，斜体标出的是建议实施的活动名称．

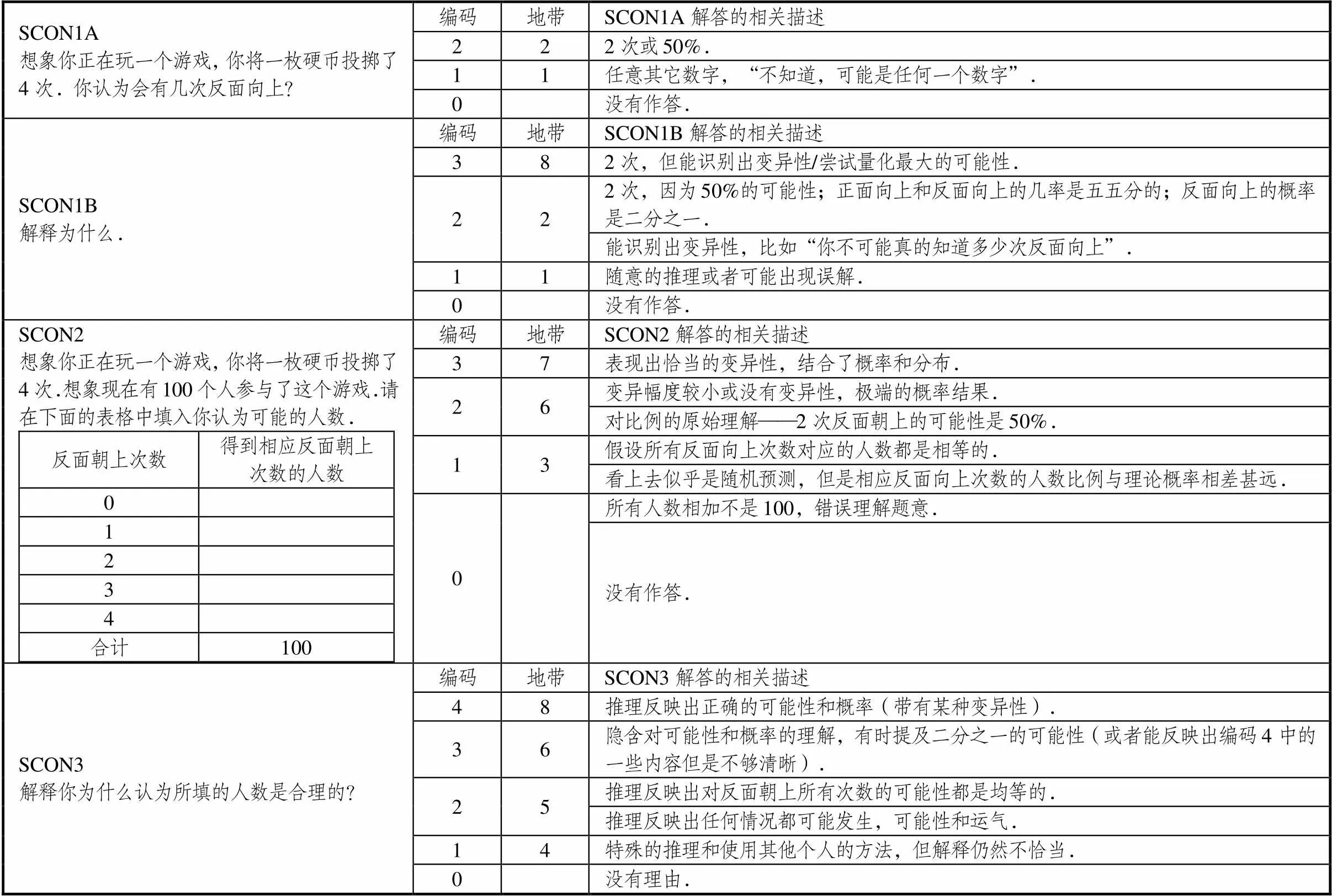
表4 样题SCON的相关信息

表5 七～十年级学生“地带”分布

教师可以通过比对统计推理学习进程中某个地带学生的行为表现，有效地定位学生目前统计推理的水平，然后依据教学的特定情境，有针对性地选择教学建议中提供的丰富活动，为学生提供个性化的水平提升方案．同时，RMFII项目提供的教学建议及其相关教学资源（如线上的统计与概率学习平台）可以供教师方便地获取并进行共享．RMFII项目也鼓励教师自主开发相关的统计推理活动或任务，以激发教师的教学热情、促进教师的专业发展．

4 思考与启示

通过引介RMFII项目中统计推理的8“地带”学习进程的构建历程、学生在测评试题中的表现与学习进程的匹配以及不同学习进程与教学建议的链接，得出对中国的统计与概率研究与教学的几点思考与启示．

4.1 进一步细化“数据分析素养”的水平要求增强可操作性

中国《义务教育数学课程标准（2011年版）》中提出“数据分析观念”，要求学生：“了解在现实生活中有许多问题应当先做调查研究，收集数据，通过分析做出判断，体会数据中蕴涵着信息；了解对于同样的数据可以有多种分析的方法，需要根据问题的背景选择合适的方法；通过数据分析体验随机性，一方面对于同样的事情每次收集到的数据可能不同，另一方面只要有足够的数据就可能从中发现规律．”这样的表述能体现出变异性为基础，让学生经历数据的整理、分析和推断过程，但不能体现不同年级、不同水平学生的行为表现，可操作性不强．中国最新修订的《普通高中数学课程标准（2017年版）》提出了“数据分析素养”，并将其划分为3个水平，但是每个水平涵盖了众多统计与概率内容，教师很难将学生具体的数据分析行为进行精准地水平定位．

RMFII项目虽然只针对统计推理的相关内容，但是其围绕期望与随机性、分布、非正式推断这3个“大观念”和变异性这条主线进行了8个“地带”学习进程的详细划分，可以更加精准地定位学生的真实水平，未来中国课程标准中对“数据分析素养”的水平划分可以借鉴RMFII项目，依据统计与概率内容中的“大观念”，针对不同年级不同层次的学生制定“数据分析素养”的水平框架．

表6 统计推理地带4教学建议

4.2 开发统计与概率测评任务探索适应中国学生的统计与概率学习进程

RMFII项目在文献研究的基础上，首先确定了学生统计推理的大致学习轨迹，然后通过大规模测评、Rasch分析的方法，确定学生统计学习进程的原型，再通过多轮迭代的设计研究方法最终确定了学生统计推理的学习进程．整个过程中统计推理的测评任务起到了非常关键的作用，一方面用来测试学生统计推理的真实水平，另一方面为构建学生统计推理学习进程原型和后续的设计研究工作提供了强有力的数据支撑．未来中国的研究者可以在相关理论的支撑下，开发更多的统计与概率测评任务，服务于今后统计与概率的相关研究．

在统计与概率的实际教学层面，由于统计与概率内容在整个教材中的课时比重小，教师只有教到相关单元时才会让学生接触统计与概率，更多时候统计与概率的内容是在“沉睡”的[3]．同时，大部分教师仍然习惯运用数学教学的方式进行统计内容的教学，但统计与概率的教学与数学教学还是存在本质上的差异[17]，因此有必要依据中国学生的实际情况构建适应中国学生的统计与概率学习进程，让教师们有据可依，针对处于不同学习进程中的学生给予不同的教学支持．因此，可以借鉴RMFII项目的研究思路，通过文献研究、任务测评、设计迭代逐步探索适应中国学生的统计与概率学习进程．

4.3 建设丰富的统计与概率教学资源库提升教师专业发展

RMFII项目统计推理的负责人简·沃森在过去的30年中累积了数以百计的统计与概率测试任务，并在其大量的研究论文附录中公开了许多测试任务和相应的评分标准．RMFII项目在此基础之上，将部分测评任务进行改编，形成了丰富的教学资源库供教师随时查阅．与此同时，RMFII项目还与其它研究项目合作，开发了大量的数学任务在线学习平台，如与nRich项目合作的平台（https://nrich. maths.org），与Maths300项目合作的平台（http://www. maths300.com），等等．在确定了学生的统计推理学习进程之后，结合不同的统计推理任务资源，RMFII项目开发了针对不同学习进程的教学建议，给教师的教学带来了极大的方便，也在某种程度上促进了教师统计与概率教学的专业发展．

中国未来也可以逐步构建丰富的统计与概率教学资源库，这些教学资源的选取应当有扎实的理论研究作为基础，方便教师随时查阅、分享、改进，从而更好地提升教师统计与概率教学的有效性，促进其自身的专业发展．

[1] LANGRALL, CYNTHIA W, KATIEMAKAR, et al. Teaching and learning probability and statistics: An integrated perspective [M] // National Council of Teachers of Mathematics. Compendium for research in mathematics education. NY: Springer, 2017: 490–525.

[2] 童莉，张号，张宁．义务教育阶段学生数据分析观念的评价框架建构[J]．数学教育学报，2014，23（2）：45–48．

[3] 张丹．小学生数据分析观念发展过程的研究[D]．长春：东北师范大学，2015：20–21，28．

[4] WATSON J M. Assessing statistical thinking using the media [M] // GAL I, GARFIELD J. The assessment challenge in statistics education. Amsterdam: IOS Press and International Statistical Institute, 1997: 107–121.

[5] GAL I. Adults’ statistical literacy: Meanings, components, responsibilities [J]. International Statistical Review, 2002, 70 (1): 1–25.

[6] GARFIELD J, BEN-ZVI D. Developing students’ statistical reasoning: Connecting research and teaching practice [M]. NY: Springer Science & Business Media, 2008: 34, 102–105.

[7] BEN-ZVI D. Reasoning about variability in comparing distributions [J]. Statistics Education Research Journal, 2004, 3 (2): 42–63.

[8] REID J, READING C. Measuring the development of students’ consideration of variation [J]. Statistics Education Research Journal, 2008, 7 (1): 40–59.

[9] NOLL J, SHAUGHNESSY J M. Aspects of students’ reasoning about variation in empirical sampling distributions [J]. Journal for Research in Mathematics Education, 2012, 43 (5): 509–556.

[10] 史宁中，张丹，赵迪．“数据分析观念”的内涵及教学建议——数学教育热点问题系列访谈之五[J]．课程·教材·教法，2008，28（6）：40–44．

[11] SIEMON D. Developing learning progressions to support mathematical reasoning in the middle years: Introducing the reframing mathematical futures II project [C] // Melbourne Australia. 40 years on: We are still learning! Proceedings of the 40th Annual Conference of the Mathematics Education Research Group of Australasia, 2017: 651–654.

[12] WATSON J, CALLINGHAM R. Statistical literacy: A complex hierarchical construct [J]. Statistics Education Research Journal, 2003, 2 (2): 3–46.

[13] WATSON J M. Statistical literacy at school: Growth and goals [M]. New York: Routledge, 2013: 252–266.

[14] CALLINGHAM R, WATSON J, OATES G. Statistics and probability: From research to the classroom [M] // Researching and using progressions (trajectories) in mathematics education. Boston: Brill Sense, 2019: 181–204.

[15] CALLINGHAM R, WATSON J, SIEMON D. Making the connections: From statistics education research to teaching advice [C] // International Statistical Institute. Looking back, looking forward: Proceedings of the Tenth International Conference on Teaching Statistics (ICOTS10), 2018: 203.

[16] WATSON J, CALLINGHAM R. Developing learning progressions to support mathematical reasoning in the middle years: Statistical reasoning [C] // Melbourne Australia. 40 years on: We are still learning! Proceedings of the 40th Annual Conference of the Mathematics Education Research Group of Australasia, 2017: 663–666.

[17] 贺睿杰．统计调查活动的课堂实施策略——SASI框架引介[J]．外国中小学教育，2018（11）：62–70．

Introduction and Discussion on “Statistical Reasoning” in RMFII Project in Australia

GAO Xiang

(School of Teacher Education, Nanjing University of Information Science & Technology, Jiangsu Nanjing 210044, China)

“Statistics and probability” is an important mathematics learning field, and its evaluation and teaching have become a hot research issue in recent years. In order to provide reference for the research and teaching of “statistics and probability” in China, this paper introduces the relevant content of the statistical reasoning branch of Australian “Reframing Mathematical Futures II (RMFII)” project, through using methods of literature review, historical review, case studies and other methods to present the evaluation idea of “statistical reasoning”, retrospect the construction process of “statistical reasoning 8 ‘zone’ learning progression”, and combine with specific cases to analyze the learning progression in “positioning” measures for students’ statistical reasoning ability level and “linking” teaching suggestions. It brings three inspirations to the research and teaching of “statistics and probability” in China: further refine the level requirements of “data analysis literacy” and enhance operability; develop assessment tasks to explore the learning progression of statistics and probability suitable for Chinese students; and build a rich teaching resource base to improve teachers’ professional development.

statistics and probability; Australia; RMFII project; statistical reasoning; data analysis literacy

G40–059.3

A

1004–9894（2022）04–0062–06

高翔．澳大利亚RMFII项目中“统计推理”的引介与思考[J]．数学教育学报，2022，31（4）：62-67．

2022–02–06

教育部人文社会科学研究青年基金项目——数学核心素养的认知诊断测评研究（21YJC880102）；南京信息工程大学人才启动经费（2021r009）

高翔（1990—），男，江苏常州人，讲师，博士，主要从事数学课程与教学论、数学教师教育研究．

[责任编校：周学智、张楠]