中小学生数学阅读能力结构发展研究

杨红萍杨 捷杨蓉蓉

中小学生数学阅读能力结构发展研究

杨红萍1，2，杨 捷3，杨蓉蓉4

（1．山西师范大学 现代文理学院，山西 临汾 041000；2．山西师范大学 教师教育学院，山西 太原 030000；3．天津市第九中学，天津 300381；4．垣曲县中条中学，山西 运城 043700）

对小学三年级、六年级、初三、高三4个年龄切面学生的数学阅读能力结构的因素构成进行调查，结果显示：数学阅读能力结构随着年龄的增长而发生变化，一方面表现为能力结构的因素数量逐步增加，另一方面表现为比较复杂、层次较高的因素在整个结构中的相对地位不断增强．

数学阅读；能力结构；活动—因素分析法

1 问题提出

阅读是人类社会生活的一项重要活动，是人类汲取知识的主要手段和认识世界的重要途径．阅读能力是学生学习的基本能力，是其它能力的基础．《义务教育数学课程标准（2011年版）》与《普通高中数学课程标准（2017年版2020年修订）》都强调指出，应提倡阅读自学等多样化的学习方式，教师应指导学生进行阅读自学．近几年中、高考对学生的数学阅读能力也提出了更高的要求．而数学阅读能力结构不是一成不变而是随年龄变化的．研究中小学生数学阅读能力结构的发展变化，可以更好地培养学生的阅读素养，提高阅读能力．

能力结构的发展方面，不同的学者有不同的观点．加勒特（Garrett）提出分化说，认为个体的能力是逐渐分化的，儿童更多表现为一般因素的影响，而成人则有更多的群因素的影响．奥斯本和杰克森的研究结果也支持分化说．与分化说不同，陈立提出能力从合到分，再到合的主张．他指出，能力的“发展是两尖头的梭形．在初生阶段，可能是由混沌一团而逐渐分化成为各种特殊能力．长成以后则因正迁移的相互作用，能力就又由分到合了”[1]．

许多学者对阅读能力结构发展进行了研究．莫雷对小学六年级、初三年级、高三年级3个年龄切面学生的语文阅读能力结构进行分析，结果表明语文阅读能力结构随年龄的增长而发生变化，一方面表现为因素数量的增加，另一方面表现为复杂、层次高的因素在整个结构中相对地位不断增强，并进一步指出，能力结构因素增加的方式表现为“接替”模式．罗照盛和张厚粲探讨了中小学生语文阅读能力结构的组成及其发展特点，结果表明，被试的阅读理解能力[2]的水平主要受阅读理解能力结构的发展水平制约．而阅读理解能力水平的发展一般遵循量的累加与质的飞跃过程，质的飞跃意味着阅读理解能力结构的发展与分化[3]．段蕙芬等对上海3类学校（市、区重点及一般完中）初一至高三6个年级的学生进行英语阅读能力测试，并进行因素分析，结果表明各年级英语阅读能力结构因素作用不同，但有其发展规律[4]．

综上可以看出，关于阅读能力结构的发展研究，在语文、英语领域的研究较为系统、成熟，而对数学阅读能力结构的年龄特征、发展特点缺少系统的研究．研究通过“活动—因素分析法”，对小学三年级、六年级、初三年级、高三年级4个年龄切面的数学阅读能力结构的因素构成及相对地位进行分析，以揭示数学阅读能力结构的纵向发展特点．

2 研究设计

2.1 研究假设

在文献分析和已有研究的基础上，提出研究假设：数学阅读能力结构随年龄的增长而发生变化，一方面表现为因素数量的增加，另一方面表现为复杂、层次高的因素，比如元认知能力、迁移能力等，在整个结构中相对地位不断增强．

2.2 研究方法

能力结构的研究方法主要可以分为以西方为代表的因素分析法及以苏联为代表的活动分析法．因素分析法是把一组反映事物性质、状态、特点等的变量简化为少数几个能够反映出事物内在联系的、固有的、决定事物本质特征因素的统计分析方法．西方的因素分析法未能解决测验设计与结果解释的客观性问题．苏联学者提出了以活动为中心研究能力结构的活动分析法．首先对与某能力有关的活动进行分析，据此提出该能力结构模式的假设，然后按照所设想的能力结构因素设计相应的实验作业，让能力不同的被试个别完成，并对他们的完成过程进行定性分析，以检验原先所设想的能力结构因素是否符合实际，最后确定能力结构．这种方法是直觉的、经验的，难以保证能力结构的完整性及结构中因素组合的合理性．

为了克服以上两种研究方法的局限，自20世纪70年代后，对能力的研究出现了新的动向．莫雷综合了因素分析法和活动分析法的优势提出“活动—因素分析法”[5]．“活动—因素分析法”认为，能力是在个体的活动中起调节制约作用的，具体地对个体完成各种分测验的过程作定性的分析研究，便可以揭示调节这些活动的内隐心理特质．因此，可以将对各因素有高负荷的分测验的内容分别编制成相应的个别作业，让学生个别完成，然后对这个完成过程作定性分析，揭示其心理机制，从而据此对因素做出解释，称之为活动鉴别法．

2.3 研究过程

项目组采用“活动—因素分析法”（因为是系列研究，具体研究方法、研究过程及工具，请详见文[6]和文[22]，这里不再赘述），对小学三年级、六年级、初三、高三4个年龄切面的数学阅读能力结构因素已分别进行了研究．结果如下：小学三年级和六年级学生数学阅读能力结构相同，由概念理解能力、语言互译能力、阅读迁移能力、阅读推理能力、空间想象能力、信息整合能力6个因素组成[6]：初三学生包含概念理解能力、语言互译能力、阅读迁移能力、信息整合能力、阅读元认知能力、空间想象能力、阅读推理能力7个因素[7]；高三学生包含概念理解能力、抽象概括能力、阅读推理能力、语言互译能力、空间想象能力、阅读迁移能力、阅读元认知能力和信息整合能力8个因素[8]．

接下来将对4个年龄切面的数学阅读能力结构的因素构成及因素相对地位进行分析，以揭示数学阅读能力结构的纵向发展特点．

3 研究结果

4个年级的数学阅读成就测验的相关矩阵（如表1～4）．

表1 小学三年级因素间的相关矩阵[8]

注：*表示在0.05级别（双尾）相关性显著；**表示在0.01级别（双尾）相关性显著（以下同）．

表2 小学六年级因素间的相关矩阵[8]

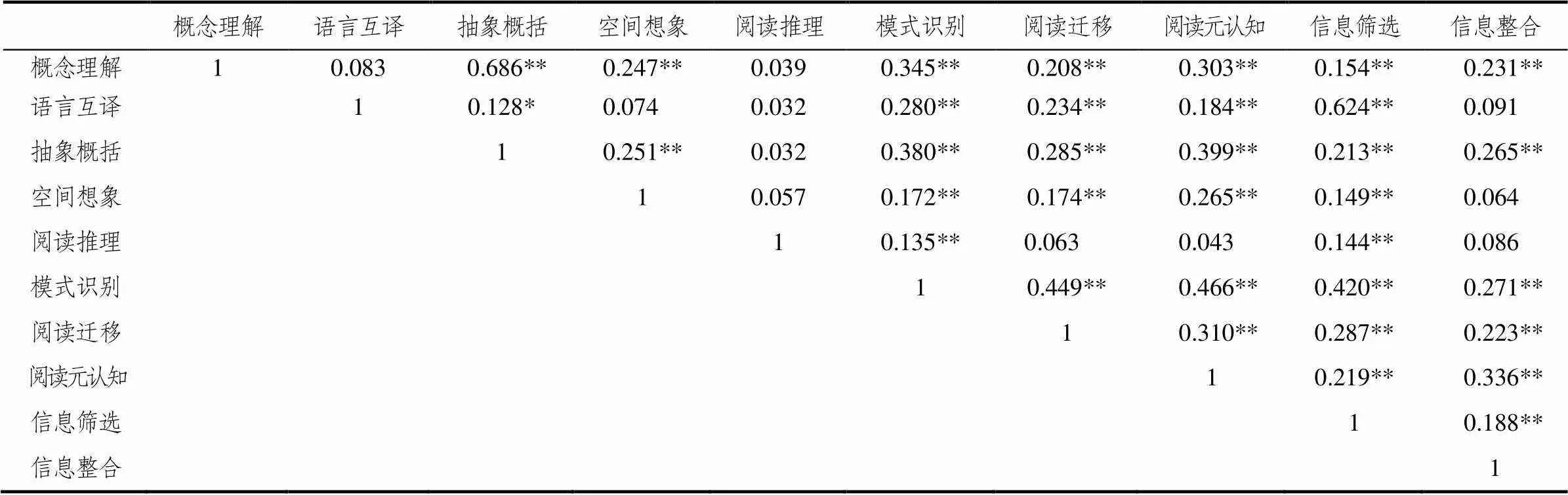
表3 初三年级因素间的相关矩阵[7]

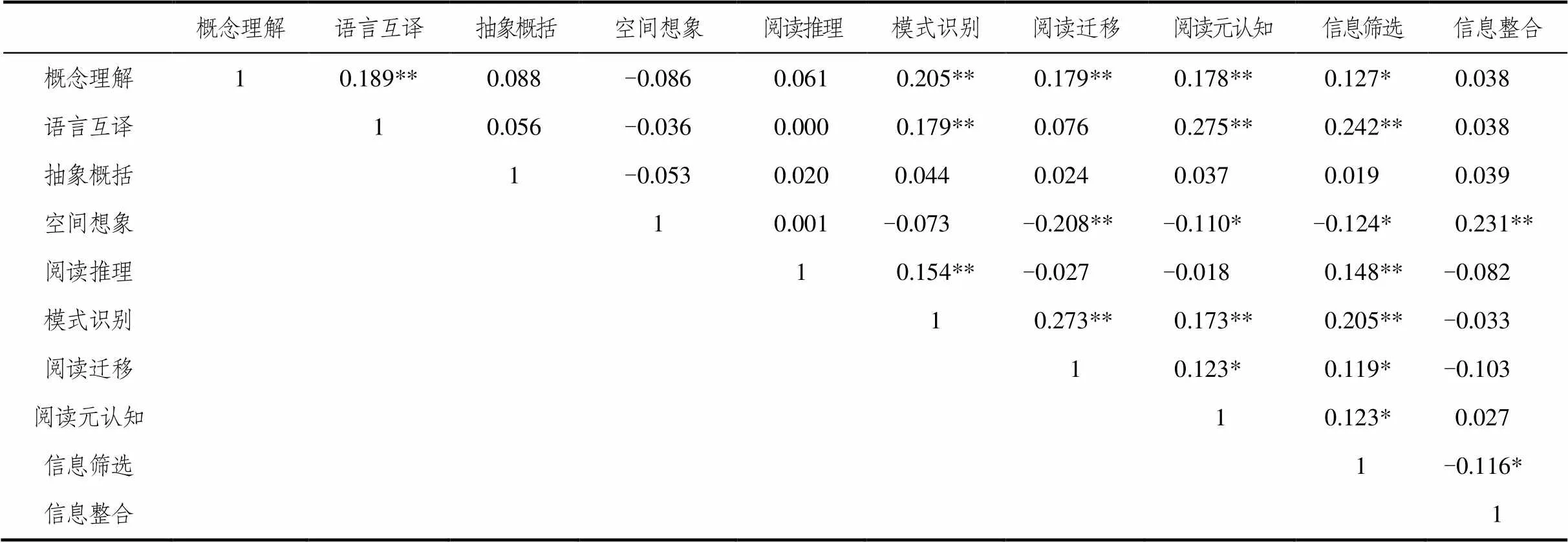
表4 高三年级因素间的相关矩阵[8]

根据4个年级数学阅读成就测验的相关矩阵，分别计算出各年级分测验的平均相关值以及达到两种显著性水平的相关系数所占的比例，结果见表5[8]．

表5 4个年级分测验间相关情况

从表5中可以看出，随着年级的升高，各分测验之间平均相关值呈下降趋势，达到各显著性水平的系数数量的总和也呈现下降趋势．可以看出，分测验间相关程度随年龄升高而逐渐减弱，阅读能力结构发展符合加勒特1946年提出的个体能力分化说．奥斯本和杰克森的研究结果也支持分化说，他们从威克斯勒儿童智力量表中选出材料编制成套测验，对6岁儿童进行追踪研究，发现入学时仅有8种因素，而一年后应用相同测验却得出10种[1]．

对4个年级的因素负荷矩阵进行整理，如表6[8]所示．

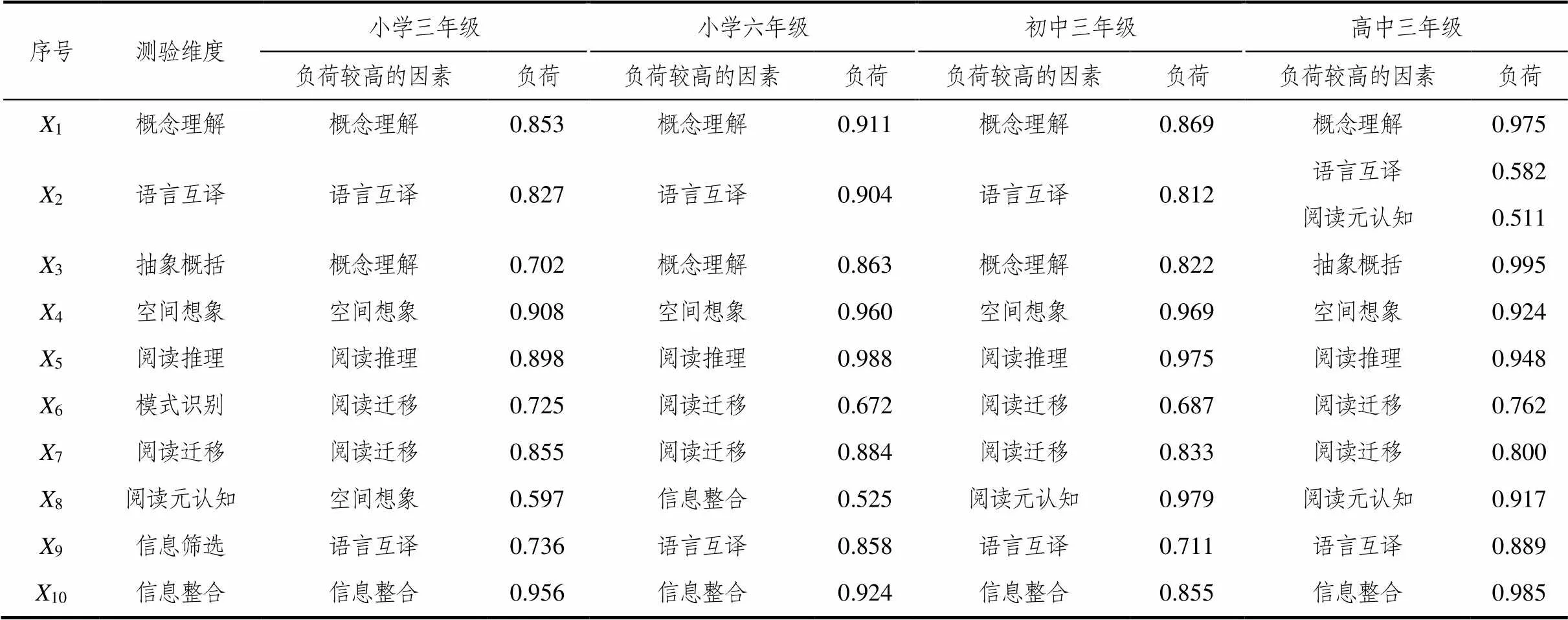
表6 4个年级数学阅读能力因素负荷

从表6中可以看出，4个年级测验卷测试维度都是10个，因素分析均按照累计贡献率大于80%确定公因素数量，得到小学三年级的6个公因素依次是信息整合（0.956）、空间想象（0.908）、阅读推理（0.898）、概念理解（0.853）、阅读迁移（0.855）、和语言互译（0.827）．六年级6个公因素依次是阅读推理（0.988）、空间想象（0.960）、信息整合（0.924）、概念理解（0.911）、语言互译（0.904）和阅读迁移（0.884）．初中三年级的7个公因素依次是阅读元认知（0.979）、阅读推理（0.975）、空间想象（0.969）、概念理解（0.869）、信息整合（0.855）、阅读迁移（0.833）和语言互译（0.812）．高中三年级的8个公因素依次是抽象概括（0.995）、信息整合（0.985）、概念理解（0.975）、阅读推理（0.948）、空间想象（0.924）、阅读元认知（0.917）、语言互译（0.889）和阅读迁移（0.800）．

从表6可以看出，不同年级学生数学阅读能力结构中的因素数量是不等的，年龄越大的学生，数学阅读能力结构的成分越多，数学阅读能力结构越来越复杂，呈现分化趋势．

各年级数学阅读能力结构的成分分化情况如表7[8]．随着理解水平的不断提高，影响被试阅读理解能力水平的因素也逐步细化，许多笼统的因素分解更加具体，更高层次的理解因素被逐步分离出来，并逐步成为影响阅读理解能力的主导因素[3]．为了得出各因素在结构中的相对地位，对4个年级各因素的方差贡献率进行归一处理，如表8[8]．

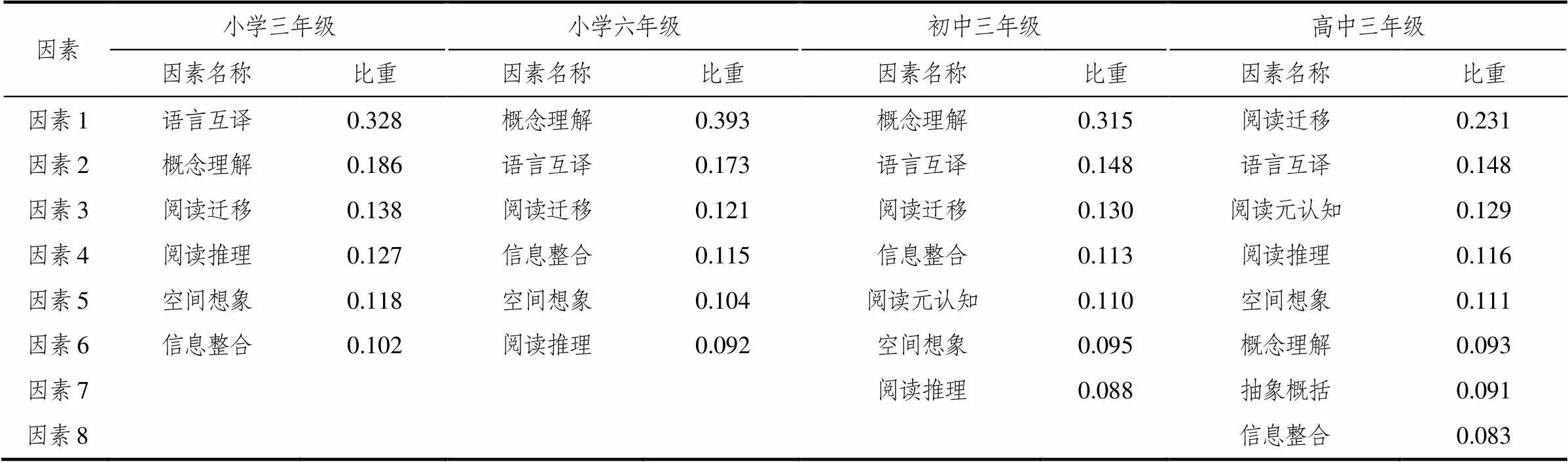
表8 4个年级各因素相对地位

从表7可以看出，不同年龄的数学阅读能力结构中各种因素的相对地位有所变化，总体趋势是更为复杂的因素，如阅读迁移、语言互译、阅读元认知等因素占据更高的地位．

阅读迁移能力在小学三年级的因素结构中占比0.138，小学六年级变为0.121，初三年级为0.130，高三年级为0.231．随着年级的升高，学生的认知结构日趋复杂，认知经验逐渐丰富．格林诺及其同事对年幼儿童的研究也表明：年幼儿童只有一种应用题图式，他们试图以其仅有的图式来解决所有应用题，相对而言，年长的学生建立了针对不同问题类型的不同图式[9]．张阔、阴国恩和王敬欣研究显示，在成人的类别学习过程中，已有的知识发挥着重要作用[10]．随着学生获取知识的方式趋于自主独立，阅读作为获得知识的必要手段，也使得阅读迁移能力在数学阅读能力结构中越来越重要．

语言互译能力在小学三年级占比最高，小学六年级、初三、高三年级所占比重逐渐稳定，高于大部分因素．邵光华认为数学阅读过程同一般阅读过程一样，包括语言符号（文字、符号、图表等）的感知和认读、新概念的同化和顺应、阅读材料的理解和记忆等各种心理活动因素[11]．杨红萍研究指出，语言转译是数学阅读的核心要素，主要指数学语言（文字语言、符号语言和图表语言）之间的互译、转换[12]．数学语言与其它学科语言最大的不同之处在于语言形式的丰富性，且需要将不同语言进行相互转换达到理解的目的．因此在数学学习的早期阶段对于语言互译能力要求较高，随着年级的增长，对于其它较为高级的能力有更高要求．

阅读元认知能力在初三阶段新分化出来，在高三比重有所提升．研究表明，与年长阅读者相比，年幼阅读者不太容易监控他们的活动过程，也不太会随不同的任务而改变其阅读策略[13-14]．秦娟对1 349名初中生进行自主学习能力测试，利用探索性因素分析，结果发现，初三年级显著优于初一、初二年级，初二较初一无明显增长，初一与初二之间不存在显著性差异[15]．

4 研究结果分析

4.1 能力结构总体发展情况分析

从统计结果看，其一，不同年级学生数学阅读能力结构中的因素数量是不等的，年龄越大的学生，数学阅读能力结构的成分越多，数学阅读能力结构越复杂，呈现分化趋势．其二，不同年龄的数学阅读能力结构中各种因素的相对地位有所变化，总体趋势是更为复杂、高级的因素占据更高的地位．

可以看出，数学阅读能力结构因素数量增加的原因在于，原来由一个因素解释的多个测验维度，后来需要两个或者更多因素来解释．表现在因素数量上就是由原来一个公因素变成两个公因素．小学三年级和六年级数学阅读能力结构有6个相同的公因素：概念理解、语言互译、空间想象、阅读推理、阅读迁移和信息整合．这些因素在初三和高三的公因素中依然存在，但是随着年龄增长，初三学生数学阅读能力结构从信息整合中分化出了阅读元认知，具有7个公因素．高三学生数学阅读能力结构在初三的基础上，由概念理解分化出了抽象概括，具有8个公因素．从以上分析可以看出，随年龄增长，从原来公因素的某些因素中分化出新的因素，形成了因素随年龄增加的趋势．

4.2 不同因素的具体发展情况分析

信息整合能力是指对阅读材料所反映的信息优化组合、进行综合分析的能力，任何学段都是文本解读的基本能力，在4个年级阅读能力结构中的地位相对较为稳定．

概念理解能力在小学三年级、六年级、初三的数学阅读能力结构中都占据了很高的比重，在高三年级的结构中比重有所降低．概念学习是数学学习的基础，在小学和初中阶段是学生抽象思维逐步发展的关键阶段．在高中阶段，学生的抽象思维能力比较成熟，概念理解能力逐步增强，完成概念理解所需的认知负荷下降．

阅读推理能力在4个年级的能力结构中的地位相对较为稳定．皮亚杰将儿童推理的发展过程分为3个阶段：前运算阶段（2～8岁）、具体运算阶段（7～12岁）、形式运算阶段（11～12岁）．处于具体运算阶段的儿童越来越意识到存在与各分离事件中的关系，处于形式运算阶段的儿童可以脱离现实的物质世界，不再一味相信与物质世界相接触的运动和实验，而是采用一个法则或假设，将它应用到紧密相连的推理步骤的长链中去[16]．王小宁研究表明：推理能力随着年龄的增长不断发展，其中演绎推理在小学五年级开始形成，初一年级开始占优势，在高中二年级已趋成熟[17]．

语言互译能力在4个年级的数学阅读能力结构中，都占有很重要的地位，在结构中的比重超过大部分因素，但是随着年龄的增长，初三和高三学生数学阅读能力结构中，语言互译能力在整个结构中的比重降低了．

阅读迁移能力随着年龄的增长，在数学阅读能力结构中保持重要的地位，在高三年级的结构中成为最重要的因素．喻平曾指出，阅读的第二阶段是理解，其间，读者要激活与当前信息相关的个体认知结构中的有关观念进行迁移，才能达成与新信息的联系，实现对材料的理解[18]．

空间想象能力变化不大，相对于初三年级，在高三结构中地位有所上升．皮亚杰的研究表明，儿童在八、九岁时，才会画出体现透视、比例与距离的图画．在形式运算水平，儿童的思维变成了假设与演绎的思维，思维本身已经摆脱了感觉经验或知觉的具体水平．该阶段的儿童才能理解具有无限性和无穷性的连续性几何概念[16]．

阅读元认知能力在初三阶段新分化出来，其在高三学生的数学阅读能力结构中的比重有所提升．中学生数学学习自我监控能力的发展符合从他控到自控、从不自觉经自觉到自动化、敏感性逐渐增强、迁移性逐渐提高、从局部到整体等基本规律[19]．在初一至高一期间，青少年学习自我监控能力的发展速度比小学生大很多，且计划性、准备性、方法性和反馈性得到了较好的发展[20]．

抽象概括能力在高三阶段新分化出来．王宪鈿指出，在少年期及青年期抽象思维出现幻想性，13岁时有显著发展，在13岁之前抽象概念在儿童的思维中还是不稳定的．在描写目的和客观要求方面较宽广的综合性则在14～17岁时才出现[21]．

综合以上分析，可以看出，随着年龄的增长，阅读迁移、阅读元认知、阅读推理这类对阅读材料精细加工的能力成分逐渐占据了主要地位，分量越来越大，逐渐成为影响学生数学阅读能力的主要原因．而概念理解、语言互译这类基础的能力成分相对地位略有降低．数学阅读能力结构中成分相对地位的变化反映出数学阅读能力结构的发展特点：随年龄的增长，更为复杂、高级的因素在数学阅读能力结构中占据更重要的地位[23-44]．

5 研究结论

研究表明，三年级和六年级学生数学阅读能力结构相同，由概念理解能力、语言互译能力、阅读迁移能力、阅读推理能力、空间想象能力和信息整合能力6个因素组成；初三学生包含概念理解能力、语言互译能力、阅读迁移能力、信息整合能力、阅读元认知能力、空间想象能力和阅读推理能力7个因素；高三学生包含概念理解能力、抽象概括能力、阅读推理能力、语言互译能力、空间想象能力、阅读迁移能力、阅读元认知能力和信息整合能力8个因素．数学阅读能力结构随着年龄的增长而发生变化，一方面表现为能力结构的因素数量逐步增加，另一方面表现为比较复杂、层次较高的因素在整个结构中的相对地位不断增强．

[1] 李孝忠．能力心理学[M]．西安：陕西人民教育出版社，1987：158．

[2] 莫雷．中小学生语文阅读能力结构的发展特点[J]．心理学报，1992（4）：346-354．

[3] 罗照盛，张厚粲．中小学生语文阅读理解能力结构及其发展特点研究[J]．心理科学，2001（6）：654-656，764．

[4] 段蕙芬，蒋子诚，梅卫国．中学生英语阅读能力结构及其发展初探[J]．心理科学，2000（5）：547-551，637．

[5] 莫雷．能力结构研究的基本方法与方法论问题[J]．心理学报，1988（3）：305-311．

[6] 杨红萍，杨捷．小学生数学阅读能力结构的因素分析[J]．数学教育学报，2019，28（5）：14-18．

[7] 杨蓉蓉．初中生数学阅读能力结构因素分析[D]．临汾：山西师范大学，2018：13-36．

[8] 杨捷．中小学生数学阅读能力结构发展研究[D]．临汾：山西师范大学，2019：91-122．

[9] Riley M S, Greeno J M, Heller J I. Development of children’s problem-solving ability in arithmetic [M]. Orlando, FL: Academic Press, 1984: 153-196.

[10] 张阔，阴国恩，王敬欣．儿童类别学习中知识效应的年龄差异[J]．心理发展与教育，2005（2）：75-80．

[11] 邵光华．数学课堂阅读指导策略[J]．课程·教材·教法，1998，10（8）：23-25．

[12] 杨红萍．数学语言对数学阅读的影响研究[J]．数学通报，2010，38（9）：19-23．

[13] MARKMAN E. Realizing that you don’t understand: Elementary school children’s awareness of inconsistencies [J]. Child Development, 1979 (50): 643-655.

[14] MYERS M, PARIS S B. Children’s metacognitive knowledge about reading [J]. Journal of Educational Psychology, 1978 (70): 680-690.

[15] 秦娟．初中生自主学习能力结构及发展特点研究[D]．桂林：广西师范大学，2006：52．

[16] 科普兰R W．儿童怎样学习数学——皮亚杰研究的教育含义[M]．上海：上海教育出版社，1985：257-266．

[17] 王小宁．小学生数学推理能力发展的研究[D]．南京：南京师范大学，2013：9．

[18] 喻平．数学教学心理学[M]．北京：北京师范大学出版社，2009：209．

[19] 章建跃，林崇德．中学生数学学科自我监控能力的发展[J]．中国教育学刊，2000（4）：46-49．

[20] 沃建中，林崇德．青少年自我监控能力的发展研究[J]．心理科学，2000（1）：10-15，124．

[21] 王宪鈿．国外有关儿童思維发展的一些研究[J]．心理科学通讯，1964（2）：35-40．

[22] 杨红萍，肖志娟．问题表征对数学阅读能力的影响研究[J]．数学教育学报，2019，28（2）：70-74．

[23] 杨红萍，喻平．个体CPFS结构与阅读自我监控对数学阅读的影响[J]．数学教育学报，2011，20（5）：59-61，69．

[24] 杨红萍．国内外数学阅读研究概览[J]．数学教育学报，2013，22（5）：14-17．

[25] 杨红萍．数学阅读教学叙事研究[J]．数学教育学报，2014，23（5）：27-32．

[26] 郑毓信．数学思维教学的“两阶段理论”[J]．数学教育学报，2022，31（1）：1-6．

[27] 王嵘．数学文化融入中学教科书的内容与方法[J]．数学教育学报，2022，31（1）：19-23．

[28] 王海青，曹广福．问题驱动数学教学的基本原则与思想及其实施步骤[J]．数学教育学报，2022，31（1）：24-27．

[29] 李杨，黄碧娟，李红霞，等．初一学生数学学习动机和坚持性：数学—性别刻板印象的影响[J]．数学教育学报，2022，31（1）：35-41．

[30] 孙思雨，许添舒，孔企平．基于潜在类别分析的小学生早期代数思维水平研究[J]．数学教育学报，2022，31（1）：52-58．

[31] 唐佳丽，李勇．“统计与概率”在小学数学教材中的编排分析[J]．数学教育学报，2022，31（1）：59-63．

[32] 李沐慧，徐斌艳．中国数学问题提出能力培养的发展路径与启示[J]．数学教育学报，2022，31（1）：91-96．

[33] 李昌官．数学发现与发明关系新说[J]．数学教育学报，2022，31（1）：97-102．

[34] 范文贵，李燕．小学生解决万以内退位减法错误类型及影响研究[J]．数学教育学报，2021，30（6）：32–38．

[35] 黄晓林，黄秦安．中国三十年来小学阶段分数研究文献的系统分析及启示[J]．数学教育学报，2021，30（6）：39–45．

[36] 邹学红，周钧．基于问题理解的学生问题解决错误“诊断”研究[J]．数学教育学报，2021，30（6）：46–51．

[37] 林胜威．数感的修订变化与内涵认识[J]．数学教育学报，2021，30（6）：69–73．

[38] 张侨平，邢佳立，金轩竹．小学数学教学中数学推理的理论和实践[J]．数学教育学报，2021，30（5）：1–7．

[39] 刘久成．新中国成立以来小学数学“长度单位”教材内容的演进与思考[J]．数学教育学报，2021，30（5）：8–13．

[40] 巩子坤，杨婷，张都，等．三～六年级学生分数概念的错误理解及其发展[J]．数学教育学报，2021，30（5）：14–20．

[41] 章飞，俞梦飞，顾继玲．初中数学教科书中概念的呈现方式及一致性研究[J]．数学教育学报，2021，30（5）：21–27．

[42] 于文华，王光耀，蔡金法．基于BEA的个体问题解决干预有效性研究[J]．数学教育学报，2021，30（5）：28–32．

[43] 王海青，曹广福．从《原本》谈中学平面几何课题式教学研究[J]．数学教育学报，2021，30（5）：39–46．

[44] 孙虎，张伟平，陈志辉，等．基于核心素养的六年级学生数感现状调查研究[J]．数学教育学报，2021，30（4）：41-47．

A Study on the Structure Development of Mathematical Reading Ability of Primary and Middle School Students

YANG Hong-ping1, 2, YANG Jie3, YANG Rong-rong4

(1. College of modern arts and Sciences, Shanxi Normal University, Shanxi Linfen 041000, China;2. Teachers Education School, Shanxi Normal University, Shanxi Taiyuan 030000, China;3. NO.9 High School Tianjin, Tianjin 300381, China; 4. Yuanqu Zhongtiao Middle School, Shanxi Yuncheng 043700, China)

This paper analyzes the factor structure of Mathematics Reading ability of students in 3th grade, 6th grade, 9th grade and 12th grade, and presents their factor structure developmental characteristics. Participants of each grade are recruited from three schools. They are composed of 381 students in 3th grade, 395 in 6th grade, 364 in 9th grade and 359 in 12th grade in this study. The results show that the factor structure of Mathematics Reading ability changes with age. The number of factors manifested as Mathematics Reading ability structure increases gradually while more complex and higher-level factors play more and more important roles in the whole structure.

mathematical reading; ability structure; activity-factor analysis

G40–03

A

1004–9894（2022）04–0080–06

杨红萍，杨捷，杨蓉蓉．中小学生数学阅读能力结构发展研究[J]．数学教育学报，2022，31（4）：80-85．

2022–04–09

山西省哲学社会科学规划课题——山西省中小学学科育人路径研究（2020YJ063）；山西省研究生教育改革课题——基于智慧平台的学科教学专业研究生《中学数学教学设计》课程建设（2020YJJG154）；山西省教育科学“十四五”规划项目——中小学生全阅读素养培育现状研究（GH-21042）；山西师范大学现代文理学院基金项目——数学阅读影响因素的路径分析（2019JCYJ11）

杨红萍（1969—），女，山西稷山人，教授，博士，硕士生导师，主要从事数学课程与教学论研究．

[责任编校：陈隽、陈汉君]