基于猎人猎物优化算法求解TSP问题
王 芬,杨 媛
(宁夏师范学院 数学与计算机科学学院,宁夏 固原 756099)
旅行商问题(Traveling Salesman Problem,TSP)是工程、离散数学、计算和运筹学等领域中重要的研究课题之一[1].近年来有很多群体智能算法被用于解决TSP问题.TSP问题不难理解,但很难解决,这一问题自提出以来,就引起了许多研究人员的兴趣,但是一直没有找到有效地解决办法.解决这一问题有两类方法,一类是传统的方法,一类是智能优化算法.传统的TSP求解算法结果并不理想,所以学者们试图用群体智能算法来解决这一NP难问题.粒子群算法(PSO),麻雀优化算法(SSA)等都是群体智能算法,是模拟鸟群或麻雀等觅食行为产生的算法.虽然这些算法不能在有限的时间内得到最优解,但可以在一定时间范围内得到比较满意的解.目前,大多使用启发式算法解决这类NP难问题,例如遗传算法[2]、麻雀优化算法[3]和粒子群算法[4]等.猎人猎物优化算法是2022年提出的一种新型智能优化算法,该算法通过模拟动物猎食的过程对问题进行寻优,具有收敛速度快,寻优能力强的特点.故本文用该算法求解TSP问题.
1 旅行商问题
旅行商问题被定义为一个推销员在所有城市的旅行,以最低的成本回到最初的城市.TSP问题的计算规模随着城市节点的增多呈指数增大,能否以合理的成本找到理想解决方案是非常重要的.该问题由一组N个城市节点组成,任意两个城市节点之间的间距已知.推销员从一个节点开始,每个节点经过且经过一次(起始节点除外)使总移动距离最小的方式返回到起始节点.
TSP问题可以用图形G=(V,E) 表示,其中 V={1,2,…,N}是城市节点的集合,E 是边的集合.每个边都有一个表示距离的值,该距离表示与其关联的各城市之间的距离.推销员旅行到N个城市(或节点)时,他只去每个城市一次,并以最短的旅行距离结束.令dji为第j个城市与第i个城市之间的距离.TSP问题可以化为如下模型
xjk,∀j,k∈V&j≠k,
(1)
(2)
(3)
(4)
如果推销员从城市j到城市i,则xji=1,否则xji=0.
上述模型可以简化为确定一个城市序列(x1,x2,…,xN,x1),该序列使(5)式最小的.
(5)
2 猎人猎物优化算法原理
猎人猎物优化算法[5](Hunter-prey optimizer,HPO)是2022年提出的一种新的基于种群的优化算法.该算法模拟豹子、狮子等食肉动物捕食鹿和羚羊等猎物的行为而产生的.
2.1 初始化
猎食者种群由(6)式随机初始化位置.
xi=rand(1,d)*(u-l)+l,
(6)
其中,xi是猎食的位置,l是最小值(下界),u是最大值(上界),d是问题变量的数量(维度).
2.2 猎食者搜索
公式(7)是猎食者的搜索机制.
xi,j(t+1)=xi,j(t)+0.5[(2CZPpos(j)-xi,j(t))+(2(1-C)Zγ(j)-xi,j(t))],
(7)
其中,xi,j(t)是猎食者当前位置,xi,j(t+1)是猎食者下一次的位置,Ppos是猎物的位置,γ是所有位置的平均值,Z是自适应参数,由公式(9)计算得
P=R1 (8) Z=R2⊗IDX+R3⊗(~IDX), (9) 其中,R1和R3是[0,1]内的随机向量,P是R1 (10) 其中,i是当前迭代次数,M是最大迭代次数. 公式(7)中的γ为 (11) 计算欧几里得距离为 (12) 根据狩猎场景,当猎食者捕获猎物时,猎物会死亡,下一次,猎食者会移动到新的猎物位置.为了解决这个问题,考虑一种递减机制,如(13)式所示. k=round(C×N), (13) 其中,N是搜索种群的数量.在算法开始时,k的值等于N.最后一个距离搜索个体的平均位置γ最远的搜索个体被选择为猎物,并被猎食者捕获.假设最佳安全位置是全局最佳位置,因为这将使猎物有更好的生存机会,猎食者可能会选择另一个猎物.(14)式用于更新猎物位置. xi,j(t+1)=Tpos(j)+CZcos(2πR4)×[Tpos(j)-xi,j(t)], (14) 其中,xi,j(t)是猎物的当前位置,xi,j(t+1)是猎物的下一次迭代位置,Tpos(j)是全局最优位置,Z是由式(9)计算的自适应参数,R4是[ 0, 1 ]内的随机数,C是探索和开发之间的平衡参数,其值在算法的迭代过程中减小,并由式(10)计算,cos函数及其输入参数允许下一个猎物位置在不同半径和角度的全局最优位置.为了选择猎食者和猎物,结合式(7)和(14)提出了下式. xi(t+1)=xi(t)+0.5[(2CZPpos(j)-xi(t))+(2(1-C)Zγ(j)-xi(t))], (15) xi(t+1)=Tpos+CZcos(2πR4)×(Tpos-xi(t)), (16) 其中,R4是[ 0, 1 ] 范围内的随机数,β是一个调节参数,本文设置为0.1.如果R5<β,搜索种群将被视为猎人,搜索下一个位置将用式(15)更新;否则,搜索种群将被视为猎物,搜索下一个位置将用式(16)更新. 算法具体步骤如下. 步骤1 初始化种群; 步骤2 设置算法相关参数; 步骤3 计算适应度值,并记录最优位置; 步骤4 根据公式(9)和公式(10)更新C和N; 步骤5 根据R4的值更新位置; 步骤6 计算适应度值; 步骤7 判断是否满足停止条件,如果满足则输出最优解,否则转向步骤4. 算法流程图如图1所示. 图1 算法流程图 实验用MATLAB进行编程.为验证提出算法的有效性,用本文提出的猎食者算法与麻雀搜索算法、粒子群算法进行仿真对比实验.实验分两组,第一组实验中城市的坐标由随机产生,城市个数为20.第二组实验采用TSPLIB中的 att48、eil51和rat99的 TSP 数据对猎食者算法与麻雀搜索算法、粒子群算法结果进行对比.设置的初始参数为种群个数为 100,最大迭代次为2000. 随机产生的20个城市的坐标如图2所示.三种算法的收敛曲线图如图3所示. 图2 随机产生的城市坐标 图3 各算法适应度曲线 由图2可以看出,在求解TSP问题时, HPO算法与SSA算法和PSO算法相比时间更短,收敛速度更快. 三种算法的路径规划图如图4所示. 图4 三种算法路径规划图 从图4可以直观地看出,HPO算法的路径规划比SSA算法和PSO算法更合理. 采用TSPLIB中的att48、eil51和rat99的TSP数据进行实验,各算法30次独立实验的最优值、平均值、迭代次数如表1所示. 表1 三种算法的比较 从表1的实验结果可以看出,HPO算法在求解TSP 问题时,与SSA算法和PSO算法相比,得到的最优解相对更好.体现出HPO算法具有收敛速度快,寻优能力强的特点,且在求解TSP问题时具有一定的优越性. 旅行商问题是经典的组合优化 NP 问题,有重要的现实研究意义.文章对猎食者算法的原理,更新策略,算法流程进行分析,并将他应用到解决TSP问题中.通过对比实验验证该算法的全局搜索能力与收敛性,结果表明该算法的性能优于其他算法,验证了猎食者算法有效性.
3 实验仿真及分析
3.1 初始数据随机产生
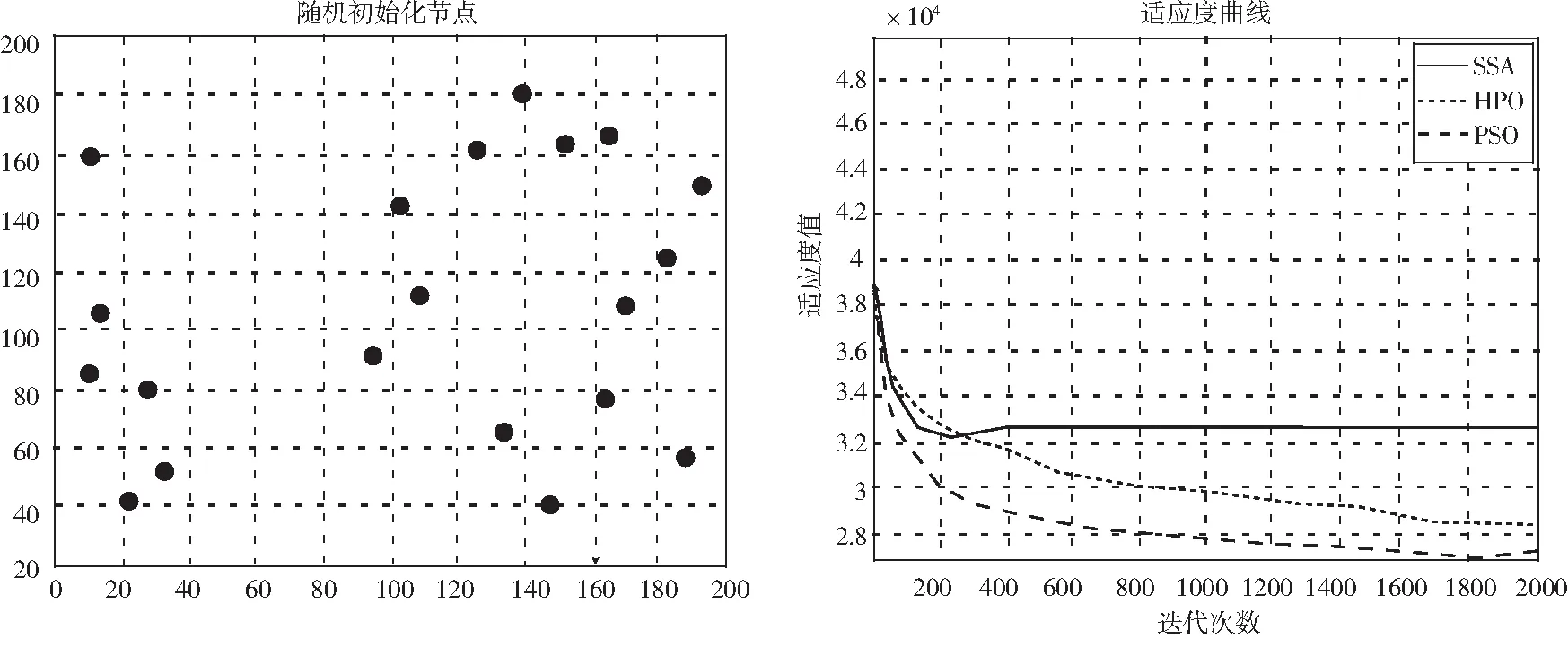
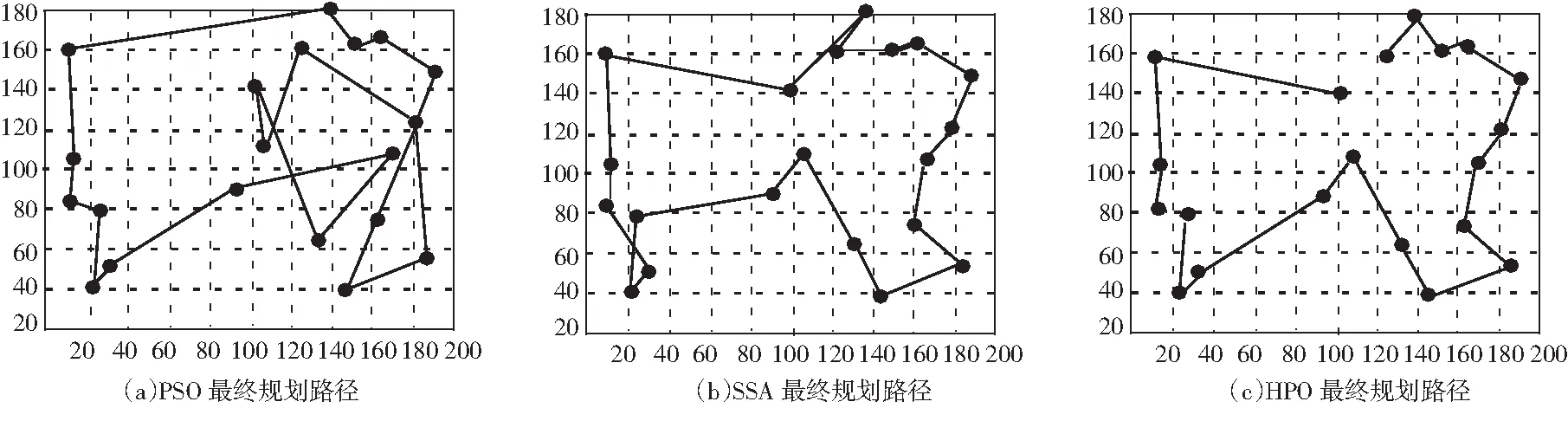
3.2 TSPLIB数据
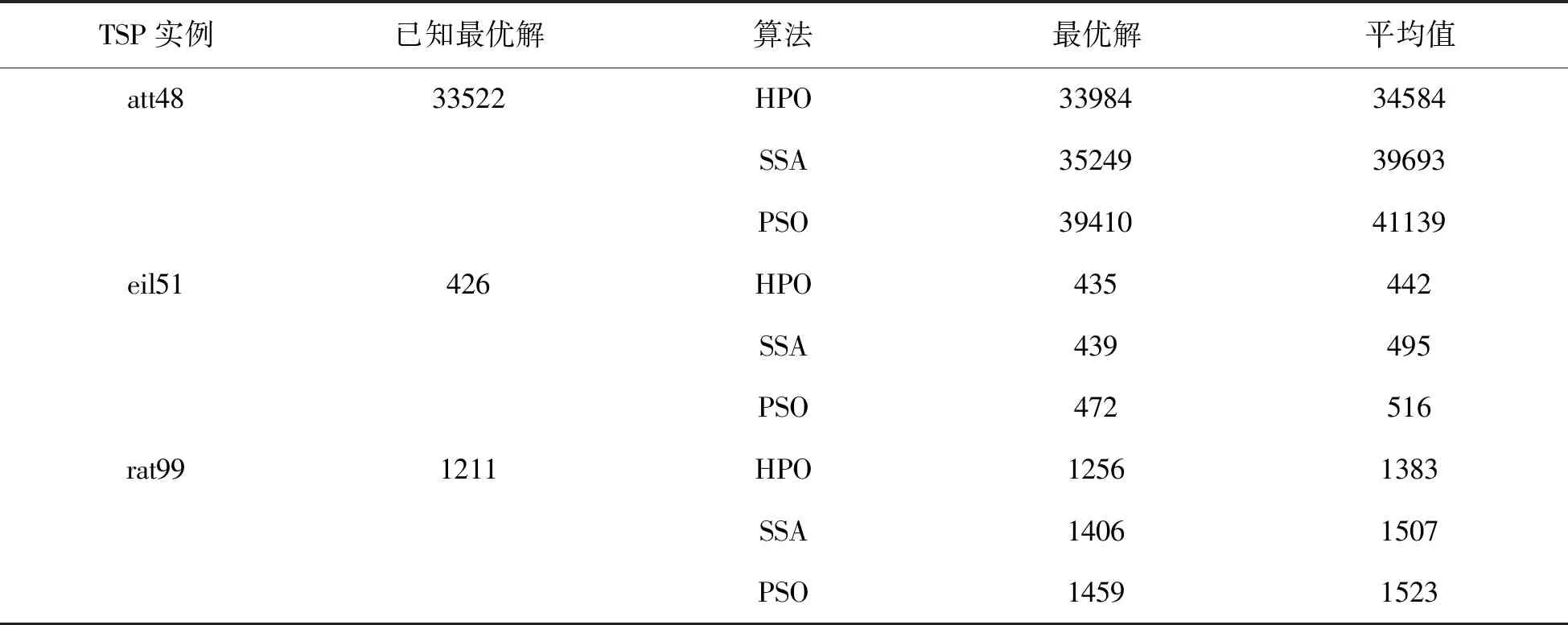
4 结论

