海豚捕食沙丁鱼群的运动行为模型

闫 洁，韩惠丽，2，周春梅

(1.宁夏师范学院 数学与计算机科学学院，宁夏 固原 756099；2.宁夏大学 数学统计学院，宁夏 银川 750021)

在海洋中，很多生物因生存、觅食、避险或繁殖等原因集群运动[1]，存在丰富的食物链和食物网，通过层层捕食，来维持海洋生态圈的稳定.海豚与沙丁鱼之间也存在非常精彩的博弈，数百万的沙丁鱼以聚成大群的方式来对抗海豚的捕食，在没有外部威胁或障碍物时，沙丁鱼群聚成接近球形的形态，是典型的自组织复杂运动[2]过程，个体间通过某种规则聚集在一起，当海豚接近并冲进沙丁鱼群时，鱼群躲避并继续聚成一团.使沙丁鱼群体表现出协调性和智能性[3]，大大降低被捕食的概率.同时海豚会配合行动，以提高捕食沙丁鱼的效率.本文模拟将海豚捕食沙丁鱼群的运动行为模型分为海豚回声定位模型、未接近沙丁鱼群的海豚运动模型、无领导者的沙丁鱼群惯性运动模型、有领导者的沙丁鱼群非惯性运动模型、沙丁鱼集群运动模型、海豚捕食沙丁鱼群模型和沙丁鱼逃逸模型.

1 海豚回声定位模型

由于水下光线很暗，海豚通过回声定位来判断鱼群的整体位置，如图1所示，海豚在觅食的时候产生回声定位信号，信号具有短脉冲、高强度和高指向性，用来探测目标的距离、方位和体积.依靠发射和接收回声定位信号的时间差估计目标的距离方位,通常有三种方式，有指向性的发射和有指向性的接收，有指向性的发射和无指向性的接收，无指向性的发射和有向性的接收.

图1 海豚回声定位原理图

如图2所示，在中远场时，假设声波以平面波方式传播[4]，根据二元测向原理，目标方位可由下式近似估计

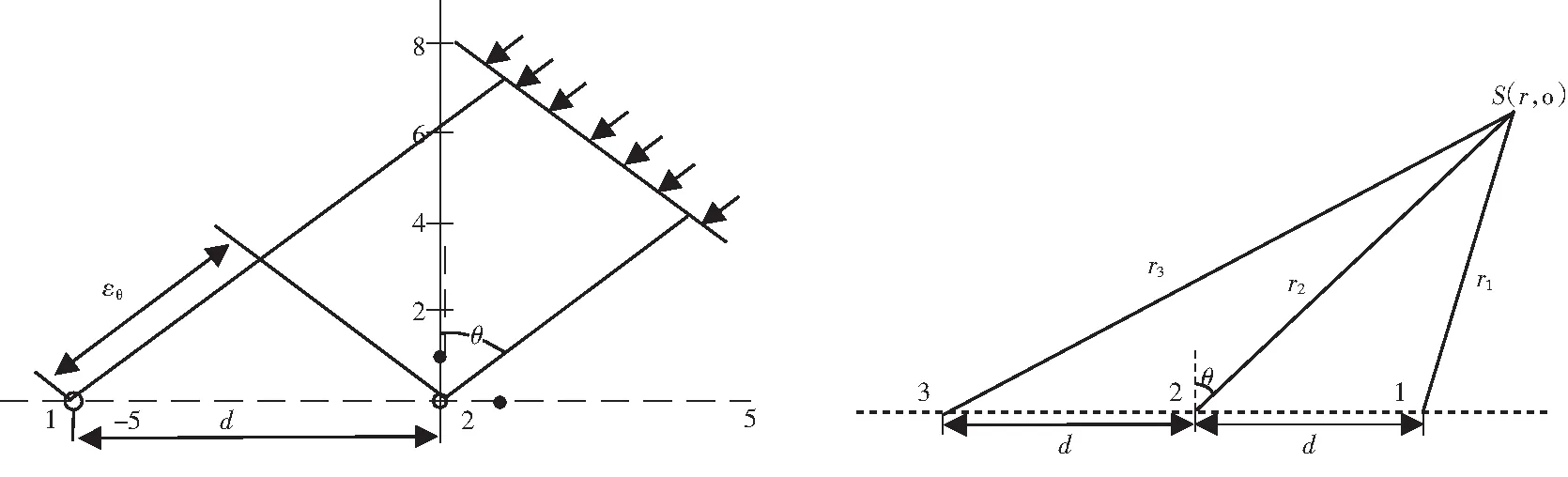
图2 远场时的二元测向模型 图3三元定位模型

如图3所示，在近场时，假设目标是点源，则声波按球面波方式传播[3]，假设1，2，3分别为三个子阵的声中心，目标方位角θ是线阵声中心处法线与r2的夹角，c为声速，r1，r2，r3为目标到线阵中心的距离，目标的声信号到达各个阵元的时延差

根据以上的三个等式可推导出目标方位的精确表达式

因此可以发现，在距离较远时，根据二元侧向模型，海豚的回声定位只能判断大体积鱼群的位置，对个体单位的定位效果较差.在距离较近时，根据三元定位模型，海豚的回声定位能精确到定位到个体.

2 未接近沙丁鱼群的海豚运动模型

对于单个海豚，将其质点化，海豚的位置可表示为

pB(t)=[xB(t),yB(t),zB(t)].

海豚的速度为vB(t),则海豚的状态为

ΩB={[pB(t),vB(t)]}.

海豚利用声波定位十几公里外的鱼群，在接近鱼群时海豚本身的感知域可视为覆盖全鱼群.海豚的定位系统[5]能判断整个沙丁鱼群，但是难以分辨每个沙丁鱼个体.因此，海豚的运动速度可表示为

海豚的实际运动能力

vBmin≤vB(t)≤vBmax,∀t.

因此,海豚的位置可表示为

(1)

海豚确定目标肩并肩前行，可将 (1) 式看作二维平面的函数，多只海豚是以 (1) 式为平面，向z轴延伸的一柱面图形上运动.

3 无领导者的沙丁鱼群惯性运动模型

如图4所示，无领导者沙丁鱼集群行为的影响作用分为内部作用和外部作用，沙丁鱼集群运动中，所有个体向同一方向运动是重要的集体规则状态特征，即为群体的一致性原则[6].沙丁鱼集群运动按照距离的不同，群体内部作用分为吸引和排斥.

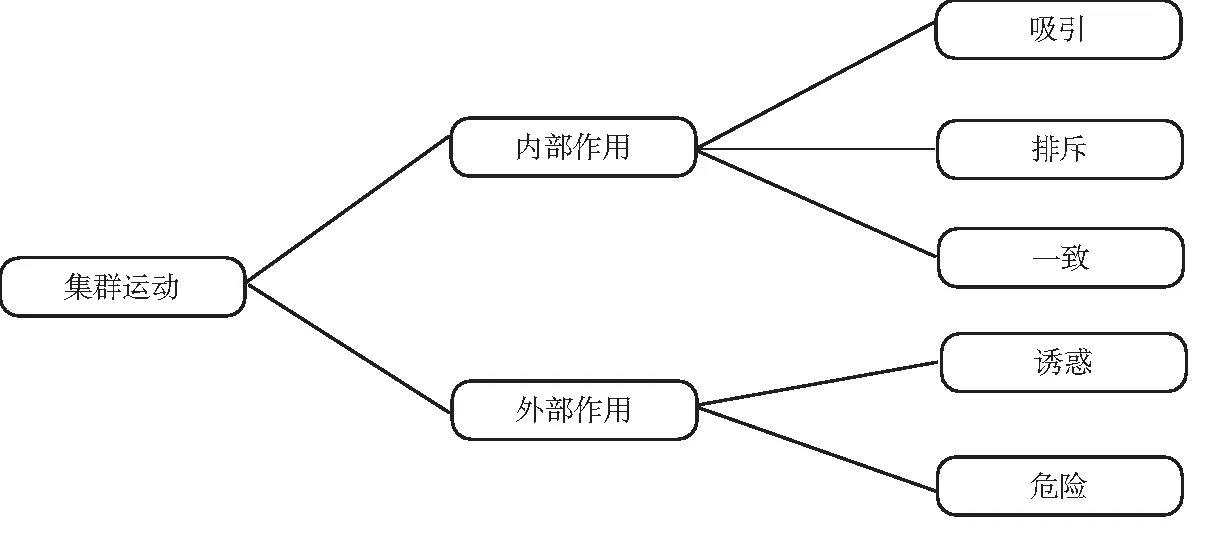
图4 无领导者沙丁鱼集群运动的作用

沙丁鱼集群运动中，对于外界有益或有害于群体的事物，造成群体趋向或背向于事物运动的趋势分为诱惑和危险.

作用力可以改变物体的运动状态，因此假设对群体的各种影响抽象为作用力，将内部作用的影响分为吸引力、排斥力和一致力，将外部作用分为诱惑力和危险力.

惯性运动指沙丁鱼群体中任意个体在某一时刻的速度V(k)受各种作用产生的加速度A(k)和上一时刻的速度V(k-1)共同影响，矢量表达式为V(k)=V(k-1)+A(k).个体的空间位置为X(k)，运动速度为V(k)，加速度为A(k).

个体由排斥力产生的加速度Ar(k)为

其中，Rand()为0～1之间平均分布的随机数，提高算法的鲁棒性[4].

个体由吸引力产生的加速度Aa(k)为

个体由一致力产生的加速度Ao(k)为

诱惑源的位置为Xt，被诱惑产生的加速度At(k)为

At(k)=Rand()·(Xt-Xi).

危险源的位置为Xf，被危险产生的加速度Af(k)为

Af(k)=-Rand()·(Xf-Xi).

因此，总加速度A(k)为

A(k)=Aa(k)+Ar(k)+Ao(k)+At(k)+Af(k).

设吸引力、排斥力、一致力、诱惑力和危险力的作用对个体的权重因子分别为ωa,ωr,ωo,ωt和ωf，则总加速度A(k)改写为

A(k)=ωaAa(k)+ωrAr(k)+ωoAo(k)+ωtAt(k)+ωfAf(k),

其中ωa,ωr,ωo,ωt,ωf∈[0,1],且ωa+ωr+ωo+ωt+ωf=1.

因此，个体的速度计算为

V(k)=V(k-1)+A(k).

个体的位置由初始位置和速度共同确定

X(k+1)=X(k)+V(k).

当ωa=0.2,ωr=0.2,ωo=0.1,ωt=0.5,ωf=0,诱惑源为(80,80)，恐惧源为(20,20)时，如图5所示，利用平面直角坐标系描述无领导者的沙丁鱼惯性运动情况.

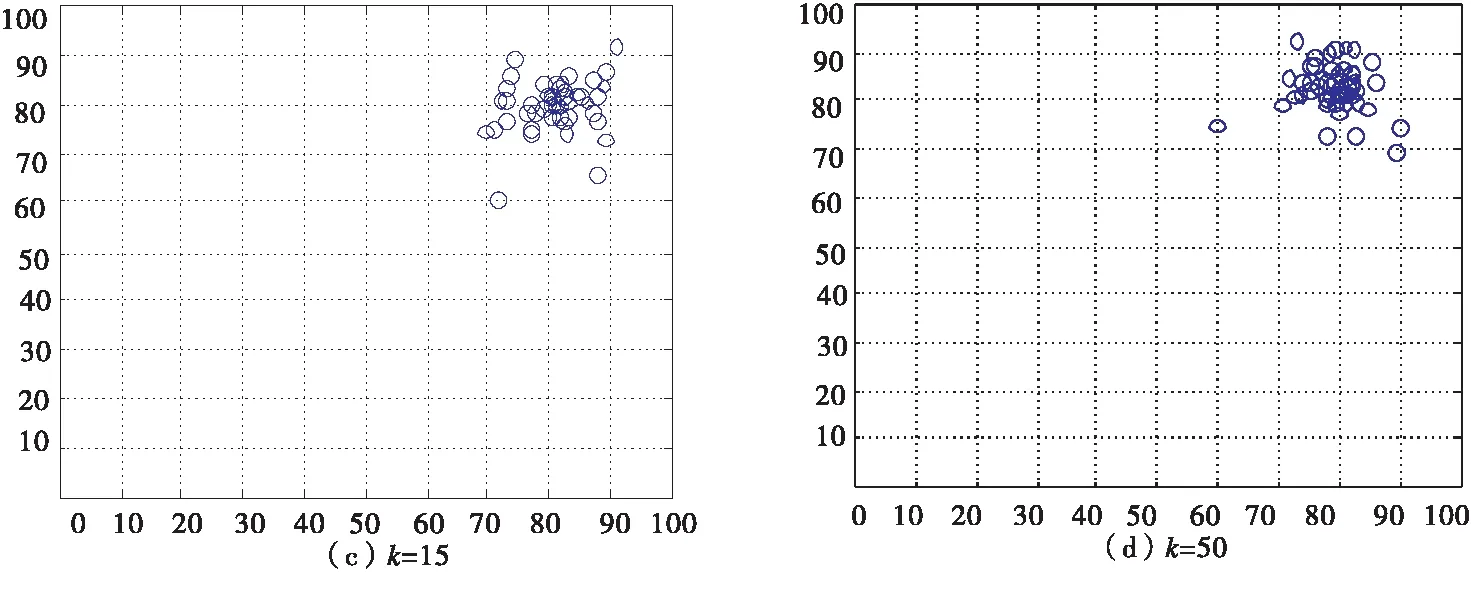
图5 无领导者的沙丁鱼惯性运动二维图

当ωa=0.2,ωr=0.2,ωo=0.1,ωt=0.5,ωf=0,诱惑源为(80,80,80)，恐惧源为(20,20,80)时，如图6所示，利用空间直角坐标系描述无领导者的沙丁鱼惯性运动情况.

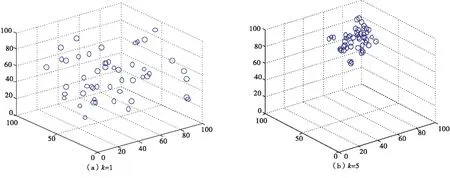
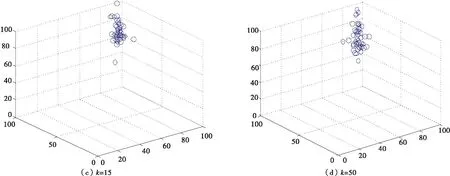
图6 无领导者的沙丁鱼惯性运动三维图

4 有领导者的沙丁鱼群非惯性运动模型

如图7所示,有领导者集群运动行为[7]的领导在运动过程中影响其他个体.外部环境作用领导者引导跟随者达到预期的目标，内部作用跟随者，因此对领导者和跟随者分别讨论.

图7 有领导者情况下对集群运动的影响作用

对于领导者设领导者在空间中的位置为X1=(x1,x2,…,xn).迭代k步，领导者的空间位置为X1(k)，速度大小为V1，速度方向为D1(k).假设在领导者的排斥区、一致区、吸引区分别有m1、m2、m3个个体，则吸引力产生的速度方向为

排斥力产生的速度方向为

一致力产生的速度方向为

诱惑力产生的速度方向为

危险力产生的速度方向为

则总速度方向为

D1(k)=λa1Da1(k)+λr1Dr1(k)+λo1Do1(k)+λt1Dt1(k)+λf1Df1(k)，

其中λa1,λr1,λo1,λt1,λf1∈[0,1],且λa1+λr1+λo1+λt1+λf1=1.

个体的速度为

V1(k)=V1·D1(k),

个体的新位置由当前位置和速度共同确定

X1(k+1)=X1(k)+V1(k).

对于跟随者设跟随者在空间中的位置为X2=(x1,x2,…,xn).迭代k步，跟随者的空间位置为X2(k),速度大小为V2，速度方向为D2(k).假设在跟随者的排斥区、一致区、吸引区分别有n1、n2、n3个个体，则排斥力产生的速度方向为

吸引力产生的速度方向为

一致力产生的速度方向为

则总速度方向为

D2(k)=λa2Da2(k)+λr2Dr2(k)+λo2Do2(k).

其中λa2,λr2,λo2∈[0,1],且λa2+λr2+λo2=1.

领导者对跟随者的吸引作用远大于跟随者对跟随者的吸引作用，跟随者由吸引力产生的速度方向为

Da2(k)=λa12Da12(k)+λa22Da22(k),

其中，Da12(k)为领导者对跟随者吸引作用产生的速度方向，Da22(k)为跟随者对跟随者吸引作用产生的速度方向，λa12和λa22为相应的权重因子，并λa12,λa22∈[0,1],λa12+λa22=1.

带入总加速度A2(k)可得

D2(k)=λr2Dr2(k)+λa2λa12Da12(k)+λa2λa22Da22(k)+λo2Do2(k).

个体的速度为

V2(k)=V2·D2(k).

个体的新位置由当前位置和速度共同确定

X2(k+1)=X2(k)+V2(k).

当诱惑源为(80,80)恐惧源为(20,20)时，如图8所示，利用二维坐标描述有一个领导者的非惯性运动情况.

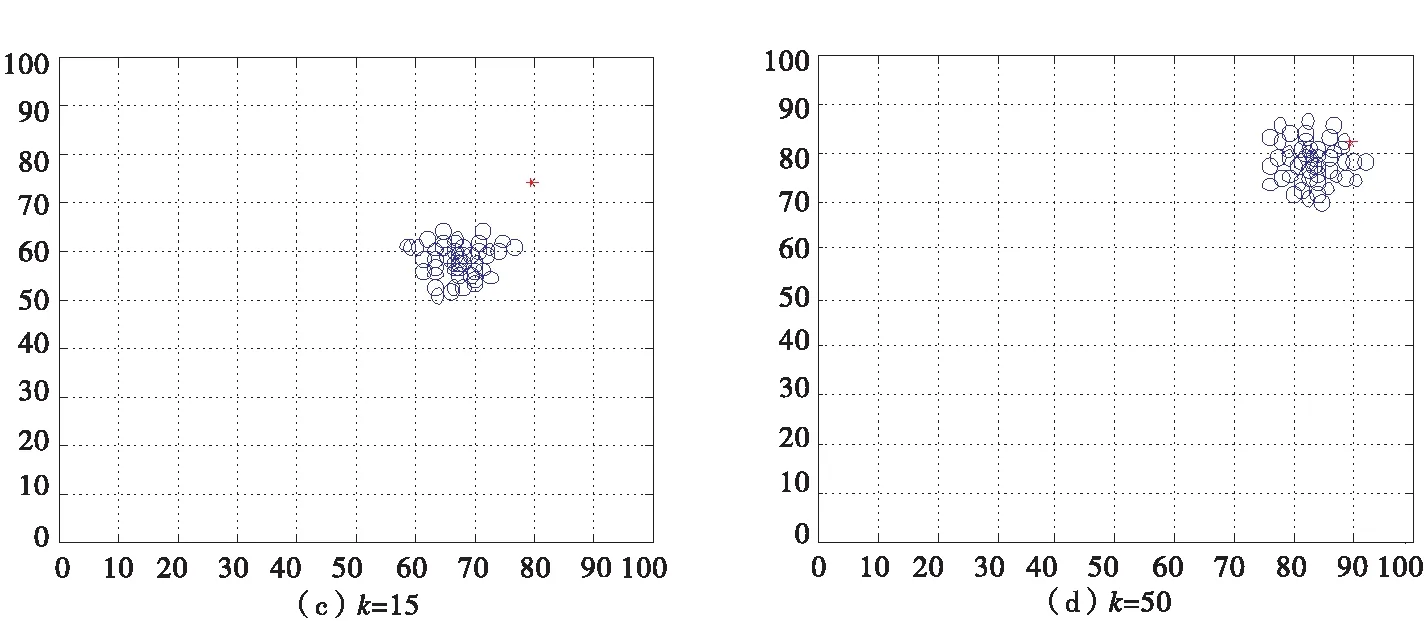
图8 有一个领导者的沙丁鱼非惯性二维图

当诱惑源为(80,80)恐惧源为(20,20)时，如图9所示，利用二维坐标描述有两个领导者的非惯性运动情况.

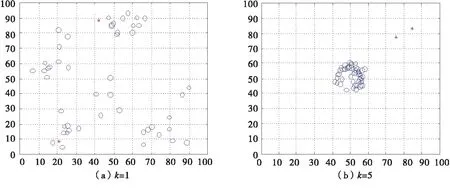
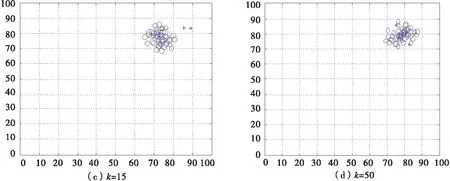
图9 有两个领导者的沙丁鱼非惯性二维图

5 沙丁鱼集群运动模型

在二维平面中,定义变量pi=(xi,yi,vi)来描述运动的个体,其中xi为个体i在坐标系中的横坐标，yi表示个体i在坐标系的纵坐标,vi表示个体i的运动的方向.如图10所示，运动的个体投影到地面[8]，把个体的运动看作点的运动.

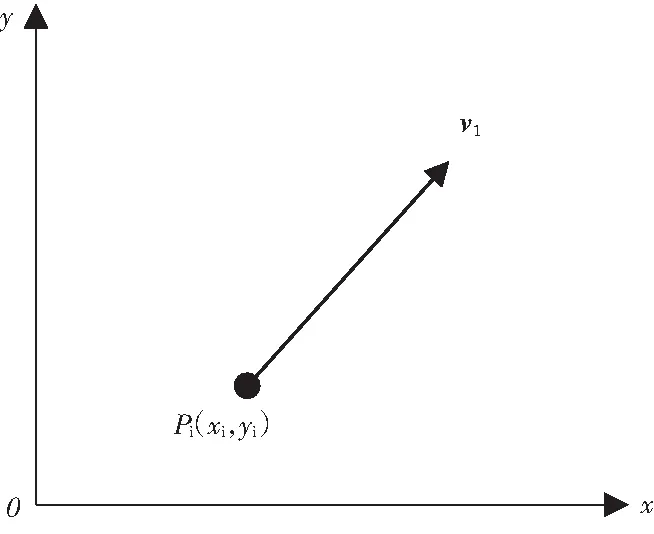
图10 个体投影在地面的图

讨论有n个个体的沙丁鱼群运动，建立n个个体的t时刻状态矩阵S(t)

其中vi为个体i的速度，根据状态条件建立状态方程.

距离条件为

位置中心一致性条件为

速度一致性

其中rmin为沙丁鱼个体之间的最小距离，RL为沙丁鱼个体之间的最大距离，m为个体i相邻个体的数量,vi为个体i的运动速度,vk为个体k的运动速度,μx为x方向的位置变动因子,μy为y方向的位置变动因子,δmax为运动速度最大误差.t+1时刻与t时刻有相同形式的状态矩阵,因此只需求得个体i的速度变化即可求得t+1时刻的状态矩阵

Pi,t+1(xi,yi)=Pi,t(xi,yi)+viΔt.

速度大小满足

vi(t+1)=vi(t)±Δvi,Δvi=ε1(vmax-vi(t)),ε1∈(0,1).

加速度满足

其中取逆时针方向为正方向，Δt为时间间隔,vmax为个体的最大速度,Δvi为个体i速度大小的变化量,Δθi为个体i速度方向的变化量,ε1为速度大小状态因子,ε2为速度方向状态因子，ε1,ε2均为(0,1)范围内任意的随机数，取ε1=0.6,ε2=0.1.假设集群是一个整体,海豚靠近过程中速度方向的变化省略不计,只考虑速度大小的变化，沙丁鱼躲避危险过程中速度大小和方向均有较大的变化,构建状态方程,方程迭代可得任意状态的方程矩阵,进而得到集群的运动情况如图11所示.

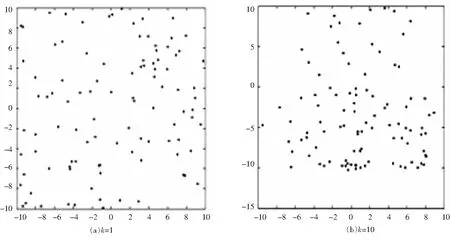
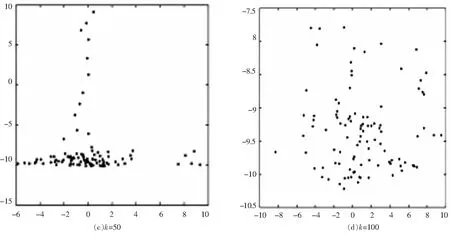
图11 沙丁鱼集群运动

6 海豚捕食沙丁鱼群模型

当海豚发现沙丁鱼群时，形成一个紧密的包围圈如图12所示，由一只海豚充当“轰赶者”[9]，将猎物向包围圈中驱赶,沙丁鱼群慢慢集中，海豚包围圈的不断收缩，此时海豚自动分组(圆圈上相对的两个点，比如说时钟上,12点和6点这两个点上的海豚为一组)，以顺时针方向依次入圈进食如图13所示，进食持续5分钟左右，海豚集体整齐浮出海面(仍然保持圆圈的阵形)，呼吸一次，又集体潜游下去，开始新一轮的进食.

图12 对鱼群包围 图13 分开进食

现以沙丁鱼群为球心，5-10米为半径，建立球体模型[10],以球心为坐标原点的球坐标与直角坐标的转化.

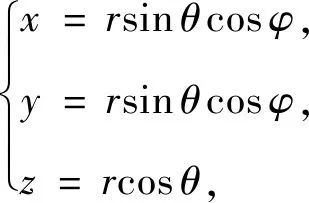
其中θ为球面上一点与球心连线与z轴的夹角,φ为连线投影到xy平面的直线与x轴的夹角.因此,球体模型的参数方程为

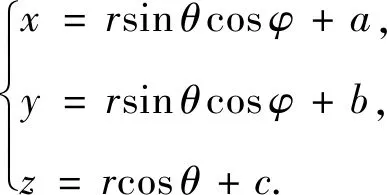
海豚的运动模型可类似于沙丁鱼群的集群模型，比鱼群集群模型的半径大，且为一个空心球体.则根据沙丁鱼群集群模型可得，海豚的运动模型的距离条件为

位置中心一致性条件为

(2)

速度一致性为

其中rmin为海豚捕到沙丁鱼的最小距离，视为固定值，RL为海豚对沙丁鱼群形成包围的最大距离，RL会随着海豚数量的增大而增大，m为海豚i感知范围内相邻个体的数量,vi为个体i的运动速度,vk为个体k的运动速度,μx为x方向的位置变动因子,μy为y方向的位置变动因子,δmax为运动速度最大误差.t+1时刻与t时刻位置变换表示为

Pi,t+1(xi,yi)=Pi,t(xi,yi)+viΔt.

速度大小满足

vi(t+1)=vi(t)±Δvi,Δvi=ε1(vmax-vi(t)),ε1∈(0,1).

加速度满足

其中取逆时针改变方向为正方向，Δt为t时刻与t+1时刻的时间间隔,vmax为个体的最大速度,Δvi为个体i速度大小的变化量,Δθi为个体i速度方向的变化量,ε1为速度大小状态因子,ε2为速度方向状态因子.

海豚对沙丁鱼群的包围简化为其距离d从大到小变化的过程.海豚自动分组[11](圆圈上比如时钟上12点和6点方向这两只海豚为一组)，海豚以顺时针的顺序依次入圈进食.该过程是 (2) 式基础上变动的过程，当海豚形成 (2) 式的球体时，会以对球体直径所在方向进行组队，然后沿顺时针方向依次进食，如图14所示.假设以A为起始位置，则AE两只海豚先向O点靠拢，捕食，依次BF、CG、DH，再回到原来的位置继续形成包围，集体直线上升到海面呼吸空气，再下潜到水中实施第二次包围，进食，如此循环.

7 沙丁鱼逃逸模型

在二维平面中，设k时刻海豚i位于S点，位置坐标为(xs(k),ys(k))，沙丁鱼群中心位于C点，坐标为(xc,yc)，假设海豚单位时间的步长为ls，则海豚与鱼群中心的距离为

海豚运动的向量单位化为

可得k+1时刻海豚的位置为

k时刻沙丁鱼i位于Nk点，位置坐标为(xn(k),yn(k))，根据安全距离最大化原则，沙丁鱼应在与其他沙丁鱼连线上远离海豚的方向.考虑安全角度最大化原则，沙丁鱼应沿着垂直于与其他沙丁鱼连线的中垂线方向远离海豚.综合逃逸原则[12]，沙丁鱼的逃逸方向与自身和海豚连线成θ角.如图15所示.

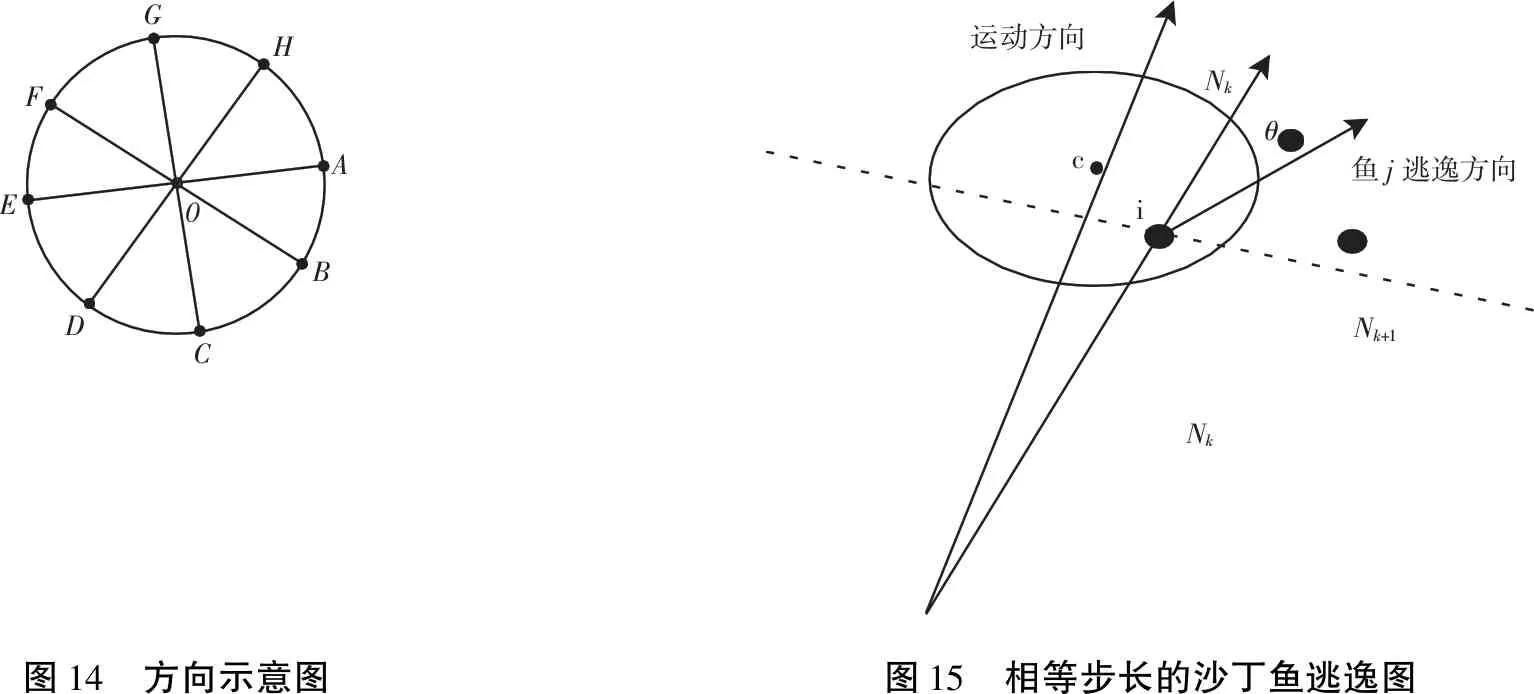
0GFEDCBAH运动方向鱼j逃逸方向NkNkNk+1ciθ图14 方向示意图图15 相等步长的沙丁鱼逃逸图

沙丁鱼与海豚的距离为

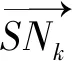
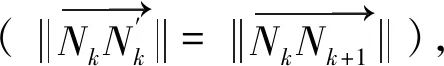
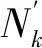
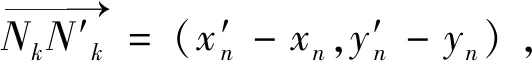
其中Nk+1的坐标为

通过不断迭代时间k得到海豚和沙丁鱼i的即时位置，并得到六只沙丁鱼对海豚的躲避运动轨迹如图16所示，沙丁鱼和海豚的步长相等.θ=60°时随着海豚的运动，沙丁鱼呈弧形躲避到了海豚的后方.如图17所示，增大沙丁鱼步长，进一步观察沙丁鱼的躲避运动轨迹，在速度允许的情况下沙丁鱼最终绕到海豚的正后方，找到最安全位置.

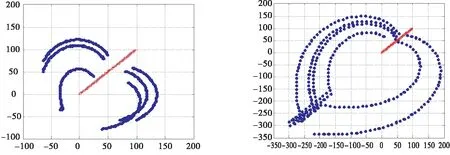
图16 相等步长的沙丁鱼逃逸图 图17 增大步长的沙丁鱼逃逸图

8 总结

本文利用数学语言描述海豚和沙丁鱼的位置变化情况，用速度与坐标来描述运动，将复杂系统的自组织过程转化为坐标系内质点的运动方向和坐标不断变化的数学问题；将鱼群逃逸数学化、向量化，语言准确科学，有效的追踪动物的运动状态，使得问题简单明了，易于解决.