关联代数上的(m,n)-Jordan导子和(m,n)导子

周斯名，袁 鹤

(吉林师范大学 数学学院， 吉林 长春 130000)

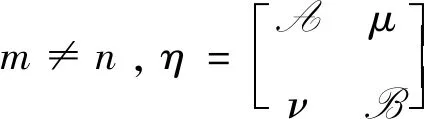
1 预备知识

定义1[1]设R是环或代数.如果一个可加(线性)映射φ:R→R满足对任意a,b∈R有φ(ab)=φ(a)b+aφ(b)，则称φ是导子.

定义2[1]设R是环或代数.如果一个可加(线性)映射φ:R→R满足对任意a,b∈R有φ(ab)=aφ(b)+bφ(a)，则称φ是左导子.

定义3[1]设R是环或代数.如果一个可加(线性)映射φ:R→R，满足对任意a,b∈R有φ(a2)=φ(a)a+aφ(a)，则称φ是Jordan导子.

定义4[6]设R是环或代数.如果一个可加(线性)映射且(m+n)(m-n)≠0，φ:R→R满足对任意a,b∈R有mφ(ab)+nφ(ba)=mφ(a)b+maφ(b)+nφ(b)a+nbφ(a)，则称φ是(m,n)导子.

定义5[1]设R是环或代数.如果一个可加(线性)映射φ:R→R且(m+n)(m-n)≠0，满足对任意a∈R有(m+n)φ(a2)=2maφ(a)+2nφ(a)a，则称φ是(m,n)-Jordan导子.

关联代数的概念最早由Ward[8]引出，之后人们对关联代数上的映射进行了研究[8-14].

定义6[9]若集合X中的二元关系≤满足以下两个条件：

(1)∀x∈X有x≤x

(2)∀x,y,z∈X,若有x≤y和y≤z⟹x≤z，

则称X是一个预序集，记作(X,≤)

定义7[9]取预序集X中的任意两个元素x，z，区间[x,z]定义为{(y∈X|x≤y≤z}.若预序集X中的所有区间都是有限的，则称X是局部有限预序集.

定义8[9]设R是含单位元的交换环(X,≤)是一个局部有限预序集，即≤满足自反性、传递性对任意的x,y∈X，且x≤y,至多存在有限个元素z∈X满足x≤z≤y,由此可在R上定义关于x的关联代数I(X,R):={f:X×X→R|f(x,y)}=0,若x≤y不成立}.

代数运算如下

(f+g)(x,y)=f(x,y)+g(x,y),

(rf)(x,y)=rf(x,y),

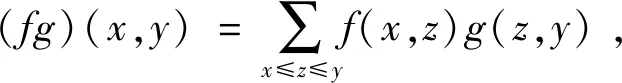
任意f,g∈I(X,R)，r∈R，x,y,z∈X，其中乘积fg在函数论中被称为卷积.

引理1[9]若δ满足δ(x,y)=δxy，x≤y其中δxy∈{0，1}是Kronecker符号，则δ是关联代数I(X,R)中的单位元.

给定一个f∈I(X,R)，有

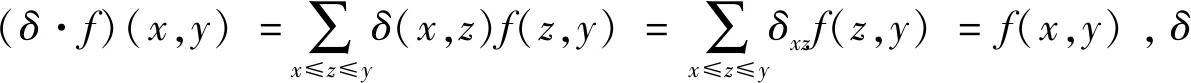
若任意的x,y∈X满足x≤y，则可定义关联代数I(X,R)上的基元exy

对任意的eij,ekl∈I(X,R),根据卷积定义我们有eijekl=δjkeil.

2 主要定理及证明

引理2[1]φ为代数R上的是(m,n)-Jordan导子，对于任意a,b∈R，则有

(m+n)φ(ab+ba)=2mφ(a)b+2mφ(b)a+2naφ(b)+2nbφ(a).

证明由φ：R→R为代数R上的是(m,n)-Jordan导子，则满足(m+n)φ(a2)=2maφ(a)+2nφ(a)a，将x=a+b代入上式则有(m+n)φ((a+b)2)=2m(a+b)φ(a+b)+2nφ(a+b)(a+b)，因此(m+n)φ(a2+ab+ba+b2)=(m+n)(φ(a2)+φ(ab)+φ(ba)+φ(b2)).由(m+n)φ(a2)=2maφ(a)+2nφ(a)a及线性代数φ，比较两式则有(m+n)φ(ab+ba)=2mφ(a)b+2mφ(b)a+2naφ(b)+2nbφ(a).

定理1 设(X,≤)是一个有限预序集，R是具有单位元的|(m+n)(m-n)|-扭自由的交换环.I(X,R)是在R上定义关于X的关联代数，设φ是关联代数上的线性映射φ:I(X,R)→I(X,R).若φ是(m,n)-Jordan导子，则φ恒等于零.

证明首先若φ是(m,n)-Jordan导子，则满足(m+n)φ(A2)=2mAφ(A)+2nφ(A)A，当A=0时，其中R是具有单位元的|(m+n)(m-n)|-扭自由的交换环，有φ(0)=0.

对于幂等元eii则有

(1)

对(1)右乘eii则有(m+n)φ(eii)eii=2meiiφ(eii)eii+2nφ(eii)eii，将其化简为

mφ(eii)eii=2meiiφ(eii)eii+nφ(eii)eii.

(2)

对(2)左乘eii有meiiφ(eii)eii=2meiiφ(eii)eii+neiiφ(eii)eii，将其化简为

meiiφ(eii)eii+neiiφ(eii)eii=0,

(3)

由m+n≠0且R是具有单位元的|(m+n)(m-n)|-扭自由的交换环，则有φ(eii)=0.

对于eij其中∀i，j∈X，i≤j且i≠j有

(m+n)φ(eiieij+eijeii)=2mφ(eii)eij+2mφ(eij)eii+2neiiφ(eij)+2neijφ(eii),

将其化简有(m+n)φ(eij)=2mφ(eii)eij+2mφ(eij)eii+2neiiφ(eij)+2neijφ(eii)，其中φ(eii)=0则有

(m+n)φ(eij)=2mφ(eij)eii+2neiiφ(eij).

(4)

对(4)右乘eii，(m+n)φ(eij)eii=2mφ(eij)eii+2neiiφ(eij)eii，化简为

nφ(eij)eii=mφ(eij)eii+2neiiφ(eij)eii.

(5)

对(5)左乘eii有neiiφ(eij)eii=meiiφ(eij)eii+2neiiφ(eij)eii，化简为meiiφ(eij)eii+neiiφ(eij)eii=0，其中m+n≠0，则有eiiφ(eij)eii=0，由(5)有nφ(eij)eii=mφ(eij)eii，其中m-n≠0且R是具有单位元的|(m+n)(m-n)|-扭自由的交换环.则有φ(eij)eii=0.由(4)有

(m+n)φ(eij)=2neiiφ(eij).

(6)

对(6)左乘eii有(m+n)eiiφ(eij)=2neiiφ(eij)，化简为meiiφ(eij)=neiiφ(eij).其中m-n≠0且R是具有单位元的|(m+n)(m-n)|-扭自由的交换环，则有eiiφ(eij)=0.可得φ(eij)=0.

引理3[10]设D:I(X,R)→I(X,R)是一个R-线性算子，则D是导子当且仅当D满足

其中系数eij∈B满足如下关系式

定理2 设(X,≤)是一个有限预序集，R是具有单位元的|(m+n)(m-n)|-扭自由的交换环.I(X,R)是在R上定义关于X的关联代数，设φ是关联代数上的线性映射φ:I(X,R)→I(X,R).若φ是(m,n)导子，则φ是导子.

证明首先若φ是(m,n)导子，则满足mφ(AB)+nφ(BA)=mφ(A)B+mAφ(B)+nφ(B)A+nBφ(A)，当A,B=0时其中m+n≠0，有φ(0)=0.

对于幂等元eii,当A,B=eii,由φ是(m,n)导子，则有mφ(eiieii)+nφ(eiieii)=mφ(eii)eii+meiiφ(eii)+nφ(eii)eii+neiiφ(eii),将其化简为(m+n)φ(eii)=(m+n)φ(eii)eii+(m+n)eiiφ(eii)，其中m+n≠0且R是具有单位元的|(m+n)(m-n)|-扭自由的交换环，则有φ(eii)=φ(eii)eii+eiiφ(eii),可得对于幂等元eii,φ是导子.

对于eij,当A=eii,B=eij,由φ是(m,n)导子，则有mφ(eiieij)+nφ(eijeii)=mφ(eii)eij+meiiφ(eij)+nφ(eij)eii+neijφ(eii)，将其化简为

mφ(eij)=mφ(eii)eij+meiiφ(eij)+nφ(eij)eii+neijφ(eii).

(7)

当A=eij,B=eii,由φ是(m,n)导子，则有mφ(eijeii)+nφ(eiieij)=mφ(eij)eii+meijφ(eii)+nφ(eii)eij+neiiφ(eij)，将其化简为

nφ(eij)=mφ(eij)eii+meijφ(eii)+nφ(eii)eij+neiiφ(eij).

(8)

(7)、(8)相加得(m+n)φ(eij)=(m+n)φ(eii)eij+(m+n)eiiφ(eij)+(m+n)φ(eij)eii+(m+n)eijφ(eii),其中m+n≠0且R是具有单位元的|(m+n)(m-n)|-扭自由的交换环，则有

φ(eij)=φ(eii)eij+eiiφ(eij)+φ(eij)eii+eijφ(eii),

(9)

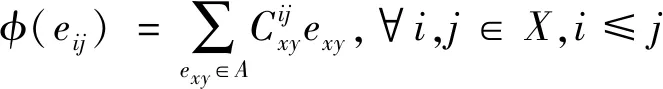
由卷积定义将其化简为

(10)

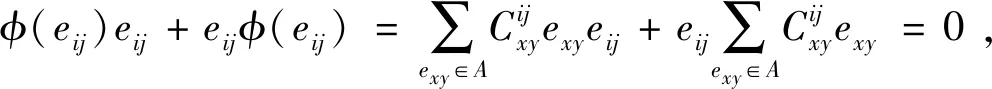
(11)

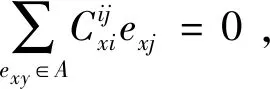
同样地，当A=eij、B=ejj,由φ是(m,n)导子，则有mφ(eijejj)+nφ(ejjeij)=mφ(eij)ejj+meijφ(ejj)+nφ(ejj)eij+nejjφ(eij)，将其化简

mφ(eij)=mφ(eij)ejj+meijφ(ejj)+nφ(ejj)eij+nejjφ(eij).

(12)

当A=ejj，B=eij,由φ是(m,n)导子，则有mφ(ejjeij)+nφ(eijejj)=mφ(ejj)eij+mejjφ(eij)+nφ(eij)ejj+neijφ(ejj)，将其化简为

nφ(eij)=mφ(ejj)eij+mejjφ(eij)+nφ(eij)ejj+neijφ(ejj).

(13)

(12)和(13)相加得(m+n)φ(eij)=(m+n)φ(eij)ejj+(m+n)eijφ(ejj)+(m+n)φ(ejj)eij+(m+n)ejjφ(eij)，其中m+n≠0且R是具有单位元的|(m+n)(m-n)|-扭自由的交换环，则有

φ(eij)=φ(eij)ejj+eijφ(ejj)+φ(ejj)eij+ejjφ(eij).

(14)

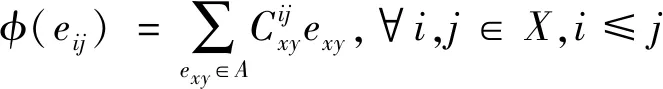
由卷积定义将其化简为

(15)

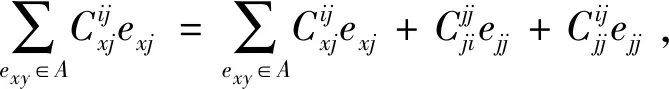
3 结论

本文主要研究了关联代数I(X,R)上的(m,n)-Jordan导子和(m,n)导子.本文利用组合方法研究算子代数，为后续相关内容的研究提供新的方法.