基于排队论的机场出租车决策模型研究
——以浦东机场为例
徐士博,程晓燕,孙闯闯
(甘肃农业大学理学院,甘肃 兰州 730030)
1 引言
随着我国科技、经济的发展进入新时代,我国的科技力量和经济水平得到空前的提升,人民的物质生活水平也随之不断提高,人们选择飞机这种交通工具作为远程出行方式的比重也在不断增加。因为飞机不仅耗时短,还具有更加安全舒适的优点,这也是人们选择飞机出行的重要原因之一。由于越来越多的人们选择飞机作为自己旅途出行的主要交通工具。那么乘坐哪种交通工具是最快速有效离开机场成了人们选择的难题。与离开机场的众多交通工具相比,机场出租车具有即走即停,方便快捷的特点,这是许多旅客选择乘坐出租车作为自己离开机场的主要原因之一。随之而来的是机场出租车也成为许多旅客尤其是商务旅客的首选。但是随着越来越多的人选择乘坐出租车离开机场的同时,有时会出现出租车排队等待乘客和在客流量较大的时候离机乘客打不到出租车的情况。这就会给机场、旅客和出租车司机三者之间带来不必要的困扰,给出行的人们带来不必要的麻烦,同时出租车司机的载客方式及机场管理部门出台的下机旅客离开机场的措施也直接影响了机场客流量的疏导和机场出租车司机的收益。针对上述情况就要求机场管理部门和出租车司机之间的调度要有一个合理的规划,使得进站和出站的旅客达到一个相对平衡的状态。本研究以上海浦东国际机场为例,探讨如何在合理安排乘客上车的情景下设置“上车点”,确保车辆和乘客的安全,以达到最高的乘车效率。
2 机场出租车排队论模型
2.1 出租车多点双向式排队系统服务状态
机场出租车载客区多点双向式排队服务系统是指在保证机场乘客安全的前提下,在机场出租车载客区设置一条离机乘客只出不进的出租车通道,同时要求载客的出租车在通道两旁等候区等待上车的乘客,机场乘客从两旁乘车,即叫即走,这样不仅可以增加载客出租车的数量,也增加了机场乘客即时打到出租车的概率,加快了机场乘客离开机场的速度,解决了机场乘客打车难的问题,也缓解了机场客流大的压力。同时尽量使得机场出租车司机的收益得到均衡,让出租车司机的收益也能达到最大化。本研究假设上海浦东国际机场载客区的上车方式为多点双向式排队上车,下机的旅客从机场出租车载客区两侧等待出租车。因为上海浦东国际机场客流量大,此上车方式与普通的单点式上车方式相比来说,可以更好地缓解上海浦东国际机场的客流压力。如图1所示,图标为上车点,下机乘客从出站口出来后,按照双箭头指示,在行车道的两侧等候出租车;图中分别有两条行车道,并且机场载客区乘车点分布在行车道的两旁,出租车的进站方向为从左到右,离开机场的乘客的进入方向与机场出租车进站的方向保持一致,这样就能尽可能地保证离开机场乘客的安全,并且该车道为单行车道,即出租车从左侧驶入接到乘客后立即从右侧离开。

图1 出租车排队服务系统
2.2 排队模型
依据排队论[1],在排队系统中将顾客和机场载客区服务台可以分为繁忙期、空闲期和休息期。繁忙期是指在排队系统中机场乘客人数从1开始到再次为0的这一时期,即有机场乘客在排队系统中等候或正在排队。与繁忙期相对的是机场乘客人数再次从0到1的过程,即当排队系统空闲时,称为空闲期[2-5]。与前面两种状态都不相同时,也就是机场出租车载客区服务台处于不在工作的状态时为休息期。排队系统的繁忙程度可以用繁忙率ρ这个数值来定量表示,是指系统中机场乘客到达率与服务率之比。乘客人数越多,排队系统就越繁忙。当数值大于1时,机场出租车载客区的排队系统将处于无限繁忙的排队状态[6-8]。计算公式如(1)式。

式中:λ代表机场出租车载客区设置的上车点数,机场出租车乘客的平均到达速率;μ为机场出租车载客区单个上车点的平均上车率;Cμ为机场出租车载客区多个上车点的平均上车率。
根据排队理论,建立了机场出租车站点排队系统的排队模型[9-10]。当机场出租车载客区的排队系统处于繁忙期,且ρ<1,则此时的排队系统处于稳定的状态,不会出现机场出租车载客区无限排队的现象。在上述背景下对机场出租车载客区排队系统中的乘客进行建模。
在系统达到稳定时,机场出租车载客区C个服务台并联工作,系统中出租车乘客人数为n的概率如下:

用系统中乘客排队的队长以及逗留时间对系统进行分析,得:

式中:P0(C)、Pn(C)分别代表机场出租车载客区C个服务台并联工作,系统中出租车乘客人数分别为0和n的概率;Ls和E(Ws)分别代表乘客排队的队长及逗留时间。
2.3 排队系统优化
假设乘客等待时间总成本为Z1=αLs,机场出租车载客区上车点的建设成本为Z2=βC,其中α为每个乘客单位时间的等待时间成本,β为单个机场出租车载客区服务台的服务时间成本与单个上车点的建设费用。当乘客等待时间总成本与出租车上车点建设成本之和最小时,机场出租车载客区排队系统达到最优状态[11]。

式中:Z(C)为乘客等待时间总成本与机场出租车载客区上车点建设成本之和;Ls(C-1)、Ls(C)、Ls(C+1)分别代表乘客人数为(C-1)、C、(C+1)时乘客的排队对队长。
3 上海浦东机场出租车排队服务系统
上海浦东国际机场是我国华东地区最大的枢纽机场,客吞吐量也一直稳居我国机场的前三位[12-14]。研究上海浦东国际机场对于我国的一些大中型机场的出租车载客以及人员疏通问题都具有一定的指导意义。旅客选择乘坐出租车离开机场是主要的方式之一,因此对出租车载客进行合理规划及对载客区上车点的设置进行研究,为做好上海浦东国际机场的客流量疏导具有积极的意义,同时也可以有效地解决机场出租车排队载客的现实问题。通过对上海浦东国际机场具体相关数据的调查与分析,给出了相应的解决方案和建议,以达到缓解上海浦东国际机场客流量过大的问题。
根据上海浦东国际机场出租车载客区的多点双向式上车方式,运用优化后的费用决策排队模型。对上海浦东国际机场的出租车接载区的乘客到达率λ与上车率μ进行了统计调查(表1),并假设乘客等待时间成本与服务台成本比值为1∶6。表2是上海浦东国际机场统计调查的相关数据,并利用相关数据计算所得出的结果。
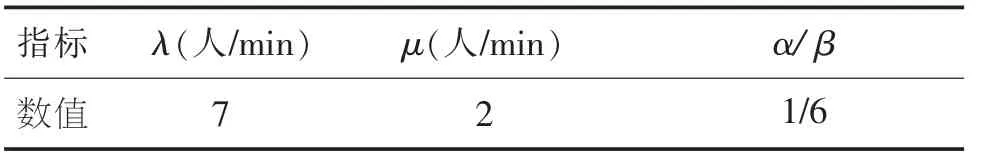
表1 排队系统到达率与服务率
利用从上海浦东国际机场官网查询到的旅客客流量和航班信息带入排队论理论模型中,计算得到不同乘客人数情况下出租车服务台的排队情况,见表2。

表2 浦东国际机场服务台个数计算数据
其中根据表2得到的数据结果,利用上述费用决策理论模型对上海浦东国际机场的出租车排队服务系统进行优化,计算结果见表3。
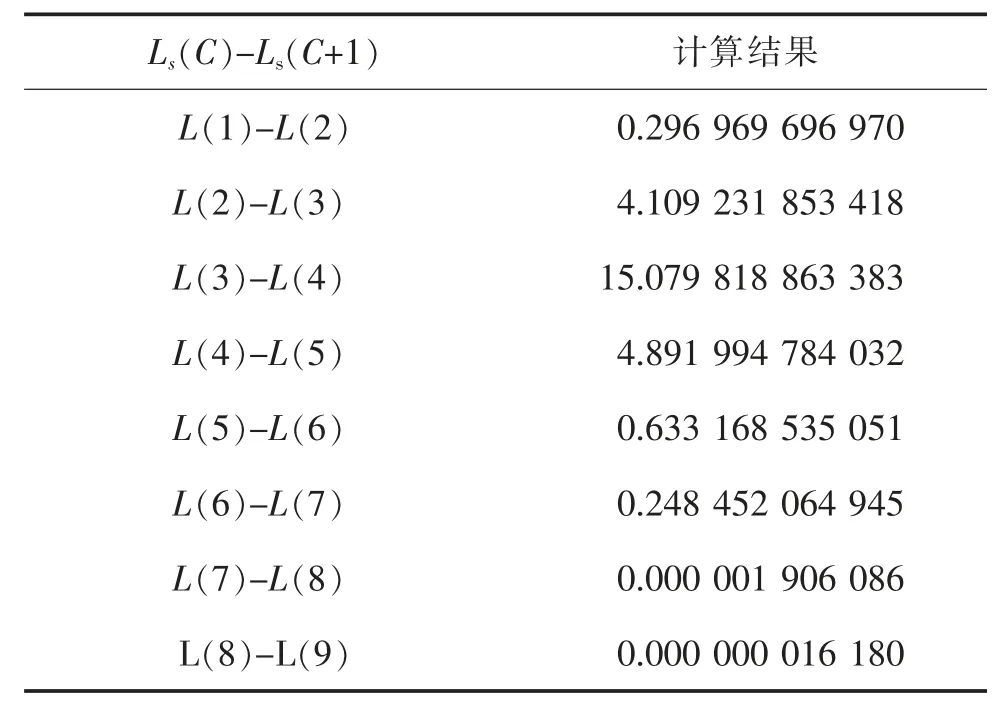
表3 费用决策模型计算过程
根据表3的计算结果可得,当机场的出租车载客区设有7个上车点时,满足公式:Ls(C-1)-Ls(C)≥≥Ls(C)-Ls(C+1),排队论系统的费用之和达到最小。此时的上海浦东国际机场总的乘车效率达到最高。
4 结论
(1)本研究通过对上海浦东国际机场客流量和出租车载客区的建设规划来分析解决旅客出行和出租车司机载客的决策问题。以机场出租车载客区服务点布局模拟“上车点”位置,并根据排队理论建立模型,通过查找实际的上海浦东机场排队系统的到达率和服务率,将具体数据带入排队模型中得到了乘车效率最高的最佳“上车点”数为7个,此时能够有效地缓解上海浦东国际机场旅客离开机场和出租车司机的载客决策问题,使二者之间的效率都达到最高水平。
(2)对于与上海浦东国际机场出租车载客区同样都是多点式双向上车的机场来说,可以采用本研究规划方式来进行出租车载客区的规划与建设。我国其他机场可以上海浦东国际机场为例,选择适合不同机场的参数,设置最佳的机场载客区上车地点和上车点数来方便机场乘客的出行并节约出租车的等待时间,在解决出行问题的同时,使得出租车司机也能获得一定的经济收益,促使机场的运营更加合理有效。
(3)本研究中将机场内出租车上客区的排队系统进行了简化,仅考虑了上客区的乘客排队情况,而现实中出租车排队服务系统通常存在双端排队模式。因此,在后续的研究中将综合考虑多个因素,如出租车排队情况、候客出租车停车位的设置情况等,在此基础上对排队系统进行优化,进而提高出租车乘客的离站效率。

