基于模型参考自适应的柴油机转速控制研究

宋恩哲，宋体康，马 骋，姚 崇，刘昭璐

（哈尔滨工程大学动力与能源工程学院，哈尔滨 150001）

0 概述

柴油机因具有较高的热效率，仍是民用船舶和军用船舶的主要动力。柴油机系统是典型的非线性系统，转速受众多因素的影响。而柴油机转速控制是船舶动力系统控制的基础，需要研究适应性更强的柴油机转速控制策略。目前，大多数船用柴油机采用比例积分微分（proportion integration differentiation，PID）控制算法，该算法理论简单，鲁棒性强［1］，且易于实现，但传统PID 的控制参数是线下整定的且无法在线调整。船舶在大海中航行处于复杂多变的环境，传统PID 控制无法全面地将因素考虑在内。自适应控制技术的出现和快速发展为柴油机转速控制提供了新的解决方法，模型参考自适应控制（model reference adaptive control，MRAC）成为了新的研究方向。文献［2］中提出了最小控制综合（minimalcontrol synthesis，MCS）算法，该算法源于MRAC 算法，在被控对象参数时变、未建模动态及未知扰动等非线性问题存在下，能够使被控对象达到良好的控制效果［3］。文献［4］中围绕六相感应电机的高性能无速度传感器驱动问题，采用二阶滑模模型参考自适应系统估计器，实现了六相感应电机的无速度传感器优化直接转矩控制。文献［5］中研究变惯量负载永磁同步电机时，针对惯量变化引入的位置响应超调和震荡，采用了一种强鲁棒性的模型参考自适应位置控制策略，不依赖于电机机械参数精确建模，在负载惯量发生大范围变化时仍能保持较好的控制性能。文献［6］中针对变循环航空发动机多变量控制、建模不确定性及外部随机干扰等问题，进行了建模不确定下模型参考自适应控制方法及变循环航空发动机应用研究，实现了系统跟踪误差渐进为零的目标。文献［7］中以涡扇发动机为研究对象，设计了多变量模型参考自适应控制方法并针对动态性能提升、鲁棒性加强和非线性补偿等问题分别改进，应用于高压转速和压比双变量控制系统。文献［8］中在研究电子节气门控制时，为了应对系统参数的不确定性，采用基于模型参考自适应控制的电子节气门控制方法，仿真结果表明其能够使电子节气门实现快速准确的位置跟踪控制。文献［9］中针对多变量系统存在不确定性导致的控制性能下降问题，提出了一种基于最优控制律的增广模型参考自适应控制器补偿设计方法，其符合发动机控制系统技术要求，并改善原系统在不确定时的不稳定控制效果。文献［10］中为了更好地调节转速而对电控喷油器展开了参数优化匹配，得到了关键结构参数对电控喷油器针阀动态响应特性的影响权重和最佳参数组合。文献［11］中为提高发电机组用发动机的抗干扰能力，设计了一种基于扩张状态观测器变结构自抗扰控制器，其能够满足发电机组稳态及动态频率特性需求，且相对传统控制在抗扰能力上有所提高，满足跟踪需求。

船舶柴油机具有复杂的时变、不确定性并受众多参数影响，要求其转速控制具有很强的适应性。本研究中采用MRAC 策略拓展的离散时间积分最小控制综合（discrete-time minimum control synthesize integration differentiation，PID）算法控制柴油机转速，该控制算法对系统参数的依赖性不高，且不需要大量的标定，本研究可为船用柴油机的转速控制提供一种新的有效途径。

1 船用柴油机系统模型

被控对象为带高压共轨系统的柴油机。将柴油机系统分为燃油子系统、气缸子系统、进排气子系统、动力学子系统和辅助子系统。新鲜空气经压缩机压缩后进入中冷器冷却，冷却后的低温气体通过进气管进入气缸。经活塞压缩让缸内温度升高，使喷射的燃油被点燃，缸内气体膨胀做功，推动活塞带动连杆和曲轴输出动力。废气驱动涡轮旋转，使压缩机压缩吸入新鲜空气。根据平均值建模原理，基于Simulink 建立了高压共轨柴油机数学模型，对控制算法进行初步验证，详细的建模过程见文献［12］，柴油机仿真模型如图1 所示。柴油机结构参数见表1。

图1 柴油机系统仿真模型

2 DTMCSI 算法

假设被控对象即柴油机转速控制系统数学模型以式（1）表示。

式中，x、u分别为系统的状态和控制输入，x∈RN，u∈R；N为状态空间的维数；A为系统参数矩阵，A∈RN×N；B为输入参数矩阵，B∈RN×1；D为扰 动向量；k为时刻。任何未建模项、外部扰动和参数变化都包含在D中。

参考模型为线性时不变系统，其结构如式（2）所示。

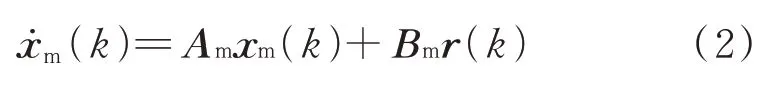
式中，xm、r为某个期望的参考信号，xm∈RN，r∈R；m 为参考模型的简称；矩阵Am和Bm以与系统相同的标准形式给出。

参考模型与被控对象形式相同但不包括干扰项。DTMCSI 算法的标准控制律u(k)如式（3）所示。

式中，uMCS(k)为标准MCS 算法的控制律；uI(k)为减少噪声等干扰的自适应控制律；Kp(k)、Kr(k)、KI(k)为自适应控制增益；xI(k)为积分跟踪误差；α、β、αI和βI分别为标量自适应权重；x(k)为k时刻系统的状态；r(k)为参考模型的输入；ye为输出的误差信号；Be=[0…0 1]T∈Rn；P为对称正定矩阵；xe(k)为系统状态x(k) 与参考模型状态xm(k) 偏差。综上可得式（12）。

式中，Q为对称正定矩阵。

详细的稳定性证明过程见文献［13］。

3 DTMCSI 算法转速控制器

船用柴油机转速微分方程如式（13）［14］所示。

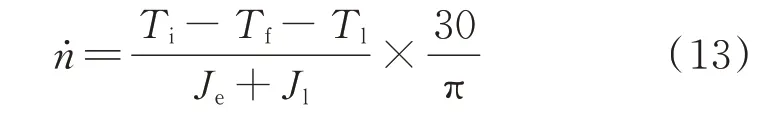
式中，n为柴油机转速，r/min；Ti为柴油机的指示转矩，N·m；Tf为柴油机轴的摩擦转矩，N·m；Tl为负载转矩，N·m；Je为活塞和连杆、曲轴和飞轮的柴油机轴系统的转动惯量，kg·m2；Jl为负载的总转动惯量，kg·m2。

指示转矩由每个气缸的燃料燃烧产生，其计算式如式（14）所示。

式中，m为每循环喷射到每个气缸中的燃料质量；ηi为总指示效率，它是柴油机转速和空燃比的函数；Hu为柴油的低热值；Ncyl为气缸数量；Nst的值取决于柴油机的类型，二冲程柴油机和四冲程柴油机分别取1 和2。

摩擦转矩根据经验公式计算，如式（15）所示。

式中，Vd为总排量，L；c1、c2为试验系数。转速的一阶微分方程如式（16）所示。

选择式（17）～式（19）作为参考模型，DTMCSI算法转速控制器原理框图如图2 所示。

图2 DTMCSI 算法转速控制器原理框图

此时可以采用DTMCSI 算法，但在实施控制律式（3）时，必须考虑3 个问题：（1）参考模型被离散化，采样时间设为ts=0.001 s，保证离散时间稳定。（2）参考模型的输出给出了理想的控制效果曲线，且不在乎被控对象的数学模型及参数是否已知。将目标值与实际值的偏差代入DTMCSI 算法控制律中并辅以前馈信号以达到控制效果，其控制增益Kp、Kr、KI随跟踪误差与参考信号自适应变化以确保系统全局渐近稳定。在实施DTMCSI 策略时，调节式（5）～式（7）中的自适应增益的标量必须试验性地选择，作为收敛时间和控制律的反映性之间的权衡。根据DTMCSI 经验［15］，设置α/β=10。为了进一步减少要调整的参数数量，对积分权重也进行同样设置，即αI/βI=10。此外，令αI/α=0.06，在自适应积分作用不占主导地位的情况下提高了闭环稳定性。这样在整个自适应控制策略中需要调节的参数仅剩参数α。（3）在参考模型的输入快速变化期间，引入一阶滤波器来降低转速的跟踪误差。为了限制反馈信号的噪声，对瞬时转速也引入一个一阶滤波器，该滤波器的带宽调整为关于柴油机转速的函数。

4 离线动态模拟测试

4.1 模型仿真精度校验

为了模拟真实的柴油机工况，验证了柴油机模型的准确性。选取25 组开环试验的喷油数据与模型仿真数据进行比较，结果如图3 所示。最大误差为9.8%，平均误差仅为1.5%，表明所建立的柴油机平均值模型能够用于控制算法的离线验证。

图3 模拟与试验喷油量的比较

4.2 转速跟踪性能仿真

为了验证转速自适应控制算法的控制性能，在船用柴油机的常见工况点进行仿真测试，并与传统PID 控制进行比较，仿真包括起动过程、稳态运行过程、加减速过程。

首先，让起动电机拖动柴油机运转，直到柴油机达到一定的转速；这时柴油机进入开环控制阶段，开环工况下固定循环喷油量将柴油机加速至转速闭环设定点；之后，系统使用控制算法进行转速闭环控制。

图4 为不同控制算法下柴油机加速和减速过程的跟踪效果。整个过程中柴油机由起动机驱动，转速达到100 r/min（即点A）时，起动马达分离，柴油机进入开环控制阶段，该阶段介于点A 和点B 之间。在开环阶段，气缸中按预设的循环喷油量喷油。当柴油机加速到转速闭环设定点B 时，控制系统根据转速偏差调整喷油量，使柴油机转速达到目标转速。从图4 可以看出，所采用的控制算法能够满足柴油机运行过程的控制需要，并且具有良好的控制精度。为了进一步考察其实际应用潜力，基于快速控制原型系统设计了试验台架，并进行试验测试。

图4 空载加减速仿真结果比较

5 台架试验验证

5.1 试验台系统

基于快速控制原型的柴油机试验台由柴油机、电涡流测功机、Micro-AutoBox、上位机监控和报警系统组成，试验台架整体结构如图5 所示。从柴油机采集的信号经过信号处理装置的接收和处理。这些信号包括曲轴、凸轮轴信号、轨压信号及来自其他辅助系统的温度和压力信号，用于掌握柴油机的运行状态，维持柴油机的正常工作，并确保系统能够安全可靠地运行。将转速控制算法下载编译到快速控制原型系统中，以设定的目标转速和曲轴传感器采集到的实际转速之间的偏差作为控制系统的输入，经实时处理单元准确快速地计算后，控制系统输出循环喷油量。动力驱动单元驱动执行器（即喷油器）以改变进入气缸的循环喷油量，进而实现对转速的精确控制。电涡流测功机的作用是提供试验所需的负载转矩。基于Control-Desk 软件的上位机监控平台可以在线调整控制参数，实时监控柴油机运行状态。该试验台可实现柴油机起动、停止、加减速、突加突卸负载等工况。

图5 柴油机测试台架结构图

根据中华人民共和国国家标准GB/T 3475—2008 中船舶推进主机的测试要求，对转速自适应控制算法的控制性能进行了台架试验，试验验证分为稳态特性测试和动态特性测试两部分。

5.2 稳态特性测试

稳态特性测试是转速控制系统在稳定工况下的控制性能，试验和测量在推进特性和空载工况下进行。

以转速波动率为稳态下柴油机转速控制稳定性的指标。在柴油机负载不变的情况下，测量一定时间间隔内（不少于1 min）的最大转速nmax和最小转速nmin，并以两者之差除以标定转速nr的两倍，结果即为转速波动率υ。

5.2.1 空载转速波动试验

空载转速波动率在空载且转速为标定值的50%、80% 和 100%下进行试验，并将传统 PID 和DTMCSI 算法的控制效果进行比较。两种控制算法下分别进行不少于1 min 的试验，自适应算法下计算步长为0.001 s，PID 算法下计算步长为0.01 s，选取各工况的20 s 试验数据，比较结果如图6 所示。从图6 中可以看出，自适应算法的转速波动率较小，稳态特性比PID 控制效果好。经过计算发现，自适应控制算法在目标转速1 500 r/min 下转速波动率为0.26%；目标转速1 200 r/min 下转速波动率为0.15%；目标转速750 r/min 下转速波动率为0.3%。PID 控制算法在目标转速为1 500 r/min、1 200 r/min、750 r/min下，转速波动率分别为0.54%、0.63%、0.61%。所有工况下的自适应控制算法的稳态波动率仅为普通PID 控制算法的一半。

图6 空载下不同控制器转速波动率比较

5.2.2 推进工况转速波动试验

推进工况试验与空载相似，在柴油机试验台架上进行了不同工况下的稳态转速波动率测试试验。根据GB/T 3475—2008 的要求，柴油机运行于推进工况，在转速为标定值的63%、80%、91% 和100%工况下进行试验。图7 为推进工况下不同控制器转速波动率比较。从图7 可以看出，自适应控制算法在加载时仍然保持良好的稳定性。

图7 推进工况下不同控制器转速波动率比较

相比之下，传统的PID 控制效果较差，但也在可接受的范围内。随着转速的增加，PID 算法控制下的转速波动率呈上升趋势，但DTMCSI 自适应算法的控制性能更稳定。自适应控制算法在目标转速1 500 r/min 下的转速波动率为0.34%；目标转速1 365 r/min 下的转速波动率仅为0.26%；目标转速1 200 r/min 下的转速波动率为0.29%；目标转速945 r/min 下的转速波动率为0.35%。PID 控制算法在目标转速为1 500 r/min、1 365 r/min、1 200 r/min、945 r/min 下，转速波动率分别为0.86%、0.73%、0.67%、0.52%。DTMCSI 自适应控制算法下转速波动率远远小于PID。

5.3 动态特性测试

5.3.1 转速动态跟踪测试

转速动态跟踪特性试验方式与离线仿真相同，在空载下目标转速分别取300 r/min、600 r/min、900 r/min、1 500 r/min 进行试验。为了满足船舶柴油机实际航行中运行要求，变速过程按照固定的加减速速率30 rad 进行调速，避免超调损坏柴油机系统，保证可靠性。

图8 是传统PID 控制算法和DTMCSI 自适应算法控制下的转速跟踪效果的比较。从图8 中可以看出，PID 控制超调量较大，DTMCSI 自适应算法在整个过程中更令人满意。这一结果也与稳态转速波动试验的结果一致，再次证明了DTMCSI 控制算法的稳定性。图9 是相应转速下循环喷油量的比较。由图9 可以看出，DTMCSI 自适应算法具有较小的波动，说明其控制稳定性更好。

图8 空载加减速试验结果比较

图9 空载下循环喷油量的比较

5.3.2 负载突变试验

根据GB/T 3475—2008 的要求，进行柴油机动态特性试验。用负载突变试验验证控制器的鲁棒性。以瞬时调速率δd为柴油机转速在负载突变下动态响应性能指标，其值的大小与控制器的鲁棒性成反比。柴油机在整定稳态调速率后突卸（或突加）一次标定负载后的最大（或最低）转速与负载变化前稳定转速的差占标定转速的百分比，由公式（21）进行计算。转速稳定时间τ是在系统受到扰动后再次达到稳定状态所需的时间。

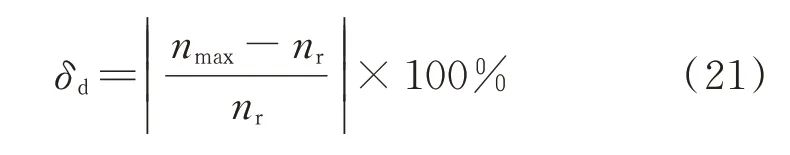
突卸、突加负载后的转速波动如图10 所示，相应的自适应参数变化如图11 所示。试验在标定工况点（1 500 r/min、235 kW）进行了3 次，图中仅展示1 次结果。3 次试验结果如表2 所示，、τ+分别为突卸负载时的调速率和稳定时间，δd-、τ-分别为突加负载时的调速率和稳定时间。每次测试的结果差异很小，这也验证了DTMCSI 自适应控制算法的稳定性。

图10 标定转速下负载突变试验

图11 负载突变下自适应参数变化

表2 柴油机转速动态跟踪特性试验

各精度指标如表3 所示。试验测试结果表明突卸负载转速瞬时调速率的平均值为2.33%，比表3中规定的1 级指标（5%）低近50%。稳定时间几乎接近1 级规定的2 s。突加负载转速瞬时调速率性能甚至更好，尽管这会延长稳定时间。总体而言，DTMCSI 自适应控制的瞬态调速指标满足2 级精度要求，个别（如瞬时调速率）已达到1 级精度要求。

表3 不同精度指标

通过试验以充分验证控制算法的可行性在柴油机推进工况下，选取标定转速的63%、80% 和91%的3 种转速工况进行验证，相应工况下转速和喷油量随负载变化情况如图12～图14 所示。

图12 标定转速的63%工况下负载突变试验结果

图13 标定转速的80%工况下负载突变试验结果

图14 标定转速的91%工况下负载突变试验结果

根据GB/T 3475—2008 的要求，当负载从标定负载变为空载或从空载变为标定负载时，稳定空载转速与标定转速之差的绝对值占标定转速的百分比为稳态调速率δst，它体现了控制器在负载突变后维持稳定转速的能力。

式中，ni为空载稳态转速。

试验中稳态调速率设定为2.6%，图15 为稳态转速调速率测试的结果。测试期间，柴油机在标定工况下运行。在7 s 时，突卸负载，转速快速上升，达到空载速度后稳定下来。卸载负荷后，循环喷油量迅速减少到19.8 mg。

图15 转速稳态调速率试验结果

6 结论

（1）采用DTMCSI 算法进行柴油机转速控制，并按照GB/T 3475—2008 的要求进行试验验证，试验结果表明DTMCSI 算法在控制柴油机转速方面自适应性强，仿真试验中得到的自适应参数同样也适用于实机试验。

（2）在稳态试验中，转速稳态波动率在全工况范围内小于0.4%，满足2 级精度指标。

（3）在动态试验中，采用DTMCSI 的自适应转速控制策略取得了令人满意的结果。稳态调速指标小于3%，满足2 级精度指标要求；瞬时调速率指标远小于5%，满足1 级精度指标要求；稳定时间小于3 s，满足2 级精度指标要求。