湿式双离合器拖曳力矩算法及其应用
刘 波 张新桂 石兴磊 余子林 钟振远 李 佳
广州汽车集团股份有限公司汽车工程研究院,广州,511434
0 引言
汽车的动力性、经济性、换挡舒适性、效率和NVH(noise,vibration,harshness)等五大方面都和离合器有密切关系,虽然将来电动汽车(electric vehicle,EV)的推广趋势不可避免,但是离合器技术依然在MT(manual transmission)、AT(automatic transmission)、CVT(continuously variable transmission)、HEV(hybrid electric vehicle)、PHEV(plug in hybrid electric vehicle)等车型上发挥重要作用。湿式多片离合器作为车辆传动的核心零部件之一,决定着传动装置的可靠性以及使用寿命。准确计算和标定湿式离合器从分离到接合过程中拖曳力矩的变化过程,对改善车辆驾驶的舒适性、节省油耗等具有重要意义。
由于湿式双离合器的摩擦副之间有润滑和冷却油液,当主动端和被动端存在速差时,油液的剪切作用会产生拖曳转矩,引起功率损失、效率降低,同时还引起润滑油温升,因此减小拖曳功率损失是提高传动装置传动效率的关键。
目前,国内外很多学者针对湿式双离合器的拖曳力矩进行了大量的研究和试验。KITABAYASHI等[1]基于摩擦片和钢片间隙油液对流方式为层流的观点,提出了拖曳力矩的计算模型。该模型没有考虑相对转速较高时润滑油中出现的气穴现象,只适用于转速较低的拖曳力矩的预测,由于气穴油膜的剪切扭矩没有考虑,所以结果不精确。KATO等[2]在此基础上考虑了气穴的影响,弥补了该模型的缺陷,尽管得到的拖曳力矩公式与润滑油膜中气穴现象是从摩擦副的外径向内径扩张这一实际现象相悖,但仍为后续研究人员打开了思路。刘小川等[3]、杨李辰[4]、陈漫等[5]根据N-S方程建立了湿式双离合器拖曳力矩数学模型,揭示了润滑油的离心惯性作用是油膜收缩的原因,并根据润滑油表面张力计算出油膜的等效外径。项昌乐等[6]推导出了分离状态湿式双离合器润滑油膜雷诺方程,通过数值求解获取不同半径处的润滑油流量,根据实际供油量确定等效外径,最后利用牛顿内摩擦定理计算离合器拖曳力矩。马彪等[7]改进项昌乐的模型,建立了考虑表面张力和润滑油膜径向压力分布的方程,研究了表面张力、离合器不平行度对湿式双离合器拖曳力矩的影响。
学者们对拖曳力矩进行了大量试验研究。IQBAL 等[8]和HU等[9]通过试验验证了高速工况下油膜收缩现象,确定了离合器摩擦片槽型、槽深、对偶钢片与摩擦片间隙以及其中润滑油流速的影响规律,并指出了增大摩擦片波纹度可以有效减小拖曳力矩,然而波纹度对离合器拖曳力矩影响的理论研究少有学者涉及。
本文研究了低速阶段汽液两相流拖曳力矩的变化规律和计算方法并进行了验证,得到了当量半径、峰值力矩、临界转速之间的关系。
1 湿式双离合器工作原理
图1为某湿式双离合器的构造、冷却润滑示意图,外侧为控制奇数挡位离合器K1,内侧为控制偶数挡位离合器K2,K1接合和K2分离时,动力由输入轴输入,经过K1外毂传至K1钢片,再通过K1摩擦片传至内毂,由输出轴1输出,此工况下,K1的控制油压压紧蝶形弹簧使摩擦片接合,K2回油使得回位弹簧回位,K2分离。同样K1分离和K2接合时,动力由输入轴输入,经K2外毂传至K2钢片,再通过K2摩擦片传至内毂,由输出轴2输出,此时K2的控制油压压紧回位弹簧使摩擦片接合,K1回油使蝶形弹簧回位,K1分离。

图1 某湿式双离合器构造冷却润滑示意图
为保持离合器性能正常,必须使用润滑冷却油来维持其良好的散热和润滑。冷却油由专用油道进入,通过油腔进入K2摩擦副,并通过K2外毂圆周面上的出油口进入K1摩擦副,通过K1外毂流出至变速箱壳底,DCT结构设计中,K1和K2共用冷却润滑的设计较为普遍。
2 拖曳力矩的分析和计算
2.1 拖曳力矩的力学过程
彭增雄[10]将拖曳力矩的力学过程分为五个阶段,如图2所示,描述了离合器摩擦副间隙中的拖曳力矩力学过程。

图2 拖曳力矩和转速差示意图
(1)第一阶段(流体黏性摩擦)为单相流体阶段,即对全油膜覆盖状态流体的黏性剪切力的描述。
(2)第二阶段(流体黏性摩擦)为两相流体阶段,即对全油膜覆盖和气穴油膜覆盖状态的黏性剪切力的描述。
(3)第三阶段(该阶段以上为碰撞摩擦)为两相油膜和结构体相互运动状态,即对两相油膜黏性剪切力和微滑摩力矩的描述。
(4)第四阶段为两相油膜和非线性振动响应阶段,即对两相油膜黏性剪切力和滑摩力矩的描述。
(5)第五阶段为两相油膜和摩擦片,蝶形弹簧(或回位弹簧)柔性体的结构颤振现象。
假设输出转速为0,输入转速随时间增大,以转速差Δω为输入转速。在第一阶段,输入转速增大,拖曳力矩Tdrag随之增大,此时摩擦副间隙为全油膜,且流体对流方式按层流考虑,达到某一转速时Tdrag达到某一峰值B(即临界点),也就是全油膜和气穴油膜的分界点。B点对应的力矩即峰值力矩,B点对应的转速为临界转速。过了B点后,由于油膜具有表面张力,油膜开始从摩擦片外径向内径收缩,此时空气进入,气穴油膜产生,由于全油膜的剪切面积缩小,气穴油膜剪切面积增大,气穴油膜黏性力远远小于全油膜黏性力,所以Tdrag逐渐减小。到达C点后,全油膜理论上缩至摩擦片内径,但是由于油膜和摩擦片具有黏着力,此时仍然有一部分全油膜覆盖在摩擦片上,气穴油膜虽在此时剪切面积达到最大,但是由于其黏性力小得多,所以Tdrag达到最小值。过C点后,转速进一步增大,此时摩擦片和钢片开始局部接触碰撞,故C点可以理解为KP开始点(kiss start-point),转速进一步增加,此时摩擦副间隙中流体Tdrag变为次要力矩,滑摩力矩为主要力矩,由于Tdrag比滑摩力矩要小得多,所以此时Tdrag缓慢增大。到达D点时,可以理解为摩擦片紧贴钢片,输入和输出转速同步,过D点后表现为非线性颤振,扭矩突然上升至E点,此过程Tdrag称为带排转矩,此阶段有可能导致离合器热损坏,即烧片。D点可以理解为KP终点(kiss final-point)。从E点到达F点时,由于高速导致摩擦片产生结构颤振,带排转矩继续增大,过E点后应该考虑摩擦片、回位弹簧的柔性变形来减小带排转矩。因此带排转矩由F点降至G点。本文针对第一、第二阶段展开研究,关注与Tdrag相关的因素。考虑到开发效率,本研究不涉及摩擦片的沟槽形状和第三到第五阶段的影响。
2.2 冷却润滑油膜的收缩特性
在研究Tdrag过程中,YUAN等[11]通过VOF方法,模拟了离合器工况、制动器工况下气液两相流的油膜和转速的关系,如图3摩擦副间隙中的油膜所示,油膜的特性之一是具有表面张力(收缩力)Fα,它随着输入转速的增加而增大,同时受到离心力Fω的作用。Fα的关系Fω如下:
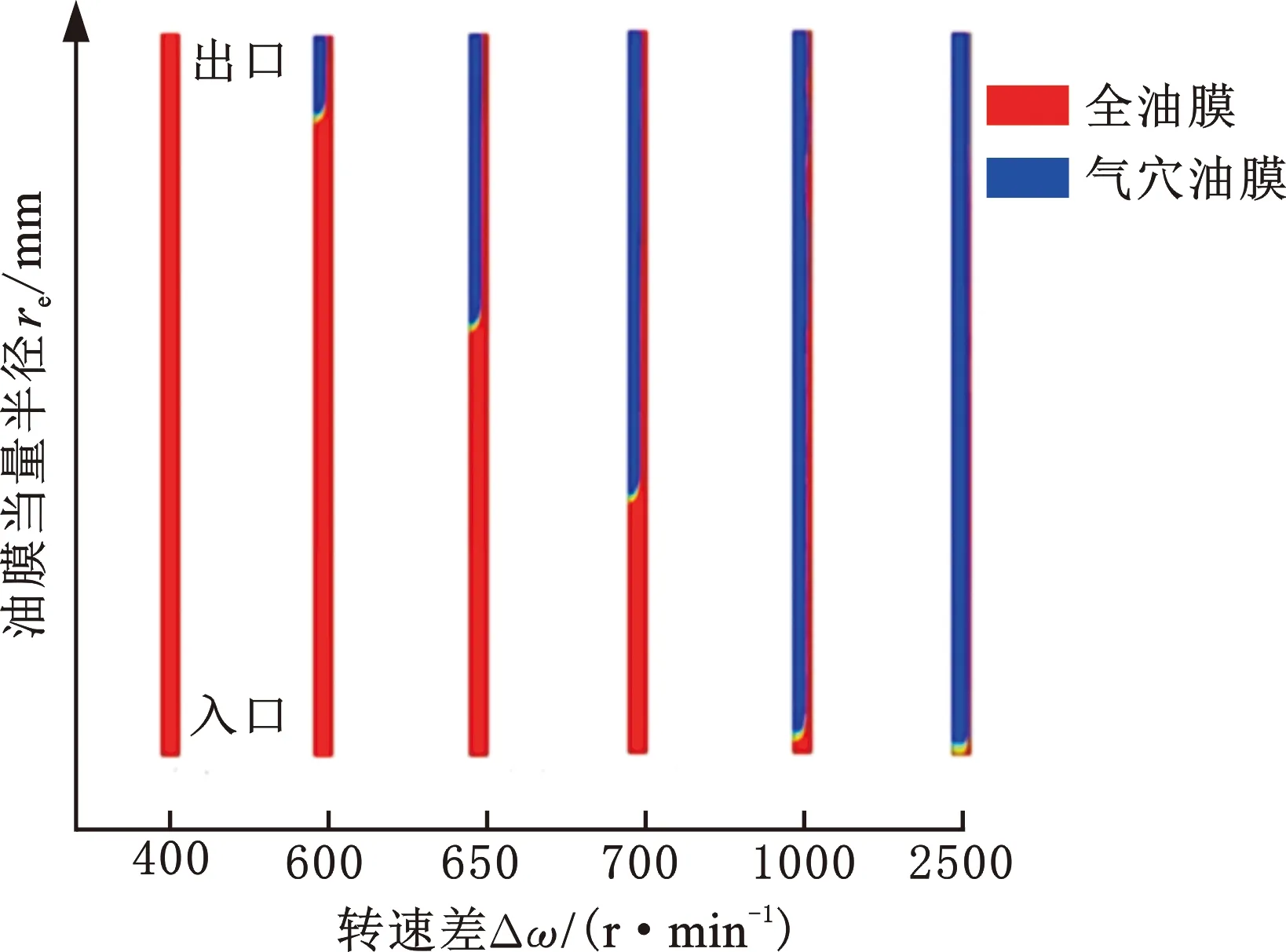
图3 润滑油膜和转速
(1)Fα>Fω时为全油膜覆盖润滑状态,当量半径re(即润滑半径)大于摩擦片外径ro。
(2)Fα=Fω时为临界润滑状态,当量半径re约等于摩擦片外径ro。
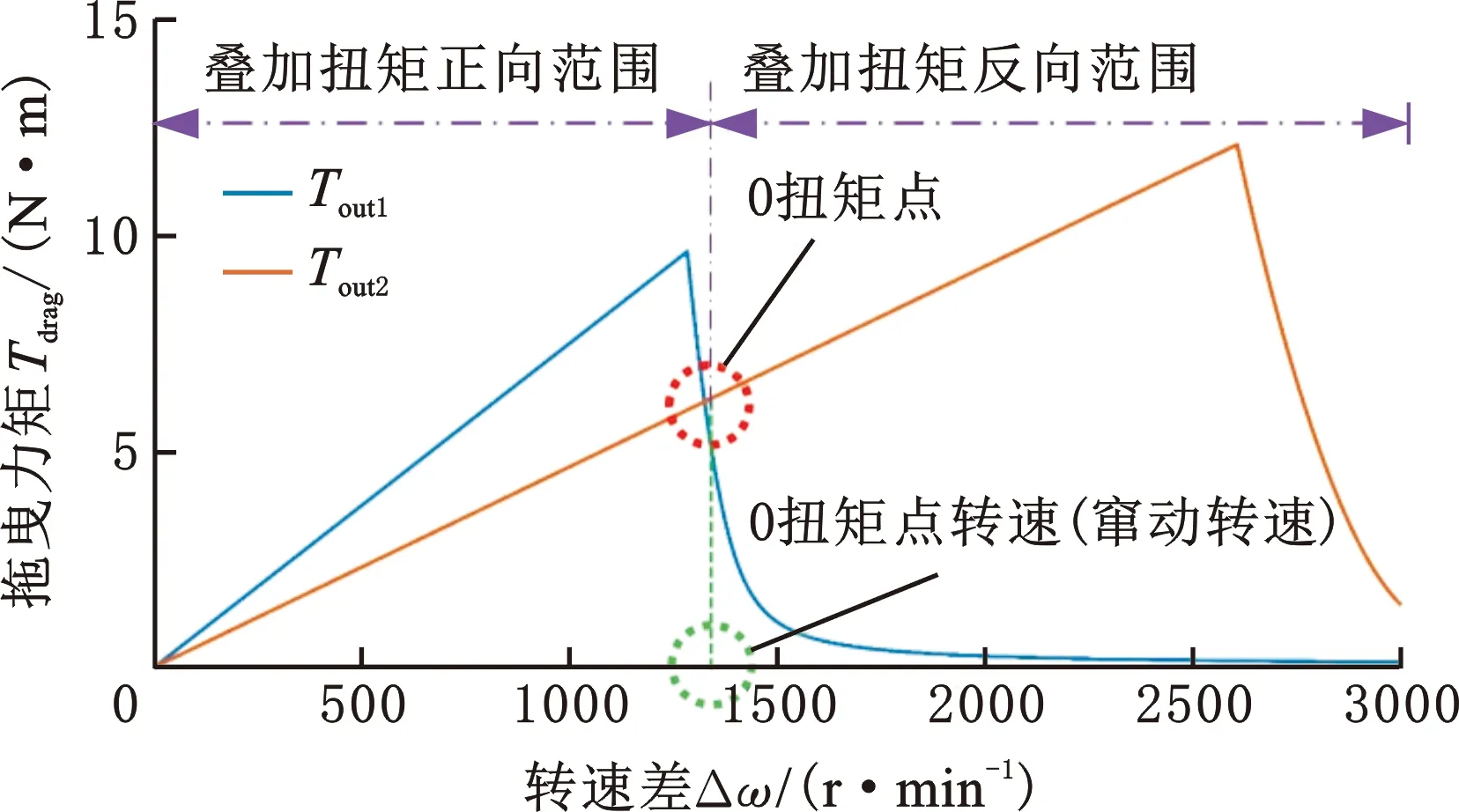
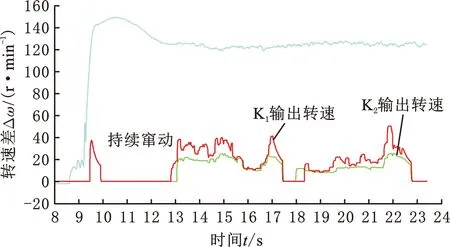
(3)Fα (4)Fα=Fαmin≪Fω时为气液两相润滑极限状态,当量半径re约等于摩擦片内径ri。 即便re≈ri时,摩擦片底部仍有一层全油膜的薄膜黏附,所以实际工况中re≠ri。 杨世铭等[12]的传热理论将流体运动分为层流、过渡区和湍流,如图4所示,横轴为油膜掠过长度,纵轴为油膜厚度。u为流速,从0开始,沿ux方向为主流速方向,垂直于主流方向的流速为uy,油膜厚度约为0.02 mm,黏性底层为油膜附着在摩擦片上的薄层。由于黏性油膜存在当量半径re,本文按照初始re≈ro考虑,油膜厚度远远小于掠过长度,因此流体速度从0开始到接近主流速度。由于摩擦片外径ro以外不再有钢片的支撑,可以认为摩擦片外径ro以内为层流,ro以外主要为湍流,层流和湍流之间有过渡区,ux和uy的变化都将是十分剧烈和不稳定的。因本文研究的是ro以内的区域,即层流,故暂不考虑ro以外的过渡区和湍流区域的影响。 图4 层流和湍流 2.4.1当量半径、单相流状态的拖曳力矩 本文针对第一、二阶段展开具体研究,即研究液态单相流和气液两相流拖曳力矩的计算方法,解析模型主要由流体力学N-S方程以及流体的连续性方程推导得到: (1) 式中,μ为油膜动力黏度;qV为润滑流量;h为摩擦副间隙;ρ为润滑油密度;ω为输入转速;α为表面张力系数;β为摩擦材料的接触角。 由于ω、μ、qV、h、ρ、α、β、ri这些参数均为已知数,可以计算出re。详细推导见文献[10,13]。 输入转速已知,可以计算出第一阶段单相流拖曳力矩: (2) 式中,n为摩擦面的面数。 2.4.2气液两相流状态混合动力黏度的计算 两相流混合区域内的平均含气量 (3) 式中,ω2为输出转速。 气穴油、空气、全油膜的密度ρH、ρG、ρL计算方法分别如下: ρH=ϑρG+(1-ϑ)ρL (4) (5) (6) 式中,qVG为空气流量;μG为空气动力黏度;x为两相混合区域内比例系数;μH为气穴油动力黏度,由式(3)~式(6)计算得到。 2.4.3气液两相流状态拖曳力矩的计算 气液两相流状态下的拖曳力矩可由流体力学的流体剪切应力的积分推出,如下所示: (7) 将式(1)求得的当量半径re、式(3)~式(6)求得的μH代入式(7),求得第二阶段的拖曳力矩T2,并与式(2)计算得到的T1相加,即可得到图2中第一阶段和第二阶段的拖曳力矩: Ttotal=T1+T2 (8) 综上所述,由式(1)可知,转速差的变化导致了油膜离心力的变化,离心力变化导致了油膜收缩变化,即导致了当量半径变化。图5所示离合器K1、K2当量半径中直线部分为摩擦片的外径,此时处于全油膜阶段,摩擦片外径等于当量半径。当转速差增至临界转速时,空气开始进入摩擦片间隙,处于临界状态,如转速差继续增大,油膜收缩加剧,当量半径按照式(1)递减。当量半径和转速差在变化过程中,拖曳力矩也同时变化,详见式(7)和图6。当量半径等于摩擦片外径时,拖曳力矩呈线性增大。这是因为该阶段为液体单相流阶段,转速差达到某一拐点时,拖曳力矩达到峰值力矩;随后,当量半径开始收缩变小,全油膜体积减小,气穴油膜体积增大,因此全油膜力矩减小,气穴油膜力矩增大,但气穴油膜黏度小于全油膜黏度,所以该阶段拖曳力矩仍然按式(7)减小,即当量半径开始收缩时拐点所对应的转速差等于拖曳力矩达到峰值力矩时的转速差(即临界转速)。由此可见临界转速和当量半径、峰值力矩存在一种相互影响的动态关系。 图5 K1、K2当量半径(θ=10 ℃,qV=1 L/min,h=1.7 mm) 图6 K1、K2拖曳力矩计算(θ=10 ℃,qV=1 L/min,h=1.7 mm) 表1所示为本文模型的基本参数。 表1 离合器K1、K2的计算参数(θ=10 ℃) 图5和图6所示为两个离合器的当量半径和拖曳力矩的计算结果,当转速差较小时,油膜离心力小于油膜表面张力,此时摩擦副间隙为全油膜覆盖状态,故当量半径为一直线,相应的拖曳力矩呈直线型递增,达到某一转速(即临界状态)时,对流方式处于层流和湍流的过渡区,因此拖曳力矩处于极不稳定的状态。离合器在设计时应该充分考虑到拖曳力矩所对应的转速(即临界转速)。随着转速进一步增大,油膜表面张力小于离心力,油膜向内径收缩,因此全油膜面积减小,气穴油膜面积所占比例增大,但是气穴油膜黏度远小于全油膜黏度,因此临界点过后,拖曳力矩是减小的,仿真结果与前述理论分析结果相符。 从式(1)和式(7)分析,影响拖曳力矩的主要因素为流量qV,qV增大,Ttotal将增大,反之减小;摩擦副结构间隙h减小,Ttotal将增大,反之减小;温度越低,油液动力黏度越大,导致Ttotal增大,反之减小。以下的例子以qV为1、5、10 L/min,油温θ为-10、0、10 ℃,间隙h为1.7、2.2、2.7 mm来分析,分析对象为离合器为K1。图7~图9的仿真结果揭示了影响拖曳力矩的关键因素:①流量增大则扭矩增大,反之则减小;②温度升高则扭矩减小,反之则增大;③摩擦副间隙减小则扭矩增大,反之则减小。 图7 拖曳力矩不同流量下的仿真结果(θ=10 ℃,h=1.7 mm) 图8 拖曳力矩不同温度下的仿真结果(qV=1 L/min,h=1.7 mm) 图9 拖曳力矩不同间隙下的仿真结果(qV=1 L/min,θ=10 ℃) 图10和图11所示为K1和K2两个离合器在相同工况下,实测数据与仿真数据的结果,对比分析发现: 图10 K1拖曳力矩不同流量下的的仿真和实测结果(θ=20 ℃) 图11 K2拖曳力矩不同流量下的仿真和实测结果(θ=20 ℃) (1)同工况下,两个离合器拖曳力矩均随转速增大而递增,过了峰值转速以后的气液两相流阶段拖曳力矩是减小的,且K2的峰值力矩和临界转速要大于K1的相应值,随着流量的增大而增大,实测结果和图2、图6的理论分析相吻合。 (2)导致误差的因素:在测试一个离合器时,仅仅拆除另一个离合器摩擦片和钢片,而输出轴、密封端盖、内外毂等是保留的,这些都将影响拖曳力矩,而数学模型未将其考虑在内;变速箱台架测试时输入转速每增加500 r/min采集拖曳力矩,采样点不足;本次研究没有考虑摩擦片的沟槽形状,沟槽形状也是拖曳力矩的重要影响因素之一;高转速将导致摩擦片颤振产生扭矩突升,此处未研究。 (3)结果虽然有误差,但两个离合器的仿真和测试结果的趋势基本一致,和实测较为符合。 笔者所在企业在开发一款湿式DCT时,在整车测试试验中发现,冷启动车辆时N挡或P挡怠速,电子驻车未解除,整车怠速起始阶段经常出现轻微前后窜动感觉,怠速转速稳定后,状况消失,早上启车怠速,发生频率大概50%左右。笔者上车测试发现车身窜动感明显,如图12所示,转速波动越密集,车身窜动越明显。测试工况为油温20 ℃,流量1 L/min,转速1200 r/min,经过改变流量、改变油温等多轮工况测试,发现: 图12 实车测试窜动 (1)油温-20~10 ℃时,车身窜动频繁,故窜动和温度相关。 (2)窜动仅在1200 r/min时发生,故窜动和转速相关。 (3)窜动在输入转速1200 r/min左右时发生较大波动,故推断窜动和转速波动相关。 N挡、P挡时两个离合器是分离状态,除了拖曳力矩没有机械动力输出,因此初步断定和离合器的拖曳力矩有必然的联系。前述内容笔者阐明了拖曳力矩的变化规律,临界转速和峰值扭矩的关系,以下分析K1和K2拖曳力矩的传递特性。 如图13所示,K1的拖曳力矩Ttotal1经过内输入轴,通过一个挡位齿轮传递至差速器(车轮端): 图13 K1、K2拖曳力矩传递路径 Tout1=Tdrag1in (9) K2的拖曳力矩Ttotal2经过外输入轴、一个挡位齿轮和倒挡R挡位齿轮传至差速器(车轮端): Tout2=-Tdrag2iR (10) iR=0.77in (11) 其中,Tout1为Tdrag1输出到差速器的扭矩,可以理解为前进方向的力矩;Tout2为Tdrag2输出到差速器的扭矩,可以理解为倒退方向的力矩,Tout2和Tout1方向相反;in为Tdrag1经过1挡至差速器的速比;iR为Tdrag2经过R挡预挂至差速器的速比。两个离合器同传至差速器,这里只需要比较传至差速器的拖曳力矩,因此in可考虑为1。根据牛顿第一运动定律,两个方向相反的力矩在某一力矩点相交,会出现正负力矩交替输出,又由于拖曳力矩本身就属于波动力矩,因此在该交点处将会出现扭矩波动现象。目前判定是这种波动现象导致了车身窜动,将该力矩点称为0扭矩点,对应的转速称为0点转速。由式(9)~式(11)可以计算Tout1和Tout2。 图14所示为拖曳力矩传至差速器端的力矩的计算结果,本文所测试的两个离合器和前述测试离合器均为同一款两个离合器。从图中可以看出,K1传至差速器的拖曳力矩Tout1和K2传至差速器的拖曳力矩Tout2存在0扭矩点,其对应转速为1320 r/min,该工况实测窜动时怠速转速为1200 r/min(与仿真结果的误差率为10%),因此只要怠速转速避开1200 r/min(仿真1320 r/min),即可改善车身窜动状态。前述论证说明,改变油温、改变流量、改变间隙会改变0点扭矩和转速,根据整车的实际情况,通过预充离合器的油压可以达到减小离合器间隙的目的。本次整车怠速工况测试为K1油压保持不变,预充K2油压,油压值为KP点的油压(离合器接合时的控制油压)-0.02 MPa,实际预充油压为0.33 MPa,图15和图16所示为本次实车测试的结果。 图14 拖曳力矩在怠速工况、0扭矩点的仿真结果(θ=10 ℃,qV=1 L/min,h=1.7 mm) 图15 充油前实车测试结果 图16 充油后实车测试结果 由图15、图16对比可知,预充油压是有效的策略之一,同时也证明了只要计算出0点扭矩所对应的0点转速,通过调整离合器0点转速来避开发动机的怠速转速,就可能避开车身窜动的现象。 表2示出了-20~20 ℃的仿真参考值,如需考虑增大流量、提高温度,只需改变相应参数即可得到对应结果。 表2 仿真参考值 综上所述,本次车身窜动是因为离合器本身具有临界转速和峰值力矩,此处润滑油膜处于不稳定的临界波动状态;由于两个离合器输出的拖曳力矩一正一反,必然存在一个0点扭矩所对应的0点转速,正是这个0点转速导致了车身窜动,故可通过调整该0点转速改善怠速工况车身窜动。 本文研究了低速阶段气液两相流拖曳力矩的变化规律以及计算方法,通过仿真和测试数据对比,验证了该研究结果的有效性,提出了临界转速的边界特性,揭示了油膜当量半径、临界转速、峰值扭矩三者相互影响的动态关系。在某款湿式双离合器的开发中,首次提出了0点扭矩以及0点转速的概念,为改善车身窜动提供了策略,为进一步研究离合器的滑摩性能提供了参考。但是本研究仅针对无沟槽的摩擦片进行分析,而实际的摩擦片通常都带有各种形状的沟槽,因此今后将继续研究带沟槽的摩擦片的离合器滑摩特性,以及中高速离合器带排转矩(即第三、第四、第五阶段)的变化规律和特性。2.3 层流和湍流
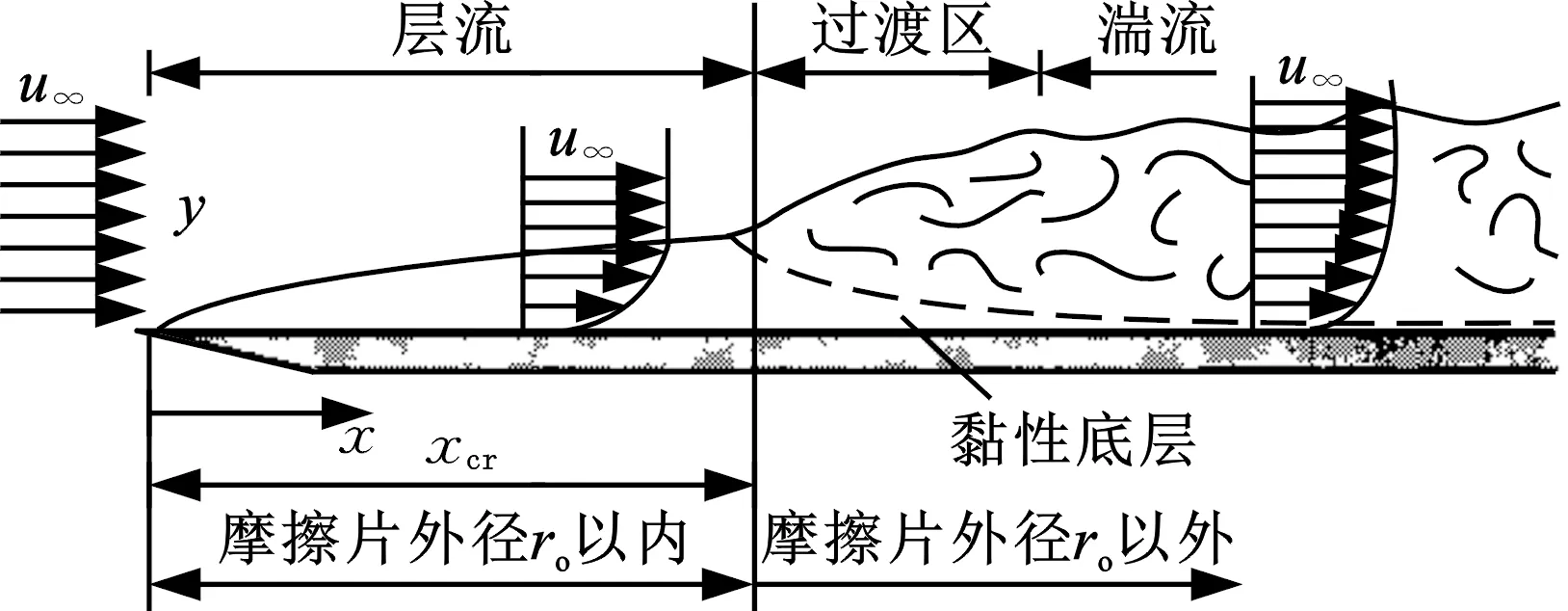
2.4 第一、二阶段拖曳力矩的计算



3 拖曳力矩的影响因素
3.1 仿真计算

3.2 拖曳力矩影响因素
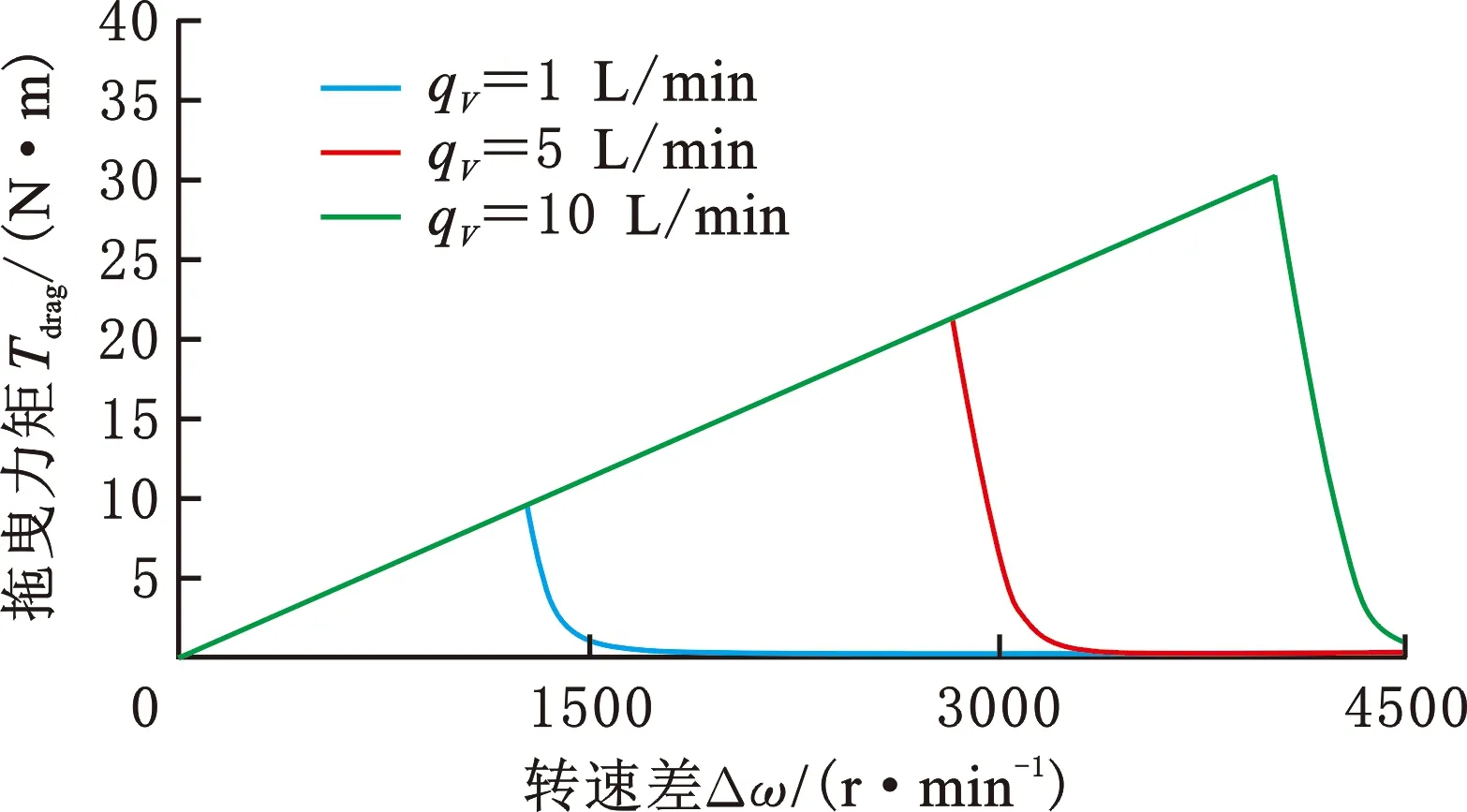

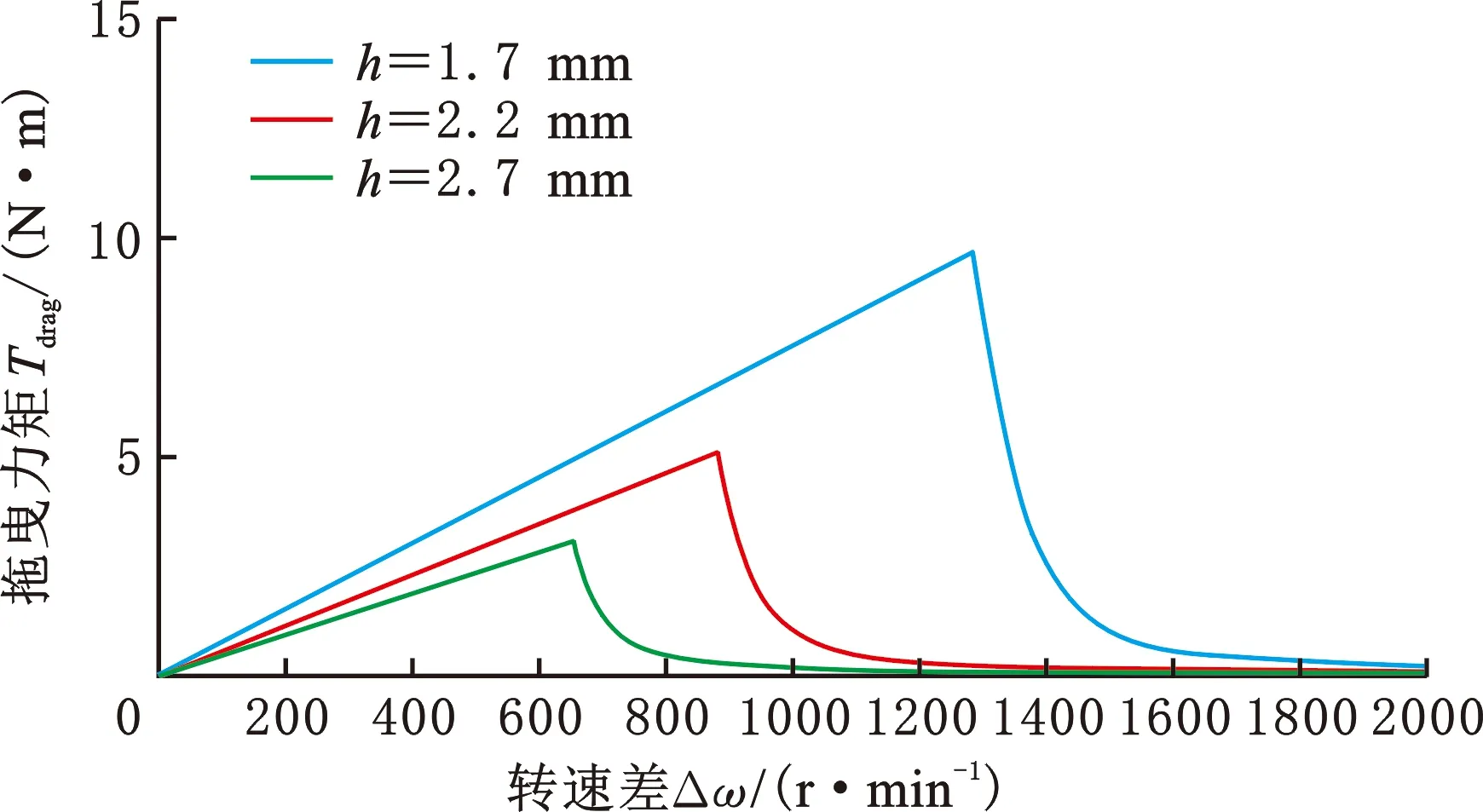


4 拖曳力矩算法的应用性
4.1 机理分析


4.2 仿真和实车测试的对比


5 结论

