反应堆压力容器下封头热蠕变模型的开发及在OLHF实验分析中的应用

杨 皓 张 斌,2 高鹏程 唐绍伟 单建强,2

1（西安交通大学能源与动力工程学院 西安710049）

2（西安交通大学动力工程多相流国家重点实验室 西安710049）

如果发生导致压水堆（Pressurized Water Reactor，PWR）堆芯熔毁的严重事故，大量熔融物可能会重新定位到反应堆压力容器（Reactor Pressure Vessel，RPV）下封头的底部［1］，并产生局部加热。这种情况可能导致下封头发生破裂失效，导致大量具有极大放射性的堆芯材料释放到安全壳甚至环境中去。为了避免发生放射性大量释放到环境的严重事故，我国的第三代压水堆（如HPR1000）以及随后的新型设计中均使用了熔融物堆内滞留（In-Vessel Retention，IVR）策略［2］。RPV 下封头在IVR 策略中具有十分重要的作用，合理有效地评估下封头在高温环境中的蠕变行为具有重要意义。

自从切尔诺贝利事故发生以来，世界各国开展了许多下封头失效的缩比实验以及相应的数值模拟研究。其中包括LHF（Lower Head Failure）实验［3］、OLHF（OECD Lower Head Failure）实验［4］等。其中，在USNRC（U.S.Nuclear Regulatory Commission）/SNL（Sandia National Laboratories）下封头失效项目下进行的LHF 实验，旨在研究下封头在高压（大多数情况下为10 MPa）和小贯穿温差下的行为。另一个USNRC/SNL 下封头失效项目称为OLHF 实验，是在经济合作与发展组织（Organization for Economic Co-operation and Development，OECD）的一个项目框架内进行的。OLHF实验是LHF实验的扩展，研究中低压（2～5 MPa），但有较大的贯穿温度情况下下封头失效行为。这些实验能够更好地理解RPV 下封头的机械行为，这在严重事故评估和事故缓解策略中十分重要。由于进行真实的下封头失效实验十分昂贵且具有很大的风险性，更多的研究人员根据目前已有的实验数据进行了相应的数值模拟［5］。目前主要的严重事故分析程序有：MAAP［6］、ASTEC［7］以及MELCOR［8］等，包括西安交通大学自主开发的一体化严重事故分析程序ISAA［9］都是采用的十分简单的下封头失效模型。目前针对下封头在严重事故中的完整性研究，许多局限于熔融物对壁面的烧蚀作用，比如仅考虑达到下封头材料熔点以判断失效［10］，而未综合考虑事故工况下下封头所受复杂温度、应力场的共同作用。这些系统性程序在进行计算时存在准确度低的问题，因此开发一种简单且准确度高的模型以弥补系统性分析程序的不足是很有必要的。

本文应用薄壳理论以及蠕变本构关系开发了用于分析下封头热蠕变行为的LHTCM 模型，以用于分析RPV下封头的蠕变失效。使用LHTCM模型对OLHF 实验进行了建模计算，通过数据的对比分析验证了模型有效性和正确性。结果表明：本文所开发的LHTCM模型可以弥补现有严重事故分析程序模型简单、准确度低的不足，可用来耦合到一体化分析程序对RPV的热蠕变行为进行分析。此外，RPV的失效时间、模式和位置等信息可以根据各种失效准则进行综合评估，提高了模型判断的准确性和可靠性。

1 LHTCM模型

1.1 概述

LHTCM 是一个旨在集成到一体化严重事故分析程序中计算下封头热蠕变失效行为的模块。LHTCM 模块为处于高温高压环境下的下封头提供了一个简单但有效的模型，能够分析下封头在该情况下的完整性以及预测其失效时间等。LHTCM 代码的计算流程图如图1 所示。首先是数据初始化，并输入下封头的壁温、内压以及几何尺寸等相关参数。之后分别对下封头节点的径向以及轴向应力进行计算，并计算等效应力。在本模型中使用Chu等［11］的实验数据对节点的蠕变应变进行计算。并通过失效准则的计算对下封头节点的完整性进行综合评估，最终给出下封头失效时间、破口位置等信息。

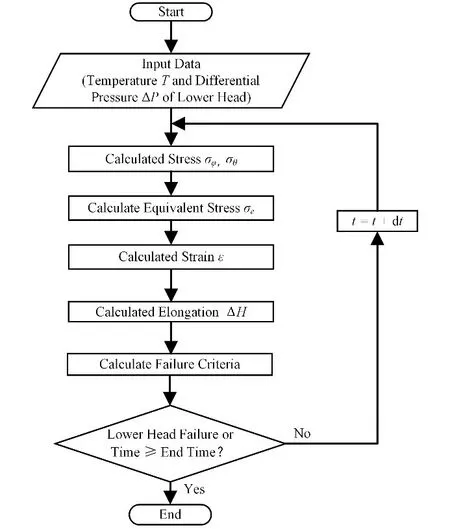
图1 计算流程图Fig.1 Calculation flow chart

1.2 力学模型

本文将下封头始终视为一个半球形结构，并假设在高温高压的环境中，下封头总是发生球形形变。通常情况下，下封头微元体的受力情况可由图2 表示，包括轴向应力Nφ、环向应力Nθ、剪切力Q、弯矩M等。一般只承受气体压力和静压力时，在壳体的大部分区域，其弯矩M、横向剪切力Q与薄膜内力相比是很小的［12］，如果略去不计，将使壳体的应力分析大大简化而不致引起大的误差。因此下封头微元体的受力分析可以简化为图3所示。

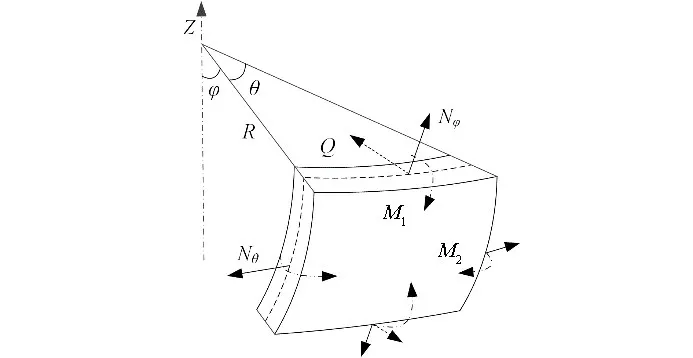
图2 下封头节点受力分析Fig.2 Stress analysis of lower head nodes

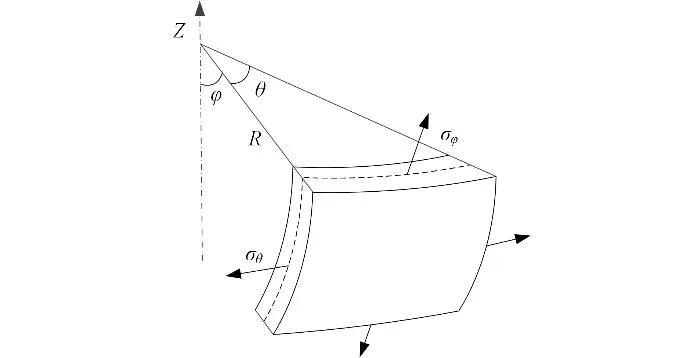
图3 简化后的受力分析Fig.3 Simplified stress analysis

在此假设情况下，下封头的应力可以使用球形容器薄膜应力的计算关系式。同时考虑到下封头以及内部熔融物的重力，轴向应力σφ以及环向应力σθ可由下式计算：

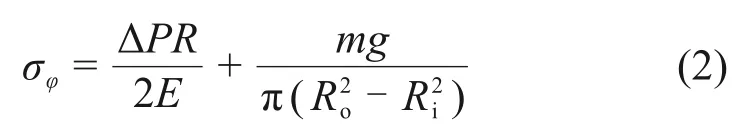
式中：ΔP为内外压差，MPa；E为壁厚，m；R为下封头计算节点的半径，m；Ro为下封头外半径，m；Ri为下封头内半径，m；mg为该受力截面以下部分的下封头自重以及内部熔融物的重力，N。

RPV材料的蠕变应变通过节点的等效应力计算而来，通过节点的受力分析Von Mises等效应力的计算关系式［13］见式（3）。

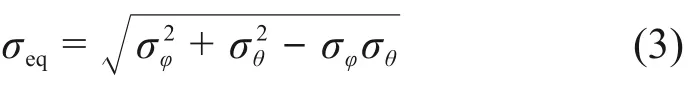
严重事故下的RPV 内壁会持续经受500 ～1 500 K高温［14］，并且高温承压容器和构件的主要失效形式是过度变形和断裂，即蠕变是下封头失效的主要因素［15］。本模型中的蠕变使用由SNL［11］通过实验拟合的公式计算。

式中：dε为应变增量；C（T）、m（T）为温度相关参数；σeq为等效应力，MPa；dt为时间增量（计算的时间步长），s。

因此节点的应变可由时步累加获得：

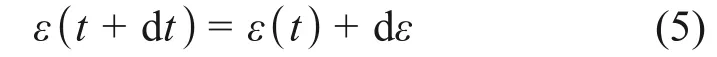
式中：ε（t）为t时刻的等效应变。

在计算时始终认为下封头为球形变形，因此下封头的高温蠕变伸长量由图4 表示。通过LHTCM模型计算得到的下封头节点等效应变进行几何转换，从而得到高温蠕变后最低点的伸长量。具体计算如下所示：

图4 下封头垂直伸长量Fig.4 Vertical elongation of lower head

在ISAA 建模中将下封头划分为M段，对应此时刻的应变值ε（IR）由LHTCM 模型计算得到。通过图4可知，经过高温蠕变后第IR段的垂直长度Δh（IR）由下式计算：

式中：Δh（IR）为第IR段的垂直长度，m(IR)为当前时刻第IR段的平均等效应变；Ro为下封头外半径，m；θ（IR+1）和θ（IR）为第IR段的两个截面角度，rad。

因此整个下封头的垂直伸长量ΔH应为：

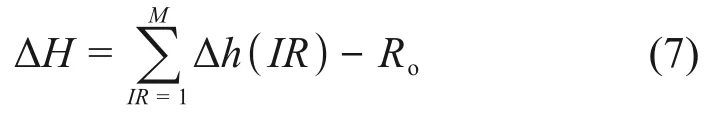
1.3 失效准则

ISAA 原有的失效判断模型认为下封头节点应变值达到18%即发生失效，这种使用经验参数的单一失效准则偶然性大、可信度低。而LHTCM 模型引入了4种失效准则，在计算过程中，这些准则都对下封头进行了完整性评估。每个失效准则都提供了下封头失效时间、对应的最底部伸长量以及破口位置等信息。同时根据模拟结果与实验数据的匹配度可以对几种失效准则进行准确性与适应性评估，通过结果的对比可以挑选出最佳判断准则。

1）高温熔点失效。当RPV 温度超过材料的熔点时（SA533B不锈钢熔点：1 810.15 K），下封头将由于高温熔化失效。

2）应变极限失效。作为参与OLHF实验项目基准测试的机构，GRS（Gesellschaft für Anlagen- und Reaktorsicherheit）和VTT（Technical Research Centre of Finland）等［6］分别以应变极限为20%和30%作为判断下封头失效的标准。在本模型中采用与之类似的准则即εfail=30% 进行下封头的评估，从而将LHTCM的计算结果与之进行对比分析。

3）Larson-Miller 失 效 准 则。Larson-Miller 准则［16］通过估计失效时间tr，并使用当前时间与tr之比表示失效份额D。当D达到1.0时下封头失效，公式如下：

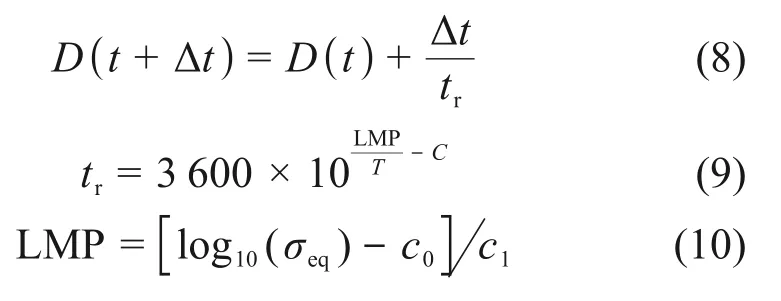
式中：D（t）为t时刻的损伤参数；Δt为计算的时间步长，s；tr为失效时间，s；T为下封头温度，K；LMP 为Larson-Miller参数；σeq为等效应力，MPa；C=20，与材料相关的常数；对于SA533B 不锈钢，c0=4.502，c1=-1.348×10-4。

4）Kachanov 蠕变损伤准则。下封头由于高温蠕变造成的损伤遵循Kachanov 提出的蠕变损伤准则［17］，计算关系式如下所示：

式中：D(t)为t时刻的损伤份额；为t时刻的损伤份额变化率，s-1；Ak为温度相关的材料参数；k，B与材料和温度相关详见参考文献［17］。

2 OLHF 实验模拟

2.1 实验简介

OLHF 实验项目是LHF 实验的延伸，都是在桑迪亚实验室进行的五分之一规模的实验［18］。OLHF计划是为了研究堆芯融毁严重事故下反应堆压力容器下封头失效的时间、模式和尺寸而组织的实验计划。其中OLHF-1 和OLHF-2 是在此计划框架下进行的两项实验。

OLHF-1 实验旨在研究1∶4.85 比例的反应堆压力容器模型在中等RCS（Reactor Cooling System）压力（5 MPa）下的蠕变破坏行为，该压力容器贯穿壁温差ΔTW达到150 K 或以上。实验装置顶部由一个空白法兰形成封闭环境。下封头上部圆柱部分高0.460 m，内径为0.914 m，标称设计壁面厚度为0.074 m，标称试验压力为12 MPa［19］。实验装置简化图如图5所示。

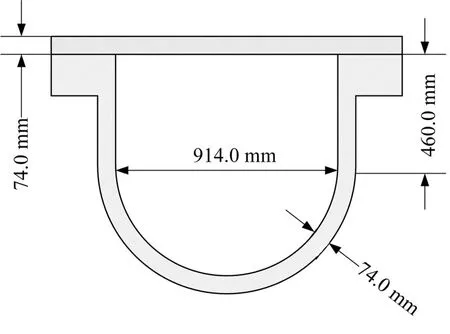
图5 OLHF实验装置示意图Fig.5 Diagram of OLHF experimental device

OLHF-2实验装置与OLHF-1相同，不过OLHF-1 实验研究的是下封头在中等RCS 压力（5 MPa）下的蠕变破坏行为，而OLHF-2 研究的为低RCS 压力（2 MPa）下的蠕变行为。

实验装置内部压力通过充入氩气控制，由初始充压开始逐步增压；容器内部温度的控制通过一个最高为750 kW 的加热器加热石墨线圈辐射加热实现。

2.2 数值建模

使用自主开发的严重事故分析代码ISAA 对OLHF 的两个实验进行数值建模，建模参数主要来自OECD 下封头失效实验最终报告中提供的数据［11］。OLHF实验装置的节点划分如图6所示。

图6 OLHF实验的数值模型Fig.6 Numerical model of OLHF experiment

其中，控制体CV001 为大气环境，相比较于CV002 和CV003 来说体积非常大且内部参数恒定，温度始终为300 K，压力为0.1 MPa；CV002 是内径为0.914 m 的下封头，其初始条件为大气参数；CV003是内径为0.914 m、高度为0.46 m的压力容器圆柱段。在整个实验过程中，CV002 及CV003 内部充满了氩气。在控制体外部有HTW00311、HTW00301 以及HTW00201 分别与环境进行换热。在数值模型中，用堆芯碎片模拟加热器并通过调节衰变功率控制下封头的壁温，从而模拟实验的升温过程。

表1 为下封头的节点划分。下封头的底部为90°，水平位置为0°，在数值模型中沿下封头0°～90°方向划分为9个径向段，分别对应OLHF-1实验中热电偶的测量位置。在沿壁厚方向上划分11 个温度节点。

表1 下封头节点划分Table 1 Node division of lower head

2.3 实验过程与模拟

2.3.1 OLHF-1实验模拟

实验装置的初始环境为大气环境，内部压力为0.1 MPa，初始温度为300 K。在实验过程中利用下封头底部的内壁面温度为基准来控制加热，即图7数值模型中TLH111 节点的温度。温升的控制依靠数值模型中衰变热功率的调节，从而实现实验的温度变化，以下为实验的加热过程。

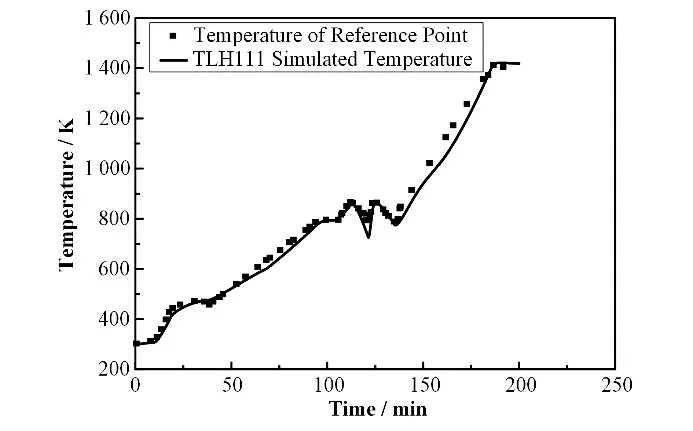
图7 OLHF-1下封头最底部内壁温模拟结果与参考结果Fig.7 Simulation results of inner wall temperature and reference point at the bottom of OLHF-1 lower head

首先经过一个初始启动瞬态，使下封头底部温度达到470 K，初始充压为2.5 MPa，由于加热的原因，压力增加到约4.0 MPa；

1）在470～800 K，使下封头底部的内部温度按6 K·min-1的加热速率加热容器至800 K，并且在加热之前不久（温度未高于500 K），容器充压至12.3 MPa；

2）96 min 后，容器的温度达到800 K，在此提供约10 min实验平台，在106 min结束；

3）106 min 之后，容器应该按照12 K·min-1的加热速率升温，但是由于电源出现故障，加热升温阶段在136 min重新开始。

通过图7可以看到，在初始瞬态阶段、6 K·min-1升温阶段、恒温平台阶段以及12 K·min-1阶段模拟计算的内外壁温与实验测量结果符合很好。实验过程中下封头内部的压力由ISAA 程序给定，从初始环境状态加热导致内压增加到约4.0 MPa，之后很快加压到12.3 MPa并基本维持不变，通过图8可以看到，模拟结果与实验过程一致。图9为下封头0°～90°范围内的内外壁温曲线，通过与实验测量数据进行对比，模拟的内外温差达到了实验要求的150 K 以上并与实验值符合得非常好。

图8 OLHF-1实验压力与模拟结果Fig.8 Simulation results of pressure and the OLHF-1 experimental pressure

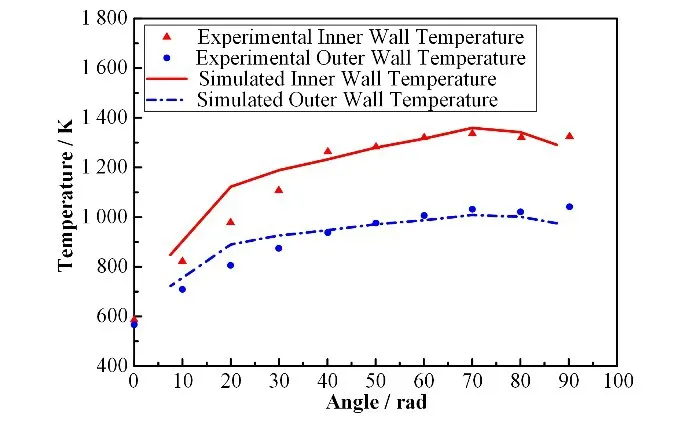
图9 180 min时OLHF-1实验内外壁面温度的分布Fig.9 Distribution of inner and outer wall temperature in OLHF-1 experiment at 180 min

2.3.2 OLHF-2实验模拟

OLHF-2 实验在5.29 MPa 的内部压力下进行，初始加热速率以6 K·min-1升高到800 K，然后在800 K 停留10 min，之后以12 K·min-1继续加热直到破裂。下封头在实验进行至213 min 时失效。测得的总垂直位移为17 cm（实时位移传感器测量为11.2 cm）。其中壁温和压力的模拟结果分别如图10和图11 所示，计算结果与实验测量结果基本一致，能够很好地复现OLHF-2实验过程。

图10 OLHF-2下封头最底部内外壁温模拟结果Fig.10 Simulation results of inner and outer wall temperature at the bottom of OLHF-2 lower head

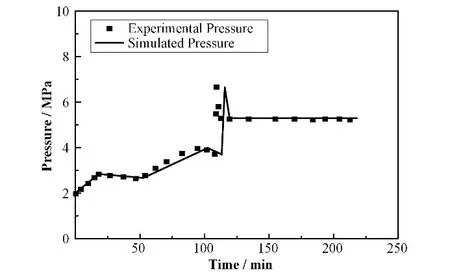
图11 OLHF-2实验压力与模拟结果Fig.11 OLHF-2 experimental pressure and the simulated results

为了展现对内外温差的模拟结果，将在190.0 min 时0°～90°的内外壁温与实验测量值进行了对比分析，如图12所示。通过对比可以看到与实验测量值符合良好，并且内外温差达到了实验预期的150 K以上。

图12 190 min时OLHF-2实验内外壁面温度的分布Fig.12 Distribution of inner and outer wall temperature in OLHF-2 experiment at 190 min

3 计算结果与分析

3.1 OLHF-1结果与分析

在OLHF 项目框架内，各研究机构都进行了相应的数值模拟［6］。本文把LHTCM 模型计算结果与实验数据以及其他参与者的结果进行了对比分析。

1）失效准则的分析

在LHTCM模型中总共使用了4种失效准则，通过多准则共同分析，避免了单一失效准则可靠性低的问题。各个准则计算结果为失效分数，并认为等于1.0 时节点失效。模拟OLHF-1 实验依据不同失效准则得到的失效时间、破口位置以及伸长量的结果如表2 所示。其中失效准则b、c 和d 都判断下封头已经发生了失效，准则a 没有达到失效标准。各个准则判断的下封头破口位置都在65°～75°，与实验位置基本一致。不同准则计算的失效时间等都不尽相同，其中准则c 各个计算结果都与实验数据符合最好，下文也以失效准则c的结果进行分析。

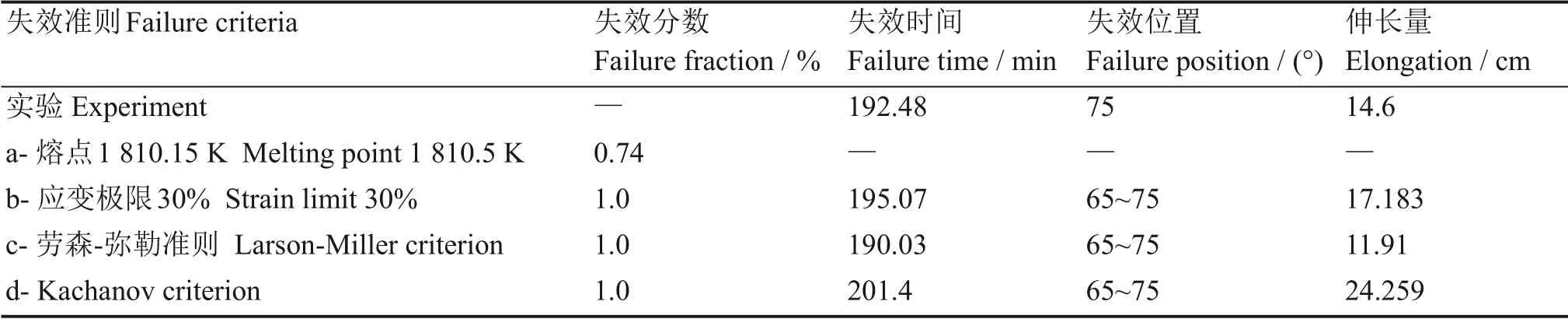
表2 各失效准则计算结果Table 2 Calculation results of each failure criterion

图13为下封头第三个轴向环即65°～75°范围内沿壁厚最外侧节点的失效准则随时间的变化曲线。

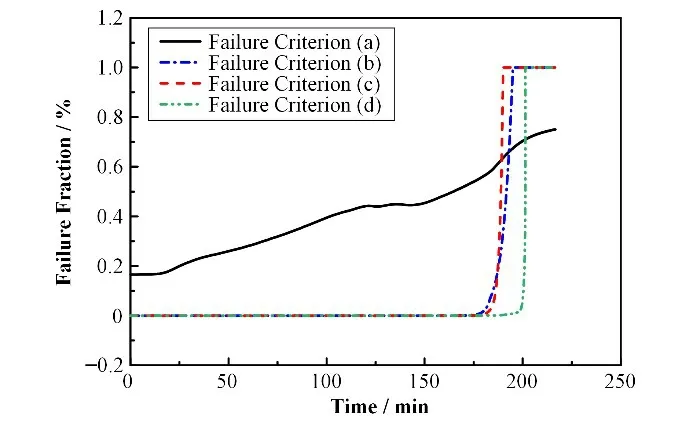
图13 失效准则变化曲线Fig.13 Variation curve of failure criterion

2）失效时间及位置

在OLHF 实验中，下封头失效时间以及破口位置是极其重要的信息。表3 总结出了LHTCM 与实验数据以及其他模型计算结果的比较。实验测得下封头失效的时间为192.48 min，破口位置为75°左右。使用原版的ISAA 程序计算的失效时间为184.5 min，与实际数据的相对偏差为4.1%；而使用改进后的LHTCM 模型所计算的失效时间为190.03 min，与实验记录的192.48 min相对误差仅有1.3%。其他机构开发的模型计算的失效时间也基本是偏早的，由于使用的失效准则较为单一且多为经验值作为判据，容易导致结果带有较大偶然性。由此可见LHTCM模型在计算时间的精度上有了较大的提高。在预测失效位置方面，模型计算结果处于65°～75°之间，相比较于实验的75°来说比较准确。总体来说，本文所开发的LHTCM 模型计算结果与实验数据十分符合，相比较于ISAA 原有的模型有了很好的改进。

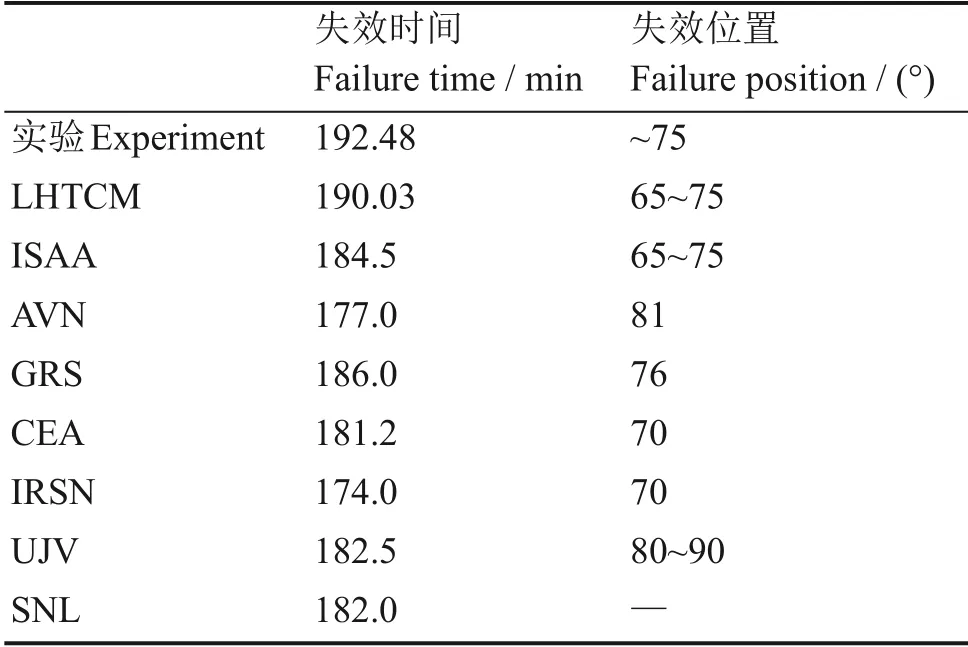
表3 结果对比Table 3 Comparison of results

3）底部伸长量

图14给出了LHTCM模型以及其他模型所计算的下封头最低点的伸长量变化。OLHF-1 实验最终失效时测得下封头垂直伸长量约为14.6 cm，对于大多数模型计算的垂直位移都小于实验值且时间都比较提前。ISAA 原本的模型认为失效应变最大为18%，由此计算得到的垂直伸长量仅有1.1 cm。本文所开发的LHTCM模型采用了多种失效准则进行比较分析，最终得到下封头失效时的伸长量为11.91 cm。通过与不同模型结果的对比分析可以看到LHTCM 模型能够更为准确地反映出OLHF-1 实验中的下封头伸长情况，相比较ISAA 原有模型更加准确。

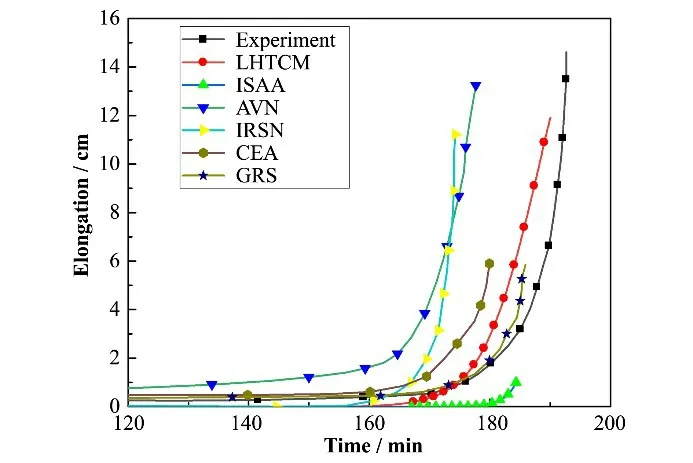
图14 下封头底部伸长量Fig.14 Elongation at bottom of lower head

3.2 OLHF-2结果与分析

1）失效准则的分析

与OLHF-1实验的模拟结果较为相似。其中失效准则c 和d 计算结果与实验相比较更为接近（表4），在失效位置上与实验结果有些偏差。在实验的末期即下封头失效前的十几分钟内所测得的温度有100～200 K 的波动（具体可见最终报告［11］），可能是在这个时间点下封头严重变形，温度较高的下封头底部材料大量融化从而导致靠近底部的40°范围内节点温度发生剧烈的变化。但是在数值模拟中并不能将这个过程复现，从而导致模拟失效位置与实验有一定的偏差。图15 为OLHF-2 失效分数的计算结果。

图15 失效准则变化曲线Fig.15 Variation curve of failure criterion

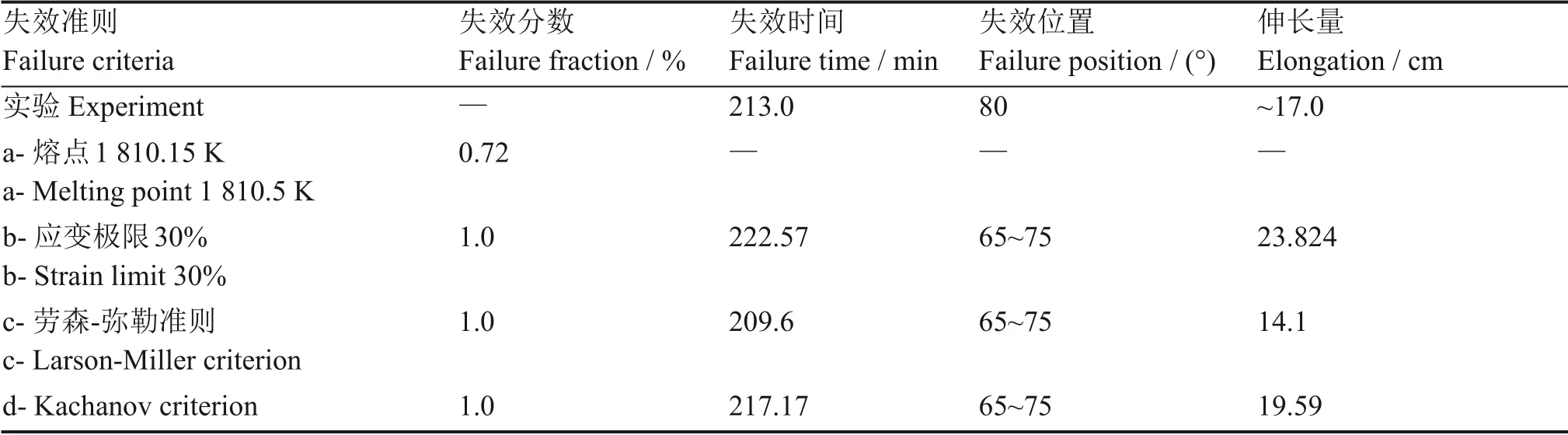
表4 各失效准则计算结果Table 4 Calculation results of each failure criterion

2）失效时间及位置

在此分析了LHTCM 以及原版ISAA 与实验结果的对比，如表5 所示。与实验数据相比，ISAA 计算的失效时间更加提前，误差为6.1%；而LHTCM误差仅有1.59%。

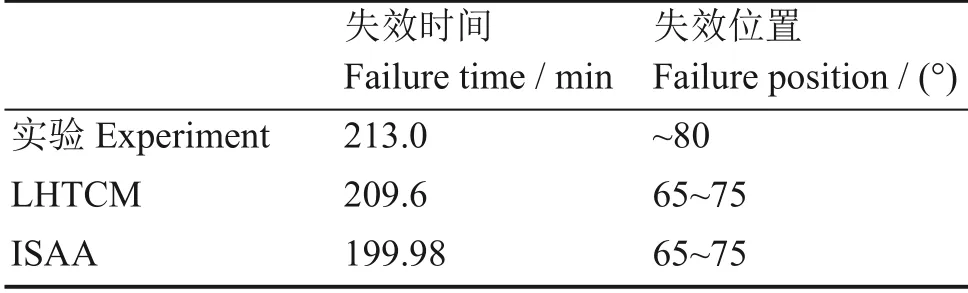
表5 失效时间及位置结果对比Table 5 Comparison of failure time and location results

3）底部伸长量

在OLHF-2 实验中，通过位移传感器的位移信号得到的位移曲线如图16所示，但是通过最终测量的下封头位置为约17 cm［11］。通过曲线可以明显看到LHTCM 模型的计算结果相比较原版的ISAA 具有很好的提高。

图16 下封头底部伸长量Fig.16 Elongation at bottom of lower head

4 结语

在发生反应堆堆芯熔化的严重事故时，大量熔融物重新定位到压力容器下封头内产生高温的恶劣换热环境。在长时间的高温作用下，下封头会发生严重的蠕变现象导致熔融物堆内滞留的严重事故缓解措施失败。为了能够对下封头的状态进行准确地评估，本文基于简化的薄壳理论以及蠕变方程开发了LHTCM 模型，并将LHTCM 模型应用于模拟OLHF 实验。通过计算结果与实验数据的对比分析，验证了LHTCM 模型的有效性和准确性。所得到的结论主要有以下几点：

1）LHTCM 模型计算得到的下封头失效时间、破口位置以及底部伸长量与实验数据符合较好，相比较于ISAA 的简单模型能够更好地对下封头进行有效评估；

2）下封头在高温环境长期作用下，导致其没有达到材料熔点便会由于蠕变发生失效；

3）在本文中使用的几个失效准则中，Larson-Miller失效准则能够更为准确地做出下封头失效的判断。

因此，本文所开发的LHTCM 模型能够有效地模拟RPV 的失效时间、破口位置等重要信息，相比较严重事故分析程序ISAA 的简单模型更加准确，并且弥补了判断下封头失效准则的单一、可靠性不高的缺点。

同时，针对LHTCM模型提出以下几点展望：1）应力计算使用的简化薄膜应力关系式十分简单，应当对此开发更加机理的应力模型；

2）高温中材料应变主要为蠕变，所以LHTCM模型计算应变仅考虑了蠕变应变的影响。虽然弹性等应变相比较蠕变较小，但也应当对应变模块进行补充以完善模型；

OLHF实验表明下封头在严重事故中变形十分显著，这种变形会对真实反应堆中的下封头换热和失效起到很大的影响［15］，然而LHTCM 模型缺乏计算变形的模块，这也是今后应当补充发展的方向。

作者贡献声明杨皓：软件开发、初稿准备；张斌：调研、方法论；高鹏程：修改文章，数据整理；唐绍伟：实验调研；单建强：修改文章。