石英脉型急倾斜极薄黑钨矿机械化 开采采场跨度优化研究

杨植根，郭恭祥，叶光祥

(1.江西盘古山钨业有限公司， 江西 于都县 342311； 2.赣州有色冶金研究所有限公司， 江西 赣州市 341000)

0 引言

某矿石英脉型急倾斜极薄黑钨矿属气化高温热液裂隙充填矿床，采用上向进路充填法开采矿脉带。受成矿裂隙成组成带分布影响，顶板矿、岩交替呈现，岩体稳定性较差，而采场跨度成为制约开采稳定性关键问题。

业界普遍以理论计算和数值模拟[1-2]的方式进行采场跨度的计算和优化，常用的理论计算方法有Mathews稳定性图表法[1]、简支梁[2]、悬臂梁[3]、工程跨度经验公式[4]等，常用的数值模拟软件有FLAC3D[5-7]、ANSYS[8]等。李小松等[9]基于假顶薄板理论得到了大跨度充填体假顶应力表达式；刘畅等[10]基于极限分析原理认为：长跨比＞2时，顶板安全厚度取决于跨度的大小；高谦等[11]、薛一鸣[12]则分别分析了大跨度采场失稳形式及失稳因素阈值。

本文通过RMR值和工程岩体分级标准进行了采场跨度初步设计，并在此基础上，选取了5组不同采场跨度，进行数值模拟稳定性分析，重点分析了采场应力、变形及破坏特征，最终得到最优采场跨度。

1 岩体分级

该石英脉型黑钨矿围岩为变质石英砂岩。岩体Q值为20.5，岩体力学参数见表1。

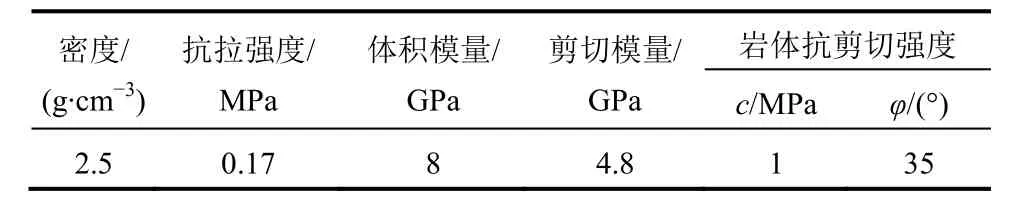
表1 变质石英砂岩力学参数

RMR与Q系统分级方法是目前普遍使用的岩体分级方法，许多学者总结出了两者之间相关性的经验公式，见表2。

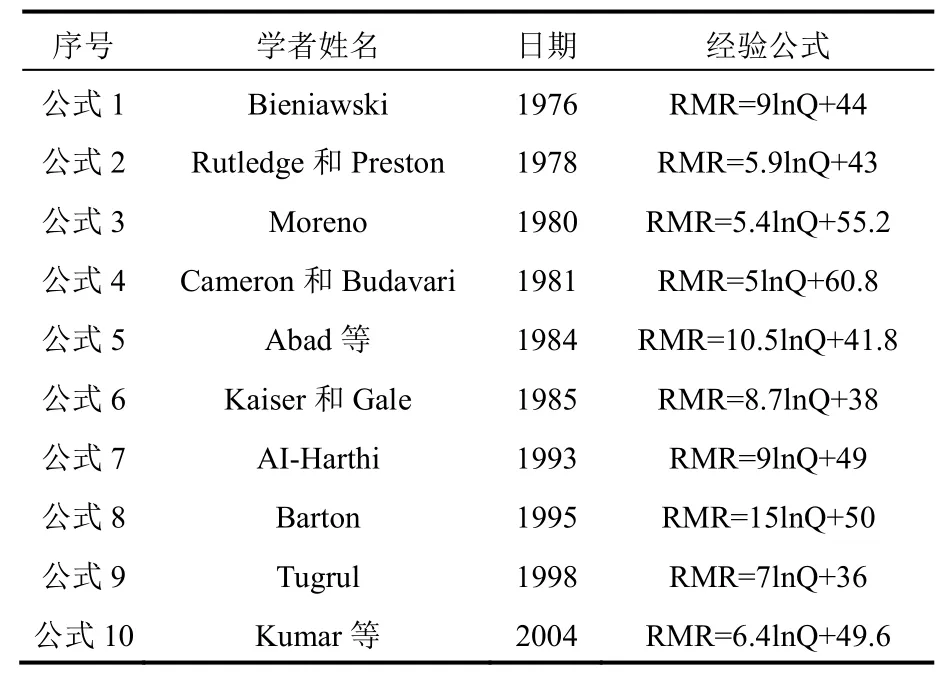
表2 RMR与Q分类相关关系式

根据以上经验公式，将Q值代入计算，得到RMR平均值为71，如图1所示。按照RMR岩体质量分级标准（见表3），该岩体为II级岩体。

2 岩体分级法

2.1 根据RMR值判断采场最大跨度

图2所示为根据RMR分级结果统计得到的无支护跨度与稳定时间图表。根据RMR稳定性经验 图表，当RMR值为71时，最大无支护跨度约为17 m，此时稳定时间不足2个月；当无支护跨度为 12 m左右时，稳定时间约为2个月；随着无支护跨度的减小，稳定时间增加。

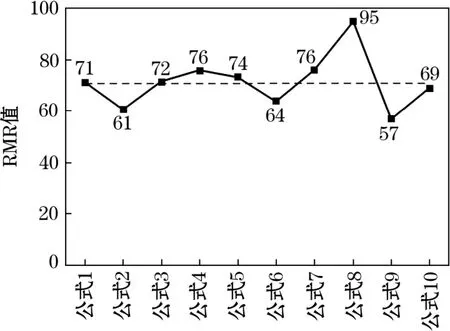
图1 RMR与Q转换计算结果

表3 RMR岩体质量分级标准

2.2 根据《工程岩体分级标准》判断采场最大跨度

根据《工程岩体分级标准》中关于地下工程岩体自稳能力的描述，当岩体质量等级为II级时，跨度小于10 m时，可长期稳定，偶有掉块，跨度为10～20 m时，可基本稳定，局部可发生掉块或小塌方。各岩体等级自稳能力见表4。

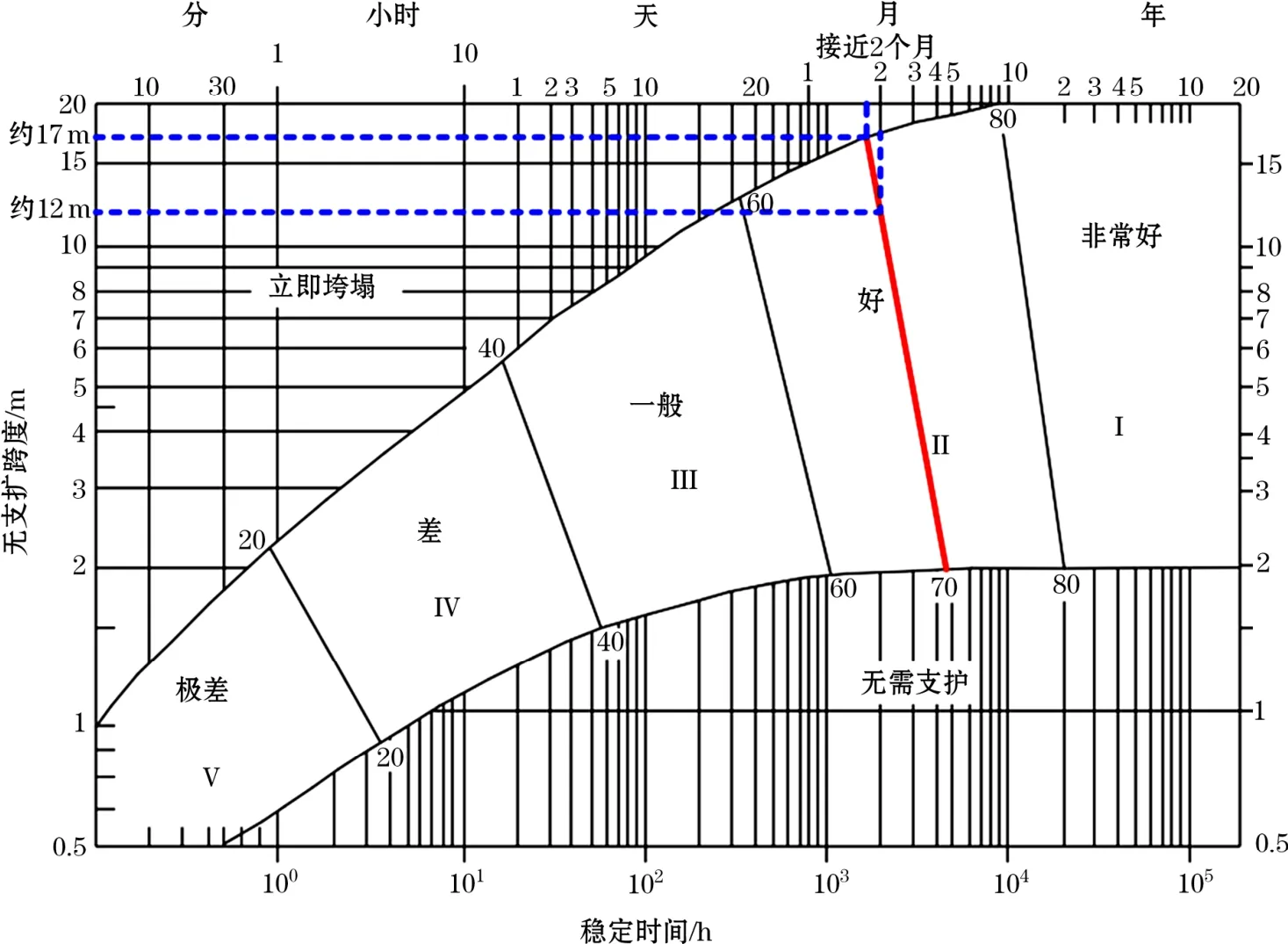
图2 基于RMR岩体分级的无支护跨度稳定性图表

表4 地下工程岩体自稳能力

2.3 小结

依据RMR无支护跨度稳定时间经验图表得到采场无支护跨度为17 m时，稳定时间不足2个月，无支护跨度为12 m时，稳定时间约2个月左右；依据《工程岩体分级标准》中关于地下工程岩体自稳能力的描述，II级岩体跨度小于10 m时，可长期稳定，跨度10～20 m时，可基本稳定。

综上所述，两种方法判断的采场自稳跨度范围基本一致，两者综合考虑，选取采场最大自稳跨度约为10 m。

3 数值模拟法

采用FLAC3D软件计算不同跨度采场稳定性，通过建立不同采场跨度模型，设置相同的边界条件与初始条件，根据岩体分级结果对岩体参数进行赋值，最终通过计算对比的方式验证并确定采场自稳跨度。

3.1 模型建立

根据岩体分级法确定的采场自稳跨度范围，建立5种采场跨度尺寸，分别为5 m、7.5 m、10 m、12.5 m和15 m。矿体为急倾斜矿体，因此采场高度对开采影响较小，此处采用控制变量法，统一采场高度为5m。由此建立了5种三维数值模拟模型，各模型网格与节点数量约30万个左右，模型如图3所示。

3.2 初始条件

矿山设计开采最深深度-120 m，建立该深度条件下自重应力产生的初始应力条件。矿体模型边界条件为：模型X法向平面施加X向约束，Y法向平面施加Y向约束，模型底面为固定约束，顶面为应 力边界条件，施加上覆岩层重力。

图3 5种不同跨度三维数值模型

3.3 计算结果分析

3.3.1 应力变化特征对比分析

图4为采场围岩最大主应力云图。不同跨度采场围岩的最大主应力分布规律相似，采场四周围岩为应力释放区域，采场侧帮围岩一定深度为应力集中区域。采场开挖后，上部覆岩荷载转移至采场两侧，于是在采场两侧围岩深部形成应力集中区域。

采集采场围岩内最大主应力数据，绘制采场围岩最大主应力随深度的变化曲线，结果如图5、图6所示。图5为采场顶板围岩内最大主应力随深度的变化曲线，不同跨度采场间曲线均呈现先增大后减小，而后逐渐趋于稳定的趋势，且不同跨度采场顶板浅部最大主应力大致相同，为3～4 MPa。但不同跨度采场最大主应力大小及其位置有着明显差异。采场为5 m跨度时，顶板围岩最大主应力极值为13 MPa，分布深度为2.8 m；7.5 m跨度时，最大主应力极值为12.3 MPa，深度3.6 m；10 m跨度时，最大主应力极值为11.4 MPa，深度4.7 m；12.5 m跨度时，最大主应力极值为11 MPa，深度6.5 m； 15 m跨度时，最大主应力极值为10.5 MPa，深度7.5 m。随着跨度的增加，采场顶板围岩应力扰动深度逐渐增加，表明更深部的围岩体发生变形。图6所示为采场侧帮围岩最大主应力随深度变化曲线。不同跨度采场侧帮应力集中深度差别不大，主要分布在3～4 m深的位置，最大主应力极值与采场跨度呈正相关。

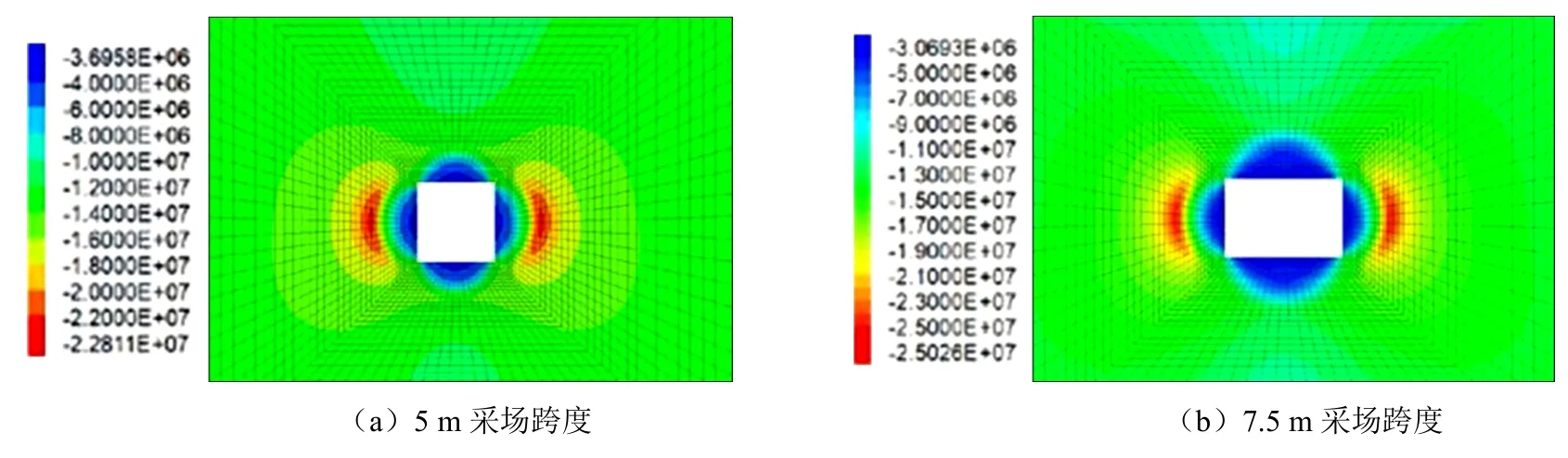
图4 不同跨度下采场围岩最大主应力云图

图5 采场顶板围岩最大主应力变化曲线

采场顶板与侧帮的应力曲线说明，该岩体条件 下，采场开挖造成的围岩体扰动主要发生在采场顶板，随着采场跨度的增大，顶板扰动越大，侧帮扰动无明显变化。

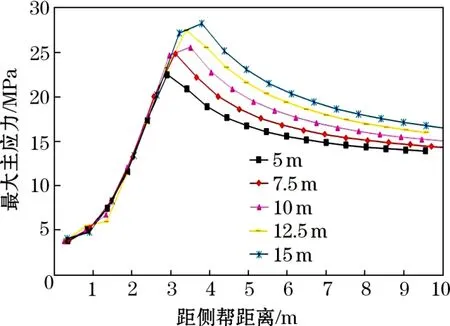
图6 采场侧帮围岩最大主应力变化曲线

图7为采场围岩最小主应力分布云图，采场四周围岩应力减小，向深部逐渐增加。采集采场顶板拉应力最大值，绘制拉应力值随采场跨度的变化曲线，如图8所示。岩石材料是一种抗压不抗拉的材料，因此采场顶板实际拉应力值越低越好。随着跨度的增加，采场顶板拉应力增大，在10 m跨度时 出现了急增的情况，各模型拉应力由0.04 MPa增加至0.16 MPa，小于岩体抗拉强度0.17 MPa。

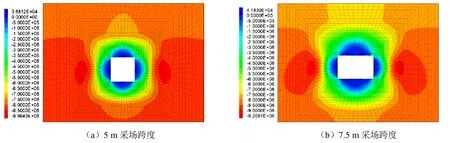
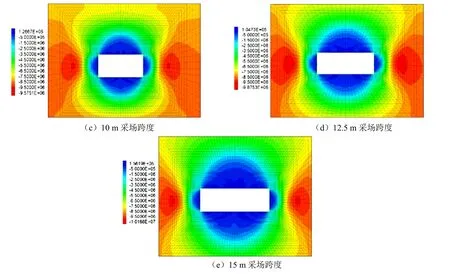
图7 不同跨度下采场围岩最小主应力云图

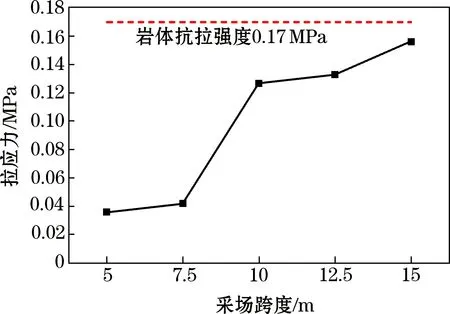
图8 采场顶板最大拉应力变化曲线

3.3.2 变形特征对比分析

图9为不同跨度下采场围岩位移云图，采场开挖后，顶板围岩受上覆荷载影响，主要发生竖向位移，且多见于采场顶板，两侧位移相对较小。顶板 围岩位移影响范围随着跨度的增加向上扩展，位移值也逐渐增大。根据图10可知，采场顶板最大位移值分别为0.96 cm、1.3 cm、1.7 cm、2.2 cm和2.6 cm。不同跨度采场顶板围岩最大位移值随采场跨度平稳增加，未发生较大突变。

3.3.3 矿岩破坏特征对比分析

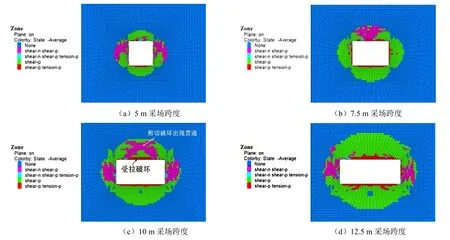
采场围岩塑性区表示了采场围岩内潜在破坏冒落区域和采场围岩松动圈范围。图11所示为不同跨度下采场围岩塑性区分布，根据采场塑性区分布图，塑性区有剪切与受拉塑性区。采场顶板拉塑性区在5 m、7.5 m跨度采场顶板出现较少，10 m跨度之后大量出现。采场围岩剪切塑性区随着跨度的变化，出现位置也逐渐演化。5 m跨度时主要在采场侧帮；7.5 m跨度时顶板开始出现；10 m跨度时采场顶板剪切破坏区出现贯通，形成潜在冒落楔形 体；采场为12.5 m、15 m跨度时，采场顶板围岩塑性区范围不断增大。根据图12，采场围岩塑性区厚度变化主要发生在顶板，随着采场跨度增加而扩大，由2.2 m逐渐增加至6.9 m，采场侧帮的塑性区则变化较小，均在3 m左右。该塑性区厚度变化对采场锚杆支护参数的选择具有指导意义。

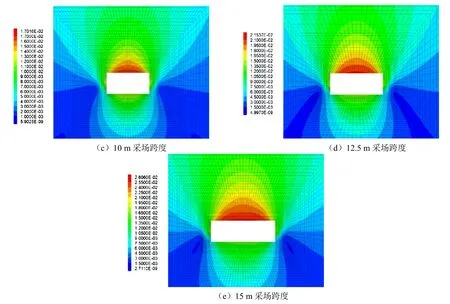
图9 不同跨度下采场围岩位移云图

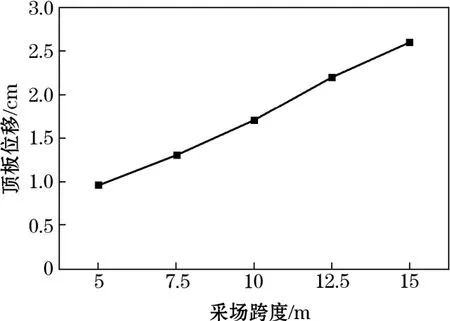
图10 采场顶板围岩位移变化曲线

3.5 小结

综上分析，采场开挖的扰动影响主要出现在采场顶板，且随跨度增加，影响范围、影响程度均有 扩大。具体表现为：随着采场跨度的增大，采场顶板拉应力极值增大，竖向位移、塑性区稳步增加，当采场跨度10 m时，顶板拉应力急增，剪切塑性区开始贯通，形成潜在冒落楔形体，且采场围岩开始出现较多拉塑性区。综合采场围岩应力、位移与塑性区变化特性，确定采场最优跨度为7.5 m。

图11 不同跨度下采场围岩塑性区分布

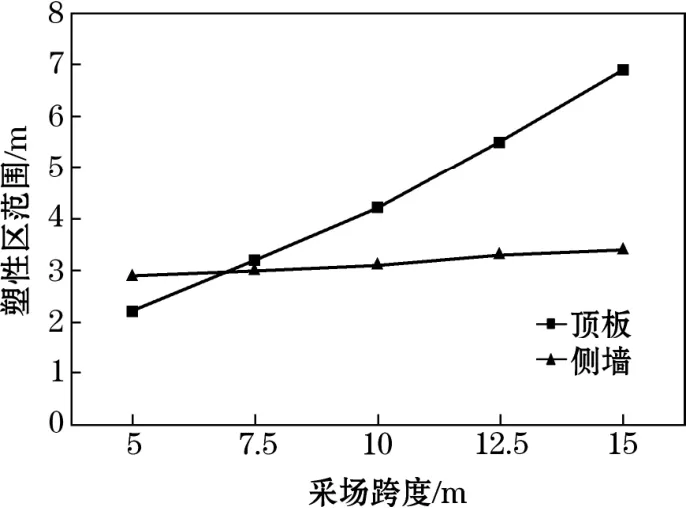
图12 采场围岩塑性区范围变化曲线

4 结论

本文采用岩体分级法与数值模拟法分别确定了采场最大自稳跨度。根据岩体分级法得到了采场最大自稳跨度为10 m，数值模拟法得到了最优采场跨度为7.5 m。综合两种方法研究结论，采场跨度取较小值7.5 m。

采场顶板稳定性的影响因素众多，由于地质条件的不确定性，采场稳定性主要受断层破碎带、地下水侵蚀以及爆破损伤的影响。当采场揭露的岩体质量条件发生变化时，应及时优化采场结构参数，并加强采场顶板支护。