振荡流下悬链线式立管涡激振动特性研究

陈殿鹏，顾洪禄，李福恒，李效民，郭海燕

（中国海洋大学 工程学院，山东 青岛 266100）

0 引 言

悬链线式立管（catenary type risers,CTRs）作为一种灵活性高、无需顶张力补偿的立管形式在深海油气开采中得到广泛应用。立管在一定的流场下，管道尾部两侧会交替出现一对漩涡，漩涡脱落会形成涡激升力致使立管产生周期性振动，该现象称为涡激振动（vortex-induced vibration,VIV）。当涡脱频率与结构固有频率在一定范围内相近时，结构会进入锁定（lock-in）状态，此时结构响应大幅、迅速地增大，立管更易产生疲劳失效。立管一旦被破坏会造成巨大的经济损失以及严重的海洋污染和次生灾害。因此，对CTR的VIV响应进行研究具有重要意义。

目前，国内外学者对垂直立管的VIV已经进行了广泛的数值研究，这些研究包括了理想状态下的均匀流[1-4]、剪切流[5-6]以及接近真实海况的振荡流[7-8]下垂直立管VIV 响应。但是，目前对于CTR（弯曲管）VIV 的数值模拟还较少。Srinil等[9]通过低阶流固耦合模型，研究了均匀流条件下CTR 涡激振动中的多模态相互作用；饶志标等[10]基于Shear7 软件分析了剪切流下CTR 振动位移和静态位移的关系；Meng等[11]基于能量守恒原理，通过Van der Pol方程定性地预测了内流速度对CTR-VIV 的影响；Tsukada 等[12]基于独立性准则预测了均匀流下CTR 升力幅值响应；Zhu 等[13]通过ANSYS MFX 软件中的求解器研究了指数剪切流下CTR 的漩涡脱落与结构运动之间的关系。综上所述，上述研究都是CTR 在理想稳恒流下的相关研究，对于接近真实海况的振荡流下CTR的VIV相关数值模拟尚未见报道。

本文基于向量式有限元理论，充分考虑了结构的几何非线性特征以及大变形等非线性行为，应用改进的尾流振子模型和独立性准则，对振荡流下顶张式立管以及均匀流下CTR 相关模型试验进行预测，进一步对振荡流下CTR 的VIV 特性从质点振动时程曲线、相图、流固能量传递以及响应峰值方面进行了分析，有望为CTR工程设计提供一定的参考。

1 基于向量式有限元的模型建立和求解

初始状态假设CTR 是一根有质量但无重力的斜梁，将其离散成N+1个集中质点，质点之间通过N个无质量梁单元连接。如图1 所示，以立管底部质点m1为原点建立坐标系，X轴水平向右，Z轴垂直X轴向上，Y轴垂直X-Z平面向内。根据已知初始边界条件，通过斜坡加载函数缓慢施加静力荷载（重力、浮力）并移动顶端质点mN+1至指定位置，最终得到CTR 的静力平衡位形。初始海流U 沿+X方向，立管初始曲率平面位于X-Z平面内。

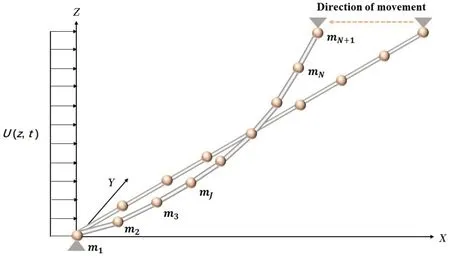
图1 向量式有限元中CTR立管模型Fig.1 CTR model in VFIFE

1.1 质点控制方程

在向量式有限元中，每个质点在三维空间下有三个平移自由度以及三个转动自由度。质点在一个时段内，位置发生改变，这个时段叫做途径单元。任意质点J在途径单元内的控制方程如下：

1.2 独立性原则

King[14]和Ramberg[15]试验研究发现，海流作用下倾斜立管的涡激升力以及旋涡脱落频率与海流垂直分量作用在与其等效的直管时相同，这个假设被称为独立性原则（independence principle）。

该原则首先将海流矢量分解为平行和垂直于立管平面的分量，如图2 所示。其中垂直于立管平面的海流分量Unh=Uel·sin(θ)，平行于立管平面的海流分量为Uel·cos(θ)。平面内分量可进一步分解为垂直于立管单元的分量，大小为Unv=Uel·cos(θ)·sin(α)，以及沿立管单元轴向的分量Uel·cos(θ)·cos(α)，如图3 所示。对于立管VIV 来说，其升力取决于垂直于该立管单元的有效海流矢量，并且其方向垂直于有效海流分量与该单元轴向组成的平面。垂直于立管的有效海流速度矢量由两个分量组成：垂直于立管平面的Unh和立管平面内的Unv。垂直于立管单元的有效海流速度Un=((Uel·sin(θ))2+(Uel·cos(θ)·sin(α))2)0.5，涡激升力方向如图4所示。

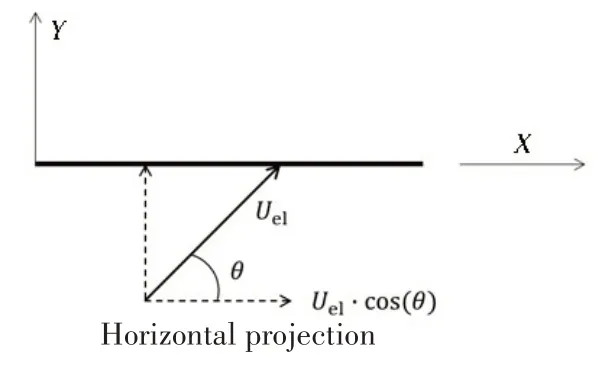
图2 平面外海流分解Fig.2 Decomposition of out-plane current

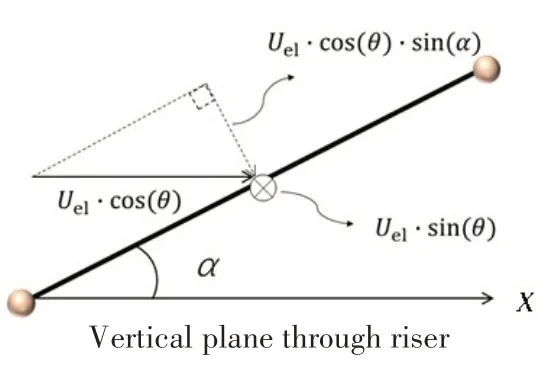
图3 平面内海流分解Fig.3 Decomposition of in-plane current

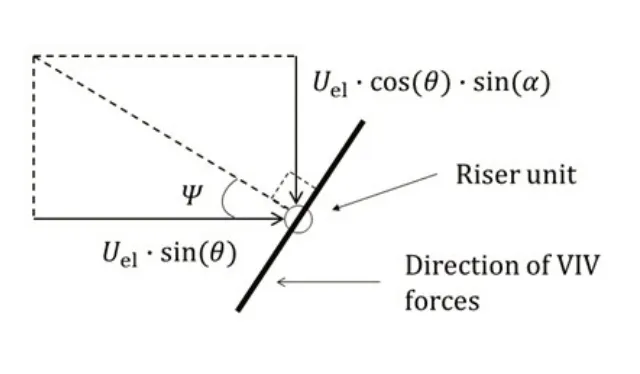
图4 升力方向Fig.4 Lift force direction

1.3 尾流振子方程

对于均匀流下CTR的VIV模拟，本文采用Fachinetti等[16]改进的尾流振子方程：

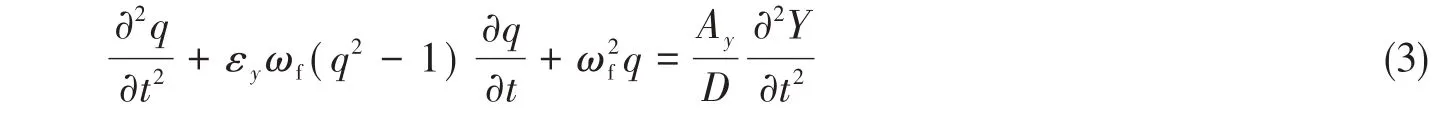
式中：q为尾流振子变量；εy为非线性项中的小参数，一般取0.3；Ay为流体动力参数，Ay= 12；ωf=2πStUn/D为漩涡脱落频率，St为Strouhal数，D为立管外径；Y为立管横向振动位移。

但上述尾流振子方程主要适用于稳恒流下立管VIV 的模拟，对于时变振荡流，许京[17]进一步对其进行了改进，引入无量纲时间tref=tωref和无量纲位移y=Y/D，其中ωref= 2πStUref/D为振荡流下漩涡脱落参考频率，Uref表示流速在一个变化周期内的平均值，也就是参考值。然后引入振荡海流参数得到如下方程：

1.4 控制方程求解

为了克服隐式时间积分带来的反复迭代求解以及收敛问题，本文通过中央差分法对n+1 时刻的质点位置向量、转角向量以及尾流振子变量q进行求解：

2 模型验证

2.1 振荡流下水平直管VIV验证

本文选取文献[19]的试验结果，将本文模型得到的模拟结果与其对比，结果如图5所示，左列为试验结果，右列为模拟结果。在该试验中，流速波动方程为

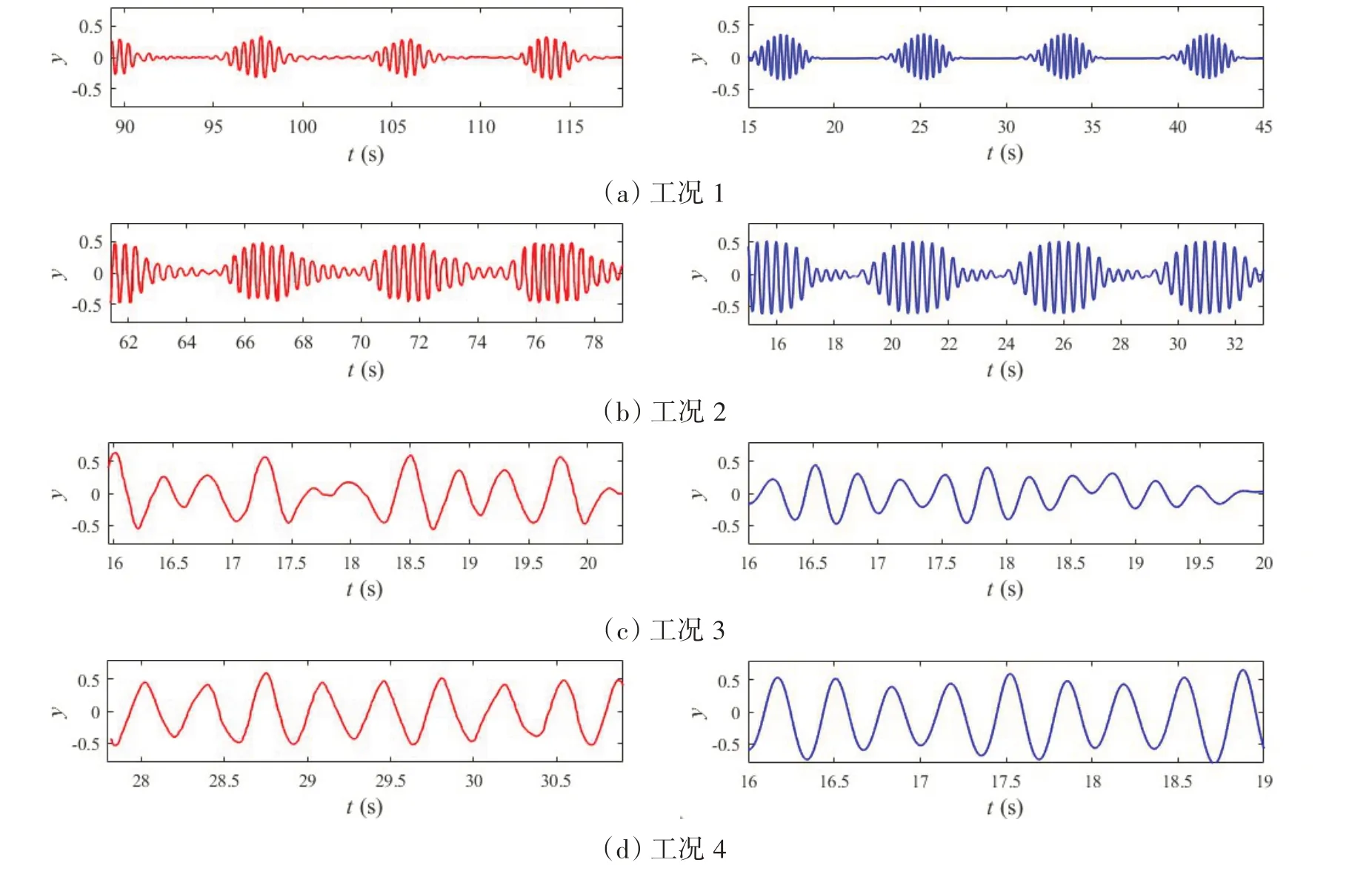
图5 工况1、2、3和4下z=2 m处VIV响应Fig.5 VIV response for Cases 1,2,3 and 4 at z=2 m

式中：Amax、Umax分别为海流最大振荡幅值和瞬时最大流速，T为振荡周期。对于振荡流来说，KC数是一个重要的描述参数，一般用KC数表示结构在水中运动的相对幅度。

立管具体参数见表1，根据文献[8]，本算例Strouhal数取0.2，同样选取两个典型工况组别：KC=178（大KC数工况）和KC=31（小KC数工况）进行验证分析，详细工况见表2。

表1 振荡流下柔性立管模型主要参数Tab.1 Main parameters of flexible riser model under oscillatory flow

表2 对比试验工况列表Tab.2 List of comparative test conditions

对于时变的振荡流下的结构响应来说，其响应模式极为复杂。但是，如图5所示，通过对比可以发现本文模型可以对上述特征现象进行较好的模拟，并且本文模型模拟的振动幅值和周期与试验结果吻合度较高。因此，一定程度上说明了本文模型在振荡流下预测结构VIV响应方面的有效性和准确性。

2.2 均匀流下CTR-VIV验证

为了进一步验证本文模型对于预测具备几何非线性结构形式（CTR）的VIV 响应有效性，选取文献[20]的试验结果与本文结果进行对比验证，其中立管模型参数见表3，本例质点总数取34。CTR 初始位形如图6 所示，其中海流流速U=0.26 m/s。由图7 可知，本文模型预测的模态数目和整体振动包络峰值与试验较为一致，并且与文献[20]的数值模拟结果相比，本文模型结果与试验结果更为吻合。经过上述验证，一定程度上证明了本文模型在计算CTR-VIV响应方面的有效性。

表3 CTR模型主要参数Tab.3 Main parameters of CTR model

图6 均匀流下CTR初始位形Fig.6 Initial configuration of CTR under uniform flow

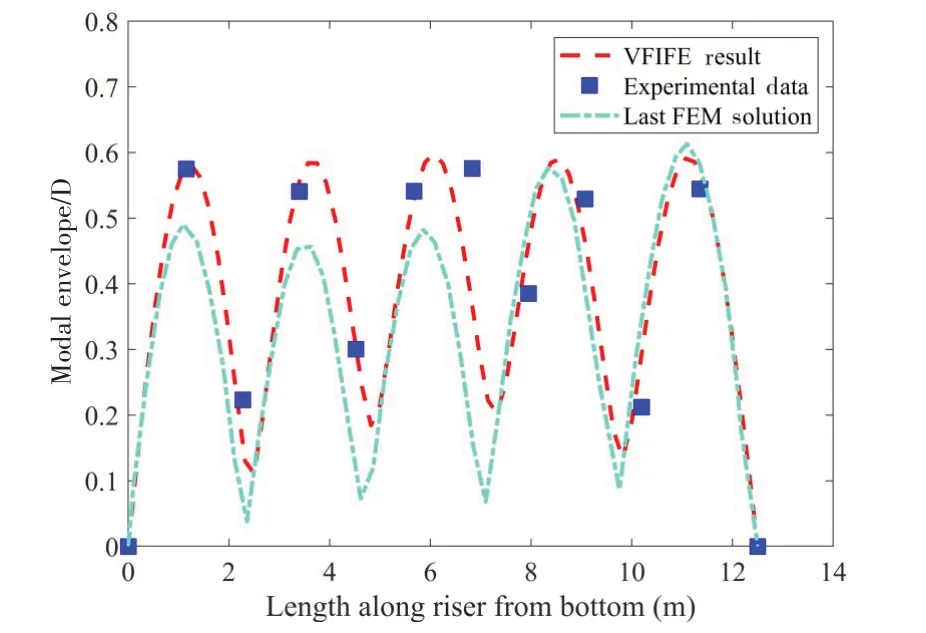
图7 文献[20]与本文得到的VIV包络图对比Fig.7 Comparison between results in Ref.[20]and the VIV envelope obtained in this paper

3 振荡流下CTR涡激振动分析

本章继续选取文献[20]中CTR 模型进行振荡流下的VIV 动力响应分析，分别取KC=20、40、60 和178 四种KC 数作为典型的振荡流工况，其中KC=178 代表的是较为典型的大KC数工况，KC=20、40 和60 代表小KC数工况。本章将从质点振动时程、相位图、流固能量传递以及结构响应峰值四个方面对振荡流下CTR-VIV进行分析。

3.1 质点振动时程响应分析

悬垂点是CTR 设计中关键的控制点，因此本文对CTR 悬垂点（Pt-30）在稳定时间30-40 s 的VIV响应进行分析，如图8所示，其中一、三、五行为流速U的时程变化，二、四、六行为悬垂点无量纲位移的时程变化。从图中可以看出，小KC数范围内，在相同Umax下，KC数越大，振荡海流激励下质点产生的响应幅值越小。这是因为随着KC数的增大，海流振荡周期随之增加，在一个较长的振荡周期内，海流更接近于均匀流的性质，这削弱了海流振荡幅值对立管的激励作用。同时，该现象也说明海流振荡周期和幅值同时控制着立管的VIV响应。

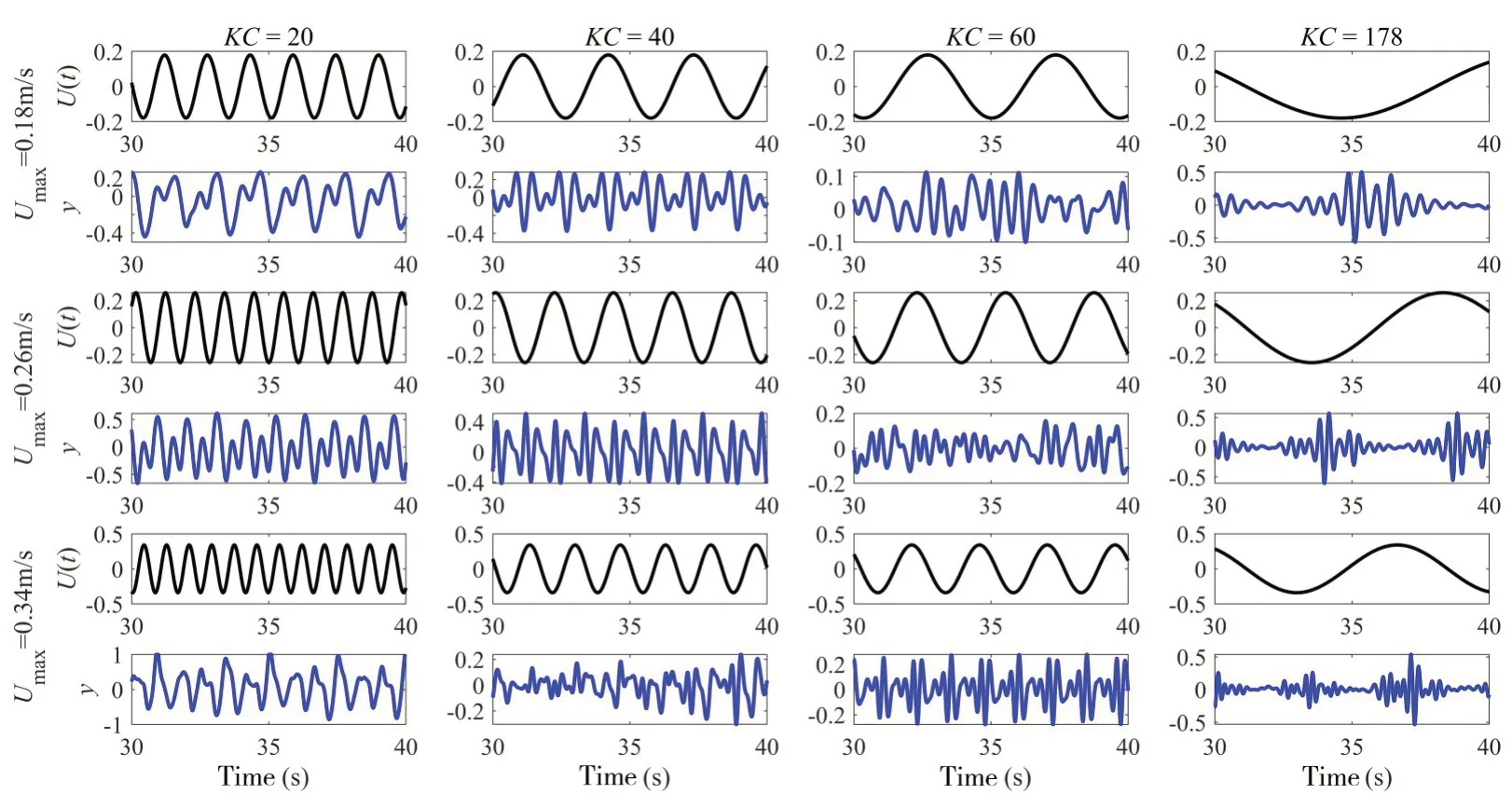
图8 不同KC数和不同最大流速下CTR悬垂点（Pt-30）的VIV响应Fig.8 VIV response at the CTR’s overhang point(Pt-30)at different KC numbers and Umax

另一方面，随着KC数增大，质点振动逐渐呈现典型的振幅调制现象。值得注意的是，这种振动幅值波动现象与均匀流下立管因模态转换而发生的拍频现象有着本质的区别。在KC=178（大KC数）工况下，这种振幅调制现象更为剧烈，质点振动产生如文献[19]所述的建立、锁定、衰减三个特征阶段。海流速度接近为0的时候，质点几乎不振动，出现“间歇性VIV”现象，这可能是由于立管响应与时变海流之间存在迟滞现象，文献[8]同样指出这种现象在大KC数下更为明显。在KC=20 下，Umax的增加对立管VIV 响应幅值影响较大，但随着KC数增大，Umax对于立管VIV 响应无明显影响，这与均匀流下流速作为关键参数控制结构响应有着显著的不同。本文也研究了其他位置点，结果都与悬垂点响应特征一致。并且，上述相关特征与振荡流下直管的VIV响应特征较为相近，这说明CTR的曲率特征对振荡流下结构响应特性无明显影响。

3.2 相图分析

图9是CTR悬垂点Pt-30在KC=20、40、60和178下，流速分别为Umax=0.18 m/s、0.26 m/s和0.34 m/s，时间间隔为30～40 s 下的质点振动相图。其中横坐标是无量纲横向振动位移y，纵坐标是无量纲振动速度∂y/∂t。从图中可以看出，不同KC数下质点的相图主形状有着显著差异，并且这种差异与Umax关联性较小。KC=20、40、60 和178 下质点相图形状分别呈“苹果形”、“心形”、“双圆环形”和“玫瑰形”。其中，由于海流的时变性导致立管响应呈现一定的随机性，进而导致相图呈混沌状态，KC数越大，混沌状态越明显。

图9 不同KC数和不同最大流速下CTR悬垂点（Pt-30）的振动相图Fig.9 Phase portrait of the Pt-30 at different KC numbers and Umax

3.3 流固能量传递特性分析

流体与固体之间的能量传递不仅可以从VIV 机理角度较好地解释立管振动特性，而且可以为实际立管设计提供理论指导。瞬时流固能量传递公式为[21]

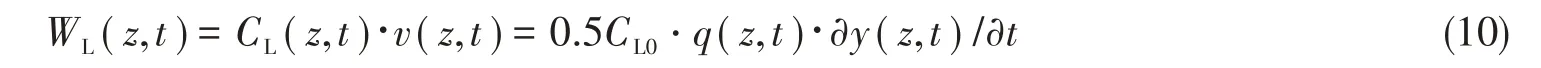
式中，WL为瞬时能量传递量，v是质点横向振动速度，CL为升力系数。图10 给出了KC=20、40、60 和178，Umax=0.26 m/s 下CTR 的能量传递时空分布，在小KC数范围内（KC=20、40 和60），能量传递峰值分别为0.16、0.11 和0.05，随着KC数增大能量传递峰值呈递减趋势。在KC=178 下能量传递峰值并没有进一步增大，这是因为结构在振荡流下产生的间歇性VIV 会导致能量在流体阻尼以及自身阻尼的影响下产生折损。并且在KC=60 时，能量传递随时间变化无周期性可言，处于不稳定的传递状态，这可能是由于此时海流激励能量与结构阻尼处于不平衡转换状态导致。当KC数进一步增大时，能量传递再次呈现一定的周期性。

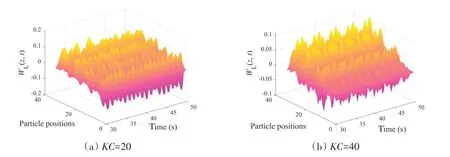
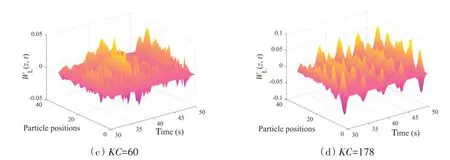
图10 不同KC数下流固能量传递时空分布Fig.10 Space-time distribution of energy transfer at different KC numbers

在四种KC数下，能量传递峰值都出现在立管悬垂段。能量传递沿立管全长呈现非对称性，逐渐向支座两边递减。这是由于模型中考虑了CTR几何非线性特征，根据独立性原则，立管悬垂段处的海流有效分量最大，因此悬垂段受海流激励产生的能量更多。并且值得注意的是，不同KC数下，立管都产生了负能量传递现象，即能量从立管向海流传递，这与我们的直观判断相悖。根据公式（10）可知，这是由于升力系数与速度产生相位差导致其乘积为负值，这种现象在文献[22]中剪切流下直管VIV模拟中也出现过，并且这种现象同样发生在等效低流速区域（立管下部），继而形成结构阻尼区。这主要是与有效流速剖面的不均匀分布有关，才导致了立管向流体传递能量，即负能量传递现象。

3.4 CTR最大振动幅值分析

图11 是KC=20、40、60 和178 下CTR 整体响应最大值ymax随最大流速Umax的变化趋势图。由图11可知，在小KC数范围内，在相同Umax下，KC数越大，立管VIV 响应峰值越小。这是因为在较高KC数下，水动力阻尼对于结构响应有明显抑制作用，随着KC数减小，水动力阻尼对结构影响逐渐减弱。而大KC数下，立管响应峰值再次回落，这可能与其涡脱落对数量以及特征模式有关。在振荡流下，由于立管在时变激励下会产生较为不稳定的模态切换，因此其振动响应峰值会随着流速变化出现“多峰”现象，这种现象在文献[23]中同样出现，在KC=20 时，“多峰”现象更为显著。

图11 不同KC数下VIV响应峰值随最大流速变化Fig.11 Peak of VIV response versus Umax at different KC numbers

4 结 论

本文基于向量式有限元理论对振荡流下CTR-VIV 响应进行了研究，将本文结果与相应的试验结果对比，在一定程度上验证了本模型的有效性。进一步对KC=20、40、60 和178 的振荡流下的CTRVIV响应特性进行了分析，由分析结果可得到如下结论：

（1）海流振荡周期和幅值同时制约着立管振动响应幅值；在小KC数下，立管在振荡流激励下产生振幅调制现象，在大KC数下质点振动响应进一步呈现明显的间歇性涡激振动现象。值得说明的是，CTR的曲率特征对振荡流下结构响应特性无明显影响。

（2）KC=20、40、60 和178 下质点振动相图主形状分别呈“苹果形”、“心形”、“双圆环形”和“玫瑰形”，其中Umax对质点振动相图形状影响不大；振荡流下质点振动具有一定的随机性，随着KC数的增大，相图混沌状态的趋势更为显著。

（3）在小KC数范围内（KC=20、40、60），随着KC数增大，流固能量传递峰值逐渐减小，这是由于KC数较大时，结构的不稳定振动状态导致能量传递损耗；由于CTR 的曲率特征导致的不均匀有效海流剖面，使立管在底部低等效流速区域产生局部阻尼区，因此产生负能量传递现象。

（4）在小KC数范围内，KC数越大，由于水动力阻尼的影响，在相同Umax下立管被激励产生的响应峰值ymax越小，随着KC数减小，水动力阻尼对其影响衰减；由于大KC数下结构具备特征的涡脱模式，因此导致其响应与小KC数下有着本质的不同。