考虑平台作用的顶张式立管动力分析
李艳丽, 黄维平, 常 爽 , 柳振海,3
(1.上海船舶运输科学研究所 a.航运技术交通行业重点实验室;b.航运技术与安全国家重点实验室,上海 200135;2.中国海洋大学 工程学院,山东 青岛 266100;3.浙江省电力设计院,杭州 310012)
0 引 言
深水顶张紧式立管在深水油气开发领域有着广泛应用,其结构在形式上表现为内层油管分别被内套管和外套管包裹,套管用于提供隔离保护作用,套管之间有扶正器作为支撑,以避免发生碰撞事故损伤立管。目前国内外学者已对多层立管进行大量研究。在双套管立管方面:罗坤洪等[1]以两端铰支的多层耦合立管为研究对象,建立了多层立管耦合模型,运用MATLAB软件对深水顶张式立管的全耦合动力响应和参数敏感性进行了分析。在单套管立管方面:康庄等[2]运用Orcaflex软件研究了立管顶部预张力对立管结构强度的影响;张崎等[3]运用Abaqus软件对单套管立管的非线性时域运动进行了研究;MAN等[4]和YUE等[5]提出了一个数学模型,研究了重力、压力和热膨胀等因素在立管纵向引起的应变;ZHOU等[6]对单套管管中管模型的非线性应力进行了研究;赵炳星[7]运用Abaqus立管分析软件提供的间隙模型模拟了管中管模型,分别结合顶张力系数、内外管间隙、海流和波浪等参数对立管进行了参数敏感性分析。
目前,在已有的深水顶张式立管设计研究中,多采用等效管(按照截面刚度等效)进行模拟分析,没有考虑立管间复杂的耦合作用;同时,对双套管立管的研究大多以两端铰支的多层耦合立管为研究对象,没有考虑上部平台和管间间隙对立管耦合运动的影响。在实际设计中,立管采用双套管结构,且顶端与平台链接,底端铰支,因此有必要对该立管进行建模分析。
本文首先根据假设条件建立数学模型,其次给出考虑立管管间间隙的各层立管动力响应运动方程的迭代求解过程,然后分析不同扶正器布置间距下,各层立管相同节点处的耦合动力响应,绘制各层立管相同节点处的相对位移与立管管间间隙的比值的时程图,最后分析各层立管的弯曲应力,绘制各层立管相同节点处的弯曲应力比值时程图。
1 数学模型
建立立管模型(见图1),其中:立管的顶端与平台连接,底端固定于海底;仅考虑波浪载荷的作用,波浪方向为x方向;坐标零点位于立管轴线底端中线处。
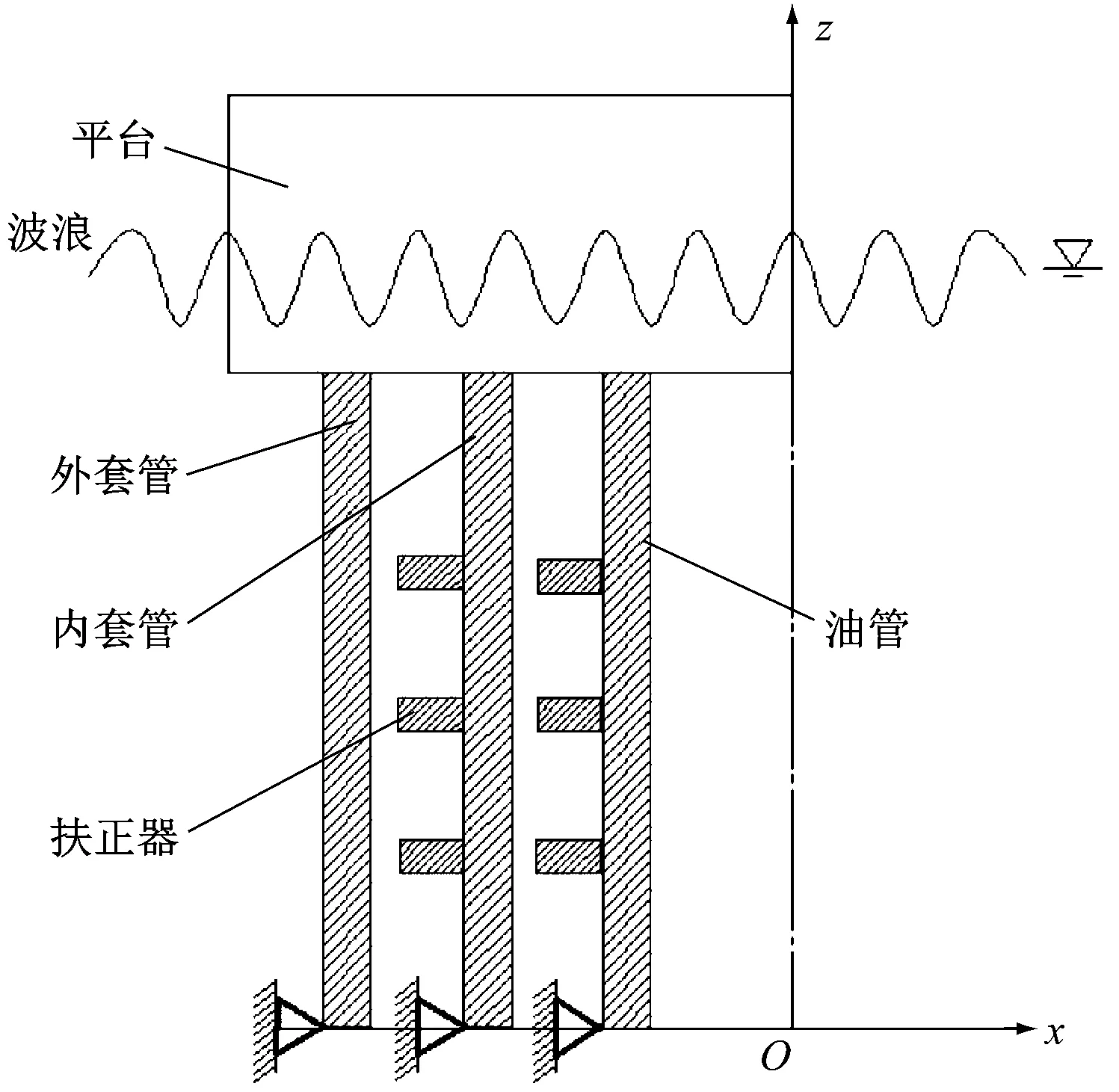
图1 立管系统左侧剖面模型
平台运动对各层立管的动力响应有很大影响,不可忽略。在Orcaflex软件的辅助下,按照弯曲刚度等效的原则模拟计算等效管和平台在环境载荷下的运动响应,有
EIeq=EIo+EIi+EIy
(1)
式(1)中:E为杨氏模量;Io、Ii和Iy分别为外套管、内套管和油管的惯性矩;Ieq为等效管惯性矩。
平台沿x轴的运动响应与各层立管顶端节点的响应一致,可将各层立管顶端节点的响应变换为作用于各层立管顶端的顶张力和横向作用力。
对于长细形顶张式立管,可忽略其剪切变形。因此,该类型立管的横向弯曲振动问题可采用Euler-Bernoulli梁的复杂弯曲理论求解,各层立管均为均质等截面管。沿x轴建立各层立管的有限元模型,采用newmark-β法的增量型式进行动力响应分析,可得到基本形式的3层立管的运动控制方程为
(2)
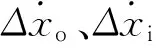
2 数值计算
2.1 立管接触条件
管柱间隙的存在会对耦合方程产生影响,根据图1所示模型,相邻立管之间的相对位移为
(3)
(σt+Δt)2=(xi)t+Δt-(xy)t+h2
(4)
式(3)和式(4)中:(σt+Δt)1为外套管与内套管在扶正器位置处的相对位移;(σt+Δt)2为内套管与油管在扶正器位置处的相对位移;(xo)t+Δt为外套管在t+Δt时刻的位移;(xi)t+Δt为内套管在t+Δt时刻的位移;h1为外套管与内套管之间扶正器的高度;h2为内套管与油管之间扶正器的高度;Di为内套管的外径;di为内套管的内径。
在t时刻,外套管和内套管在扶正器处的接触条件为
(5)
式(5)中:上、下2个不等式分别为外套管和内套管在轴线左侧接触和右侧接触时的判断条件。
在t时刻,内套管和油管在扶正器处的接触条件为
(6)
式(6)中:Dy为油管的外径;上、下2个不等式分别为内套管和油管在轴线左侧接触和右侧接触时的判断条件。
当外套管与内套管在扶正器s处的相对位移在t+Δt时刻满足式(5),或内套管与油管在扶正器s处的相对位移在t+Δt时刻满足式(6)时,接触节点s处的位移需通过迭代求得。
2.2 迭代运算
由Newmark-β法公式,有
(7)
(8)
(9)
式(7)~式(9)中:γ和β为与精度和稳定性有关的参数。将式(2)变换为式(7)的形式,可得
(10)
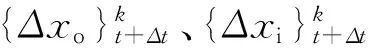
图2为立管系统左侧剖面接触示意。当外套管与内套管在t+Δt时刻的相对位移满足式(5)时,从图2a中可看出,外套管与内套管在t+Δt时刻的相对位移满足
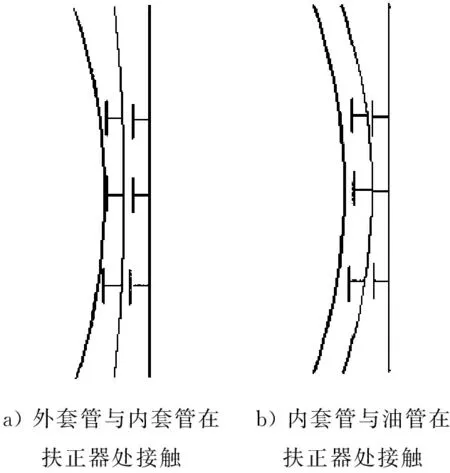
图2 立管系统左侧剖面接触示意
(11)
(12)
式(11)为在t时刻满足式(5)时外套管与内套管的位移关系;式(12)为在t时刻不满足式(5)时外套管与内套管的位移关系。
同理,当内套管与油管在t+Δt时刻的相对位移满足式(6)时,从图2b中可看出,外套管与内套管在t+Δt时刻的相对位移满足
(13)
(14)
式(13)为在t时刻满足式(6)时内套管与油管的位移关系;式(14)为在t时刻不满足式(6)时内套管与油管的位移关系。
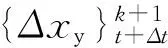
迭代终止条件为
(15)
式(15)中:ε为迭代终止条件最大值。当满足式(15)时,停止迭代。迭代结束之后,即可计算各层立管在接触点s处的速度和加速度增量,计算式为
(16)
(17)
计算立管其他节点i的位移增量、速度增量和加速度增量,有
(18)
(19)
(20)
(21)
3 算例分析
计算模型如图1所示。张力腿平台参数:立柱间距为86.25 m;工作水深为1 500 m;排水量为5.45×107kg;平台纵摇转动惯量为8.237×108kN·m2;平台艏摇转动惯量为9.807×108kN·m2;张力腿总预张力为1.373×105kN(顶张力按各层立管的轴向刚度比率分配)。管中管结构主要参数见表1。采用JONSWAP谱模拟随机海浪,特征波高Hs=8.3 m,峰值周期Tp=9.7 s。计算采用本文开发的Tube2D软件,将立管模型划分为1 500个单元,时间步长为0.1 s。
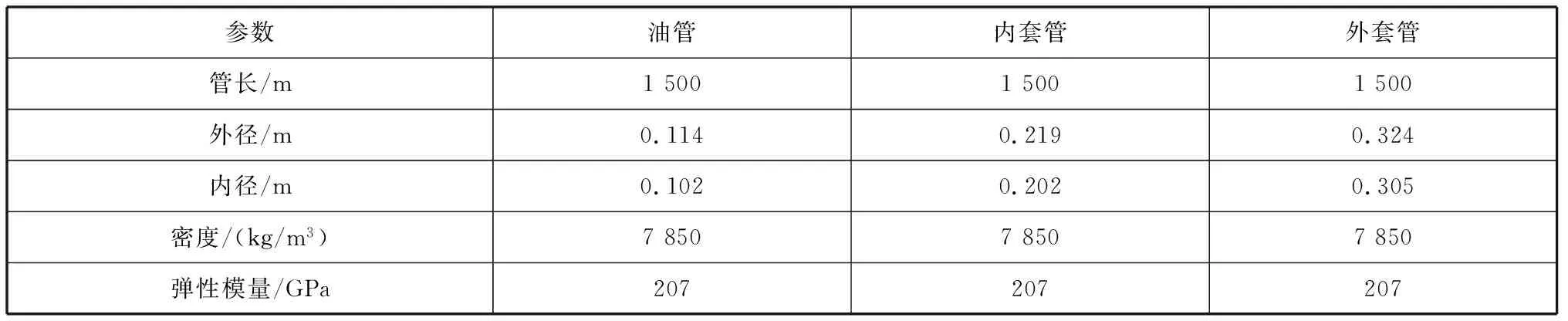
表1 管中管结构主要参数
3.1 平台运动响应时程图
由于本文的主要研究对象为二维平面的顶张式立管,因此仅给出波浪入射角为0°时,张力腿平台的纵荡响应时程图、纵摇响应时程图、纵荡速度时程图和纵摇角速度时程图,见图3~图6。
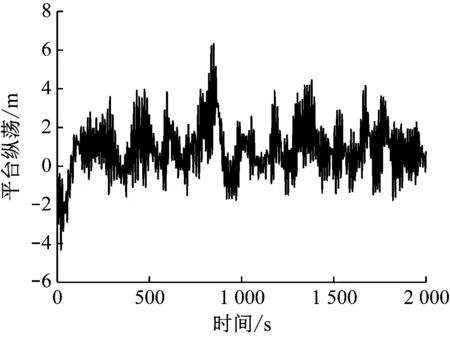
图3 平台纵荡响应时程图
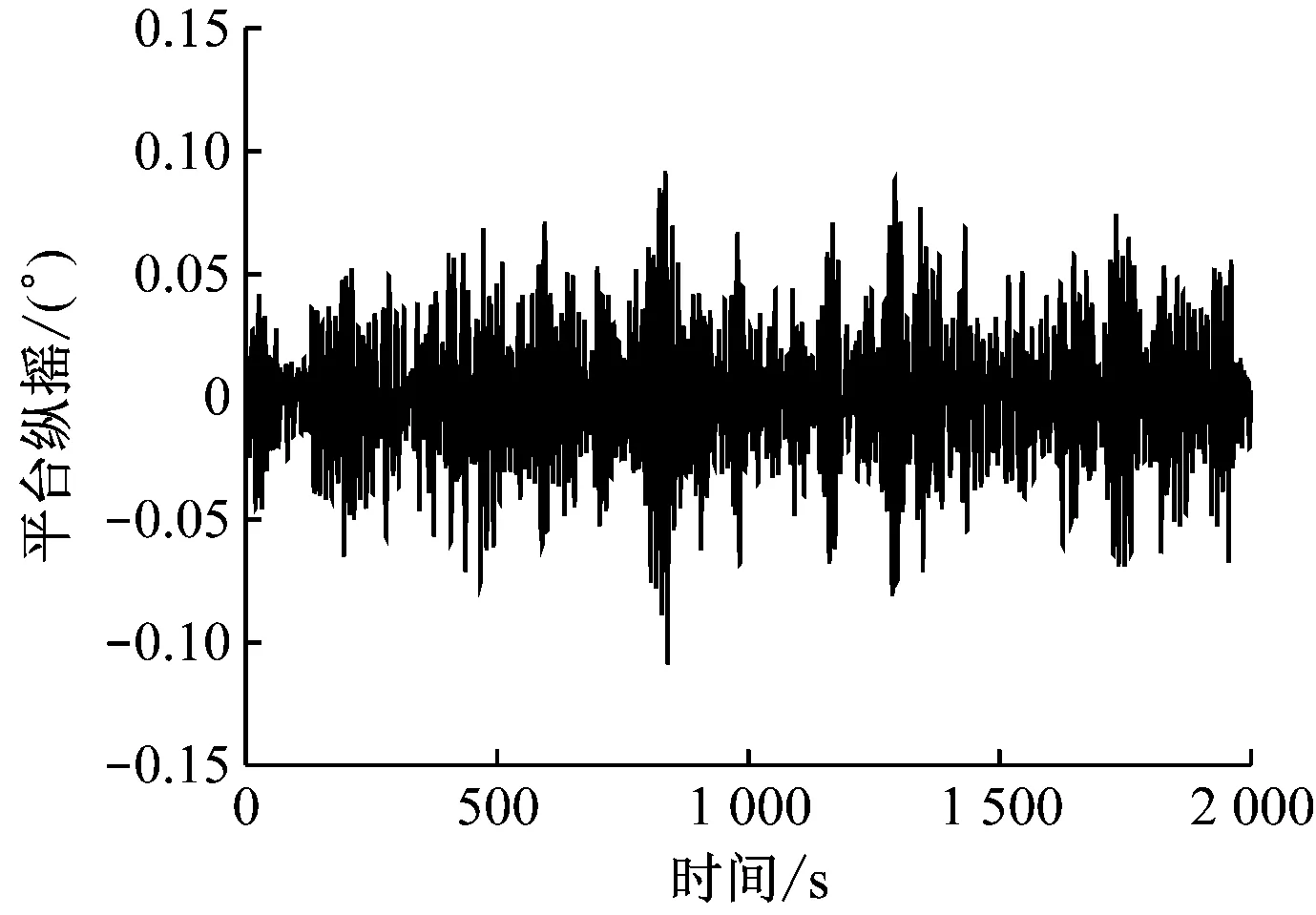
图4 平台纵摇响应时程图
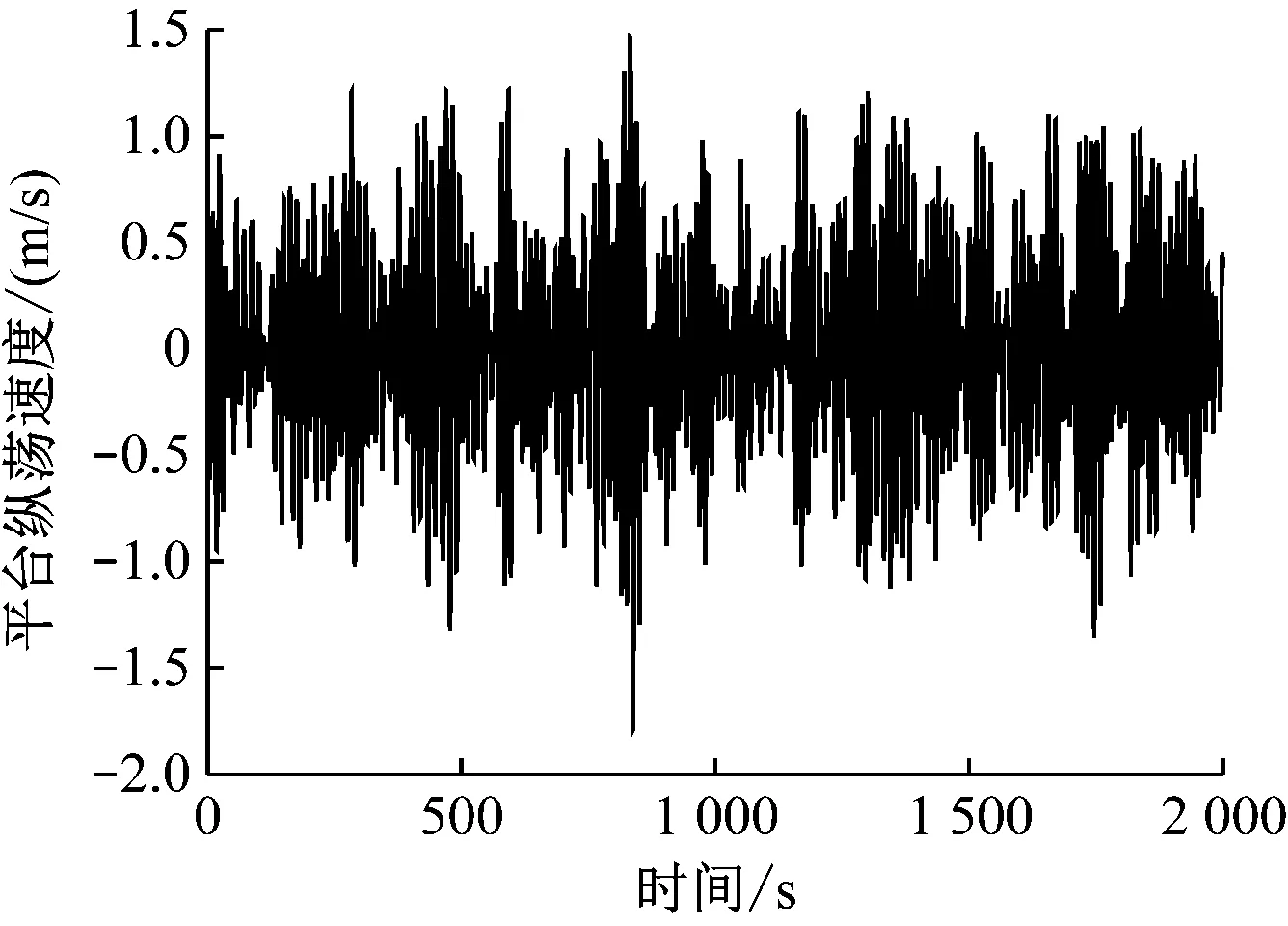
图5 平台纵荡速度时程图
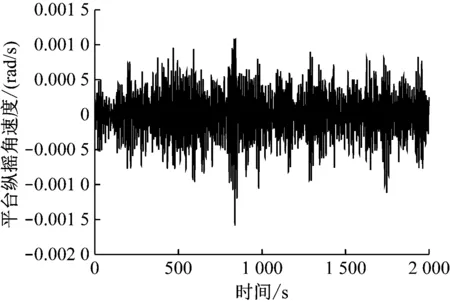
图6 平台纵摇角速度时程图
3.2 立管动力响应分析
图7~图10为管间扶正器的布置间距为25 m时,立管20 m和1 485 m处的响应时程图和相邻立管的无量纲化相对位移曲线(其中Δx和p分别为相邻2层立管的相对位移和间隙),顶张力系数为1.2。图11~图14为扶正器的布置间距为40 m时,立管20 m和1 485 m处的响应时程图和相邻立管的无量纲化相对位移曲线,顶张力系数为1.2。
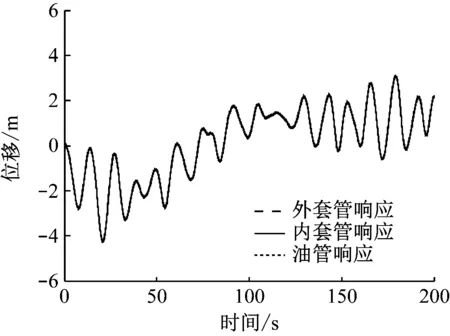
图7 耦合立管20 m处响应时程图
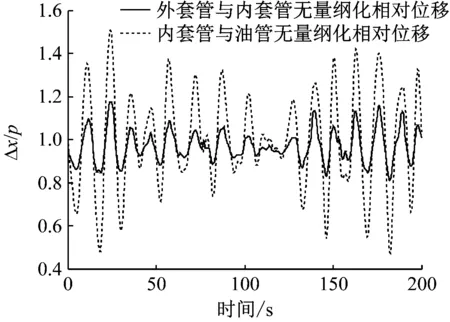
图8 耦合立管20 m处无量纲化相对位移曲线
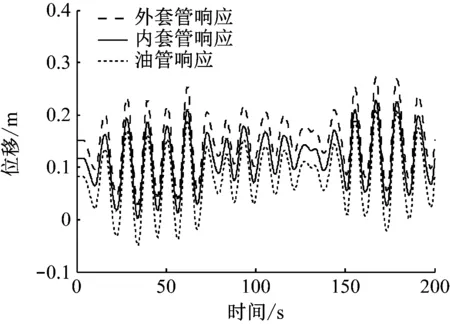
图9 耦合立管1 485 m处响应时程图
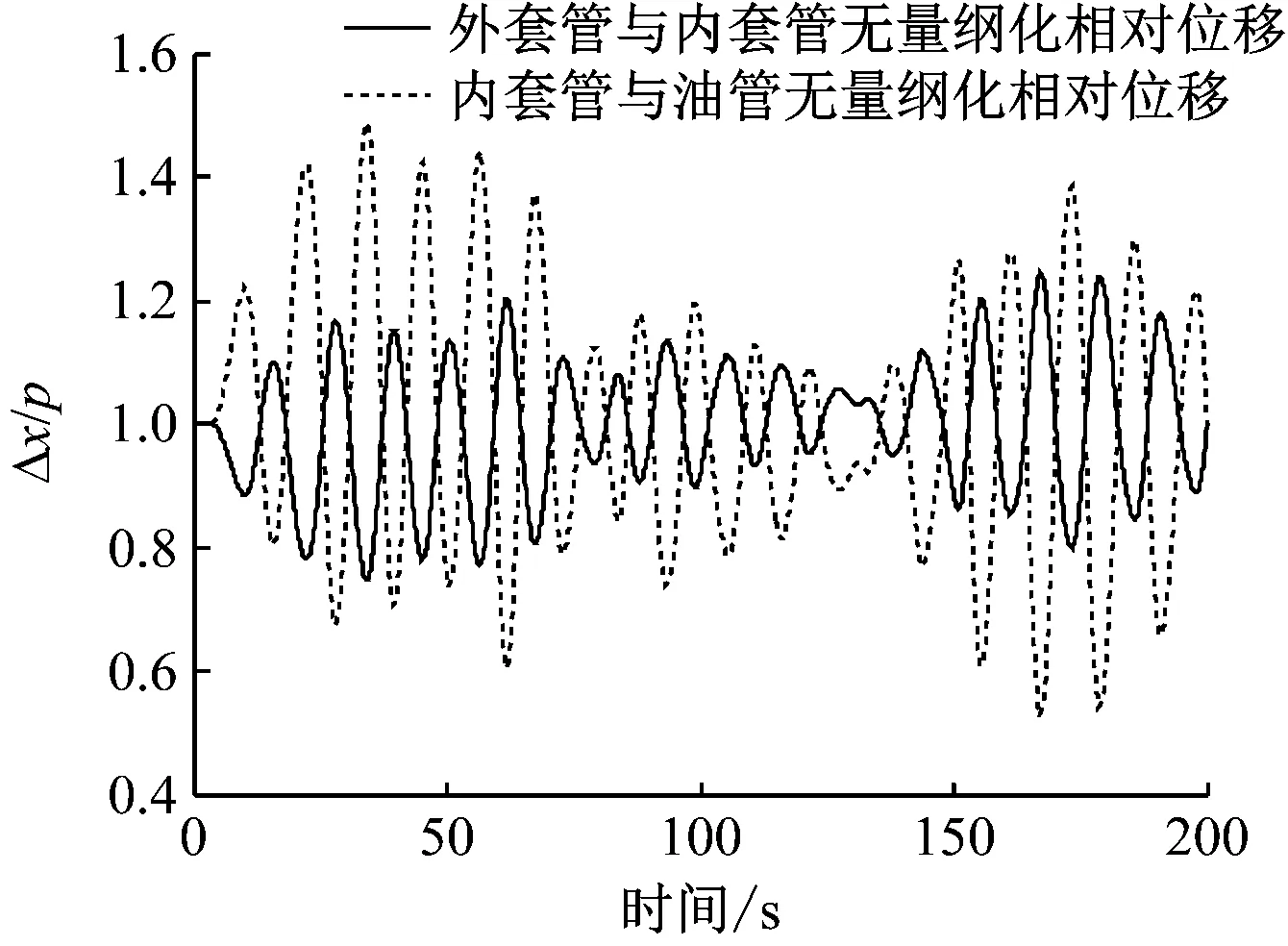
图10 耦合立管1 485 m处无量纲化相对位移曲线
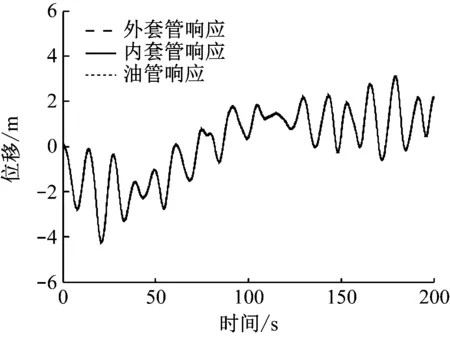
图11 耦合立管20 m处响应时程图
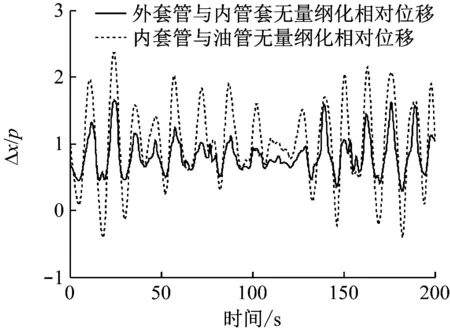
图12 耦合立管20 m处无量纲化相对位移曲线
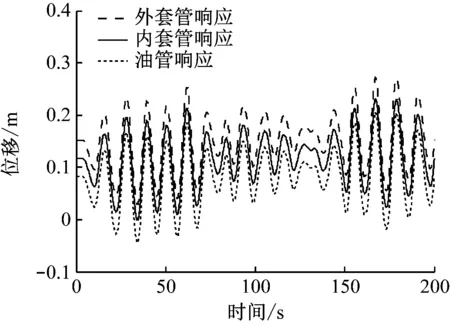
图13 耦合立管1 485 m处响应时程图
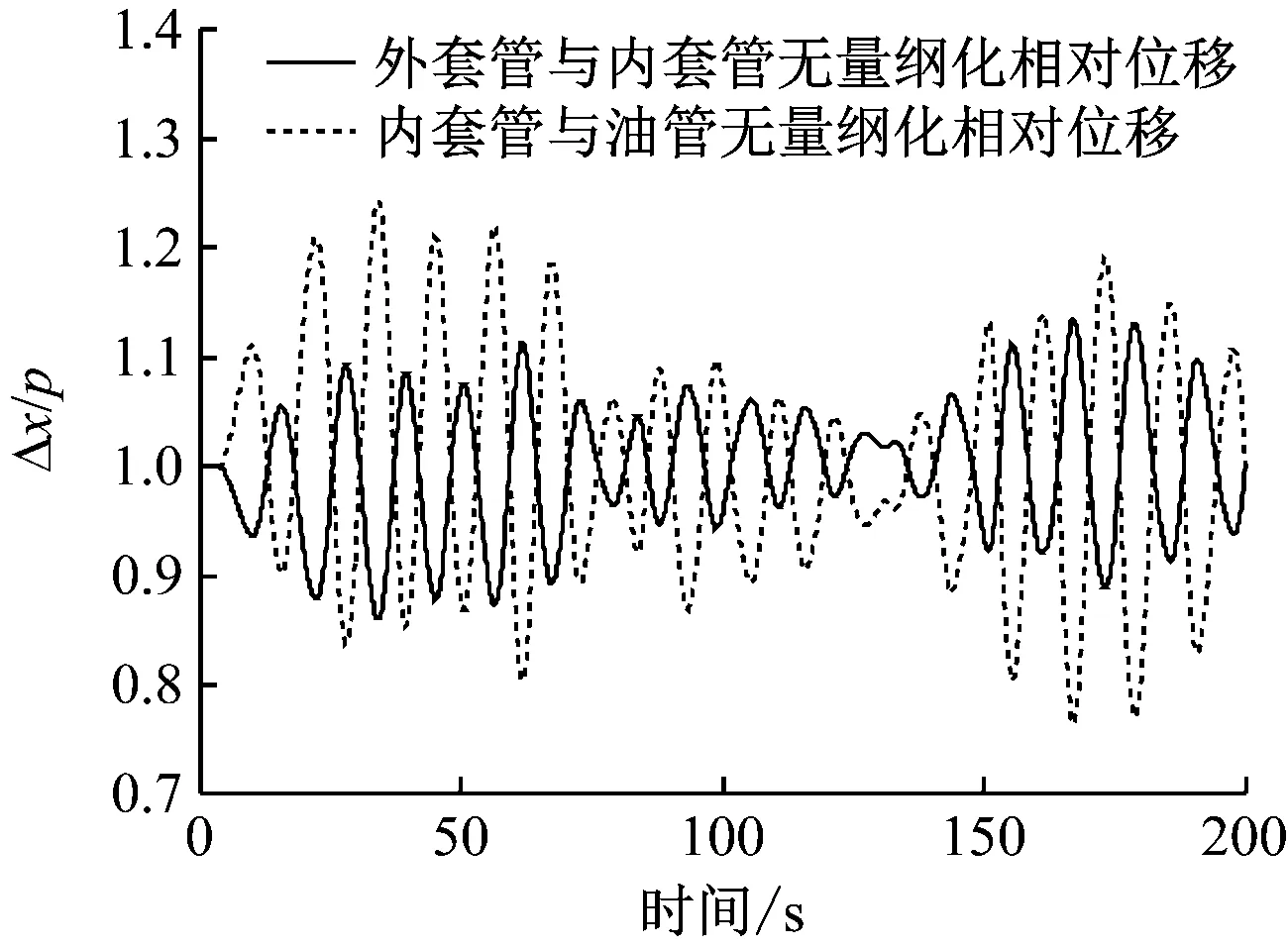
图14 耦合立管1 485 m处无量纲化相对位移曲线
由图7和图11可知,扶正器的布置间距对立管顶端20 m处响应幅值的影响不大。由图8和图12可知,当扶正器的布置间距为40 m时,内套管与油管20 m处的相对位移曲线幅值大于0且小于2,说明此时内套管与油管管体发生碰撞。这与文献[1]中的立管两端铰支分析有所不同,在文献[1]中,当扶正器间距为40 m时,外管与内管在20 m处发生碰撞。造成这种差别的原因是立管上部运动受平台运动的影响较大。
由图9和图13可知,扶正器的布置间距对立管1 485 m处响应幅值的影响较小。由图10和图14可知,当扶正器的布置间距增大时,立管间的相对位移有所减小,这是因为扶正器数量减少,其传递的载荷相对减小,平台运动对立管底端的影响减小。
3.3 弯曲应力分析
图15为扶正器布置间距为25 m、顶张力系数为1.2时,立管85 m处弯曲应力时程图。图16~图18分别为各层立管弯曲应力与总弯曲应力的比值时程图,分别绘制了外套管、内套管和油管的弯曲应力占三者总弯曲应力的比例随时间的变化情况,用以研究各层立管所受弯曲应力是否按立管弯曲刚度之比分配,并分析其原因。
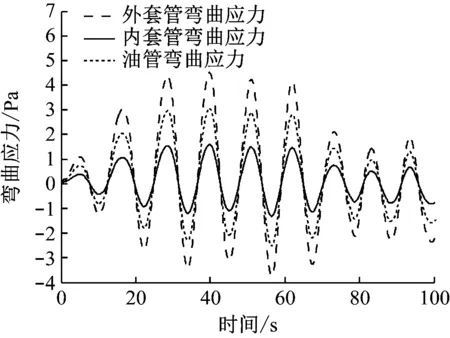
图15 立管85 m处弯曲应力时程图
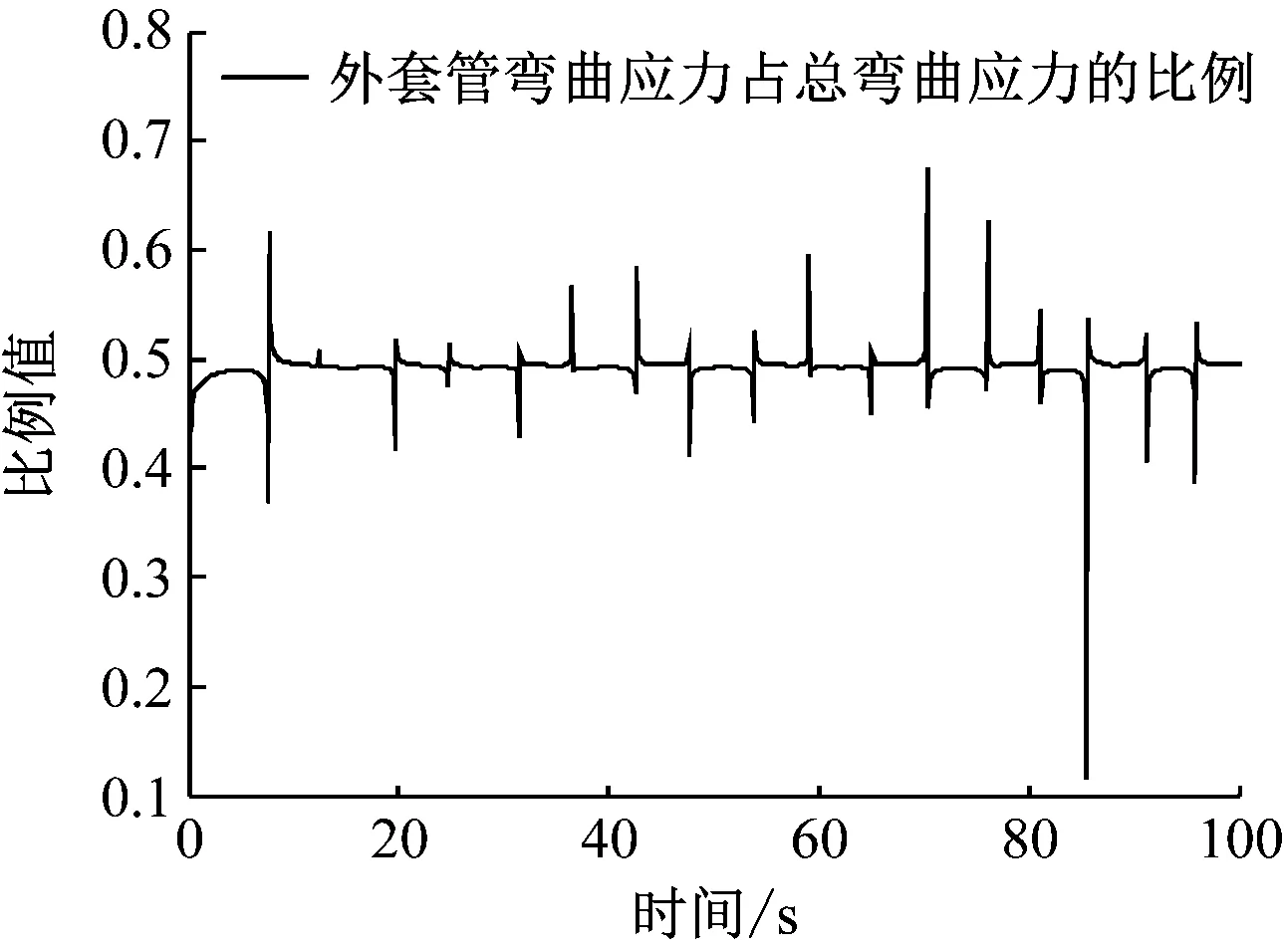
图16 外套管弯曲应力与总弯曲应力的比值时程图
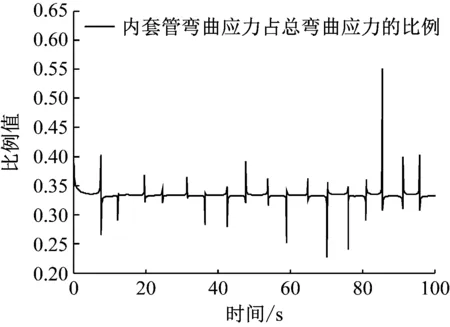
图17 内套管弯曲应力与总弯曲应力的比值时程图
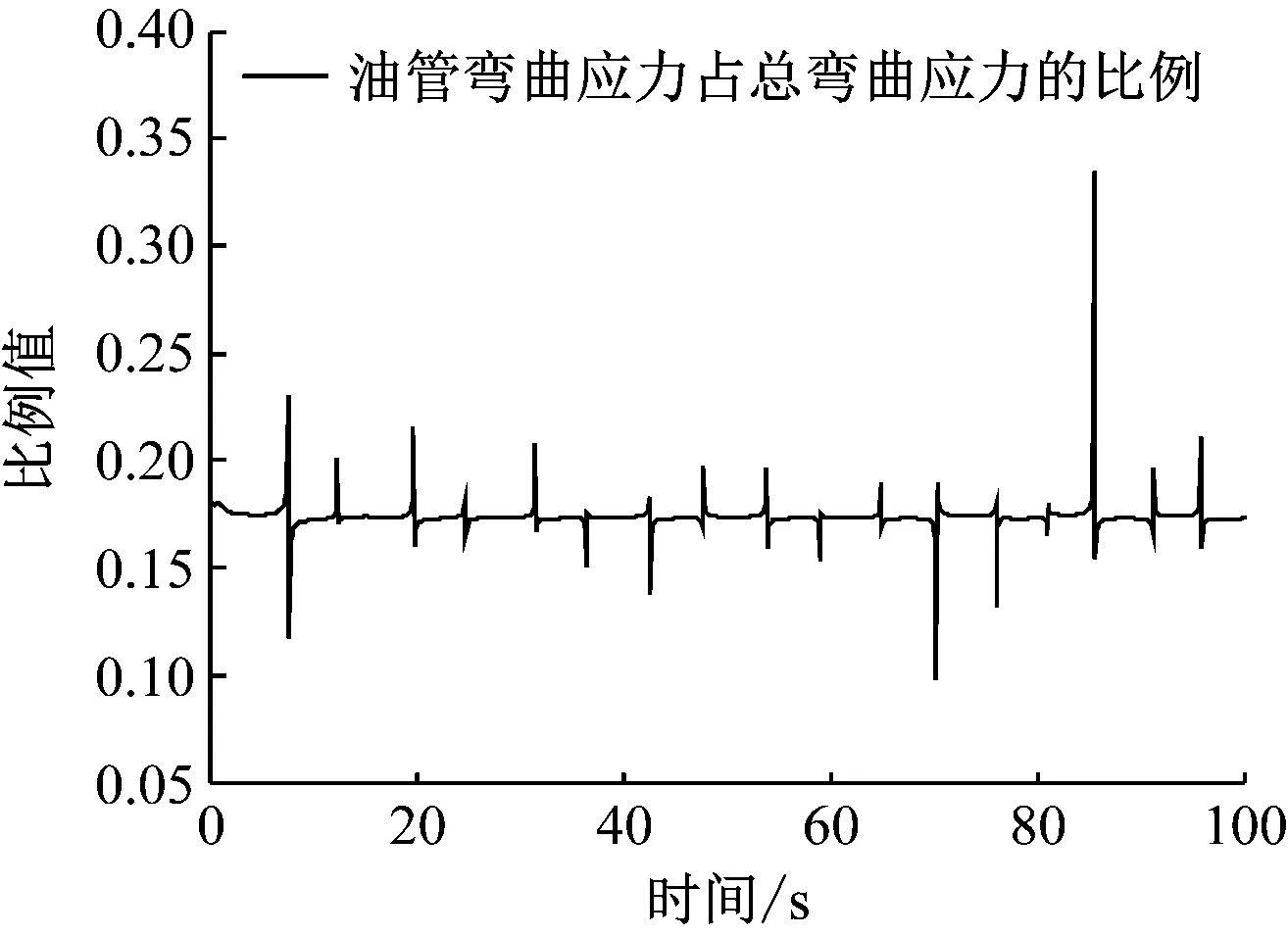
图18 油管弯曲应力与总弯曲应力的比值时程图
从图15中可看出,各层立管85 m节点处所受弯曲应力具有随机性,外套管所受弯曲应力最大,内套管次之,油管最小,这是因为外套管直接承受环境载荷,起到保护内管的作用,而内套管和油管仅受扶正器处相互作用力的作用,扶正器产生的相互作用力属于被动力。
从图16中可看出,外套管所受弯曲应力与总弯曲应力的比值在0.506附近波动;从图17中可看出,内套管所受弯曲应力与总弯曲应力的比值在0.332附近波动;从图18中可看出,油管所受弯曲应力占总弯曲应力的比值在0.175附近波动;根据弯曲刚度等效分配原理分别求出内套管、外套管和油管的弯曲刚度占比分别为0.772 7、0.207 5和0.019 8。
上述分析结果显示,将弯曲应力按弯曲刚度之比分配所得结果与实际计算的结果不符,理论值会高估外管承受的弯曲应力,会低估内套管和油管承受的弯曲应力。因此,在实际设计立管过程中,应根据耦合立管模型的计算结果对各层立管进行强度校核。
4 结 语
本文在文献[1]的基础上,对深水顶张式立管分析模型进行了改进。一方面,考虑了上部平台运动对立管运动响应的影响;另一方面,对立管管间间隙在计算方程中的处理方式进行了讨论。通过对深水顶张式立管的运动响应和弯曲应力进行分析,主要得出以下结论:
1)在分析顶张式立管时,不能忽视扶正器和管间间隙对立管运动响应的影响,扶正器的几何参数、布置间距和管间间隙都会对立管耦合运动产生重要影响。与等效立管模型相比,顶张式立管耦合模型能更好地模拟实际立管模型。在对顶张式立管进行动力学研究时,应充分考虑上部平台的影响。
2)通过对耦合立管的弯曲应力进行分析发现,将弯曲应力按弯曲刚度之比分配所得结果与实际计算的结果不符,理论值会高估外套管承受的弯曲应力,会低估内套管与油管承受的弯曲应力。因此,在实际设计立管过程中,应根据耦合立管模型的计算结果对各层立管进行强度校核,对今后的立管设计有一定的参考意义。

