尾流干涉下立管涡激振动试验研究*

赵德光 娄敏 王晓凯 张睿

(1.中国石油大学(华东)石油工程学院 2.海洋石油工程(青岛)有限公司)

0 引 言

涡激振动是一种广泛存在于自然界中的流固耦合现象，海水流经立管时会在尾流区内产生交替的漩涡，当漩涡脱落频率接近立管自振频率时会发生“锁定”现象，从而导致结构发生涡激振动现象[1-2]，进而缩短立管寿命[3]。

目前，国内外学者针对涡激振动问题进行了广泛研究。在数值求解方面，CUI Z.D.等[4]采用有限元法对并联排列的弹性耦合圆柱体涡激振动开展研究，发现两个圆柱的主频率在“锁定”状态内、外始终保持一致。M.RAHMANIAN等[5]对两个不同直径并联排列圆柱体的涡激振动进行研究，两圆柱仅考虑横流向振动，结果表明，小圆柱体的存在对大圆柱体的漩涡脱落方式和振动幅值产生了较大影响。王晓凯等[6]对串联排列圆柱的干涉效应进行研究，发现间距比和约化速度对下游圆柱的振动响应有显著影响。R.C.MYSA等[7]在低雷诺数下对串联排列圆柱的流动诱导振动进行研究，分析了升力组成中压力和黏滞力的意义以及与流速的关系。FAN X.T.等[8]研究了不同间距比下，串联排列三圆柱在亚临界雷诺数下的涡激振动模式，发现位移峰值是涡激振动与尾流激振共同作用的结果。武磊等[9]基于Open FOAM求解器，对阶梯流中不同浸没长度下的串联排列双立管涡激振动展开研究，发现随着浸没长度的增加，下游立管的漩涡泄放受上游立管的尾流作用得到进一步加强。在试验研究方面，G.R.S.ASSI[10-11]对两自由度串联、交错排列的圆柱体尾流诱导振动进行了试验研究，结果表明，当下游圆柱的初始位置从尾迹中心线向两侧偏离时，由诱导振动引起的激振效果会减弱。S.W.KIM等[12]在亚临界雷诺数范围内，研究了柔性圆柱双自由度的耦合运动，采用三维位移计和张力计测量模型的动态响应，并将得到的响应幅值和漩涡脱落频率与他人的试验结果进行对比分析。HU Z.M.等[13]利用风洞试验研究了不同质量-阻尼比下单自由度串联排列圆柱的流动诱导振动特性，结果表明，随着质量-阻尼比的增大，两圆柱的无量纲振幅、振动区域与滞后现象等所受影响将逐渐减小。梁文洲[14]系统地对串列排列、并列排列和交错排列的双圆柱体开展试验研究，得到了有别于单圆柱体和固定不动双圆柱体或双圆柱体单自由度涡激振动的变化规律。在涡激振动抑制方面，娄敏等[15]采用有限元软件分析了不同约化速度下，仙人掌形截面对柔性圆柱体的抑振效果。刘志慧等[16]对具有盘球附体的立管模型进行抑涡试验，发现螺距是影响盘球附体抑涡效果的重要因素。娄敏等[17]对带三控制杆的串联立管进行试验，分析了不同立管间距对三控制杆涡激振动抑制效果的影响。宋振华等[18]研究了3根附属杆抑制装置对立管的抑制效果及抑制机理，发现间隙比和来流角度对立管的抑制效果有显著影响。

目前在求解立管的涡激振动问题上，二维数值模拟采用的质量-弹簧-阻尼系统忽略了立管非线性运动响应，难以适用于刚度较小且构型复杂的柔性立管[19]。受限于计算成本，采用有限元求解三维顶张力立管和悬链线立管的涡激振动问题尚不成熟。在此背景下，本文在室内波流联合水槽中分别开展刚性立管和柔性立管涡激振动试验，选取不同材质模型用于模拟实际工程中的刚性立管与柔性立管(顶张力立管和悬链线立管)，并通过试验得到立管模型在不同排列方式下的响应特性随来流速度的变化关系，对比分析不同工况下流动干涉效应，以期为进一步研究尾流干涉下海洋立管涡激振动提供参考。

1 试验目的及方法

为深入探究刚性立管和柔性立管在不同排列方式下的响应特性随来流速度的变化关系，以及上游立管对下游立管尾流干涉的影响规律，本文于2021年3月采用模型试验的方法对立管进行动力响应分析。

1.1 试验器材

试验水槽为中国石油大学(华东)室内波流联合水槽，水槽尺寸为16.0 m(长)×0.8 m(宽)×1.4 m(高)。该水槽能够造出指定波高和周期的规则波与不规则波，同时可以双向造流，可产生0.05～0.70 m/s的来流速度。

试验用管材料分别为硅胶管和有机玻璃管(Polymethyl methacrylate，PMMA)。硅胶管质地较为柔软，在室内水槽的小尺度条件下能够随水流自由运动，呈现应有的构型，主要用于柔性立管的试验；PMMA管又叫亚克力管，综合力学性能较好、机械强度较高，可用于刚性圆柱的模型试验。本次试验中选取的立管模型有效长度(1.5 m)、外径(10 mm)和壁厚(2 mm)等参数均保持一致，其他物理特性参数存在一定差异，具体如表1所示。

表1 材质参数Table 1 Material parameters

根据水槽尺寸定制铝合金支架、插槽、插块结构，以实现水槽在无需放水的情况下快速更换立管模型，提高试验效率。由于铝合金支架的刚度整体较大，在来流作用下支架与立管模型不会发生共振作用。为与实际工程中立管的运动状况相符，本次试验按照立管模型参数定做了柔性接头，模型两端采用万向节进行连接，保证其在任意方向上的运动不受阻碍。

为捕获立管的振动响应，采用非接触位移测量仪(3D-PDT精密位移测量仪)和光纤光栅测试系统两种不同方式进行测量。其中，非接触位移测量凭借两个分辨率为500万像素的高清摄像头对物体表面的标记测点进行实时捕捉(不会对流场造成影响)，可在立管模型上自由布置测点，方便对任意位置处的响应进行监测。光纤光栅测试系统由布拉格光纤光栅传感器(Fiber Bragg Grating sensors，FBG)和光纤光栅解调仪两部分组成。FBG体积微小，相比于其他测试仪器对外部流场和结构本身都不会产生明显影响，当传感器数目较多时还可以采用焊接的方式将光纤串联在一起，有效避免传统电阻应变片单个单线导致的线路冗杂。

1.2 试验步骤

试验开始前，使用白色有机硅密封胶对立管模型的下端进行密封处理，目的是能够向管内注入流体以增大附加质量，适当降低自振频率。使用PMMA管进行刚性立管的模型试验，对立管模型布置光栅应变测点和非接触测点，每种测量仪器所对应的测点个数和测点位置如图1所示。使用硅胶管进行柔性立管的模型试验，顶张力立管模型与悬链线立管模型的构型如图2所示。与刚性立管模型的非接触测点布置情况一致，从模型的中部开始布置非接触测点，从上到下依次为测点1、测点2和测点3。将立管模型安装在铝合金支架后垂直放置于水槽中，浸没深度为750 mm。

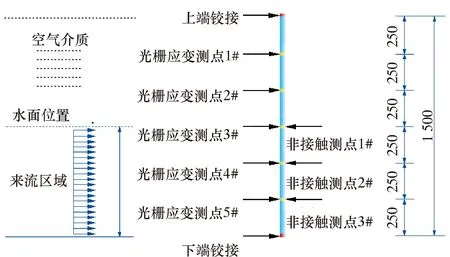
图1 立管模型测点布置示意图Fig.1 Layout of measuring points on riser model

图2 立管模型Fig.2 Riser model

试验期间对水槽造流机产生的实际流速进行测试校准。在波流水槽内安装声学多普勒流速仪，对试验过程中的来流流速进行实时监测。为保证试验结果的准确性，在后续试验中所采用的流速皆以校核后的实际流速为准。

将材质为PMMA的刚性立管模型内部注满流体后放置于水槽中，通过敲击试验测定立管模型的自振频率，通过非接触摄像机测得的自振频率fn1=2.52 Hz，通过光纤光栅系统测得的自振频率fn2=2.44 Hz，两者在数值上较为接近，确保了测试结果的准确性及可靠性。考虑柔性立管的特殊构型及运动情况，采用非接触位移测量仪实时记录立管模型的振动特性，通过敲击试验测量柔性立管的自振频率为1.85 Hz。

2 试验内容

为探究刚性立管和柔性立管尾流干涉下的涡激振动特性，本文分别进行刚性孤立立管试验、刚性立管尾流干涉试验、柔性孤立立管试验和柔性串联立管尾流干涉试验。

在刚性立管模型尾流干涉试验中，两根立管保持固定间距比，即S/D=5，并采用串联排列、交错排列与并联排列3种排列方式。图3为不同排列方式下的双立管模型。图3中α表示来流方向与两立管轴向中心连线之间的夹角，即来流角度的大小取决于两立管模型的相对位置，3种不同的排列方式对应来角度分别为0°、45°和90°。本文重点关注来流角度的改变对两立管模型之间流动干涉效应的影响。图3中D为立管直径，z轴垂于xy平面，表示立管模型上某点的高度坐标，u为来流流速。

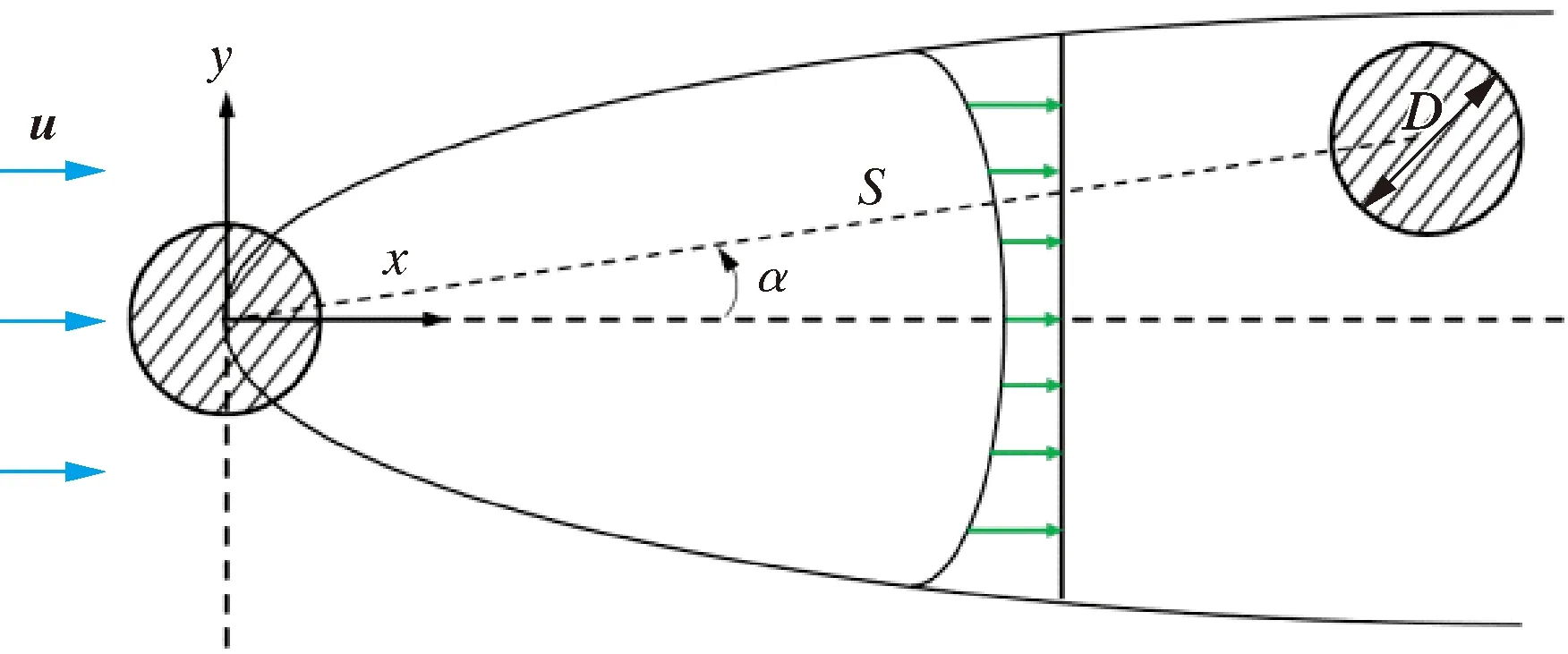
图3 双立管排布示意图Fig.3 Schematic diagram of double riser arrangement

在柔性立管模型尾流干涉试验中，两根立管保持间距比S/D=5并采用串联排列方式，其中顶张力立管处于上游位置，悬链线立管模型布置在下游位置，测点设置与前文保持一致。

3 试验结果及分析

3.1 刚性孤立立管试验分析

当漩涡脱落频率(fs)与固有频率(fn)的比值趋于相近时立管模型便处于“锁定”状态。图4表示不同约化速度(Vr=u/(fnD))下立管模型的频率比。由图4可得，非接触摄像机与光纤光栅系统的测试结果非常接近，频率比随约化速度的增大在数值上相应增加。根据定义可判断立管模型的“锁定”区间为Vr=5～9。

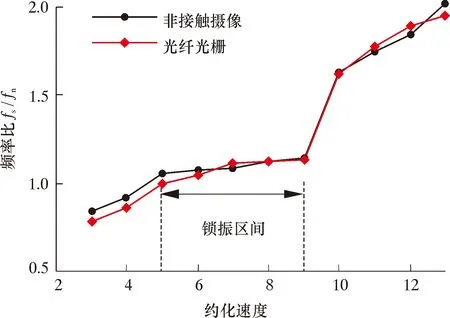
图4 频率比Fig.4 Frequency ratio

重点关注立管模型中间位置,即非接触测点1处响应特性，立管模型在两个流向上的幅值(以y/D或x/D来表示)如图5所示。横流向振幅(y/D)在“锁定”区间内显著增加，当Vr=6时取得最大值，约为0.46。离开“锁定”区间后幅值迅速下降。顺流向幅值随来流速度的增加呈上升趋势。观察发现，两种不同采集仪器得到的结果较为接近，再次印证了试验结果的准确性。

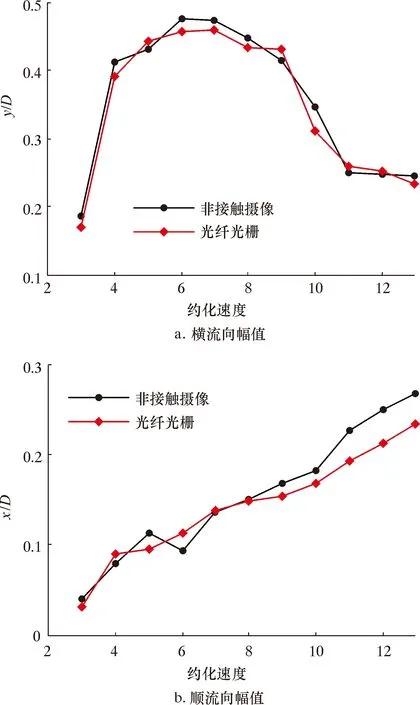
图5 立管模型振动幅值曲线Fig.5 Vibration amplitude curve of riser model

图6为处理后得到的立管模型位移(以相对位置来表示，即z/L)包络图。图6中不同颜色的曲线代表立管模型在来流作用时间内不同时刻所处的振动位置，L表示立管模型的长度。

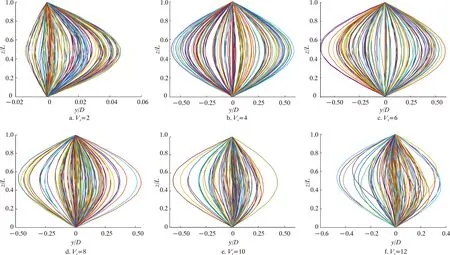
图6 立管模型位移包络图Fig.6 Displacement envelope diagram of riser model

观察发现振动幅值沿管长方向呈现出两端小、中间大的分布特征，最大值出现在立管模型中部位置，同时在“锁定”区间内运动幅值明显增加，与图5中呈现的结果相符。此外，随着来流速度的不断增大，立管模型承受的激励作用不断提升，在图6f中可以观察到2阶振型的出现，标志着振型由此发生转变。

3.2 刚性立管尾流干涉试验分析

不同来流角度时下游立管受干涉作用后的响应特性变化情况如图7与图8所示。图7表示频率比的变化情况。受上游立管模型流动干涉效应的影响，下游立管模型的频率比与孤立立管相比发生了显著变化。观察发现，当α=0°时下游立管模型的“锁定”区间为Vr=6～10，与孤立立管Vr=5～9相比存在一定滞后，原因在于上游立管的流动干涉效应导致流经下游立管的实际来流速度小于设定流速，因此“锁定”区间将向后推移发生在较大Vr处，同时频率比在数值上将小于孤立立管；而当α=45°和90°时，下游立管模型的频率比在数值上与α=0°相比逐渐增大，同时“锁定”区间的范围与孤立立管保持一致，由此判定α=0°即串联排列时下游立管所受流动干涉效应最为显著，随着来流角度的增大干涉作用逐步减弱。

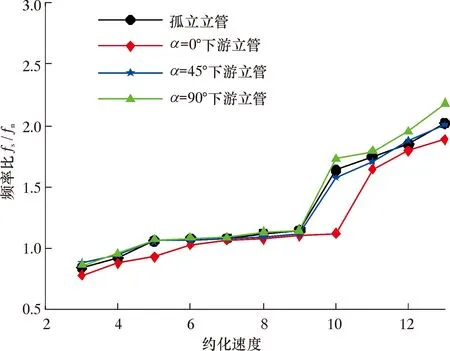
图7 不同来流角度下频率比Fig.7 Frequency ratio in different inflow angles

图8表示不同来流角度时下游立管模型无量纲振幅随Vr的变化关系。由图8可得，当α=0°时，高约化速度时下游立管模型的横流向振幅(y/D)相比孤立立管明显提升，原因在于上游立管模型的流动干涉效应引发了流体与下游立管模型间更剧烈的非线性相互作用，致使其振动幅值明显大于孤立立管，随来流角度的增大横流向振幅逐渐降低，愈发接近于孤立立管；受上游立管模型流动干涉的影响，α=0°时下游立管模型的顺流向振幅(x/D)小于孤立立管，随着来流角度的增大干涉效应逐渐减弱，顺流向振幅相应增加并在数值上逐渐超过孤立立管。

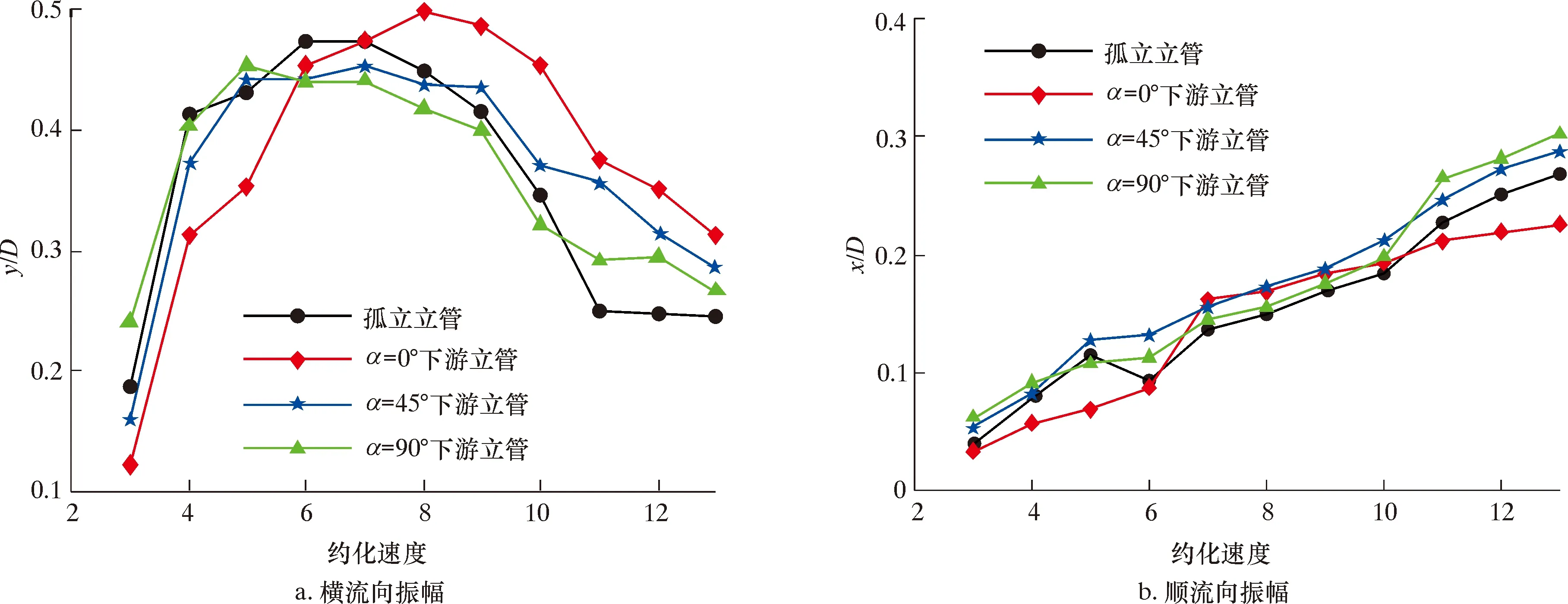
图8 不同来流角度下的振幅曲线Fig.8 Amplitude curve in different inflow angles

3.3 柔性孤立立管试验研究

图9表示柔性孤立立管模型在不同Vr下的横流向振动幅值。观察发现：柔性顶张力立管模型的响应幅值变化与刚性立管较为相似，开始阶段振动幅值较小、增长缓慢，进入“锁定”区间后迅速增大并趋于平稳，离开“锁定”区间后振幅随之下降，同时立管中部的幅值最大；悬链线立管模型则有所不同，主要原因在于其独特构型导致多阶振动模态的同时存在，使得在同一来流速度下不同测点处的振动幅值差异显著。

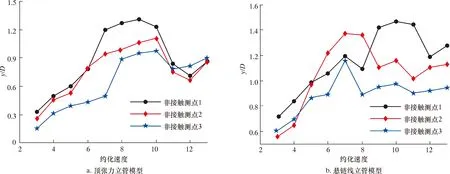
图9 柔性孤立立管模型振动幅值Fig.9 Vibration amplitude of flexible riser model

3.4 柔性串联立管尾流干涉试验研究

在柔性立管尾流干涉试验中，下游悬链线立管模型受流动干涉作用后的振动幅值与孤立悬链线立管的对比情况如图10所示。

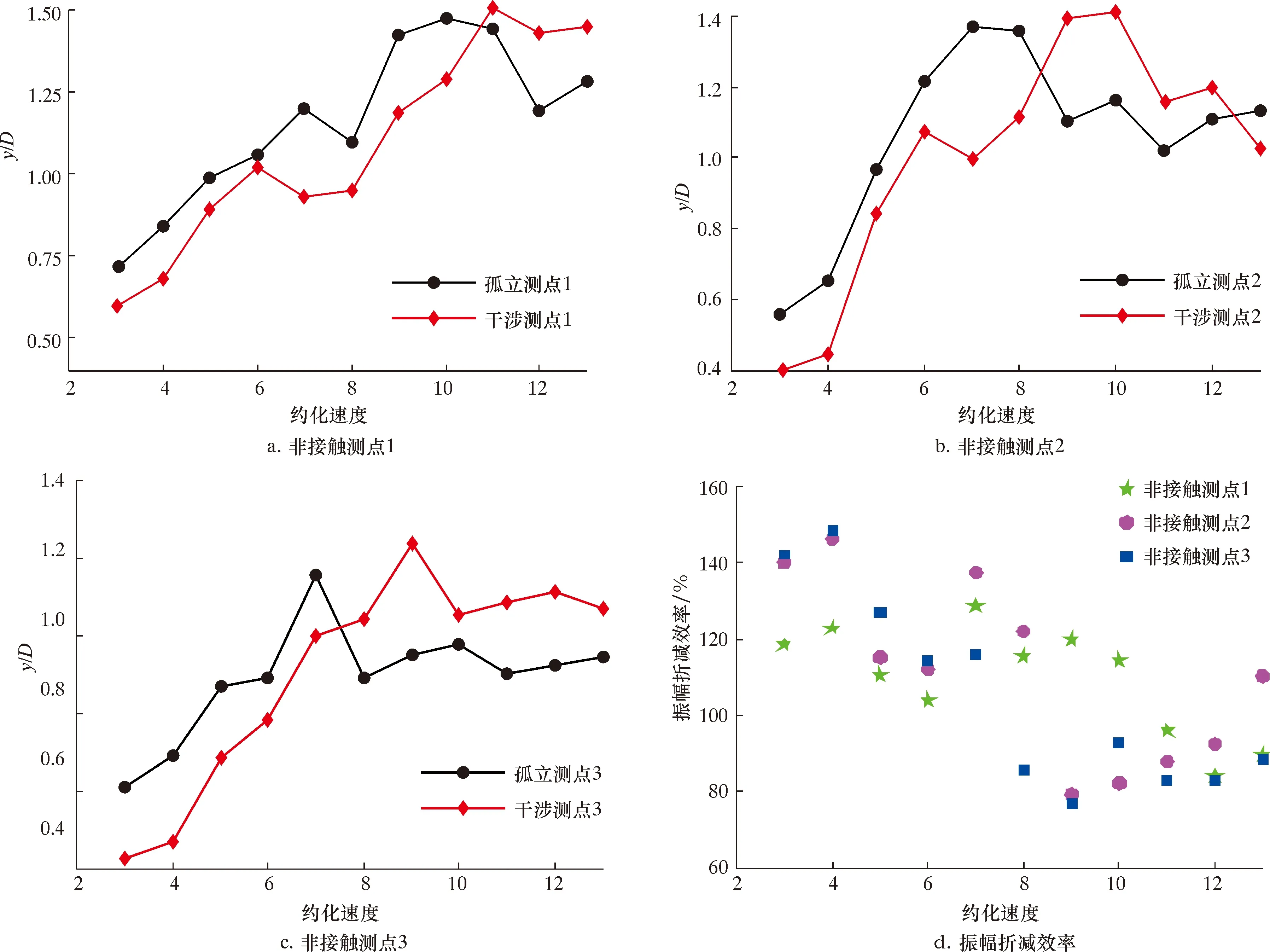
图10 悬链线立管模型振幅对比Fig.10 Amplitude comparison of catenary riser model

本文引入振幅折减效率η，以此表征干涉作用前、后悬链线立管模型振幅的变化情况，如式(1)所示。

(1)

式中：η表示振幅折减效率，yRMS表示孤立悬链线立管模型的横流向振动幅值，yDRMS表示串联排列下游悬链线立管模型的横流向振动幅值。

η越接近于100%，表示干涉前、后悬链线立管模型的振幅差异越小，即说明下游悬链线立管模型受到的干涉效应影响相对越弱。由图10d综合分析可得，下游悬链线立管模型非接触测点1处所受干涉影响最弱，非接触测点3处所受干涉影响最强。分析原因主要在于悬链线立管构型独特，不同截面所处的垂向位置存在一定偏差，下游悬链线立管模型从上端到下端与上游顶张力立管模型的水平间距逐渐减小，间距越小即受到的流动干涉效应随之越强，因此从非接触测点1到非接触测点3所受的干涉作用逐渐增强。

4 结 论

(1)孤立刚性立管模型的“锁定”区间为Vr=5～9，在此区间内流体与立管间产生剧烈的非线性相互作用，立管在横流向持续以较大幅度振动，顺流向振幅随着约化速度的增大持续增大；立管横流向振动幅值沿管长方向呈现出两端小、中间大的分布特征，约化速度为12时可观察到2阶振型的出现。

(2)在刚性立管尾流干涉试验中，来流角度对下游立管模型的流动干涉作用有显著影响。当α=0°时，下游立管模型的“锁定”区间相比孤立立管有一定滞后，在高约化速度下，下游立管横流向振幅有所增大，受干涉作用影响顺流向振幅小于孤立立管；随着来流角度的不断增大，下游立管所受流动干涉作用逐步减弱，横流向振幅逐渐降低并接近于孤立立管，顺流向振幅相应提升并在数值上逐渐大于孤立立管。

(3)柔性孤立顶张力立管的振动特性与刚性立管相似，而孤立悬链线立管模型由于构型独特，导致在来流作用下多阶振动模态共存，不同测点处的横流向振动幅值差异相对较大。

(4)在柔性串联立管尾流干涉试验中，受上游顶张力立管流动干涉影响，下游悬链线立管的响应幅值与柔性孤立立管相比存在较大区别。由振幅折减效率分析可知，下游悬链线立管从非接触测点1到非接触测点3所受的干涉影响逐渐加强，即与上游立管水平间距越小的位置受到的流动干涉效应越强。