基于ROS 的PID 闭环控制仿真实验设计
王庆,黎文娜
(南京师范大学 泰州学院信息工程学院,江苏泰州,225300)
0 引言
近年来,随着机器人应用需求越来越大,越来越多的高校开设了机器人的相关课程乃至成立了机器人的专业,机器人技术是一门交叉性的学科,培养掌握机器人技术的应用型本科人才需要更多创新性的教学思维和实验方法。ROS(Robot Operating System)是一个适用于机器人的开源的操作系统,它提供了操作系统应有的服务[1],在机器人控制当中,PID 算法凭借着简单、高效,易实现等特点依然有着很强的生命力,是本科生需要掌握的控制算法。本实验在ROS 环境下利用turtlesim 仿真器模拟一个根据指令移动到指定地点的过程,对于运行中出现的误差,使用比例、积分以及微分控制予以补偿,使得仿真器中的小海龟到达指定点位,并分析三种控制在仿真状态下各自的优缺点以及对最终结果的影响。
1 PID 闭环控制原理
PID 控制算法是一种具有几十年历史的经典控制算法,在工业控制中已经得到了广泛的应用,该算法是控制算法中最经典、最简单、而又最能体现反馈控制思想的算法[2],在机器人控制领域该算法依然发挥着不可替代的作用,PID 算法的执行流程是非常简单的,即利用反馈来检测偏差信号,并通过偏差信号来控制被控量,而控制器本身就是比例、积分、微分三个环节的相加和。其原理如图1 所示。

图1 基本PID 控制算法原理图
根据图1 我们考虑在某个特定的时刻t,此时输入量为rin(t),输出量为rout(t),于是偏差就可计算为err(t)=rin(t)-rout(t)。于是PID 的基本控制规律就可以表示为如下公式:

其中kp为比例带,TI为积分时间,TD为微分时间,比例就是用来对系统的偏差进行反应,所以只要存在偏差,比例就会起作用。积分主要是用来消除稳态误差,所谓稳态误差就是指系统稳定后输入输出之间依然存在的差值,而积分就是通过偏差的累计来抵消系统的稳态误差。而微分则是对偏差的变化趋势做出反应,根据偏差的变化趋势实现超前调节,提高反应速度。当在计算机上实现PID 算法时,就必须要将其离散化,假设系统采样周期为T0,在检查第K个采样周期,很显然系统进行第K 次采样。此时的偏差可以表示为err(k)=rin(k)-rout(k),那么积分就可以表示为:err(k)+err(k+1)+……,而微分就可以表示为:(err(k)-err(k-1))/T0,于是可以将第k次采样时,PID 算法的离散形式表示为:

也可以进一步表示为:

2 仿真实验设计原理
本实验是基于ROS 环境下的turtlesim 仿真器运行的,ROS 下的通讯机制常用的有两种话题(Topic)与服务(Service),由于有些情况下不需要周期性的获得一些数据,只想在离散的时间点获得数据,这样的情况下,topic 这种单方向的频繁发布消息的通讯模式就显得不那么适用了,这时,这种一问一答的模式就非常好用了,当需要数据的时候来一个请求就可以了,Service 与 topic 最大的不同是,它是双向通信,一方发布请求查询等待结果,一方执行,并反馈结果;因此服务分为客户端请求,和服务端反馈。Service 是同步通讯机制,当客户端发送一个请求后,服务端几乎同时做出响应,等待响应完成后,服务端才反馈结果给客户端;而在客户端在等待反馈的过程中一直处于阻塞的状态,直到接受到反馈后,客户端才会执行接下来的动作。这样的一种通讯形式的特点是离散,高效,指向性强,不会出现类似话题的形式,一直发布消息大量占用资源,显然,本实验更适合采取Service 通讯机制来完成,Service 通讯图如图2 所示。

图2 Service 通讯图
3 实验开发环境及软件流程
本实验的系统环境为ubuntu20.04,ROS 的版本为noetic,开发环境为Visual Stdio Code,仿真器为ROS 自带的turtlesim。
实验设计的总体思路为:在ROS 的运行机制下,客户端首先发布点位请求,服务端收到请求后,进入服务端的函数,服务端通过PID 算法在设定频率下不断的发布控制小乌龟的角速度和线速度的话题给乌龟节点,乌龟运动,同时乌龟也会同时发布自己的位置的话题,当乌龟动作完成后,服务端给客户端反馈结果[3]。turtlesim 节点是每个在安装ROS 包的时候就已经在电脑上的,使用时直接调用就可以了,在这个实验中我们需要在服务器节点将PID 控制算法实现,在终端直接call 服务即可,从而完成实验。
■3.1 实验流程
(1)创建功能包turtle2pose。
(2)创建源文件turtleControl.cpp。
(3)编写服务端PID 闭环控制算法。
(4)创建并定义 srv 文件。
(5)创建 launch 文件。
(6)CMakeLists 修改。
(7)运行launch 文件,使用rosservice 命令发送目标坐标,通过观察turtlesim 仿真器及plotjuggler 软件分析比例、积分、微分控制对实验结果的影响。
本实验采用C++语言编程实现控制算法,仿真器频率设置为50Hz,小乌龟需要根据命令从一个点运动到另一个点,需要两个运动步骤转角和前进,转角控制了移动的方向,前进控制了移动的距离,如图3 所示,小乌龟初始点为原点,坐标为(0,0),要控制小乌龟移动到具体的点,就是要解决转向和前进的问题。

图3 turtlesim 仿真器
■3.2 转角
小乌龟当前的坐标和角度可以通过订阅/turtle1/pose话题获得相关的信息,当前角度为pose_z,根据命令中发布的坐标req.x、req.y,通过三角函数atan2(req.y,req.x)可得需要转角的目标值msg_aim.data,如果直接让小乌龟以固定速度转角度,显然速度越大,转角的误差越大,不够稳定,存在误差,因此需要PID 控制,让小乌龟以合适的速度转到目标角度,目标值与当前值之间存在误差msg_error.data=msg_aim.data-pose_z,将误差与合适的系数进行运算转换为合适的角速度输出用于调节当前角度值pose_z,v.angular.z=kp·msg_error.data+ki·msg_error_i.data+kd·msg_error_d.data,使之无限接近于目标值msg_aim.data。
■3.3 前进
为了使小乌龟前进的距离准确,同样需要用到PID 算法进行控制,整体的思路与转角的方法相似,在程序具体编写的时候相关的变量都可以复用,首先要算出当前点与目标点的距离即误差msg_error.data=msg_aim_line.data-sqrt(pow(pose_x-pose_x_start,2)+pow(pose_y-pose_y_start,2)),只需要将误差进行PID 运算后产生的速度的值赋给线速度,用于调节当前小乌龟的位置,v.linear.x=kp·msg_error.data+ki·msg_error_i.data+kd·msg_error_d.data,使之无限接近于目标msg_aim.data。
■3.4 实验步骤及现象分析
步骤一:对写好的功能包使用catkin_make 命令进行编译。
步骤二:分别对kp,ki,kd进行取值,取不同的值,本实验目标点坐标取(3,3),当误差小于0.0001 则认为小乌龟到达设定目标,则跳出程序,在终端中输出所需时间以及service(服务)的反馈,通过plotjuggler 观察分析误差与目标的曲线,并观察仿真器中小乌龟的运动状态,分析不同的取值对实验结果的影响。
比例调节:比例调节即p 调节,在程序中首先设置ki与kd为0,kp分别取值0.2、2、20,编译程序后启动turtlesim仿真器,利用rosservice 命令发布目标点坐标,观察转角目标/aim/data 以及仿真器中小乌龟当前位置/turtle1/pose/theta 两个话题以及直行目标/aim_line/data 与当前已直行距离/pose_value_now/data 两个话题的曲线如图4~图7 所示。

图4 不同系数下的p 调节转角
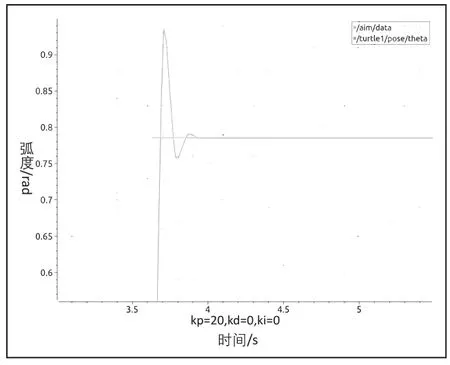
图5 不同系数下的p 调节转角

图6 不同系数下的p 调节直行

图7 不同系数下的p 调节直行
现象分析:比例调节在于成比例的调节误差,通过上图可以看到,当小乌龟开始向目标角度转动以及直行时误差一旦出现立即产生作用减小误差,不断的成比例线性的向目标靠拢,在整个曲线趋于稳定时会发现存在着误差无法消除,这种误差称之为稳态误差,在比例调节中只有误差存在,才会有速度产生,所以比例调节必然会有误差存在。稳态误差在仿真器中的现实意义则是越靠近目标,误差越小,速度越小,当速度无法使小乌龟运动时则就停了下来,误差则一直存在,即为稳态误差。比例系数kp越小,产生的速度越小,小乌龟运动的越慢,到达稳定的时间越长,反之,比例系数kp越大,产生的速度越大,小乌龟运动的越快,到达稳定的时间越短。但kp并不是越大越好,过大会使仿真器中小乌龟快速的晃动或者转圈,在曲线图上反应出来的就是较大的超调和振荡,导致小乌龟不稳定,因此,不能将kp选取过大,应根据实际发布的目标点的坐标选取合适的比例系数kp,使得稳态误差控制在合适的范围内,同时又具有较快的响应时间。
积分调节:积分调节即i 调节,在程序中设置kp=0.2,ki=0.1,kd=0,设置积分的区间,当误差小于0.5 时,积分调节介入,否则积分过大会造成整个系统的超调和振荡,编译程序后启动turtlesim 仿真器,利用rosservice 命令发布目标点坐标,观察转角目标/aim/data 以及仿真器中小乌龟当前位置/turtle1/pose/theta 两个话题以及直行目标/aim_line/data 与当前已直行距离/pose_value_now/data两个话题的曲线如图8、图9 所示。

图8 i 调节转角

图9 i 调节直行
现象分析:积分调节主要用来消除稳态误差,只要误差存在,积分环节就会起作用,本实验中,在50Hz 的频率下对当前误差进行不断的累计,使得小乌龟的速度不断变化,产生作用来减小误差,经过一定时间后如图所示,位置曲线是收敛的,误差消除。
微分调节:微分调节即d 调节,在程序中首先设置ki与kd为0,kp分别取值0.5、2、20,编译程序后启动turtlesim 仿真器,利用rosservice 命令发布目标点坐标,观察转角目标/aim/data 以及仿真器中小乌龟当前位置/turtle1/pose/theta 两个话题以及直行目标/aim_line/data与当前已直行距离/pose_value_now/data 两个话题的曲线如图10~图13 所示。

图10 不同系数下的d 调节转角
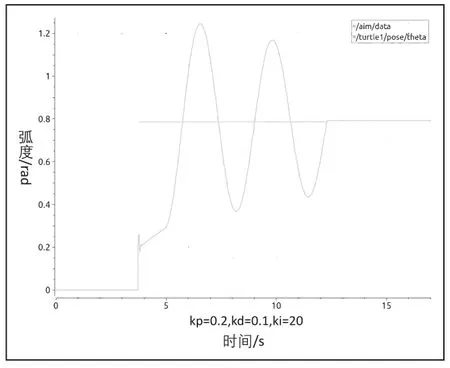
图11 不同系数下的d 调节转角
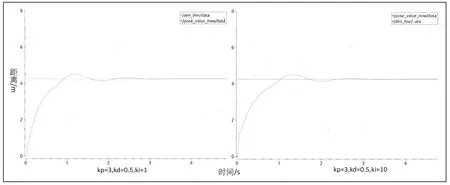
图12 不同系数下的d 调节直行
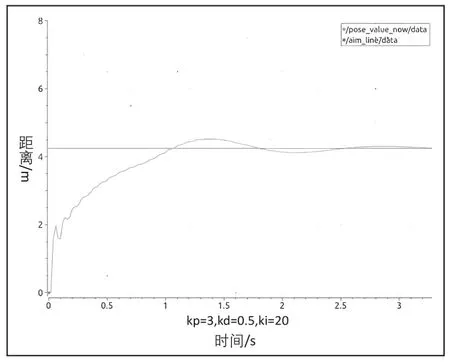
图13 不同系数下的d 调节直行
现象分析:微分调节能够反映误差的变化趋势,当误差的变化变得太大之前,引入一个有效的早期修正信号,从而加快到达目标的动作速度,减小调节时间,在积分调节中,虽说可以消除稳态误差,但到达目标的时间也被拉长并且会产生超调和震荡,这时候微分调节的介入,在误差刚出现的瞬间,不仅能够根据比例积分的控制作用对误差作出及时反应,还能够根据误差的变化趋势(速度)通过微分调节提前给出较大的控制作用,将误差消灭在萌芽状态,微分环节让小乌龟运动时减小超调,克服振荡,加快转动速度,缩短达到目标的时间[4],结合曲线图,如表1、表2 所示,在kp与ki完全相同的情况下,随着kd的变大,到达目标的时间明显缩短。

表1 kd取不同值时小乌龟转角到达目标的时间

表2 kd取不同值时小乌龟直行到达目标的时间
4 结语
本实验主要涉及了ROS 机器人与PID 闭环控制算法两方面知识,利用ROS 自带的turtlesim 仿真器结合ROS 节点的service 机制对仿真器中的小乌龟实现PID 闭环控制作用,实现结果表明仿真器中小乌龟的运动轨迹及曲线符合PID 控制器特性。学生通过本实验不但可以了解ROS 的运行机制,理解最重要的话题与服务的区别并掌握他们的使用方法,而且对PID 闭环控制有了初步的理解,了解比例、积分、微分调节的意义,为后续PID 控制算法的学习打好基础。

