工程机械油气悬挂刚度特性研究
陈 俊,向 峰
(三一重工股份有限公司,湖南 湘潭 411100)
0 引言
油气悬挂是以惰性气体(氮气)作为弹性介,以油液作为传力介质,由蓄能器(相当于气体弹簧)和具有减振器功能的悬挂缸组成。与传统悬挂相比,油气悬挂具有典型的非线性弹性特性和良好的减振性能,因此,其拥有广阔的发展前景。目前,部分工程机械底盘采用了油气悬挂技术,其中悬挂油缸是悬挂系统的重要组成部件,所以对悬挂油缸进行数学建模及分析,对悬挂系统的油缸选型可以起到至关重要的作用。本文通过仿真与实验相结合来验证数学模型的正确性。
1 悬挂刚度特性
刚度特性是指活塞杆上所受到的弹性力(不包含阻尼力)与活塞相对于液压缸行程的关系,有静刚度特性和动刚度特性。刚度特性是油气悬挂的重要特性,直接影响到车辆行驶平顺性、悬挂动行程以及轮胎动载等。静刚度特性是指活塞杆相对于悬挂油缸缓慢移动时,活塞杆上所受到的力与活塞行程关系所决定的刚度特性;动刚度特性是指活塞杆相对于悬挂油缸快速移动,活塞杆上所受的力与活塞行程关系所决定的刚度特性。
缸体、活塞、活塞杆为悬挂油缸主要组成元件。其工作原理为:当活塞杆由缸体内伸出时,有杆腔和无杆腔之间产生压差,蓄能器向无杆腔补充液压油,有杆腔液压油流向另一个蓄能器,达到一个平衡状态。同样,当活塞杆缩进缸体时,有杆腔和无杆腔存在的压力差使无杆腔液压油流向蓄能器,而有杆腔内的液压油由蓄能器补充,达到活塞上下受力平衡。悬挂油缸在运动过程中产生的腔体内油液体积的变化,需要通过蓄能器的高压氮气体积压缩或膨胀来补偿,可以简易看作传统悬挂中的弹性元件。
2 数学模型
假设油缸的活塞杆产生位移x,悬挂油缸的工作原理如图1所示。有杆腔、无杆腔内压力为PA、PB,缸体内径横截面积分别为SA、SB。

图1 悬挂油缸的工作原理
以缸体为研究对象进行受力分析,活塞杆处于任意位置时的平衡方程式[1]如式(1)所示。
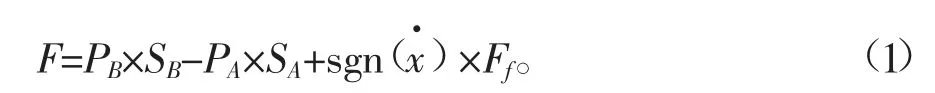
蓄能器1、2内的初始压力为P10=P20=P0,初始体积为V10=V20=V0。蓄能器内气体平衡位置时的压力和体积分别为:P′10,P′20,V′10,V′20。设油缸活塞从静平衡状态发生位移为x,则蓄能器的气体体积发生改变如式(2)、式(3)所示。

根据气体状态方程得到式(4)~式(6)。
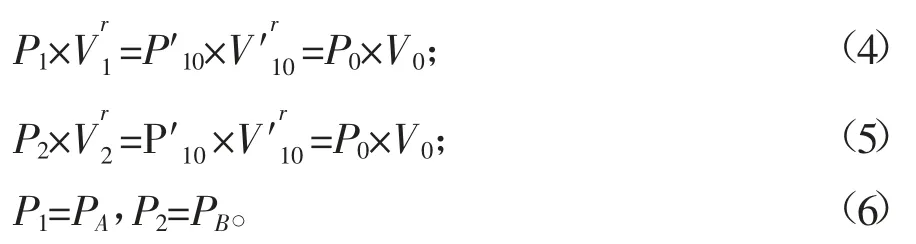
由式(1)~式(6)可得式(7)。

设悬挂支承的悬挂质量为M,静平衡状态蓄能器内的气体压力、体积如式(8)、式(9)所示。
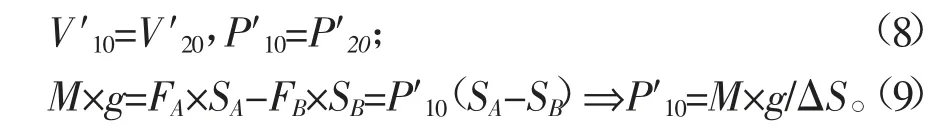
由式(1)~式(9)可得式(10)。

对x进行求导得式(11)。
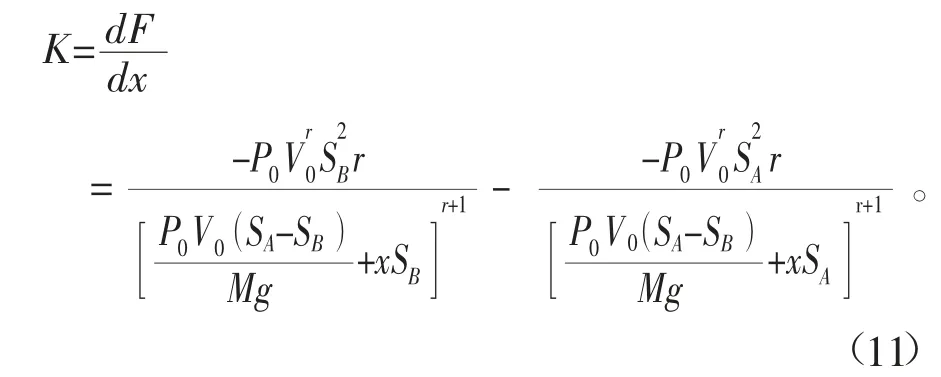
当x=0时,同时r=1即为静态刚度[2],可以得到式(12)。
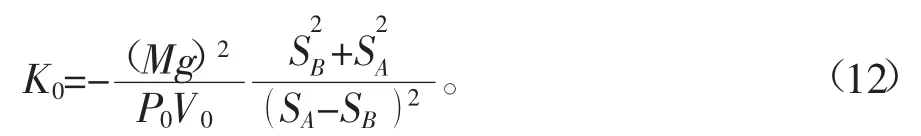
从式(11)和式(12)可以得出,影响悬挂刚度的参数有:初始气体体积与压力、输入信号、悬挂油缸有杆腔与无杆腔的截面积。气体多变指数的取值,当气体多变指数r=1时,气体为等温过程,此时可以得到油气悬挂系统的静刚度特性(缓慢加载过程可视为等温过程);当气体多变指数r=1.4时,气体为绝热过程,此时可以得到油气悬挂系统的动刚度特性,快速加载过程。但是,当悬挂油缸做缓慢动作的时候,可以看成是一个等温过程[3]。
3 仿真研究与试验验证
3.1 仿真研究
用MATLAB编程对油气悬挂数学模型进行仿真。蓄能器为初始状态时,P0=5.0 MPa,V0=2.8 L,蓄能器为静平衡状态时,Mg为一个常数。通过仿真试验得出关系曲线。
图2为x=0.05 sin(0.08πt)时的力与位移关系曲线(计摩擦力),该曲线考虑了油缸的摩擦力(摩擦力视为恒定值)。图3为x=0.05 sin(0.08πt)时的刚度系数与位移关系曲线。图4为x=0.1 sin(0.08πt)时的力与位移关系曲线(计摩擦力),图5为x=0.1 sin(0.08πt)时的刚度系数与位移关系曲线。从曲线可以看出,当加载位移发生变化时,悬挂刚度发生改变。当位移增大时,悬挂油缸的总作用力增大,悬挂的刚度也在增大,且悬挂的刚度特性反映了油缸压缩越大油缸的刚度系数越大。

图2 x=0.05 sin(0.08πt)时的力与位移关系曲线(计摩擦力)
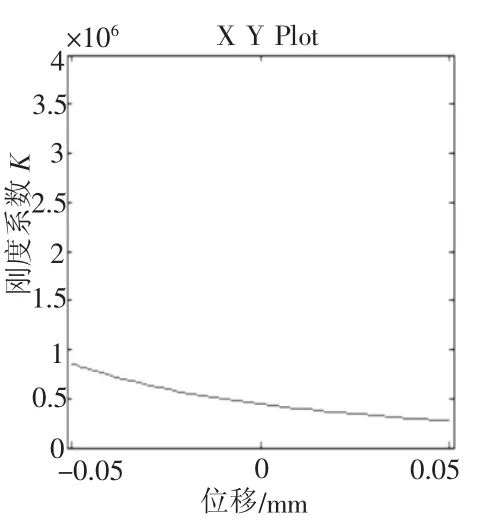
图3 x=0.05 sin(0.08πt)时的刚度系数与位移关系曲线
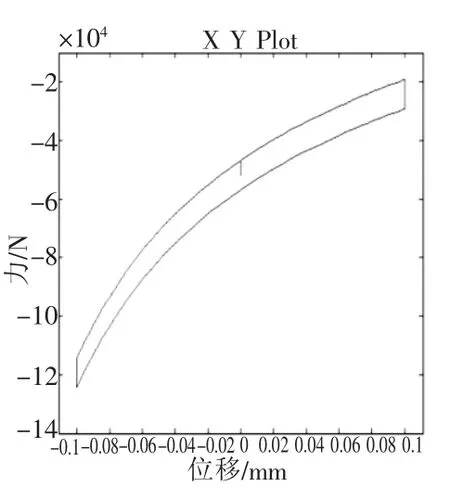
图4 x=0.1 sin(0.08πt)时的力与位移关系曲线(计摩擦力)

图5 x=0.1 sin(0.08πt)时的刚度系数与位移关系曲线
图6、图7分别为V0不变,x=0.1 sin(0.08πt)时,P0的刚度系数关系曲线。可以看出,当P0=3 MPa的刚度曲线变化速率明显比P0=7 MPa快。图8、图9分别为V0不变,x=0.1 sin(0.08πt)时,V0的刚度系数关系曲线,当V0=1.68 L的刚度曲线变化速率明显比V0=4.2 L的快。从以下两个方面可以得出。
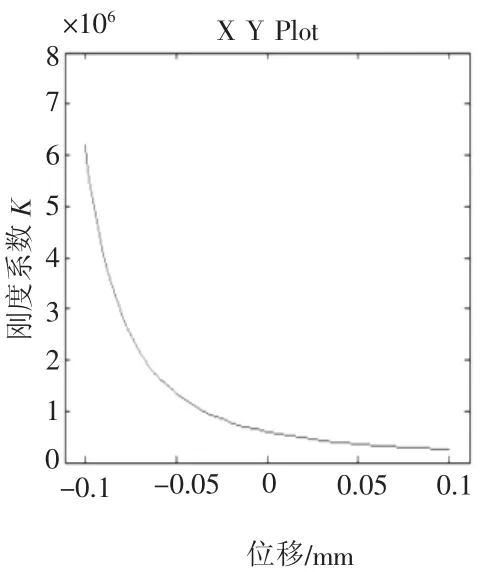
图6 V0不变,x=0.1 sin(0.08πt)时,P0=3 MPa的刚度系数关系曲线
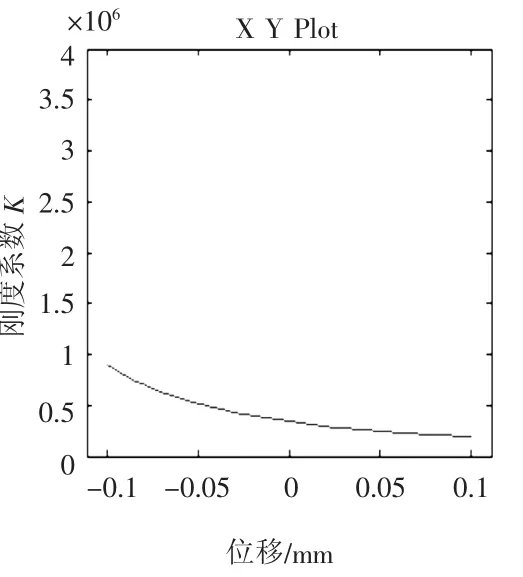
图7 V0不变,x=0.1 sin(0.08πt)时,P0=7 MPa的刚度系数关系曲线
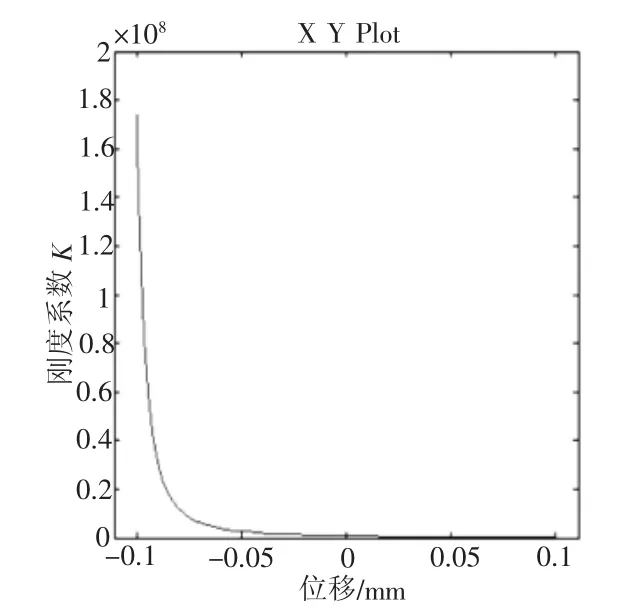
图8 P0不变,x=0.1 sin(0.08πt)时,V0=1.68 L的刚度系数关系曲线
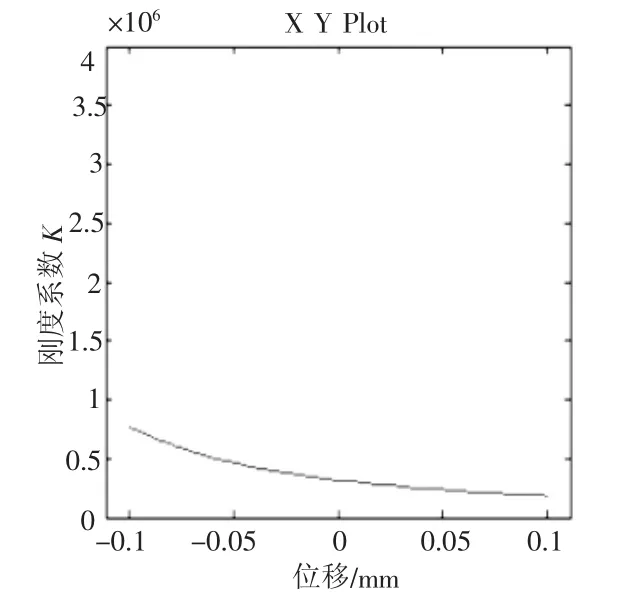
图9 P0不变,x=0.1 sin(0.08πt)时,V0=4.2 L的刚度系数关系曲线
(1)在相同的悬挂位移下,蓄能器的大小不影响悬挂刚度,与蓄能器初始充气的体积有关。因此在选择蓄能器大小时,应根据车桥载荷分布情况,确定好初始体积的大小。
(2)在相同的初始气体体积情况下,当选择好蓄能器大小,即确定初始气体体积,可以通过改变气体初始的压力来改变悬挂的刚度[4-5]。采用不同的初始压力可以满足不同路面(不同位移情况)的刚度要求,提高工程机械行驶的平顺性。
3.2 试验验证
针对仿真试验给出的试验参数,在油气悬挂试验台上进行试验验证。悬挂油缸通过试验台伺服油缸给激励位移信号,并采集其力的数据。
从试验数据曲线可以得出,当位移信号x=0.05 sin(0.08πt)时,力与位移的关系试验曲线如图10所示,试验曲线与仿真数据图2基本一致;当位移x=0.1 sin(0.08πt)时,力与位移的关系试验曲线如图11所示,试验数据与仿真曲线图6基本一致。
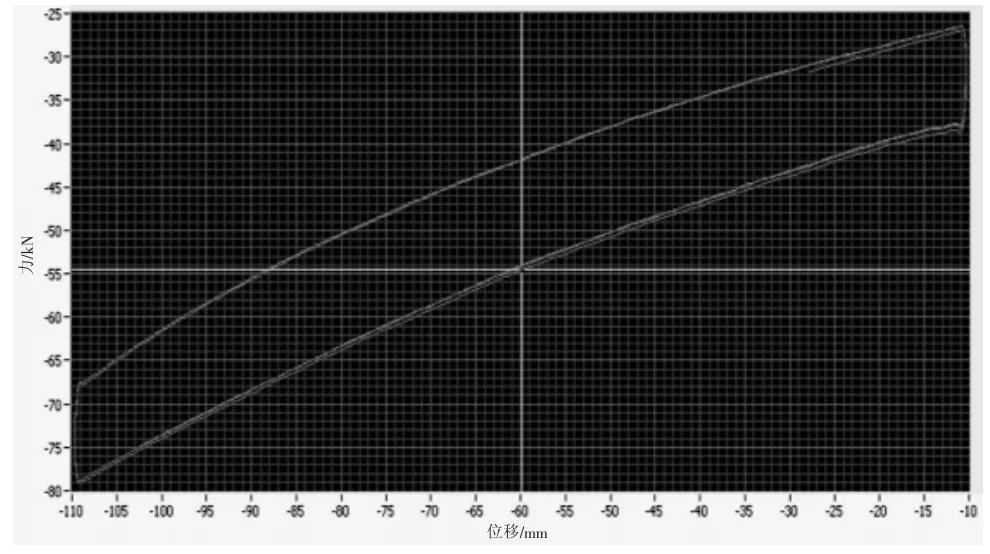
图10 力与位移的关系试验曲线(位移幅度0.05 m)

图11 力与位移的关系试验曲线(位移幅度0.1 m)
4 结语
通过仿真与试验验证,得出以下结论。
(1)油气悬挂数学模型进行仿真的数据与试验结果基本一致,即力的大小和位移的大小基本一致。验证了数学模型的正确性。
(2)影响油气悬挂刚度特性因素有:初始气体体积与压力、输入位移信号、悬挂油缸有杆腔与无杆腔的截面积。初始气体的压力易于改变,因此可以设置不同的初始压力值以满足不同路面(不同位移)的刚度要求,提高工程机械设备行驶的平顺性。
(3)数学模型没有考虑液压油的压缩性、压力损失,以及温度对悬挂系统的影响等因素,因此仿真存在比较小的误差,但整体上仿真模型的计算结果和试验结果基本一致,具有实际的参考价值,为油气悬挂系统油缸刚度参数匹配、平顺性优化设计提供了理论依据。

