基于模糊预测技术的永磁同步潜水电机控制研究

殷海双，朱哲，徐建勇，常正胜，刘博

(1.东北石油大学 电气信息工程学院，黑龙江 大庆 163318； 2.中如建工集团有限公司, 江苏 如皋 226500；3.大庆油田有限责任公司天然气分公司，黑龙江 大庆 163457)

0 引 言

永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因其损耗与温升低、单位功率密度大、维护方便、轻载运行高效等优点，被广泛应用于工业，军事，航天等领域[1]，如专门在水下使用的潜水电机，这种电机与泵直连，构成一体，形成潜水电泵，长期潜入各种水质的污水中工作。在潜水电机的研究领域内，减少温升与损耗并优化电机结构一直是热点。文献[2]针对水下环境，对45 kW充水式潜水电机改造并研制出MS200- 45型井用潜水电机并验证了电机功率因数和效率的提高；文献[3]针对大型干式潜水电机，提出采用有限元法研究其内部温度场分布和电场的分布特性，并分析了电机定子电场对电机绕组绝缘的影响，对后续潜水电机的优化与设计方向有重要的引领作用；文献[4]通过有限元技术优化永磁同步电机，并将这一技术应用在7.5 kW的潜水泵。实验显示节能效果得到了增强。

随着现代计算机处理性能大幅度提升，各类控制算法得到开发和优化，并应用在PMSM上。文献[5]采用了永磁直驱电机对潜水泵进行调速驱动，利用遗传与粒子群算法提出了有限元多目标优化的方案，并通过实验证明了电机效率的提高与损耗的减少。文献[6]提出一种基于模糊算法的电流预测控制，有效减少了电机运行时的振荡及静态误差；文献[7]在PMSM预测控制采样期间施加了两个电压矢量并设计模糊逻辑控制器确立两者占空比，达到在参数不确定的情况下准确估计电机变量的效果；文献[8]在模型预测直接转矩控制的基础上，设计模糊控制器替代速度环中的传统PI，有效提高了电机的抗扰动能力。文献[9]针对SVPWM提出一种简化算法，将三减函数转化为四则运算，在STM32嵌入式平台通过实验进行了验证；文献[10]提出用模糊PI控制器替代传统PI，改进电动车用永磁同步电机，通过仿真实验证明了其对电动车加速的优化以及转矩振荡的减小；文献[11]针对300 rpm以下的低速PMSM，提出用电压补偿的控制策略来减小电流谐波，经仿验证谐波受到抑制且转矩脉动得到了控制。

上述研究探索了各类智能控制算法在永磁同步电机应用中的可行性，但其中大多仿真与实验条件未涉及到永磁同步电机在特殊工况下的运行特性。文中针对永磁同步潜水电机，根据现有预测控制算法的不足提出一种对预测误差实时补偿的模糊预测技术，先在速度环建立预测控制系统替代传统PI，再利用模糊控制对预测控制中的转速误差量进行实时校正，形成模糊预测控制。这种算法结合的优势在于：将模糊控制引入预测控制，可通过前者强大的自适应功能有效弥补后者处理非线性系统的不足，成为一种高精度、适应性广、鲁棒性强的控制手段。经仿真测试验证，永磁同步电机能在变频起动与恒压供水两个工况下稳定运行并展现出优秀的动静态特性与抗扰动能力。

1 潜水电机工况分析及数学模型

1.1 潜水电机的负载起动

若令电机直接起动，前端没有阻力水流，会导致水泵系统内流量短时间内突变，压强大幅度波动，对管道产生冲击使管壁受力出现噪声，这种现象被称为“水锤”效应。解决水锤效应需在电机起动时遵循以下原理：常规状态下电机转速与泵转速相等，泵系统的流量Q与转速N之间关系式如下：

(1)

而转速N与液流压力P关系如下：

(2)

由式(2)可知，泵输出流量变化与电机转速成正比，压力与速度的平方成正比。

电机的转矩T与转速N之间关系如下：

(3)

即：

(4)

可明显看出，在电机起动中，让转矩与转速依照式(4)的特定关系变化，可以有效降低转矩的突变，减少流体对管道与叶轮的冲击，避免发生“水锤”现象。

1.2 恒压供水的原理及模型

恒压供水的系统流程图如图1所示，图中水泵机组由控制柜，变频器，电机，水泵组成。出口水压的控制采用PID技术，输入为设定水压，输出为实际采样水压的测量值，T(s)为扰动，在文中代表用户用水流量。

恒压供水的数学模型可用式(5)表示：

(5)

式中T1代表惯性时间常数；k1为系统的增益值；τ为时滞常数。

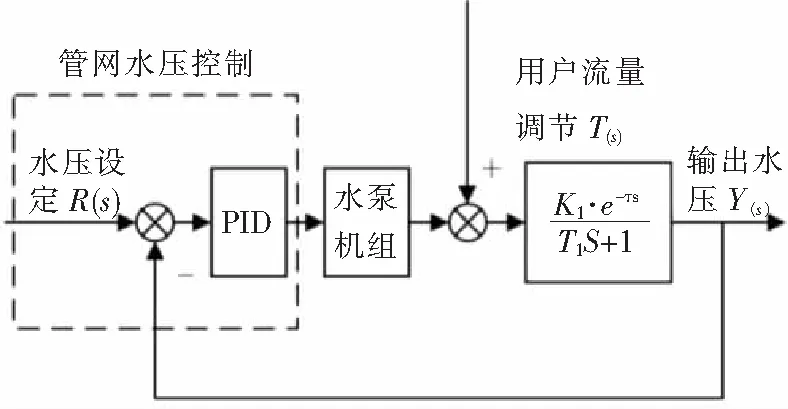
图1 变频控制恒压供水系统流程图

考虑到供水系统中其他装置例如电控制柜、变频器调节、压力检测等滞后时间，本文将其等效为比例关系，如式(6)所示：

G3(s)=k3

(6)

式中k3为压力检测的增益。

供水模型时间参数的选取参考了文献[12]，该文献将电机程序简化为变频器的传递函数以处理2 000 s时长的供水仿真。但文中还原了完整的电机控制系统，CPU负荷过高。因此经过调试，按100:0.05的比例压缩仿真时长与延时参数，在仿真合理运行的同时保证了供水过程的完整。设计的供水模型传递函数如式(7)所示，仿真时长为4 s：

(7)

2 模糊预测控制设计

2.1 模糊预测控制的原理与结合方式

模糊预测技术，即模糊控制与预测控制算法的结合。本文所采取的结合思想是利用模糊技术对预测误差做补偿。在永磁同步潜水电机的控制设计中，电流环保留了传统的电流预测系统，速度环首先根据MPC算法的原理建立转速预测控制器，由于在控制的反馈校正过程中，转速跟踪误差的抑制参数对电机系统影响较大，因此在转速预测控制的基础上建立模糊控制器，动态校正这一参数，使其能够随着转差的变化而对系统做出实时的调整。

2.2 速度环转速预测控制设计

在电机转速环上建立转速预测控制系统代替传统PI，过程如下：

由于文中是建立在id=0的矢量控制基础上研究的，因此电磁转矩公式可转化为Te=1.5Pnψfiq，永磁同步电机转速与转矩关系式如下：

(8)

式中Te为电磁转矩；Tl为负载转矩；ωr为转速。求解系统的连续频域方程，将式(8)等号两边分别拉普拉斯变换，得到频域公式如下：

(9)

将式(9)根据Z域离散化求解可得到传递函数如下：

(10)

再将其转化为差分方程如下：

ωr(k)=a0iq(k-1)-b0ωr(k-1)

(11)

ωr(k+1)=a0iq(k)-b0ωr(k)

(12)

式中T为采样周期；Km=1.5Pnψf；a0=Km(1-e-TB/J)/B；b0=-e-TB/J。ωr为第kT时刻的实时转速。

由上述两差分方程相减可得到理想状态下，永磁同步电机速度环的预测控制方程如下：

(13)

由式(13)加上系统运行过程kT时刻的误差量e(k)，即可得到系统的预测输出量：

ωrp(k+1)=ωrm(k+1)+e(k)

(14)

预测控制系统要根据预测输出与目标函数，将实际运行状态向期望的模型平稳的校正，这个过渡过程即参考轨迹，方程如下：

yr(k+1)=αωr(k)+(1-α)ωref(k)

(15)

式中α是柔化系数；ωref(k)是系统的初始量。

根据模型预测控制算法中的反馈校正原理，式(14)与式(15)为系统预测输出的过程设计二次优化，目的是使预测输出量更加贴近目标函数，同时尽力使过渡过程平滑避免状态突变，对水锤效应起到一定的规避作用。

性能指标方程如下：

(16)

式中Ec是抑制跟踪误差的增益；β是抑制控制量变化的增益。

(17)

因此，在kT时刻q轴电流给定值如式(18)：

(18)

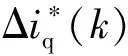
转速预测控制整体的闭环结构如图2所示，其中反馈校正建立在参考轨迹逼近目标函数的过程中，可使转速、转矩等参数的预测量和目标函数得到二次优化。

图2 转速预测控制结构框图

2.3 速度环模糊预测控制设计

在反馈校正系统中，抑制跟踪误差的输入权值(Er)在运行中保持初始量不变，导致调参困难并影响控制的精确度：Er数值过大会使电机动态响应速度剧增，但易发生超调；Er过小会令转速过渡平稳，但同时会存在静态误差，产生振荡。

以本文建立的转速预测控制系统为基础，通过构建模糊控制器来优化转速预测中用于抑制跟踪误差的权值Er，输入Er与实际转差n′，将Er转化为动态参数以调整电机当前速度。

模糊控制器的原理与构建流程如图3所示，在二维模糊控制中，系统输入量x经过增益Ke转变为模糊控制器的输入误差e；ec为误差的变化率，由输入量x经过微分模块和增益Kec获得；u*为真实值输出，由模糊控制器输出u乘以输出增益Ko获得。

图3 模糊控制流程框图

Ke、Kec和Ko的计算如下：

(19)

Kec=ke/Δt

(20)

(21)

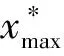
考虑到仿真对象是额定转速为3 000 r/min的潜水电机，所以转速误差的实际范围在[-3 000,3 000] r/min，设定该误差的论域在[-600,600] r/min之间。这代表当转速误差超过600 r/min时，模糊控制的隶属度函数始终输出最大值；误差在[-600,600] r/min范围内时，根据隶属度函数、推理机构和去模糊化确定最终输出校正值。为了方便计算，基础论域的取值适合在1左右，文中定为[-1.2,1.2]，根据式(19)计算，Ke=0.002。

为方便计算，e与ec的论域通常相同，离散系统的采样时间Δt根据经验估测为0.002 s，根据式(20)计算求得kec=1×10-6。

实际输出信号u*的范围±600之间，输出论域u在±1.2之间，根据式(21)计算Ko(即u的比例因子)为500。需注意，论域和比例因子根据调试经验确定，合理的参数设定并不唯一。

模糊控制技术的结构框图如图4所示。

图4 模糊预测控制结构图

实际转差n′经模糊化处理，推理机构以及去模糊化后形成动态的模糊校正系数η，普通转速预测控制的权重系数Er经过模糊校正后得到式(22)：

Er′=Er(1+η)

(22)

(1)参数模糊化

根据上文提到的参数选取得出控制参数模糊化图表如表1所示。

表1 参数模糊化

论域中7个值从小到大对应的语言值分别为负大(NB，Negative Big)，负中(NM，Negative Middle)，负小(NS，Negative Small)，零(ZO，Zero)，正小(PS，Positive Small)，正中(PM，Positive Middle)，正大(PB，Positive Big)。

(2)设计语言值的隶属度函数

文中根据系统的论域采用了离散量化的隶属度函数，函数类型为高斯(Gaussmf)，变量e与ec的隶属度函数如图5、图6所示。

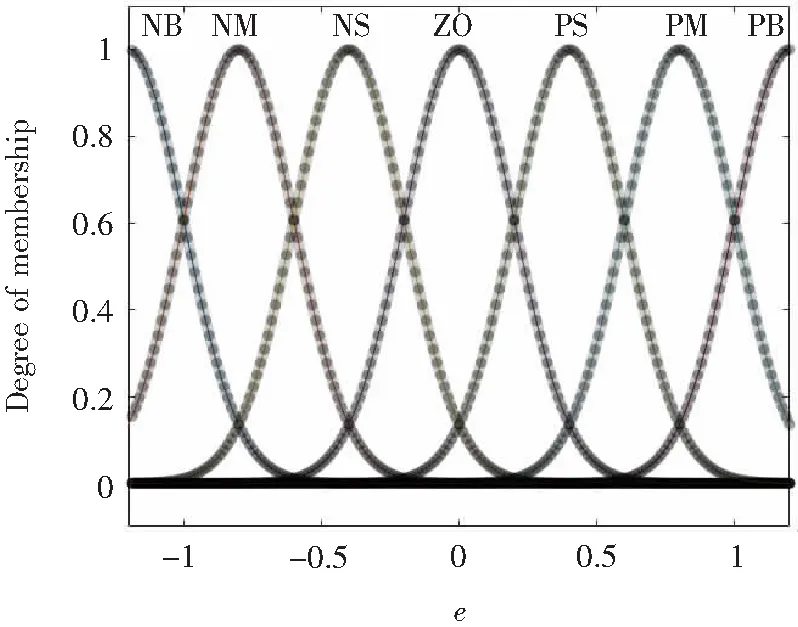
图5 变量e的隶属度函数

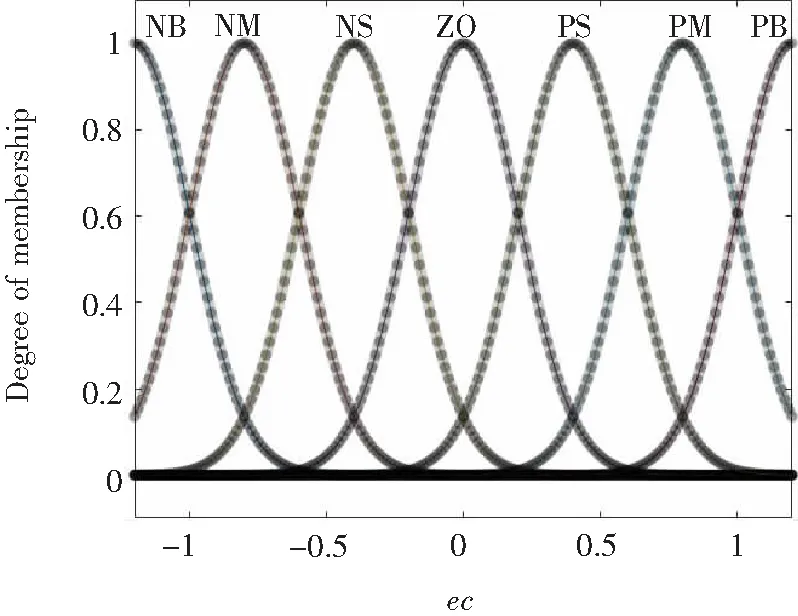
图6 变量ec的隶属度函数

输入电机转差在经过比例因子Ke、微分模块及比例因子Kec后，变换到[-1.2,1.2]的范围内。e与ec的隶属度函数均为高斯函数，均匀分布在[-1.2,1.2]范围内，对称轴分别为-1.2, -0.8, -0.4, 0, 0.4, 0.8, 1.2。

(3)建立模糊控制规则

建立如表2所示的模糊控制规则表，当电机转差、转差速率较大时，增大转速预测控制的权重系数Er，即模糊校正系数η应取较大的值，以获得更大的转速响应速度，尽快降低转差达到给定值；当电机转差、转差速率较低时，入股模型预测控制的权重系数过大导致电机转速超调，此时为了达到最佳控制效果，适当减小权重系数Er，即模糊校正系数η应取较小的值，以减少电机转速超调量，使电机的转速更平稳的过渡到稳定值附近。

表2 模糊控制查询表

(4)e与ec隶属度输出曲面

根据上述模糊隶属度函数、模糊规则表，建立模糊控制器，系统输出如图7所示的模糊输出曲面，代表e与ec隶属度函数输出的分布。该曲面输出值在[0,1]之间，根据当前系统反馈的转速差和转差率，通过查询的方式确定不同e/ec组合对应的模糊校正系数η，对转速预测控制的权重系数Er进行校正。由图7可知，当e/ec的绝对值较大时，输出值u随之增大并接近1，这表示根据专家经验，当转速差、转差率比较大时，权重系数Er增加以获得更快的响应速度；当e/ec的绝对值比较小时，输出值u也比较小，接近0，这表示根据专家经验，当转速差、转差率比较小时，权重系数Er的增量减小以降低静态误差，控制振荡。

基于模糊预测的电机控制结构如图8所示。

图7 模糊输出曲面(e与ec)

图8 基于模糊预测的电机控制结构

3 系统仿真与测试

为验证模糊预测控制对潜水PMSM的优化效果，在Matlab/Simulink搭建仿真模型，结合实际的工程案例模拟负载起动与恒压供水两个工况，同时将本文所设计的控制策略与双闭环矢量控制、预测控制两种算法的控制效果进行对比。

在预测控制参考轨迹中，柔化系数α影响本周期与上一周期预测值的权重。α越接近于1，代表本周期预测值的比重越大。根据经验，为了让预测输出更加平滑，α应在0.9～1之间取值，文中取为0.995。权值β用于抑制控制量变化，β的选取参考了文献[13]的设计，取值为1。

3.1 负载起动测试

仿真参考的实际工程案例选择某自来水公司15号井数据。15号井选用的电机型号为UT(G)200-30，其参数与该水厂某日的运行案例如表3所示。

表3 UT(G)200-30永磁同步潜水电机参数

仿真条件如下：仿真时长0.25 s，同步转速由表4推算出为2 400 r/min。

表4 某自来水公司15号井运行数据

转矩与转速关系按照文中1.1的结论设定，即：

(23)

具体比例为：

(24)

式中T为转矩；N为转速；Te为额定转矩95.5N.m；Ne为同步转速2 400 r/min。T和N在达到运行数值的过程中按照式(12)的比例关系动态变化。

运行结果如图9所示，观察三种算法控制的电机转速波形：使用文中的模糊预测控制，电机转速峰值为2 456 r/min，超调量仅有0.233%；而基于预测控制的转速超调为0.643%；传统矢量控制超调量为1.138%。同时基于模糊预测控制的电机在运行0.077 s时就达到稳定状态；预测控制的电机需要0.107 3 s；而矢量控制的电机需0.137s。可以看出。在潜水电机起动的工况下，基于模糊预测的控制策略超调量更小，更快达到稳定状态。

图9 负载起动转速波形对比

接下来观测运行过程中的转速误差变化曲线。

如图10所示，模糊预测技术对于转速误差的控制效果良好，相比于另外两种算法，曲线变化更加平滑；同时可以发现与2.3节的设定相符，当误差超过600 r/min时系统以最大的控制量进行调整，过程迅速。当误差低于600 r/min时根据模糊控制的输出进行实时校正，过程较为平滑。而另外两种算法由于没有自适应调整，导致转速曲线有突变现象，难以适应潜水电机的工况。

图10 转速误差曲线

最后观察三种算法的q轴电流对比。

q轴电流变化对比如图11所示，基于本文模糊预测的电机系统，q轴电流超调量为45.60%；基于预测控制的iq超调量为55.96%；矢量控制超调量110.7%。相比之下本文的控制策略q轴电流超调量最小，可有效提高电机起动的稳定性与安全性。

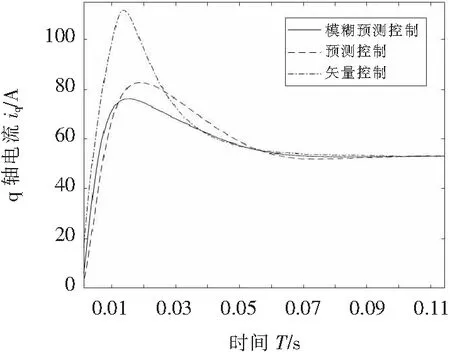
图11 q轴电流曲线对比

3.2 恒压供水测试

根据某水厂提供的真实供水案例：当日，该水厂通过一台电泵向某区用户恒压供水，出口水压设定为0.43 Mpa。早上8:00，客户用水量为4 768 m3/h，上午11:00，用水量达到4 959 m3/h。根据1.2节中推出的供水模型，带入设计的电机控制系统模拟恒压供水。Matlab/Simulink仿真结构图如图12所示。

其中转速给定系统如图13所示。

仿真条件设置如下：除转速外，其余电机参数与上一节仿真设定相同(转速变成了一个随水压与流量变化的变量)，仿真时间为4 s，出口压力设定为0.43 MPa，初始的居民用水流量为4 768 m3/h，在第2 s开始阶跃上升至4 959 m3/h。运行仿真，观察三种电机控制算法对水压的调控效果。

图12 Matlab仿真结构框图

图13 转速给定系统结构

由图14可看出，应用模糊预测技术的潜水电机对恒压供水系统有较为明显的改善。就超调而言，模糊预测控制的水压超调量为23.70%，预测控制为27.23%，矢量控制为36.56%；同时，相比于模糊预测技术，预测控制存在着大量的静态振荡，这也验证了模糊控制对权值Er的实时整定会给系统带来可观的优化。

图14 恒压供水水压波形对比

4 结束语

文章针对矢量控制、预测控制技术在永磁同步潜水电机应用中的不足，结合恒压供水的工况设计了模糊预测控制算法，通过对两个工程案例的仿真验证了这种算法的改善：基于模糊预测控制的永磁同步潜水电机，负载起动时转速变化更平稳，超调小，动态响应快，q轴电流更稳定；将应用文中控制策略的电机带入恒压供水系统，会使水压变化幅度减小，同时消除了静态振荡。