基于分数阶黏弹性模型的混凝土阻尼频率相关性研究

梅生启, 李韶华, 李鹏飞, 徐浩然, 张元昊

(1.省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄 050043；2.石家庄铁道大学 土木工程学院，石家庄 050043；3.桥梁结构安全技术国家工程实验室，北京 100088)

阻尼作为反映系统耗能特征的重要参数之一，对控制系统在稳态及随机激励下的振动响应幅值，保证动力系统稳定性有重要作用[1]。实际结构分析时，阻尼取值的不同，会造成分析结果间明显的差异[2]。2020年5月，我国悬索桥虎门大桥桥面发生明显振动，经专家组判断由于阻尼原因导致桥梁振动的平息时间较长[3]。目前我国[4-5]、欧洲[6]及美国[7]等国家和地区的规范中，建议一般情况下混凝土结构阻尼比取值为5%。但Newmark等[8]对大量的试验测试数据分析后发现结构在不同外部作用下的阻尼值并不相同。由于结构形式的多样性和内外影响因素的复杂性，导致结构阻尼发生改变，其准确取值仍是一个难题。

刘铁军等[9-10]通过试验研究发现，在混凝土结构弹性阶段及破坏前期，混凝土材料阻尼是结构阻尼的主要来源。Chung[11]认为材料的阻尼性能不仅依赖于材料自身，还依赖于外部荷载频率，正如黏弹性响应依赖于荷载频率一样。Kimball等[12]对多达18种固体材料(包括木材、金属等)进行测试发现，弹性范围内这些固体材料的内耗并不服从黏滞定律，而与应变幅值相关。基于经典黏滞理论计算的体系每周振动能量损失依赖于激励(或反应)频率，被认为与试验结果不符[13]。Chopra[14]在金属结构的试验中发现循环变形过程中内部耗散能量基本上与循环频率无关。但对于混凝土材料，Zhang等[15]对聚合物改性水泥浆体的阻尼性能进行测试发现，其阻尼性能不仅与温度相关，还与频率相关。梁超锋等[16]通过试验发现，在0.5～1.0 Hz内，不同类型纤维混凝土的损耗因子随频率降低较快，在1.0～2.0 Hz内渐趋平缓，基于经典整数阶黏弹性模型可以分析单一频率时的损耗因子。Mei等[17]通过对C50普通混凝土进行轴压滞回测试发现，损耗因子随滞回频率提高呈非线性降低趋势，但采用经典整数阶黏弹性模型只能对单一频率滞回曲线进行分析，无法反映整体的耗能频率相关性。

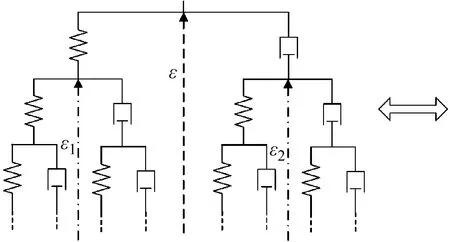
如果将经典黏弹性模型中的弹性元件应力应变关系表示为：σ(t)=Ed0ε(t)/dt0，黏性元件的应力应变关系表示为：σ(t)=μd1ε(t)/dt1。那么介于纯弹性体和纯黏性体之间的黏弹性材料的应力应变关系可采用一种分数阶微积分σ(t)～dαε(t)/dtα(0≤α≤1)进行表征。由于在整数阶经典黏弹性模型中, 单个黏性元件只描述单一滞后机理，Schiessel等[18]通过频域内的运算证明, 分数阶黏性元件的力学模型可看成是由一系列弹簧和黏性元件组成的树状分形网络模型，如图1所示，可以更好反映整个受力范围内的材料黏弹性。Bagley等[19]采用三参数分数阶模型拟合了黏弹性材料特性，发现分数阶模型能够在非常宽的频率范围内与试验数据吻合良好。Jia等[20]采用分数阶模型进行阻尼器滞回性能的研究分析。

为进一步分析外部荷载频率对混凝土材料阻尼的影响，本文分别采用经典黏弹性模型和修正分数阶黏弹性进行计算分析。首先采用整数阶Kelvin模型对普通混凝土和再生混凝土的阻尼频率相关性进行分析。结合测试数据规律提出分数阶Kelvin模型和修正分数阶模型，校准分数阶黏弹性模型的描述效果。然后收集了国内外152组测试数据，分析了不同条件下的混凝土阻尼频率相关性规律，并分别采用经典黏弹性模型和分数阶模型进行计算分析，验证分数阶模型对混凝土材料动态耗能性能的计算分析效果。

(a)

1 基于整数阶黏弹性模型的混凝土耗能频率相关性分析

作者于2017年开展了一批C50混凝土轴压滞回试验。试件尺寸为100 mm×100 mm×300 mm棱柱体，滞回荷载加载频率分别为0.2 Hz,0.5 Hz,1 Hz,2 Hz,3 Hz。具体加载工况如表1所示，其中平均力为滞回过程中的平均荷载，加载幅值为滞回过程达到的最大荷载。

表1 C50混凝土试块加载工况

基于滞回试验测试结果，可以对表征混凝土阻尼性能的损耗因子进行计算。基于试验滞回环曲线计算损耗因子与频率的关系如图2所示。

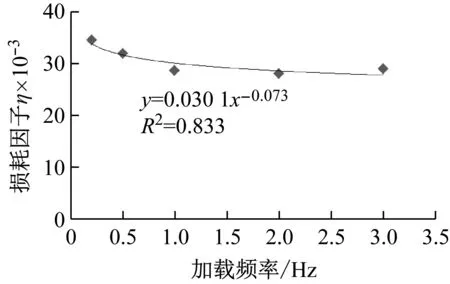
图2 滞回加载频率与损耗因子的关系

从图2中可以看出，随着频率的增加，混凝土阻尼呈非线性降低。导致这一现象的原因可能是由于混凝土中骨架体系随荷载近似弹性变形实时，而黏性变形为材料黏弹性导致的滞后变形，如反映在时间维度上即应力应变曲线存在相位差。为进一步计算混凝土的耗能频率相关性，采用黏弹性模型进行分析。梁超峰等、欧进萍等[21]、苏力[22]先后采用经典整数阶Kelvin模型进行计算分析，发现可以良好模拟混凝土在单一荷载条件下的轴压滞回曲线。

经典整数阶Kelvin模型由弹性元件和黏性元件并联组成，如图3所示。

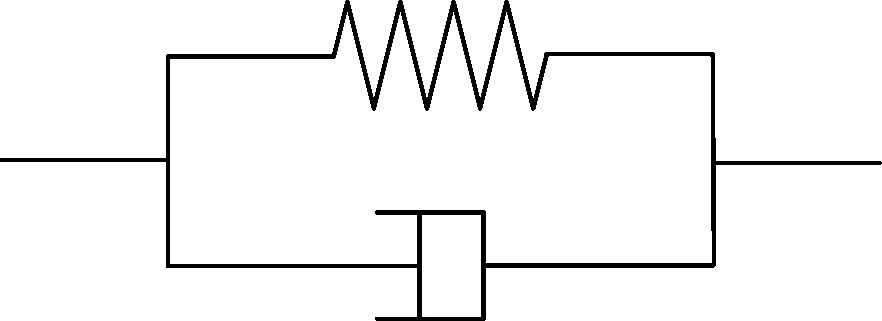
图3 经典整数阶Kelvin模型

该模型的应力应变关系可写为

(1)

式中:涉及到的材料参数有弹性模量E和材料的黏滞系数μ两项;σ(t)为应力;ε(t)为应变。

对式(1)进行Fourier变换，可得到

σ(ω)=(E+μωi)ε(ω)=(E′+iE″)ε(ω)

(2)

式中:E′=E为存储模量；E″=μω为耗散模量。

由式(2)，可得经典整数阶Kelvin模型的损耗因子频率相关性表达式为

(3)

目前的经典整数阶黏弹性模型主要是基于单一荷载工况下的每周滞回耗能面积和损耗因子进行模型参数识别，利用经典整数阶模型进行了混凝土耗能频率相关分析尚较少见到。

2 基于分数阶微积分的黏弹性模型修正

何明明等[23]、赵永玲等[24]、朱俊涛等[25]先后采用分数阶黏弹性模型对岩石、沥青等材料的动态黏弹性行为进行分析，发现采用分数阶黏弹性模型可以实现更少的参数来反映不同材料在动态荷载下的耗能行为。

如将弹性元件的应力应变关系表示为

(4)

黏性元件的应力应变关系表示为

(5)

那么介于纯弹性体和纯黏性体之间的黏弹性材料的应力应变关系可采用一种分数阶微积分进行表征,

(6)

分数阶导数的具体表达式如式(7)所示。

(7)

将经典整数阶Kelvin模型中的黏性元件替换为分数阶元件，即可形成分数阶Kelvin模型，如图4所示。

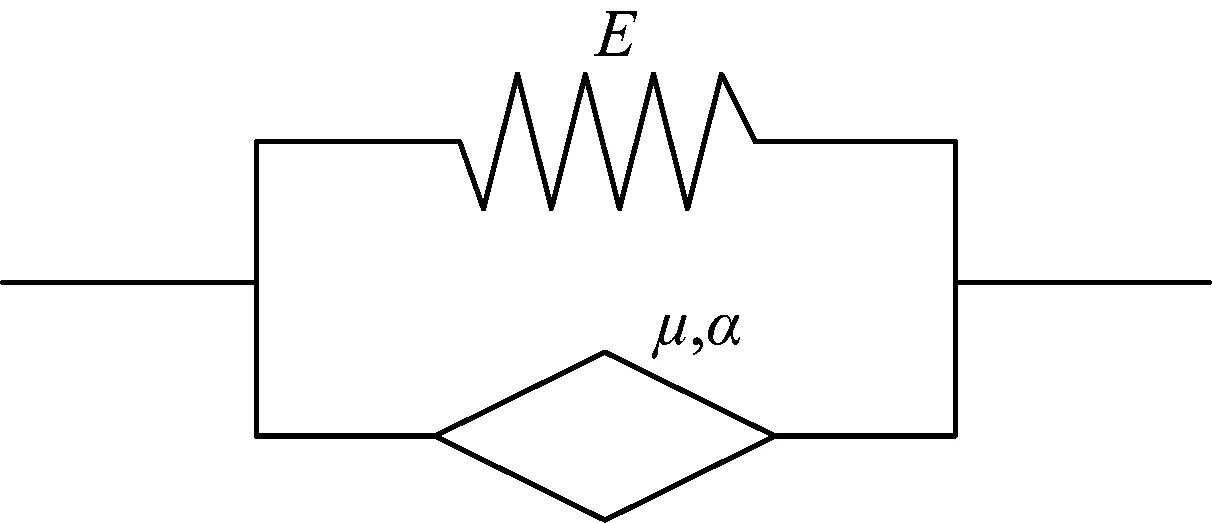
图4 分数阶Kelvin模型示意图

则分数阶Kelvin模型的应力应变关系为

σ(t)=Eε(t)+μDαε(t)

(8)

式中，a为分数阶导数的阶数，当a=0时模型退化为纯弹性元件，当a=1时模型退化为经典Kelvin模型。

对分数阶Kelvin模型进行Fourier变换，并引入iα=cos(απ/2)+i·sin(απ/2)，得到分数阶Kelvin模型损耗因子为

(9)

由式(9)可知，由分数阶Kelvin模型计算出的损耗因子与频率和导数阶数呈非线性正相关。以E=3.42×104MPa，μ=117 MPa·s为例进行分析。保持E和μ不变，改变分数阶导数，得到的损耗因子结果如图5所示。

图5 分数阶Kelvin模型的损耗因子参数分析

可以看出，当a趋近于1时，分数阶模型逐渐退化为经典整数阶模型。可以通过导数阶数的改变，更好模拟不同黏弹性的材料动态性能。但由于分数阶Kelvin模型计算的耗能与频率呈非线性正相关性，与测试数据规律不完全相符，因此还需寻找一类耗能频率非正相关模型进行计算分析。

根据测试结果，无论是正弦波还是方波轴向滞回加载，得到的损耗因子随着滞回频率的提高呈非线性降低趋势。而Kelvin模型中的弹性元件与黏性元件并联，意味着弹性和黏性变形的大小相同。而研究人员通过纳米压痕等微观试验观察发现，混凝土黏弹性能主要是由于内部水和凝胶体组成的。在滞回变形过程中，骨料及硬化浆体形成的混凝土骨架体系近似弹性变形，而水和凝胶体等会出现滞后黏性变形。考虑分数阶黏性元件的导数阶数可变性，提出修正分数阶黏弹性模型为两个分数阶黏性元件并联，分别用来表示滞回过程中的弹性变形和黏性变形。模型示意图如下所示，其中两个黏性元件根据不同加卸载阶段可以分别变化为弹性元件、整数阶黏性元件和分数阶黏性元件。

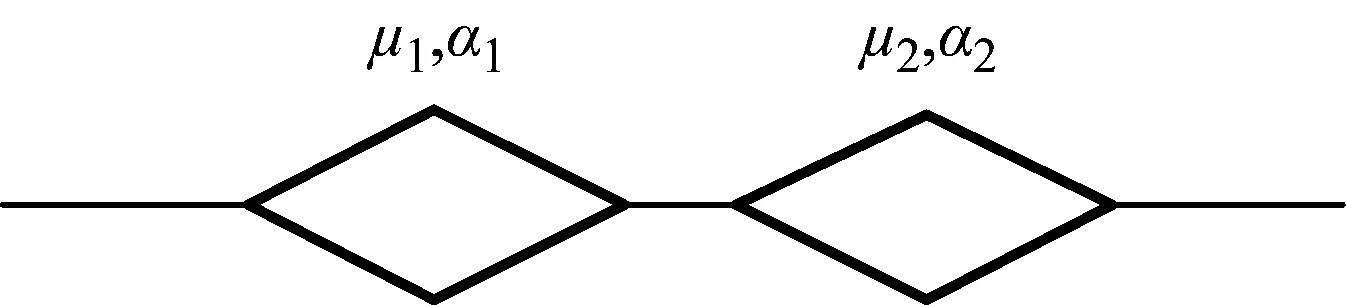
图6 修正分数阶模型示意图

对应模型应力应变关系为

(10)

式中,a1μ1，a2μ2分别为对应材料参数。

因为混凝土黏弹性在弹性阶段的表现更为明显，因此模型可变化为弹性元件与分数阶黏性元件串联，对应应力应变关系对应为

(11)

对修正分数阶模型进行Fourier变换，可得到其存储模量、耗散模量和损耗因子的表达式分别为

存储模量

(12)

耗散模量

(13)

损耗因子

(14)

以E=3.42×104MPa，μ=117 MPa·s为例，保持E和μ不变，进行分数阶模型的耗能频率相关性分析结果，如图7所示。

图7 分数阶Maxwell模型的损耗因子频率相关性参数分析

可以发现，随着频率的增加，该分数阶模型的损耗因子呈非线性减小趋势，且随着导数阶数的减小，其减小幅度也逐渐趋于平缓。通过改变导数阶数，采用分数阶导数形式的黏弹性模型可以更好模拟混凝土等材料黏弹性材料耗能随频率的增大而减小的行为。

基于本文提出的黏弹性模型损耗因子-频率相关性公式，分别采用Kelvin模型、分数阶Kelvin模型和分数阶修正模型对单一混凝土的耗能频率相关性试验结果进行计算。考虑到参数拟合的方便性，在计算表达式中引入参数τ=μ/E。得到的结果如图8所示，各模型的参数见表2。

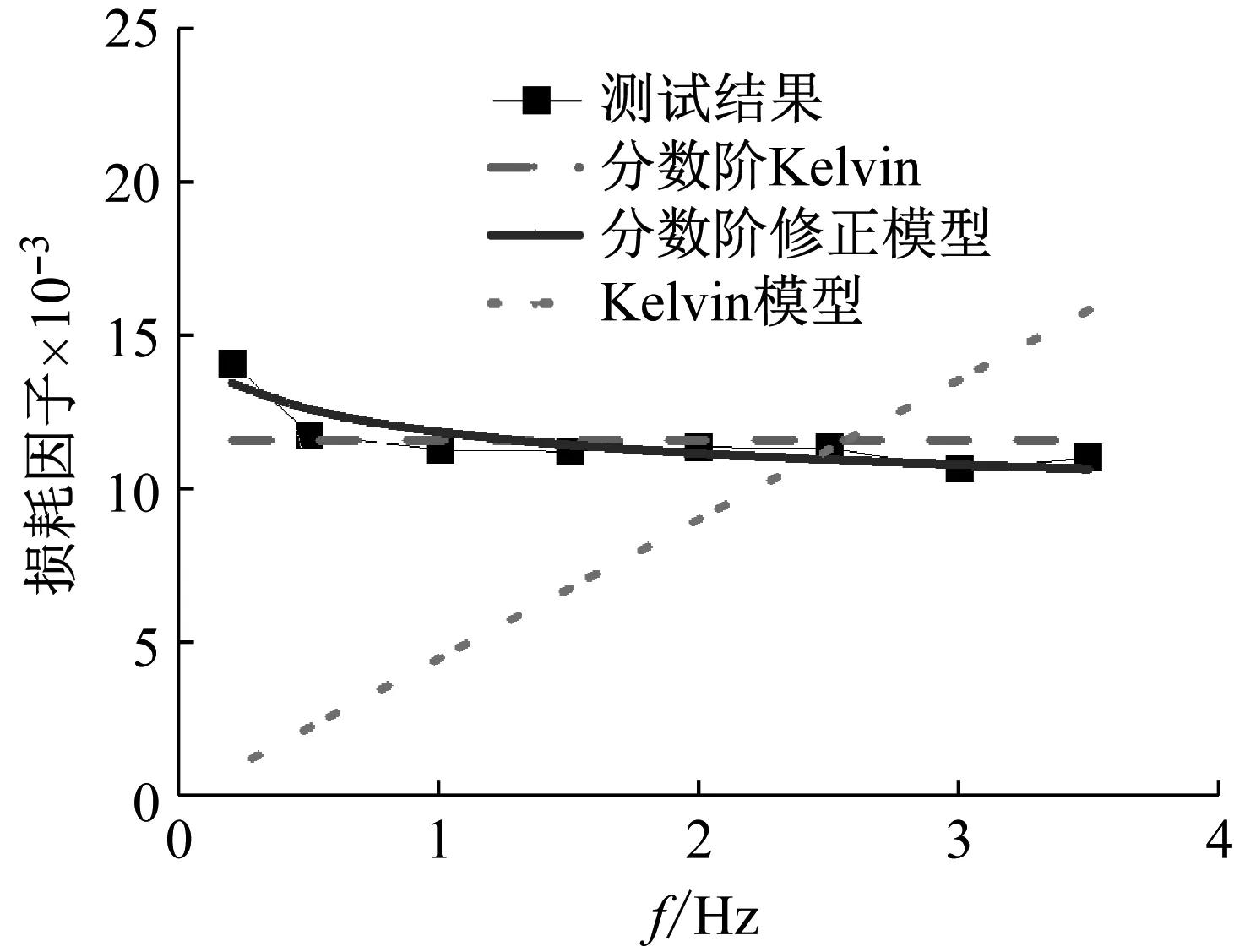
图8 黏弹性模型的混凝土耗能-频率相关性拟合结果

表2 黏性模型拟合参数

由图8可以看出，分数阶模型的计算分析效果明显优于经典黏弹性模型，尤其是分数阶修正模型的预测效果最好，最大误差仅为6%。上述结果表明，分数阶黏弹性能够良好分析混凝土材料的整体耗能-频率相关性规律，为分数阶黏弹性模型在混凝土动态黏弹性能描述中的应用提供了数据支持。

3 基于分数阶黏弹性模型的耗能频率相关性多样本数据分析

3.1 文献数据统计

为更好分析荷载频率对混凝土耗能的影响，本文进一步收集了国内外文献中采用强迫振动方法测试混凝土材料阻尼的152组阻尼测试数据进行分析。试验基本信息如表3所示，得到的测试结果如图9所示。

从图9中可以清晰看出，在0～3 Hz滞回荷载频率内，不同文献耗能能力均随着频率的增大呈现非线性降低趋势。而不同文献中的耗能能力测试结果存在一定差别，其原因可能是不同试验的荷载幅值存在差异，导致相同频率下的测试结果差异较大。同时，不同试验中所采用原材料并非完全是普通混凝土，还会有一定量掺合料对混凝土动态性能产生影响。外部荷载对混凝土材料的阻尼性能有明显的影响，但由于强迫振动测试方法的复杂性和试验设备的限制，相关的数据相对还较少。

表3 文献中的测试条件和试件信息

(a) 普通形式

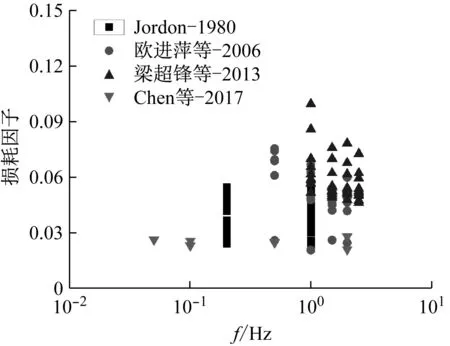
(b) 对数形式

图9中所统计混凝土材料损耗因子统计数据均小于目前建筑、桥梁等规范中规定的结构阻尼比数值，其原因可能是一方面工程结构服役期间的耗能构成中不仅包括材料阻尼，还可能包括大变形下的构件连接处摩擦阻尼、周围介质阻尼基于在地基中的辐射阻尼等[29]。目前已有研究表明结构阻尼会随着振幅的改变发生改变，如在风振下的高层建筑瞬时响应幅值的增大伴随着结构阻尼明显的改变[30]。但针对轨道交通、道路交通中快速动荷载对振动响应及阻尼的影响，目前的研究关注仍较少。目前研究表明，在弹性阶段和破坏初期，混凝土是阻尼的主要来源之一，通过材料层次的测试结果对结构的动力分析结果进行修正或分析，将会提高测试的简便性，为混凝土结构动力性能的精细化研究提供一种新的可能性。

3.2 基于统计数据的分数阶黏弹性模型验证

考虑统计数据中材料阻尼试验为弹性阶段，为进一步验证分数阶黏弹性模型计算分析的效果，分别采用Kelvin模型、分数阶Kelvin和修正分数阶模型对3.1节统计数据来计算分析。首先采用3种模型对统计数据进行统一计算，得到的结果如图10所示，各模型的参数如表4所示。

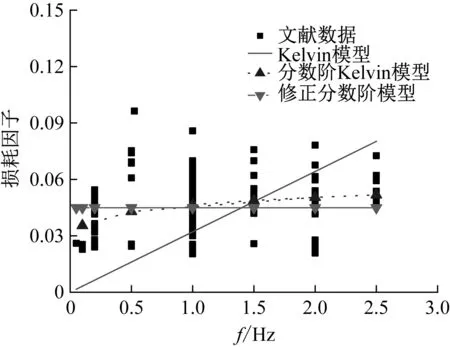
图10 基于黏弹性模型的损耗因子-频率相关性分析

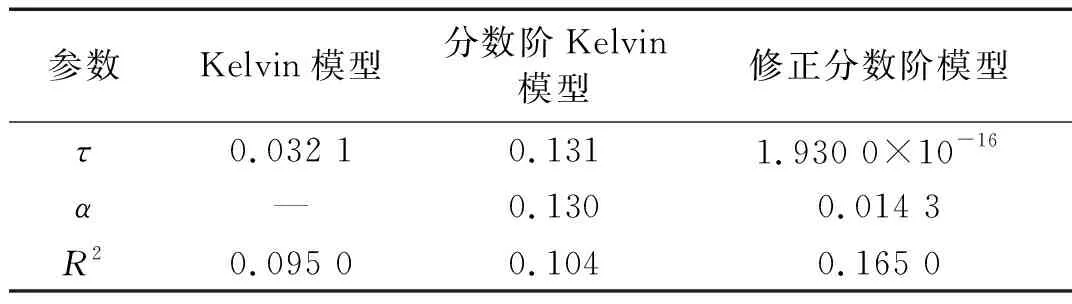
表4 基于收集数据的黏弹性模型参数确定

从图10中可以看出，分数阶模型的预测效果均较经典黏弹性模型好。由于所统计数据的离散性和条件的多样性，单一参数模型均无法对数据进行准确描述。

分别采用3种模型对文献分别进行计算分析，得到的结果如图11所示，模型参数如表5所示。

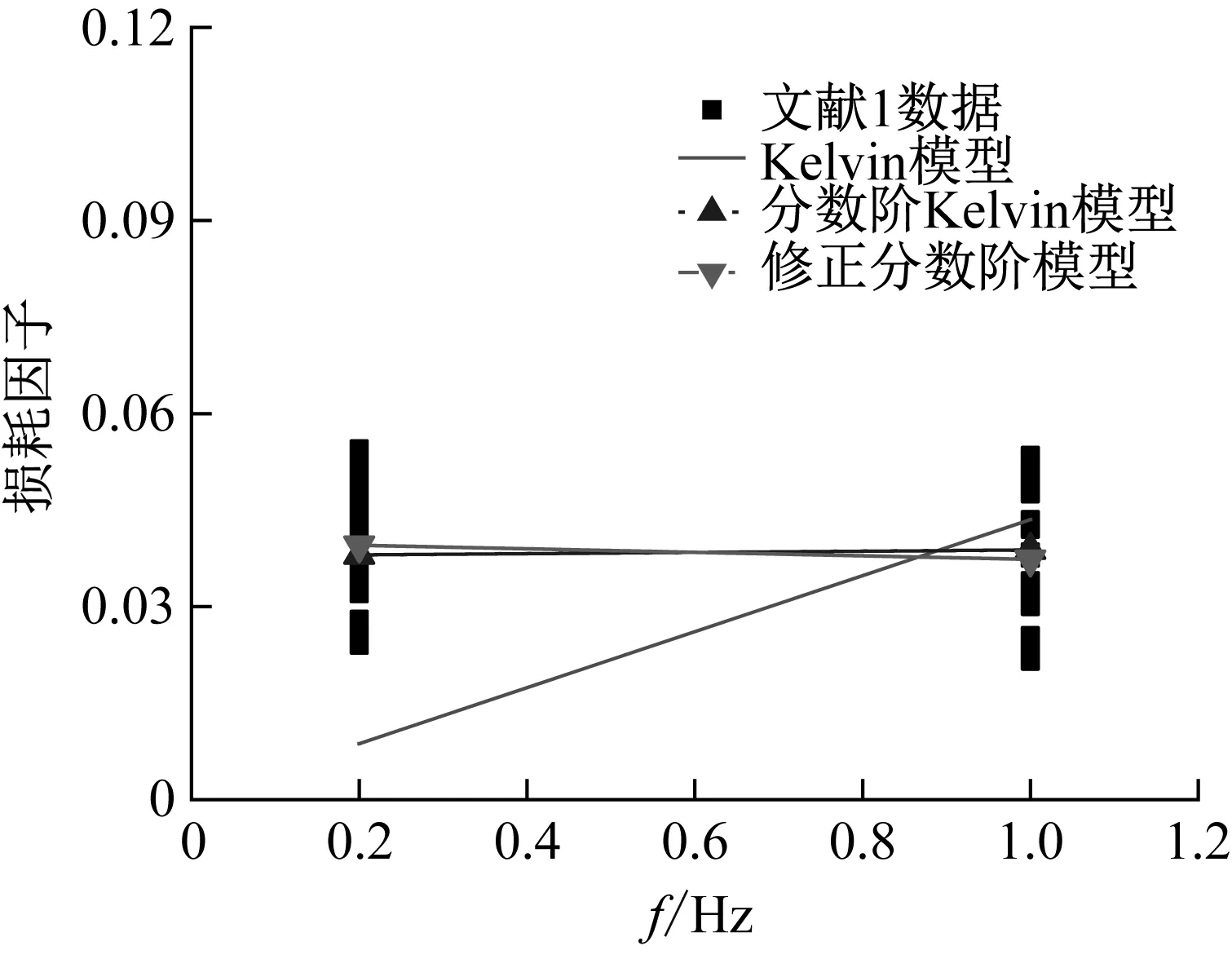
(c) 数据来源-文献3

从图11可以看出，经典整数阶Kelvin模型对混凝土阻尼-频率相关性的描述与试验现象规律不一致，分数阶微积分的引入有效改善了计算分析效果。来自不同文献数据计算结果显示，分数阶Kelvin模型的拟效果和规律与试验现象接近，尤其是修正分数阶模型，能够更好反映阻尼随频率增加的降低趋势。

为进一步分析模型计算误差分析，将计算结果与实测数据进行对比分析，如图12所示。从图12可以看出，修正分数阶模型计算结果与试验数据的误差范围主要在-50%～50%；由于Kelvin计算出的耗能随频率增加而增大，在频率较大时明显高估了材料的耗能性能，最大误差超过150%。

4 结 论

本文基于试验结果和国内外相关文献数据，从耗能频率相关性角度分析了经典黏弹性模型和分数阶黏弹性模型在混凝土材料动态黏弹性能计算分析的适用性。结果表明，采用分数阶黏弹性模型进行混凝土材料的动态分析的效果更好。

在耗能-频率相关性方面，与收集的152组试验数据对比分析结果表明，分数阶模型的效果相对较好。与普通混凝土单一试验数据的对比分析表明，修正分数阶模型对混凝土耗能频率相关性的计算效果最好，与试验数据间的误差在50%以内。

表5 基于单一文献数据的黏弹性模型参数确定

(a) 计算结果对比

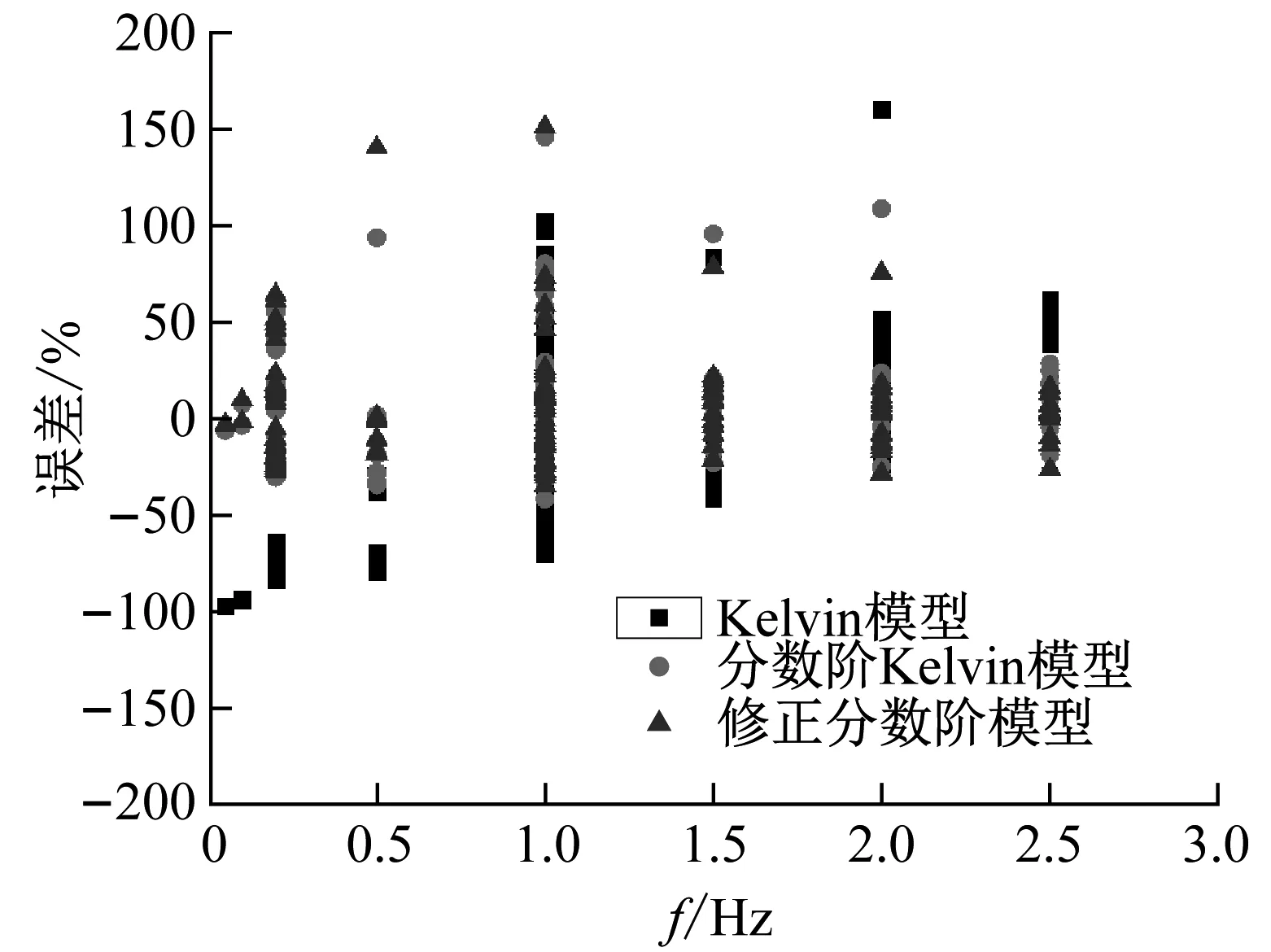
(b) 模型误差分析