超弹塑性泡沫连续冲击动力学行为分析的新方法

卢富德， 任梦成， 高 德， 奚德昌

(1.湖南工业大学 包装与材料工程学院，湖南 株洲 412007；2.浙江大学 航空航天学院，杭州 310027)

塑料泡沫由于其良好的缓冲性能、质轻、价廉等特点，常用于缓冲包装中。利用最大加速度-静应力曲线表征缓冲材料的缓冲特性是最基本且最常用的方法，在一系列缓冲材料厚度与跌落高度条件下，直接利用最大加速度与静应力曲线便可以计算出缓冲材料的面积与厚度两个尺寸参数[1]。通过最大加速度-静应力曲线得到的结构比较简单，对于复杂结构，一般通过试验手段得到缓冲材料应力-应变曲线[2-6]，然后利用一些特殊的数学函数对准静态应力-应变关系建立单轴本构模型[7-9]。在此基础上考虑应变率、密度等参数的作用，建立一个适用范围较广的本构模型，但是这些本构模型很少有考虑泡沫材料在卸载阶段的力学响应，因此也就不能适用于泡沫在受到加载-卸载-再加载-再卸载循环载荷时的情形下的力学性能预测。

文献[10]利用ABAQUS工具内置的弹塑性可压缩泡沫本构模型材料模型，分析了高密度聚乙烯泡沫加载-卸载力学行为；材料模型中利用线弹性卸载力学行为，但没有考虑卸载阶段的非线性行为。文献[11]利用ABAQUS工具的HYPERFOAM材料模型，并结合MULLINS模型，分析了EPP泡沫加载-卸载力学行为，此模型考虑了非线性卸载力学行为，并预测了泡沫超弹力学性能，但它没有预测实际所发生的残余应变。文献[12]介绍了LS-DYNA工具中MAT_LOW_DENSITY_FOAM(MAT57)模型， MAT57中的滞回卸载因子HU与形状因子SHAPE等效于ABAQUS中的MULLINS模型，MAT57可以表征具有非线性卸载行为，但同样不能预测实际发生的残余应变。文献[13]利用两个主流有限元工具ABAQUS与LS-DYNA中的本构模型，对EPS与EPE泡沫力学性能进行了一系列对比研究，结果发现实际泡沫力学性能是介于弹塑性力学性能与超弹性力学性能之间，既有残余应变，又有一定的超弹性，而两个有限元工具都不能完整分析泡沫复杂的卸载力学行为，尤其是残余变形的预测。

考虑残余应变影响以及非线性卸载力学特征，文献[14]分别建立了加载、卸载与再次加载本构模型，成功预测了泡沫连续多次冲击响应，但需要的试验次数较多，涉及到的参数较多。本文为塑料泡沫连续多次冲击力学行为提出新的计算方法，把一般性泡沫分解成两种典型泡沫力学性能:一个是弹塑性层，按照线弹性行为卸载;第二种是超弹性层，按照非线性方式卸载；通过两层特殊力学行为的叠置组合，进而达到简化连续多次冲击力学行为的目的。

1 泡沫力学本构模型基本理论

1.1 超弹性泡沫

超弹泡沫本构模型是基于应变能密度函数而提出的，代表性的应变能密度函数是Ogden提出的势函数，此函数U是3个主伸长量λ1,λ2与λ3函数，其数学表达式为

(1)

式中:μi,αi与βi为待识别常数;J=λ1λ2λ3。

在Ogden势函数中引入损伤函数即可得到Mullins效应本构模型的势函数，即

U(λ1,λ2,λ3,η)=ηU0(λ1,λ2,λ3)+φ(η)

(2)

损伤变量由式(3)给出

(3)

式中：r,m与β为材料常数;U0为卸载阶段的瞬时应变能;Um为卸载阶段的最大应变能。

式(1)～式(3)以超弹泡沫材料模型与马林斯模型植入有限元软件，分别对应有限元工具ABAQUS中的HYPERFOAM与MULLINS本构模型。由式(1)与式(2)所决定的应力-应变曲线示意图，如图1所示。式(1)中的参数能够表征线弹性阶段、应力屈服平台阶段及压实阶段等3个典型区域所围成的形状，式(3)能够表征非线性卸载行为。

对于单轴情形，其应力-应变关系为

(4)

对式(4)积分，即可得到式(3)的应变能U0

(5)

对应的最大应变能Um为

(6)

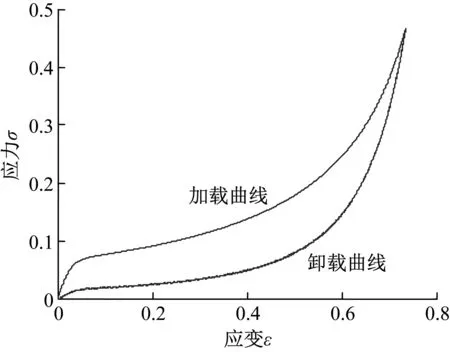
图1 超弹泡沫应力-应变曲线示意图

为了简化模型，在单轴情况，应力-应变关系可以表示为

(7)

式中,a1,a2,a3与a4为待识别参数。

对应的应变能U0变为

(8)

最大应变能成为

(9)

超弹泡沫一维本构模型，可以表示为以下形式

(10)

1.2 弹塑性泡沫

文献[6-8]利用有限元软件ABAQUS的弹塑性可压缩泡沫材料模型，对弹塑性材料EPS力学性能进行模拟，其加载曲线与图1的类似，示意图如图2所示，具有线弹性阶段、平台屈服阶段及压缩阶段，但卸载阶段是线弹性卸载，即有残余变形发生，这说明ABAQUS的可压缩材料模型不能模拟泡沫的非线性卸载行为。在单轴情况，弹塑性泡沫的本构模型可以表示为

(11)

图2 弹塑性泡沫应力-应变曲线示意图

1.3 超弹塑性泡沫

实际上，泡沫在卸载阶段既有非线性卸载特点，同时伴有残余应变的发生，如图3所示。把此问题看作是两层特殊本构力学行为串联形式[15]，示意图如图4所示。两层具有相同的横截面积但有不同的厚度，设两部分所具有的厚度分别是λh，(1-λ)h。两层具有相同的加载力学行为，但有不同的卸载力学行为。超弹层按照MULLINS效应规律进行卸载，弹塑性层按照线弹性规律进行卸载。这样既可以考虑非线性卸载，又可以表征泡沫实际变形中所产生的一定程度的残余变形。超弹塑性泡沫的超弹力学性能由式(7)中a1,a2,a3与a4等4个参数确定；其非线性卸载行为由式(3)的r，m，β这3个参数确定，线性卸载力学行为由式(11)第2个公式中的E确定，所以，基于超弹塑性泡沫应力-应变试验结果，识别a1，a2，a3，a4，r，m，β，E与λ等9个参数，即可完整表征泡沫的力学性能。

在确定两层材料本构模型后，可以按照图5所示的泡沫动力学模型进行动力学行为预测，动力学方程为

(12)

式中：M为物体的质量;x为物体的运动坐标;y为超弹层与弹塑性层分界线的运动坐标。

图3 超弹塑性泡沫应力-应变曲线示意图

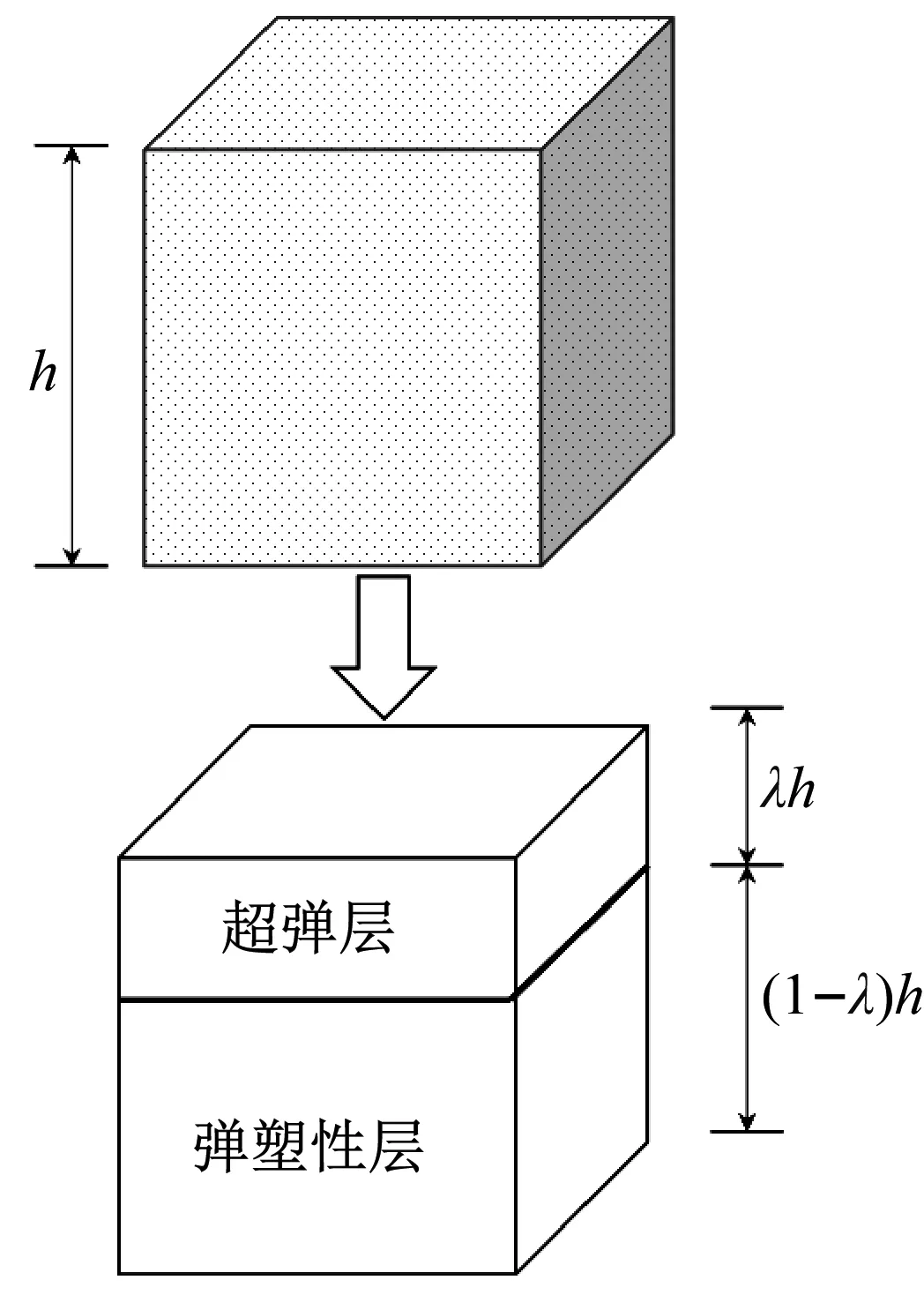
图4 泡沫力学性能等效示意图

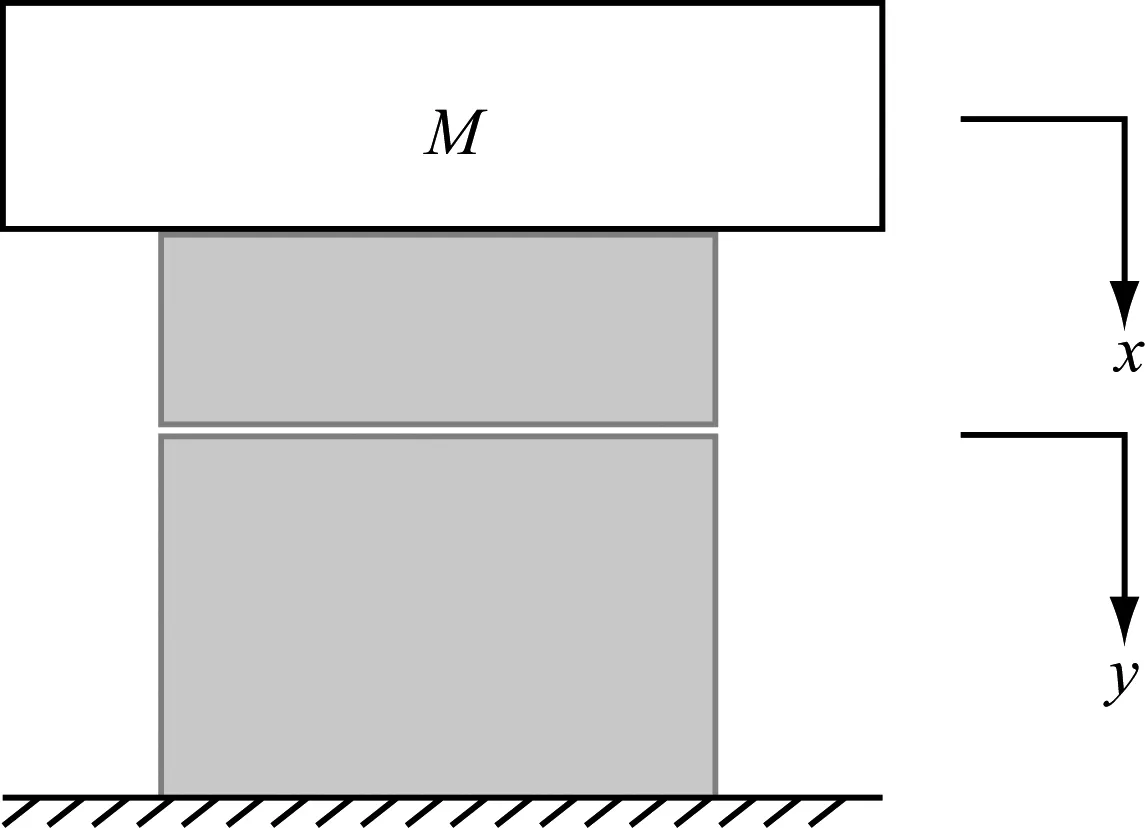
图5 泡沫动力学系统示意图

初始条件为

(13)

式中,H为跌落高度。

2 参数识别

2.1 试验方法

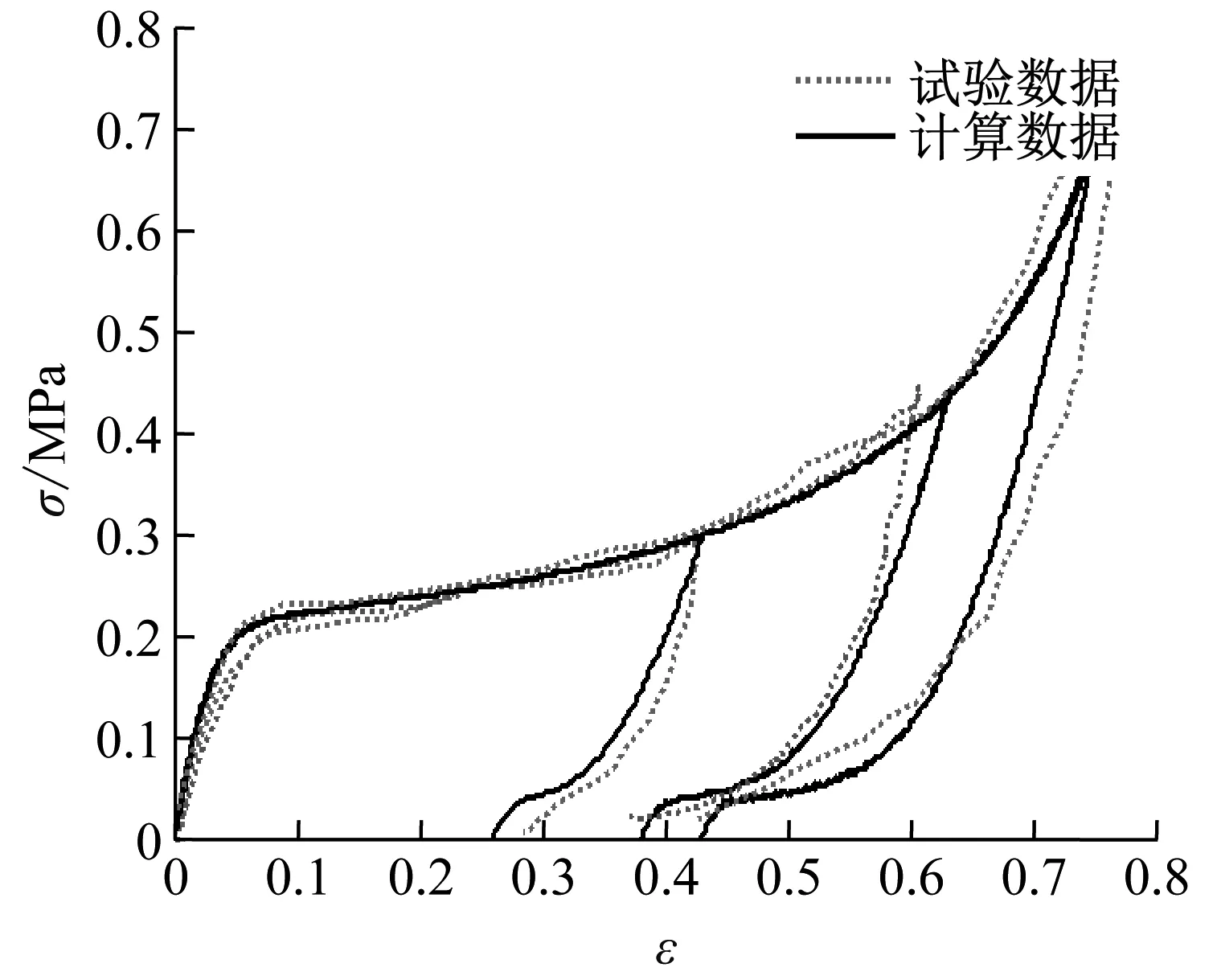
选取平均密度为28 kg/m3的EPS，尺寸：100 mm×100 mm×20 mm。因EPS具有率相关性，当用于缓冲包装中时，应变率大约在100 s-1，试验设备采用跌落塔，重锤质量为7 kg,跌落高度分别取0.3 m,0.5 m及0.7 m。利用加速度传感器得到加速度-时间曲线，结果如图6(a)中的虚线所示，然后得到图6(b)虚线所表示的应力-应变曲线。

(a)

(b)

2.2 参数结果

利用图6(b)中的加载曲线，利用最小二乘法识别出式(7)中的参数分别为：a1=0.21 MPa,a2=30,a3=0.096 MPa,a4=0.9；剩下的参数r，m，β，E，λ，是基于图6(b)中的卸载曲线并采用最小二乘法得到：r=1.2,m=0.003 MPa,β=0.5,λ=0.31，E=5.1 MPa。

利用得到的参数，求解振动方程式(12)，得到质量块的加速度-时间响应，如图6(a)中的实线所示，以及图6(b)材料应力-应变曲线。试验与理论结果对比，可以看出二者具有较好的吻合性。

3 连续跌落冲击行为预测

3.1 连续跌落动力学方程

根据振动方程式(12)，得到系统在第1次跌落高度H1条件下的冲击加速度-时间历程，并得到弹塑性层的残余应变为

(14)

由两层材料的变形路径示意图如图7所示可知，第2次跌落情形，超弹模型可以表示为

(15)

其中

(16)

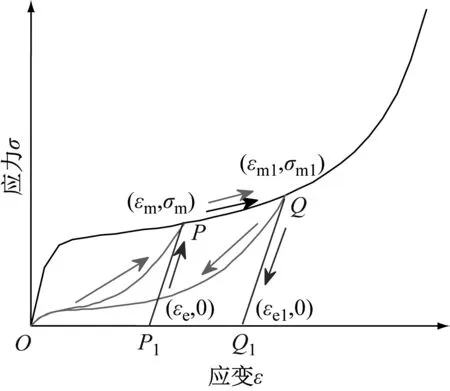
图7 第2次冲击时两层材料变形路径

第2次跌落，弹塑性模型可以表示为

(17)

第2次跌落冲击条件下，系统动力学方程为

(18)

初始条件为

(19)

重复以上步骤，可以求解泡沫在第3次及以后的连续跌落冲击条件作用下的加速度响应。

3.2 连续跌落动力学行为结果

采用参数h=0.04 m,M=8 kg,H1=H2=H3=0.6 m,得到物体在相同跌落条件下连续3次冲击的加速度-时间曲线结果，如图8中的实线所示，可以看出理论计算能够很好地吻合试验结果(如图8中的虚线)。

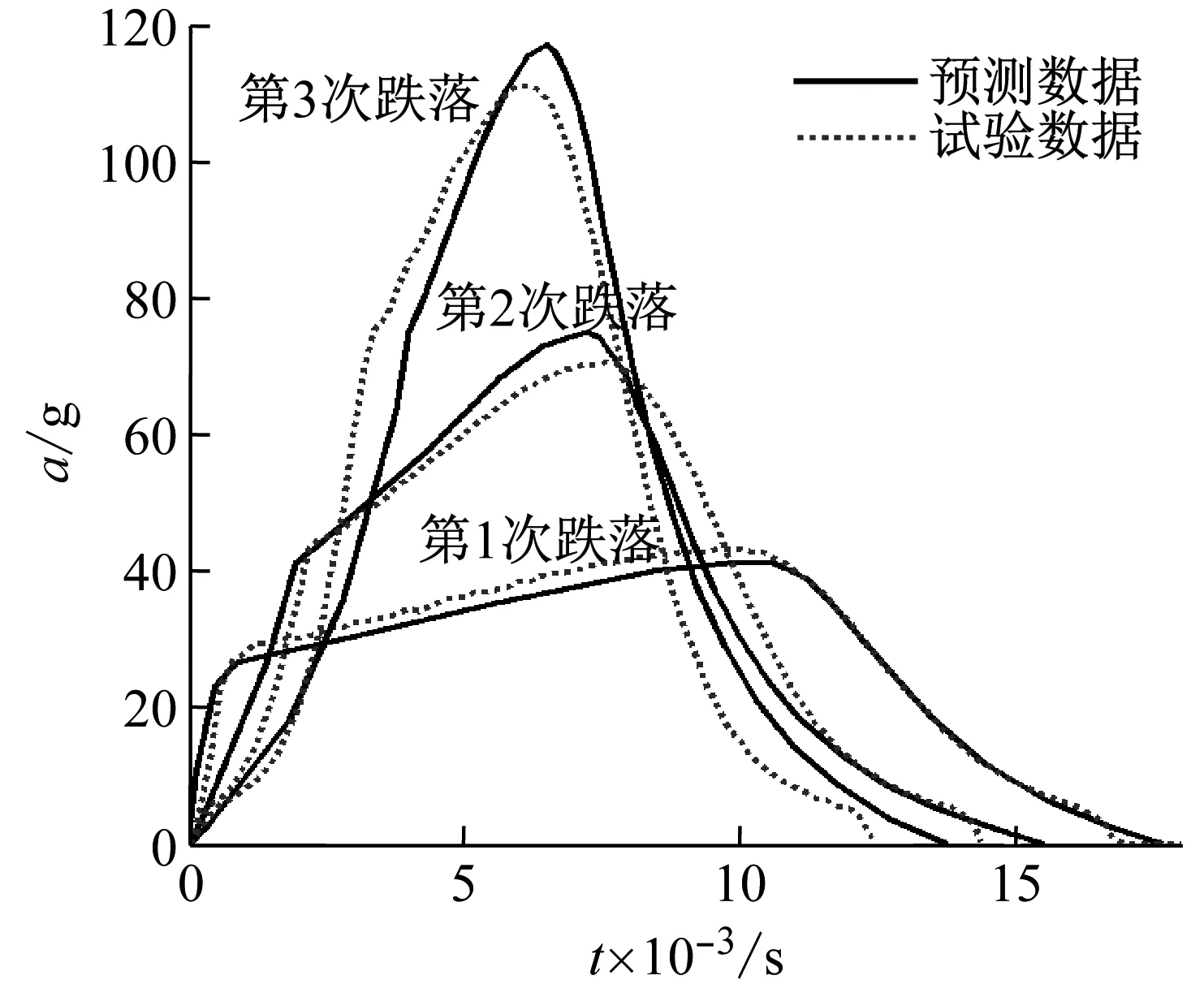
图8 连续3次相同跌落条件下加速度-时间曲线理论与试验结果对比

采用参数h=0.03 m,M=8 kg,H1=0.4 m,H2=0.5 m,H3=0.6 m,得到物体在不同跌落条件下连续3次冲击的加速度-时间曲线如图9中的实线所示，可以看出，除了第3次冲击有较大误差外，其余两层均具有较好地吻合性。第3次误差较大原因：第3次冲击时，最大压缩应变达到0.83，这已经进入泡沫的压实阶段，这个阶段的应力会急剧上升，因此会导致较大的误差。

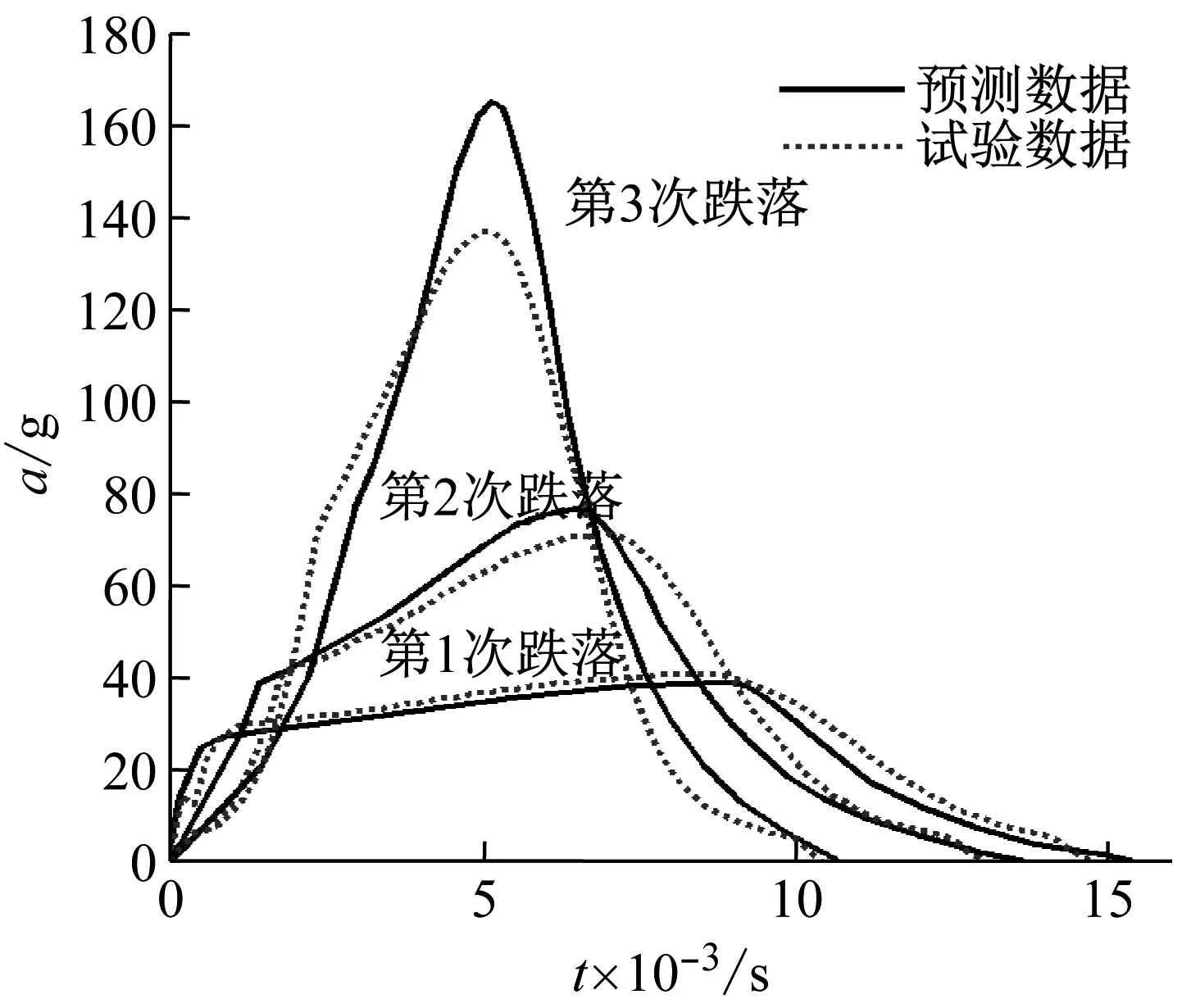
图9 EPS连续3次不同跌落条件下加速度-时间曲线理论与试验结果对比

4 结 论

本文把泡沫看作是由超弹层与弹塑性两层叠置而成，对泡沫力学复杂非线性行为计算提出了新的方法。利用双曲正切函数与双曲函数组合，表征了两层相同的加载力学行为。超弹层按照MULLINS效应规律进行卸载，弹塑性层按照线弹性规律进行卸载。采用单轴力学试验，识别了28 kg/m3的EPS泡沫超弹本构模型与弹塑性本构模型中的参数。从连续3次跌落冲击力学行为可知，3次加速度-时间曲线具有不同的形状，随着跌落次数的增加，加速度峰值越来越大，这是由于EPS泡沫残余变形所导致的力学性能变化引起的。

通过对比物体在3次连续跌落条件下的加速度-时间曲线的理论结果与试验结果，验证了本文所提出的计算方法的可靠性。