换元思想方法的应用举例

◎杨婷梅

(广东茂名幼儿师范专科学校理学院,广东 茂名 525200)

一、引言

换元法，又称变量代换法，是通过等式替换，把某个式子或变量看成一个整体，引入新的变量，把所要研究的数学问题转化为新的数学问题去研究，即把复杂的、非标准的问题变得标准化、简单化，从而使问题更容易得到解决换元法实质上就是利用“转化与化归”的数学思想，其关键是通过构造元和设元，把分散的条件联系起来，把隐含的条件显露出来，把条件与结论联系起来，把难以求解的形式转变为熟悉的形式，实现等量代换，使计算问题简单化，从而快速解决问题

因此，换元法是中小学数学，乃至大学数学中一种非常重要而且应用广泛的思想方法笔者研究了换元法在《数学分析》中的主要几点应用以及解题技巧，把理论知识和实际应用结合起来，培养学生的求异思维、发散思维和创新能力，提高解题效率，培养学生的数学思维和数学素养

二、换元法在函数极限中的应用

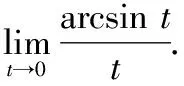
令=arcsin，

则=sin且当→0时，有→0

【评析】可以发现，当→0时，arcsin与是一组等价无穷小，通过换元可将其转化为第一类重要极限问题

令=tan，

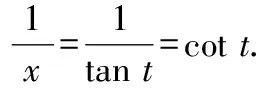
当→0时，有→0

【评析】以上两个例子使用换元法，把极限问题转化为熟悉的两类重要极限问题来计算，使复杂的问题简单化

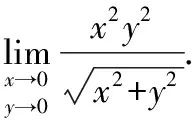
设=cos,=sin,∈[0,2π]

当→0,→0时，有→0

于是，

【评析】该例题通过三角换元，把二元函数的极限问题转化为一元函数的极限计算，减少了一个变量计算更方便简洁

三、换元法在求解导数和微分问题中的应用

在计算函数导数与微分问题时，换元思想方法同样适用，它是求解复合函数导数和微分的重要思想方法

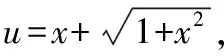
四、换元法在计算积分问题中的应用

函数积分是大学课程《数学分析》中的重点内容，同时也是数学专业学生难以掌握的知识点之一使用换元法，可以快速解决一些复合函数的积分问题，通过变量代换，把一个不能直接运用积分公式计算的积分问题转化为可以用积分公式来计算的问题，它在计算函数不定积分中的应用主要分为以下两种情况

(一)不定积分的第一换元积分法

第一换元积分法实质上是将不定积分的被积表达式“凑”成微分的形式，简称为“凑微分法”，但不能忘记最后要还原回原来的变量熟练换元法后，可以不写出中间的换元过程

令=7+3，则有

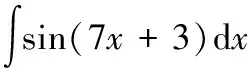
【评析】当不能直接利用积分公式

(二)不定积分的第二换元积分法

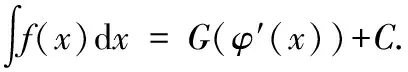
第二换元积分法的关键在于如何构造一个恰当的变量代换，以达到积分的目的

不妨设=5sin，有d=5cosd

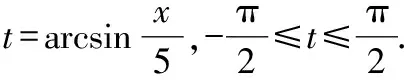
于是，

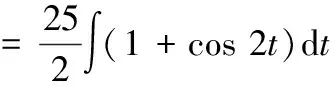
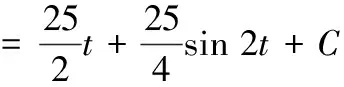
(三)用换元法求解定积分

设=5sin，有d=5cosd

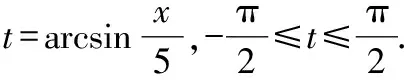
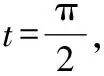
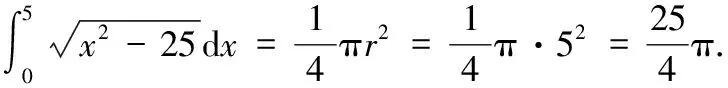
(四)极坐标系下二重积分的计算

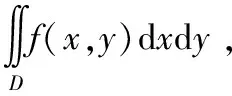
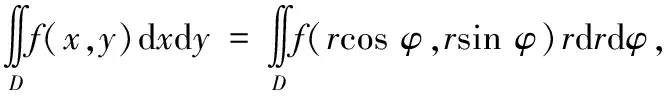
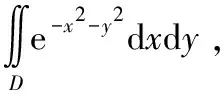
【评析】用极坐标变换求二重积分时，要注意除变量作相应的替换外，要把“面积微元”dd换成dd

五、换元法在幂级数中的应用

设有数列{}(=1,2,…)，称函数项级数

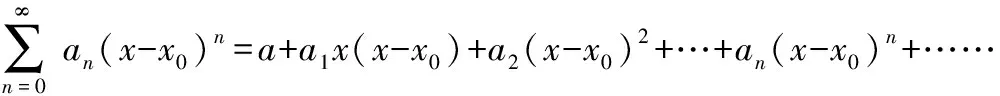
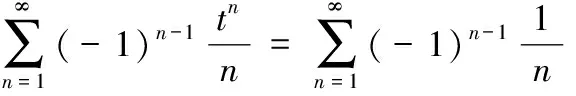
由于=-2，故=+2，于是得到幂级数

【评析】本例题若不用换元法，使用比值法求解收敛半径，计算比较烦琐，通过换元，把非标准型的幂级数转化为标准型的幂级数，更容易求出收敛半径和收敛域

六、结语

以上求极限问题，应用换元法，可以把复杂的极限问题转化为两个重要极限问题进行计算，或者减少极限变量，把含有两个变量的极限问题转化为只有一个变量，使问题简单化；微分、不定积分或定积分问题使用换元法，可使计算简单快捷；非标准型的幂级数的收敛性问题用换元法可转化为标准型的幂级数来讨论

换元法可解决以上相关的数学问题，可见换元法在大学《数学分析》课程中的应用非常广泛与普遍，对于学生来说，熟练掌握且灵活应用换元法是非常重要的学生通过运用换元思想使问题简单化，这为解决复杂的数学问题提供了重要的解题思路，提升了解题速度，培养了学生的数学素养与思维品格