“深度学习”教学模式下的一堂好课——以八年级下册“平均数”为例

◎王文义 何 男 朱惠英

(南宁师范大学 数学与统计学院，广西 南宁 530100)

一、问题的提出

(一)提出问题

自从《普通高中数学课程标准(2017年版)》提出了数学核心素养，广大教育者们都开始转变传统的教学观念，探索新式的教学法过去以教师为中心、灌输知识的时代已经不能适应现代社会的需要教师应当构建真实的情景，给学生提供创造的机会，使数学知识与实践相结合，让学生真正从“学会知识”跨越到“学会学习”Ference Marton和Roger Saljo在1976年率先提出“深度学习”的相关概念，自此深度学习理论开始不断补充和完善它究竟“深”在何处？与传统教学有什么区别呢？下面通过吴老师的一堂好课来感受深度学习教学模式的魅力

二、“深度学习”的内涵

(一)“深度学习”的定义

“深度学习”是指主动的、探究式的学习，要求学习者积极主动地建构知识，把所学习的知识转化为技能并迁移应用到现实情景中来解决问题，从而促进学习者认知能力、问题解决能力、批判性思维、创造性思维等数学能力的发展

(二)“深度学习”的特点

第一，“深度学习”强调教师要创设真实的数学情境，引导学生主动参与数学活动，使学生亲自发现知识、寻找知识，像当年科学家一样总结出知识的概念，形成丰富的内心体验教师要将数学的思想和方法、考虑问题的策略和辩证的思维渗透到数学活动的探究中

第二，“深度学习”强调对教学内容的结构化，帮助学生系统掌握知识的内在联系

第三，“深度学习”强调知识的应用性，培养学生数学建模的能力，让学生能将所学的知识真正运用于解决真实问题

第四，“深度学习”强调要帮助学生树立正确的人生观和价值观，将德育渗透到教学过程当中学生在数学活动的过程中潜移默化地形成了正确的价值观，提高了品德修养，继承了中华民族优秀的传统文化

三、名师课堂

(一)情景构建，激发兴趣

1情景构建

教师：你们看过音乐类综艺吗？你们喜欢里面的谁啊？

学生：看过，有很多喜欢的歌手

教师：我真的很喜欢看音乐类综艺，因为这让我想起了当年的我，曾经的校十大歌手(吴老师展示唱歌图片)

学生：哇哦

教师：我印象最深刻的是我和我的好朋友的那场晋级赛，竞争非常非常激烈我把当时的数据收集、整理，并用熟悉的表格描述了我们的技巧分和情感分(见表1)综合这两项成绩，你觉得谁将会获得晋级资格？

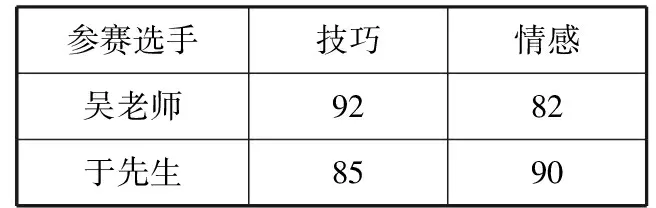
表1 参赛分数

学生：我认为于先生会胜出因为于先生的平均分比吴老师高

教师：怎么算出来的呢？

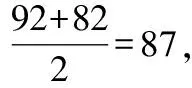
教师：平均数运用得真好，你能通过这两个算式总结出计算平均数的一般方法吗？假设有个数据,,…，怎么计算它的平均数呢？

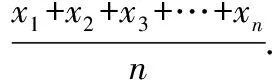
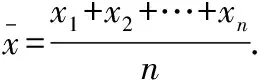
学生：两个式子的结果相同，但形式不同

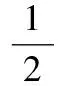
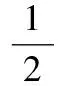
教师：这名同学回答得非常好，懂得从数据的重要程度去分析问题这种变形说明，我们利用平均数计算平均成绩时，每一个数据同等重要那你觉得谁将获得晋级的资格？

学生：于先生

教师：大家异口同声地告诉我，我的朋友获得了晋级资格但是我晋级了决赛，是我而不是他，这是为什么呢？

学生：可能是技巧分占的比重比较大，情感分占的比重比较小

教师：接下来小组合作，根据表1设计出符合当时选拔情况的方案

2评析

吴老师通过引入自己参加歌手大赛的场景，给出数据让学生分析谁能进入决赛，既锻炼了学生的数据分析能力，又激起了学生的好奇心在分析数据的同时，学生总结出了求平均数的计算方法当所有学生都认为吴老师被淘汰时，吴老师却说自己最终进入了决赛，激起了学生的兴趣吴老师抓住了学生心理，让学生进行小组合作，充分发挥想象力，设计出与当时场景相符合的方案这充分体现了“深度学习”强调引导学生主动参与学习活动，亲身经历知识发现、发生、发展的过程，形成丰富的内心体验的特点

(二)引权入课

1探索问题，发现“新”知

小组A：技巧在晋升比重中占60%，情感占40%，吴老师分数为92×60%+82×40%=88，吴老师的朋友的分数为85×60%+90×40%=87吴老师就可以晋级了

教师：第一个问题，你们这样设置的想法是什么？

小组A：将整体看成100%，因为我们比较看重技巧，所以就给技巧的占比大一点

教师：第二个问题，你们计算的依据是什么？

小组A：技巧的占比为60%，所以要用技巧的分乘60%；同理，用情感的分乘40%，两部分相加为得到的分数

教师：很好，第一个方案已经可以让我晋级了，有请第二个方案

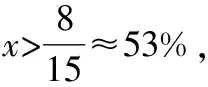
教师：非常好，请坐还有其他的方案吗？

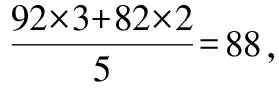
教师：你们的计算又依据了什么？

小组C：一共有5份，技巧分占了3份，情感分占了2份除以5，这个5是总份数

教师：你们设计的方案太棒了！你们所设计的方案跟当时比赛的方案大同小异，都是更侧重技巧成绩对于技巧和情感这两个不同类型的数据，我们分别赋予了60%和40%这样的比重那么这时我们称60%为技巧成绩的权，40%是情感成绩的权如3是技巧分的权，2是情感分的权权有表示重要程度的意思

2用中国文化解释“权”的定义

教师：在古代，我们测重的时候用的工具叫杆秤(图片展示)，你们见过吗？在杆秤上有一个非常明显的铁疙瘩，它叫作秤锤，它就是权而且我国著名的教育家孟子在他所著作的《孟子·梁惠王上》提道：“权然后知轻重”孟子说权是表示重要程度的意思如此重要的权结合了平均数的计算，我们就有了一个叫作加权平均数的概念

教师：请同学们认真观察你们所提出的方案，思考1:请用符号语言表示计算加权平均数的一般方法还是有个数据,,…，每个数据所对应的权为,,…，你们能用它表示出加权平均数的一般方法吗？

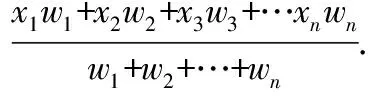
教师：我想知道你是怎么得到这个公式的？

学生：每个数据都有对应的份数，这个份数就是权每个数据乘权得到该项目的得分，把所有数据的得分加起来除以总份数就得到加权了平均数

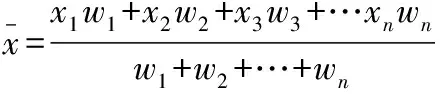
3点评

学生在设计方案的过程中充分发挥了自己的想象力，创造性地提出了自己的方案吴老师将知识技能、数学思考、问题解决、情感态度四个方面有机结合，发扬了教学民主，让每个学生都积极主动地参与到数学活动中来，让学生通过数据分析发现数据的重要程度，由重要程度引出权的概念，再让学生通过自己设计的方案，总结出加权平均数的数学表达式这一过程体现了由特殊到一般的数学思想，提高了学生的归纳概括能力，让学生在问题解决中潜移默化地学会了如何计算加权平均数教师将中国历史文化渗透到教学中，让学生既能深刻理解所学知识的概念，又增强了民族自豪感

因此，“深度学习”教学既要注重知识的广度，又要注重知识的深度和知识与知识之间的联系，形成知识网络教师在教学中应当采用蔡元培先生的文理融合思想，将各门学科知识融合为一体，可以用文科的知识来促进理科的学习，也可以用数学思维和方法来解决各类问题“深度学习”教学提倡将品德、中国文化和数学思想渗透到教学中，让学生在学习知识的过程中将知识作为“精神种子”发育成为个体的智慧、思想和美德教师要将知识作为“精神种子”播种在学生身上，创设良好的情景，精心地照料，最终转识成知、转知成智，化知识为美德

(三)实战应用

1定权招贤

教师：加权平均数不仅可以让我晋级决赛，还可以在我们生活中的很多方面更好地招贤纳士有一家跨国公司计划招聘1名英语翻译，甲、乙两名应试者都报名参加了应聘，进行了听、说、读、写的英语测验，他们的每项成绩(百分制)如表2所示

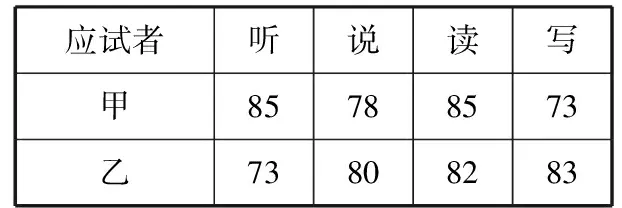
表2 英语水平测试

如果公司想招一名综合能力较强的翻译，请计算甲和乙的平均成绩，从他们的平均成绩来看，应该录取谁?

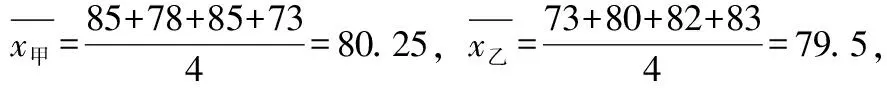
教师：非常好，书写也非常工整如果公司想要招聘一名笔译能力较强的翻译，你认为应当制订什么样的规则呢？

学生A：写最重要，写占40%，剩下的求平均分

学生B：读和写都很重要，读和写占的比例都是40%，听和说的比例占10%还有其他不同意见吗？

学生C :对于笔译能力来说听也很重要因为会听才会读和写

教师：我觉得你说得有道理，在上一名同学的基础上改，你觉得应该怎么改？

学生C：写最重要，读第二重要，听第三重要听、说、读分别占20%、10%、30%，写占40%

教师：你已经完全说服了我，我们来看看公司的方案2∶1∶3∶4，这个公司“盗用”了你的方案因此，我们在设计方案时不能只考虑一个因素，也要考虑其他因素下面我们按照这个比例，来计算甲和乙的成绩，看这一次究竟会录取谁

2思考与归纳

教师：基于上面两问，你能体会到权的作用吗？

学生：权体现了数据的重要程度权可以影响平均数的计算结果

教师：通过刚才的招贤纳士，我们对权有了更深入的理解接下来思考，简单形式的平均数和加权平均数有什么区别，又有什么联系呢？

学生D：简单形式的平均数，每个数据的重要程度都相同加权平均数，每个数据的重要程度可能会不同平均数的计算需要除以数据的个数，加权平均数需要除以权的和

吴老师给出了表格，让学生回答表格中的内容(见表3)

表3 区别和联系

学生们争相举手回答问题最终一名同学说出了正确答案：当===…=时，加权平均数就变成了简单形式的平均数

教师：也就是说简单形式的平均数是加权平均数的特殊情况

3点评

学生在学习权的概念之后，运用所学的知识来解决实际中的问题，体现了数学与生活息息相关，生活离不开数学吴老师创设情景，让每名学生都大胆地提出招聘方案，不断补充，最终形成了完美的方案在这一过程中，学生充分发挥了创造性思维，提高了数据分析能力通过归纳总结加权平均数与简单形式的平均数的区别和联系，学生对概念更加清晰了，形成了知识链，潜移默化地提高了归纳概括能力踊跃的发言也提升了学生的数学语言表达能力

(四)为权做思，课堂小结

吴老师以问题串的形式来回顾这堂课所讲授的内容，提出了以下问题：

1如何计算一组数据的加权平均数？

2权的形式和作用分别是什么？

3谈谈你对所学统计知识的认识？

最后，吴老师引用爱迪生的一句话：天才是百分之一的灵感，加百分之九十九的汗水用加权平均数来理解就是：聪明重要，但努力更重要吴老师深入挖掘深度学习的素材，用权的知识成功解释了勤奋努力才是成功的决定性因素，体现了育人与育才相结合，品德与知识相融合，既复习了权的知识，又培养了学生正确的奋斗观念

四、如何基于“深度学习”模型进行教学

(一)教学中要挖掘知识的深度和广度

“深度学习”既要注重知识的深度，又要注重知识的广度知识与知识间的联系，形成知识网络教师在教学中应采用蔡元培先生的文理融合思想，将各门学科知识融合为一体，可以用文科的知识来促进数学的学习，也可以用数学的思维来解决各类问题

(二)在教学中培育学生的数学思想

“深度学习”要求教师在课堂中培养学生的数学思想，在传授知识的同时创设情境，让学生真正体会到知识点背后蕴藏的数学思想就像吴老师要求学生从自己设计的方案中归纳出加权平均数的数学表达式，充分体现了从特殊到一般的数学思想数学思想可以让一个人的精神得以升华，从更高的角度和视野来看待问题数学思想需要长期的培养，教师要深度挖掘数学思想的素材，让学生在学会知识的同时，潜移默化地体会到数学思想的魅力

(三)知识即是美德，化知识为美德

学生学习知识的过程从根本上说是知识作为“精神种子”发育成为个体的思想、智慧和美德的过程教师要将知识作为“精神种子”在学生身上展开精神发育过程，转识成知、转知成智，化知识为美德教师设计教学时必须思考学生掌握了哪些知识，掌握了哪些数学素养，培养学生哪些高尚品德品德教育与学科精神相互融合的课堂，才是真正的育才胚土