基于多元线性回归模型的赤峰市用水量预测与分析

刘 冬

（赤峰学院 数学与计算机科学学院， 内蒙古 赤峰 024000）

1 引言

伴随着我国国民经济的快速发展以及人口的迅速增加，人民的生活水平有了质的飞跃，城市生活用水和工业用水的需求也随之增加，城市中供水匮乏的问题日益突出。城镇用水量的准确预测是城市供水系统规划、设计和运行的重要依据，对城市的未来发展具有重要意义。通常对用水量的预测一般采用经验类推的方法，如综合指数法、平均增长率法，可以得到较好的结果。 在向经济型城市发展的进程中， 城市水资源的利用高度依赖于人的活动， 市场中的各项资料以及数据的变化是不规律的，与历史资料比较也不能达到预期的效果。 因此目前城市用水量预测的方法主要有定量预测、回归分析法及灰色预测法[1]。 运用所学的spss 软件，在多元线性回归分析的基础上，根据数据构建出赤峰市城市用水量的预测模型。多元线性回归法不但需要考虑到回归的系数， 还要考察预测和假设性检验，考虑独立变量之间的关系以及是否存在共线性的问题。为了更好地解决赤峰市城市用水量预测模型中存在的共线性问题，提高城市用水量预测的精度，本文采用了多元线性逐步回归方法对模型进行了检验。

2 多元回归分析原理

在日常生活中，当我们需要对某一个因变量进行统计分析的时候，往往会有一个或着多个自变量来影响这个因变量。所以当我们建立回归方程的时候需要考虑k 种自变量x1,x2,…,xk和因变量y 之间的关系：

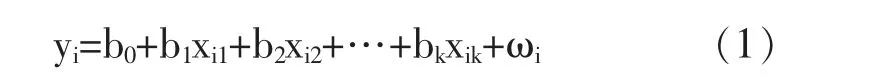
这个式中：

b0,b1,b2,…,bk是需要进行参数估计的回归系数；

i=1,2,…,m（n 表示样本容量）；

ωi是随机误差。

我们假定随机误差ωi服从来自总体分布N(0,σ2)的独立同分布。 用最小二乘法的方法在X,Y 两个观测样本下估计b0,b1,b2,…,bk，这样我们可以以矩阵的形式写出回归方程。

矩阵表示的多元线性回归模型为：

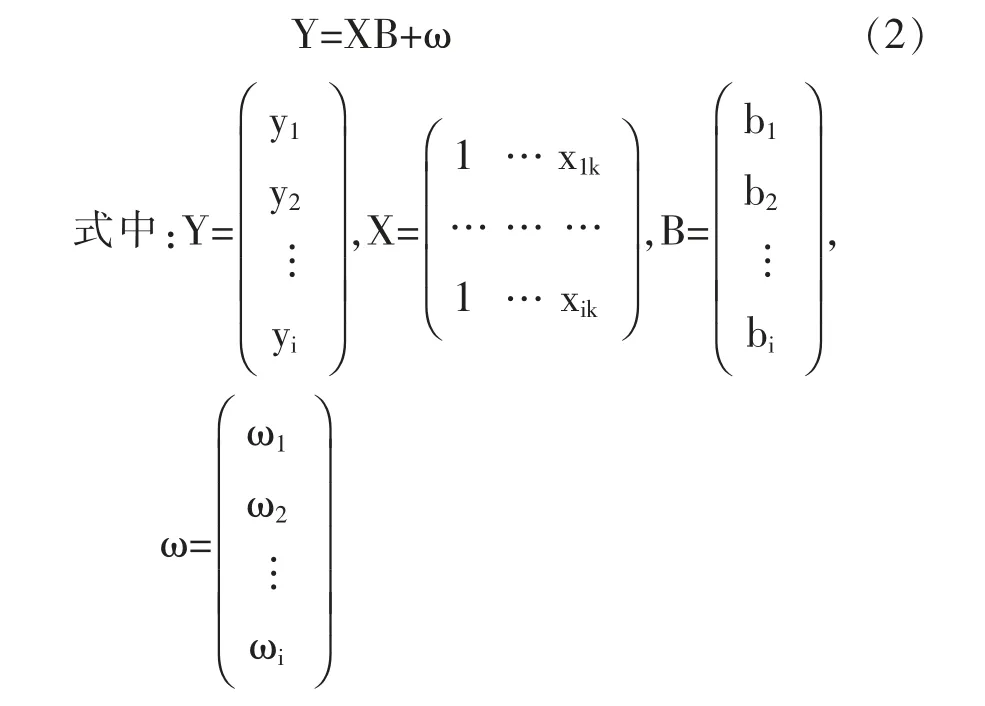
Y 为因变量观测值的向量；B 为参数向量；X为自变量向量；u 为随机误差向量。 采用最小二乘法估计法估计总体参数，其估计量为B=(b0,b1,…,bk)的转置。

用F 统计量对回归方程进行显著性检验，记：

式中：

如果F 统计量的P<0.05， 则回归方程通过了显著性检验，即方程具有统计学意义。 用T 统计量对回归系数进行显著性检验。 记：

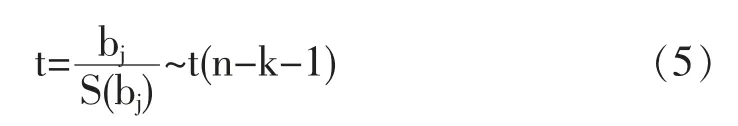
如果T 统计量的P<0.05， 则回归系数通过了显著性检验，即系数具有统计学意义。

3 城市用水量SPSS 回归分析及结果检验

有许多因素影响城市用水。选择若干个影响城市用水量的因素，如表1 所示，这些影响城市用水量的因素是根据 《赤峰市统计年鉴2010-2019》和《赤峰市水资源公报2010-2019》所确定的。其中，x1是国内生产总值(万元)，x2是人均国内生产总值(万元)，x3是固定资产投资(万元)，x4是工业增加值，x5是城镇人口总数（万人），x7是工业用水(104m3/a)，x8是人均日用水(L)，Y 是总用水量(104m3/a)，建立预测赤峰市城市用水的数学模型。

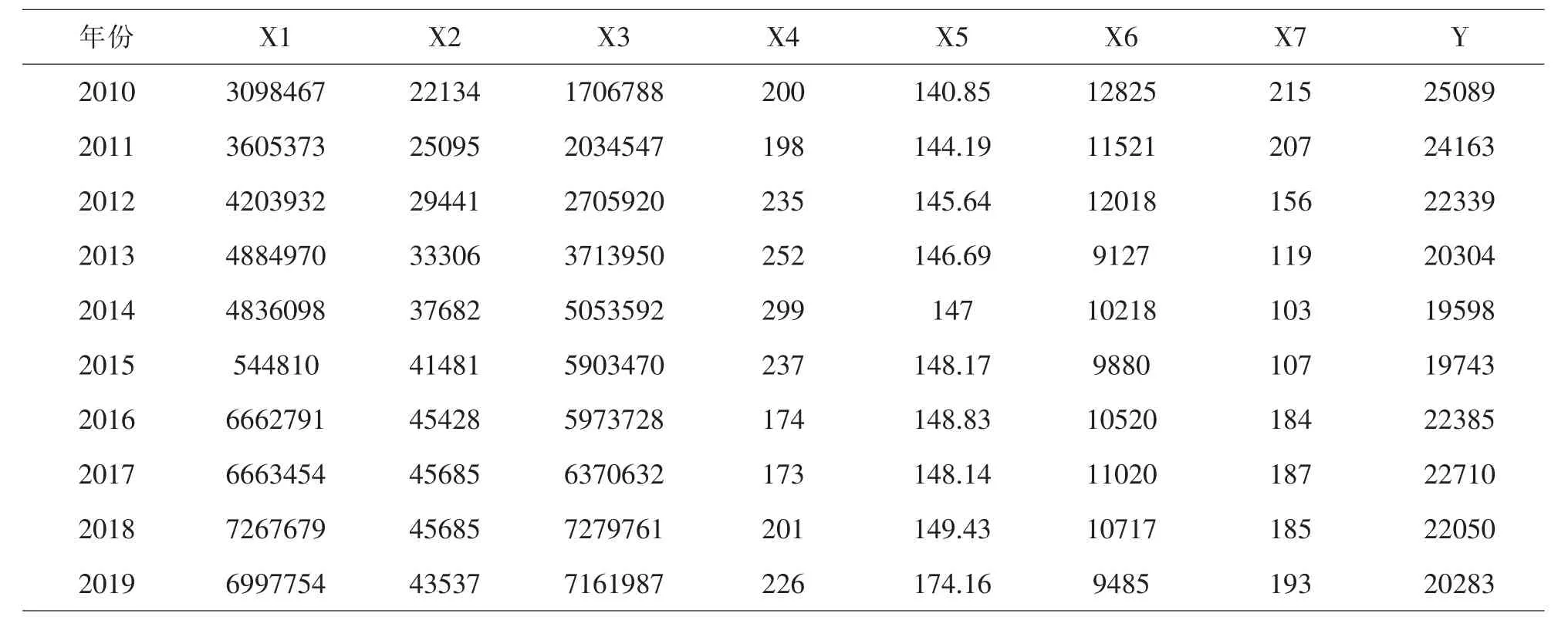
表1 城市用水量及其影响因素的基本资料

3.1 多元线性回归模型

做变量之间的相关分析， 用spss 得到相关系数矩阵

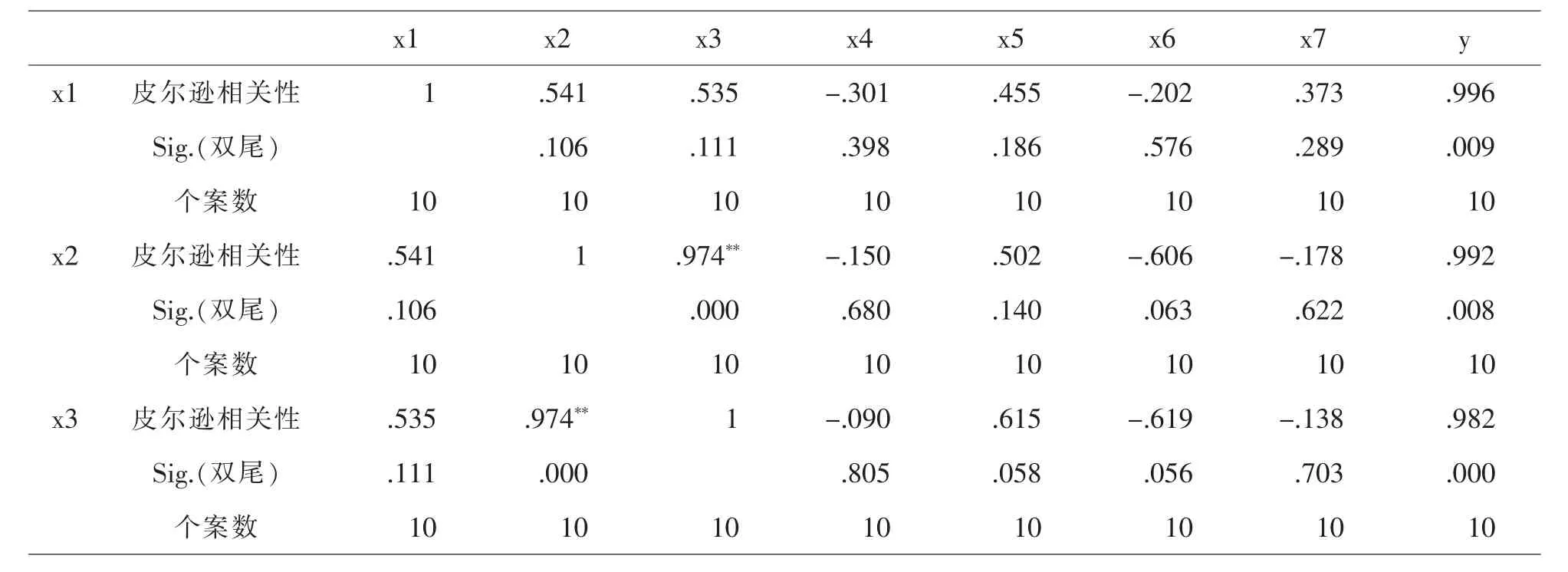
表2 相关性

从相关阵看出，y 与7 个自变量x1，x2，x3，x4，x5，x6，x7的相关系数都在0.8 以上，且p<0.05，说明所选自变量与y 有很强的线性相关，用y 与自变量做多元线性回归模型是适合的。

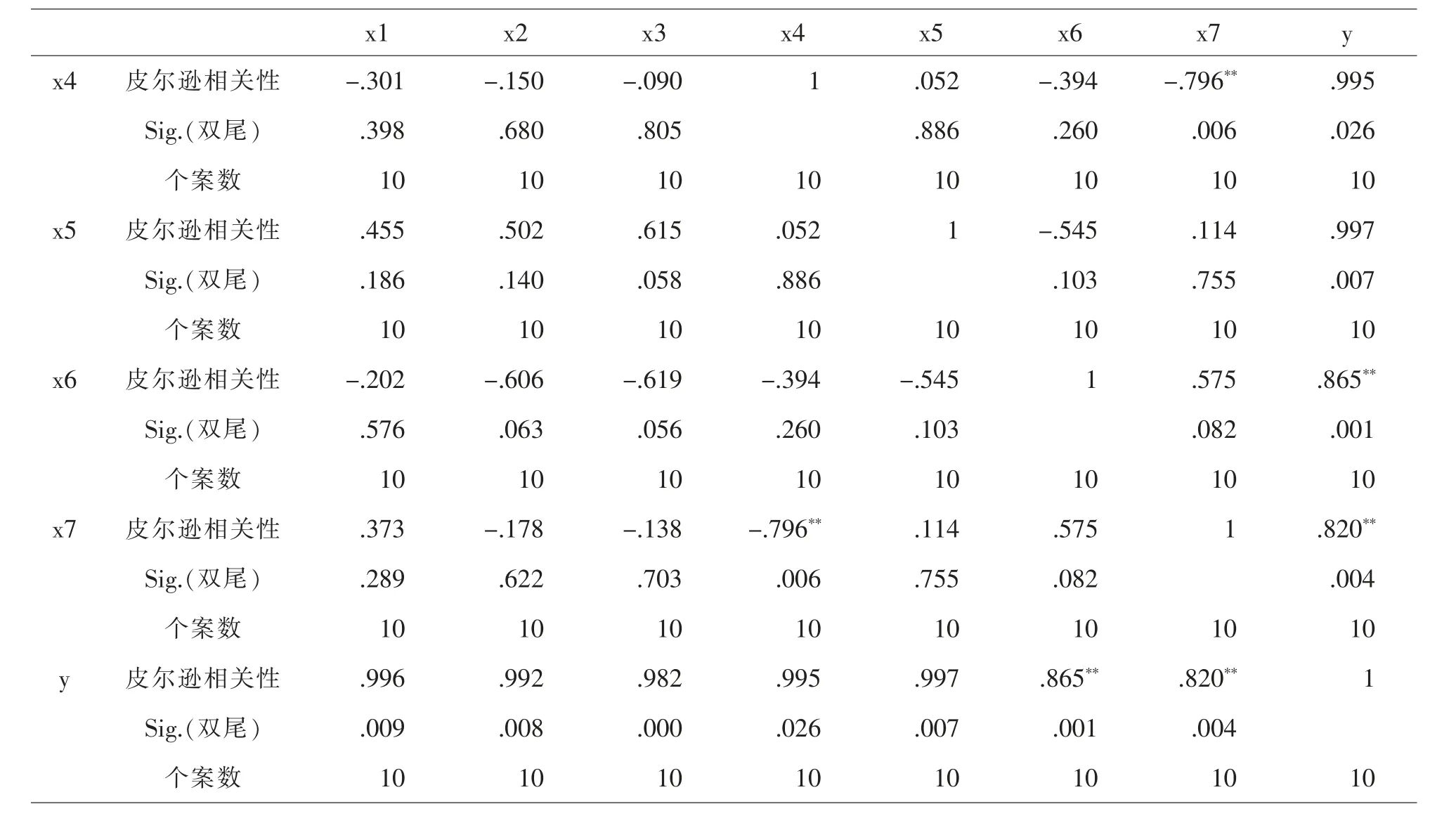
x1 x2 x3 x4 x5 x6 x7 y x4 皮尔逊相关性 -.301 -.150 -.090 1 .052 -.394 -.796** .995 Sig.（双尾） .398 .680 .805 .886 .260 .006 .026个案数 10 10 10 10 10 10 10 10 x5 皮尔逊相关性 .455 .502 .615 .052 1 -.545 .114 .997 Sig.（双尾） .186 .140 .058 .886 .103 .755 .007个案数 10 10 10 10 10 10 10 10 x6 皮尔逊相关性 -.202 -.606 -.619 -.394 -.545 1 .575 .865**Sig.（双尾） .576 .063 .056 .260 .103 .082 .001个案数 10 10 10 10 10 10 10 10 x7 皮尔逊相关性 .373 -.178 -.138 -.796** .114 .575 1 .820**Sig.（双尾） .289 .622 .703 .006 .755 .082 .004个案数 10 10 10 10 10 10 10 10 y 皮尔逊相关性 .996 .992 .982 .995 .997 .865** .820** 1 Sig.（双尾） .009 .008 .000 .026 .007 .001 .004个案数 10 10 10 10 10 10 10 10

下面用spss 对原始数据做多元线性回归分析：

表3 模型摘要

表4 ANOVAa

从回归的效果看，R 方=0.999， 说明回归效果很好。 用x1，x2，x3，x4，x5，x6，x7预测y 正确率可以达到99%以上。

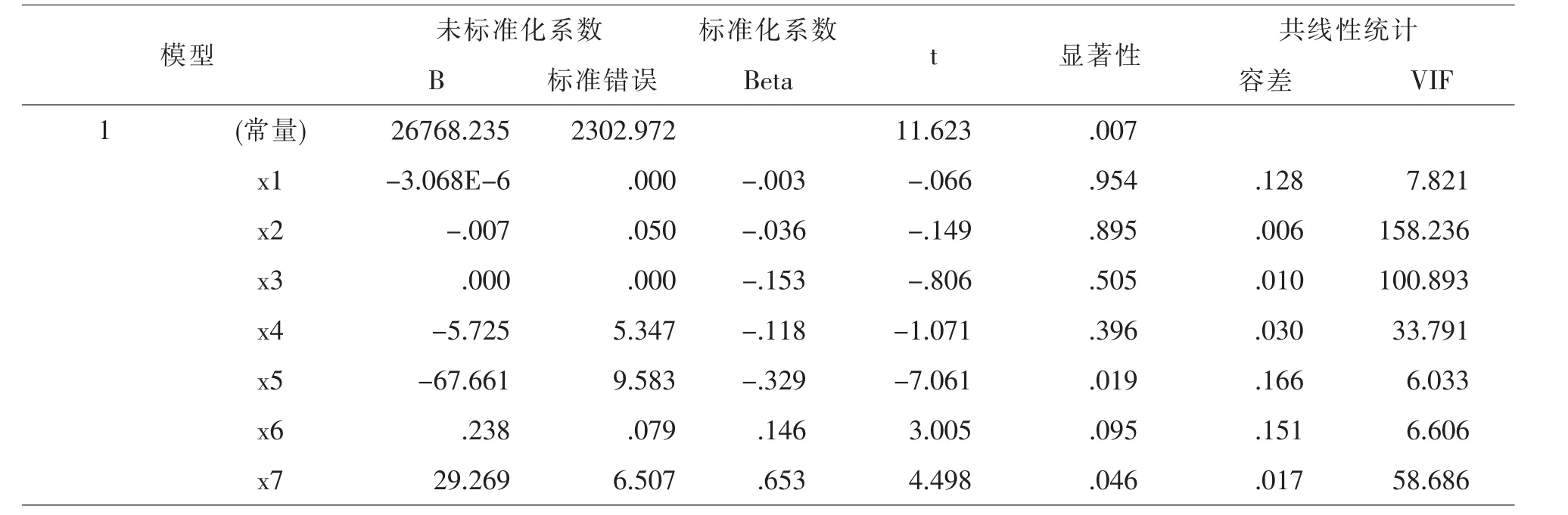
表5 系数a

从方差分析表，F 统计量的值为397.169，P值=0.003<0.05，表明回归方程有统计学意义。

回归系数的显著性检验， 自变量x1，x2，x3，x4，x5，x6，x7整体上对y 有显著影响， 但是x1，x2，x3，x4，x5，x6系数没有通过显著性检验。

在多重共线性的诊断中也发现有几个自变量的VIF 值大于10，说明存在严重多重共线性。

3.2 逐步回归分析的基本思路

在现实生活中，我们一般都会选择多个相对于因变量y 的具有重要决定性的变量，此时将这个变量称之为自变量，在生活中我们所研究的各种因变量和自变量之间的关系中， 可以使用多元回归分析，初步地创建一个由因变量进行预测分析的“最佳”的回归方程。 渐进式回归分析就是在此基础上发展起来的。 其基本思想是，在多元线性回归方程时，应分阶段进行自变量的选取，即每步选取一个自变量。 每一步都要进行F 检验，确保每次引入新的自变量，回归方程只包含显著的变量。 同时要保证引入自变量的显著性水平小于剔除自变量显著性水平。直到在回归方程中的变量都不能被剔除而又没有新的变量可以被引入时为止，这时逐步回归过程才算结束完成。

表6 中，多元线性逐步回归分析模型中第五个模型的调整R 方为0.998，是五个模型中调整R 方最大的。表明模型五中的自变量与因变量之间有良好的相关性。表明模型五的多元线性回归方程比较适合，即因变量Y 与所选的5 个解释变量x3，x4，x5，x6，x7线性关系非常密切。

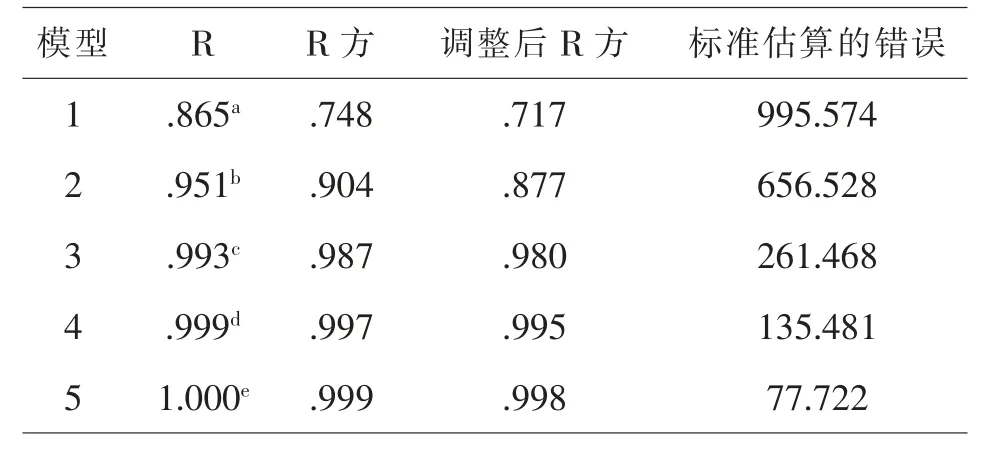
表6 模型摘要

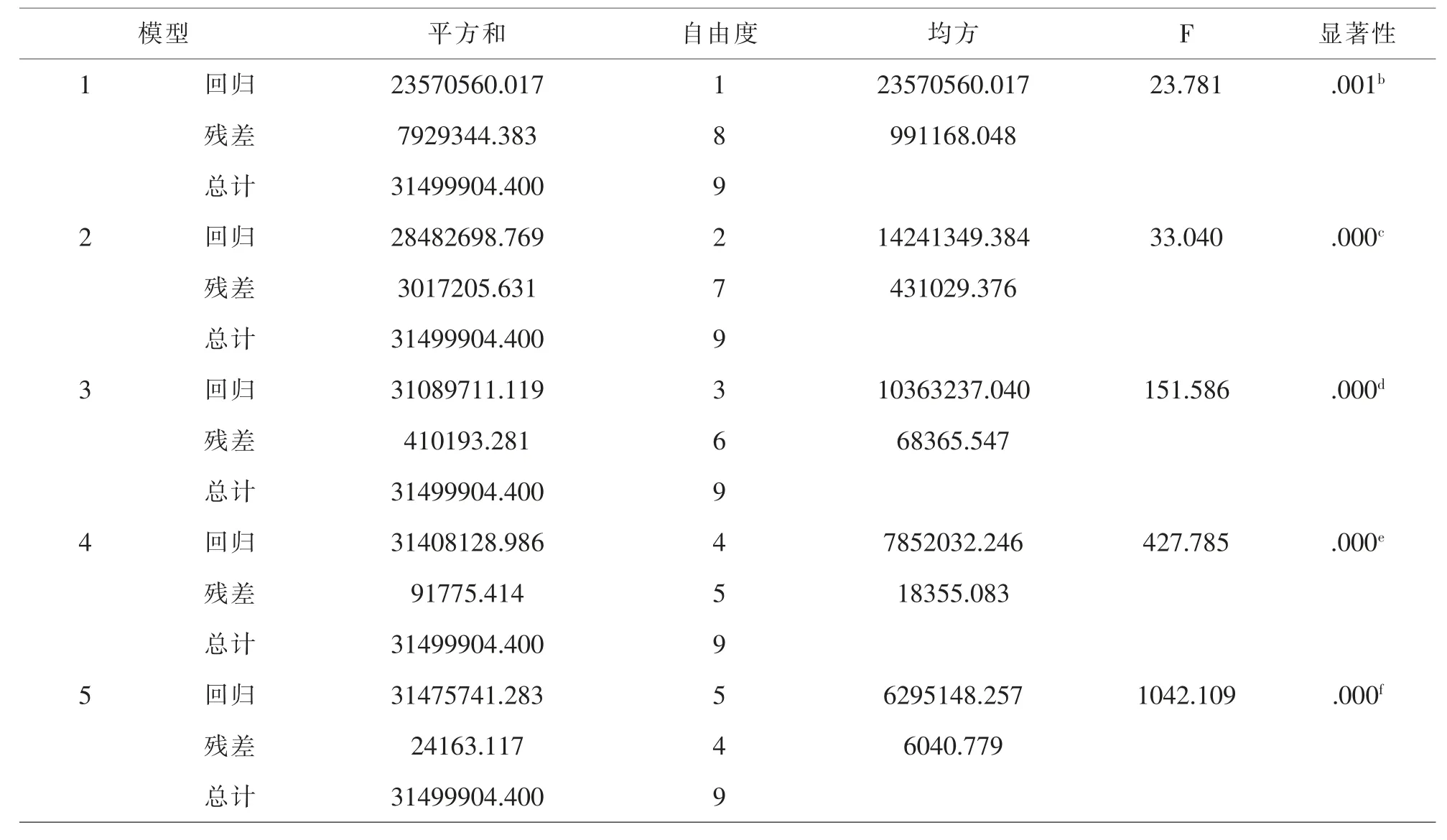
表7 ANOVAa

五个模型中的显著性检验的P<0.05，都通过了显著性检验，模型都具有统计学意义。 相比较第五个模型F 统计量的值最大。

回归系数的显著性检验，通过上表也能够看到第五个模型的系数都有意义，因此逐步回归的回归方程为：

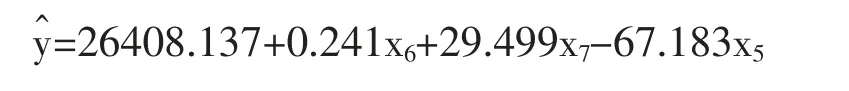
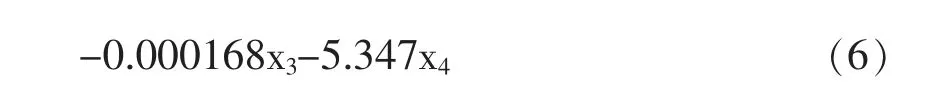
采用多元线性回归模型拟合误差检验的方法，并且结合赤峰市2010-2019年城市用水量的实际值，并通过回归方程，由此得到该指标的拟合值yˆ与城市实际用水量yi 的相对误差。 由表9 可知，该模型的最大相对误差为0.378%， 平均误差为0.241%，最小误差为0.058%。 预测结果表明该回归模型具有较好的预测精度，且采取了一种逐步回归式的分析。所构造的多元线性回归模型对于预测其价值具有十分重要的意义。

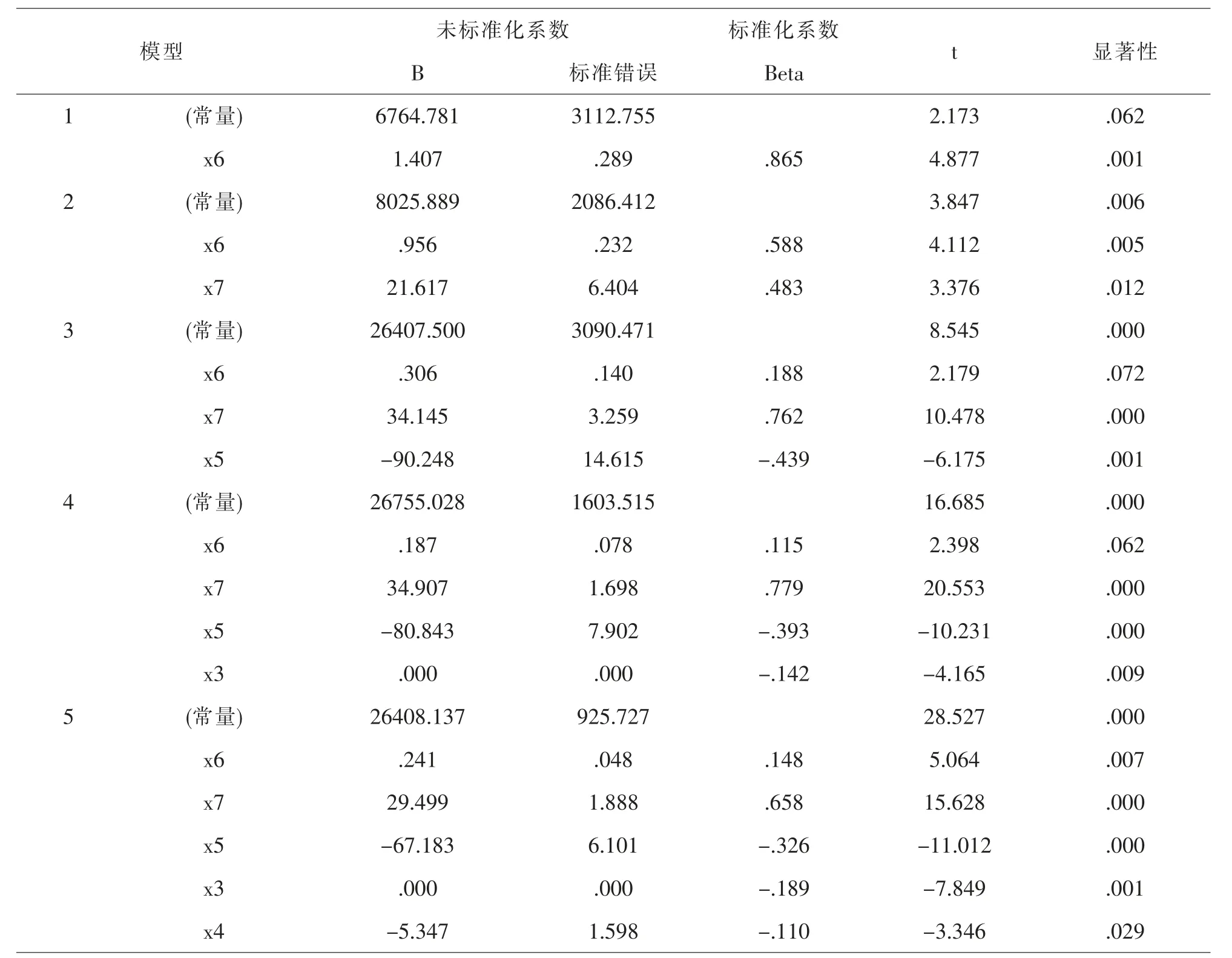
表8 系数a

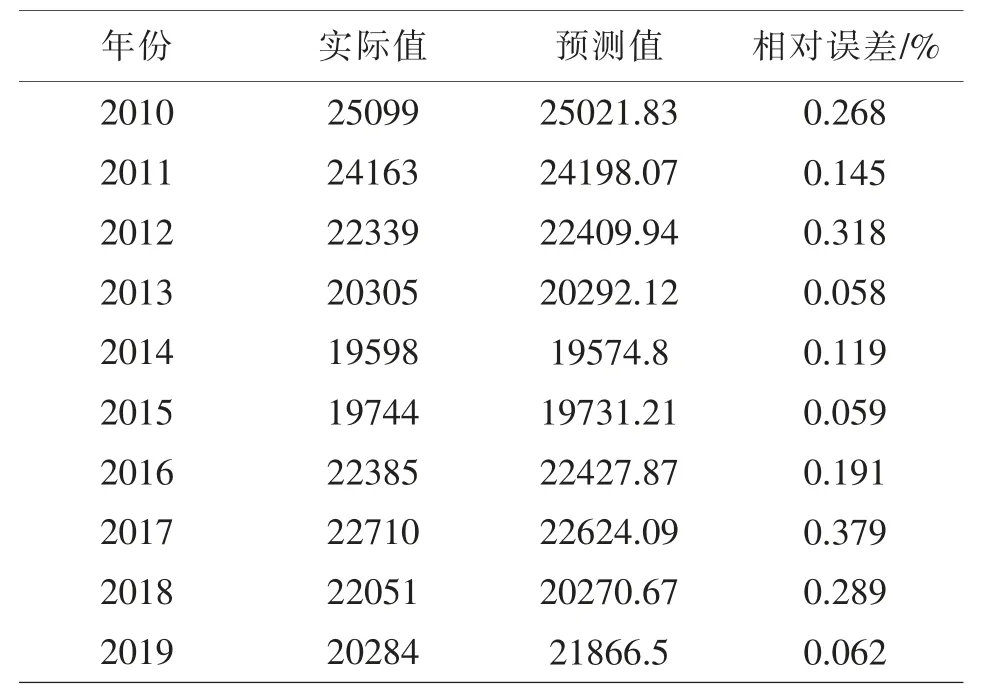
表9 多元线性回归方程的城市用水量拟合检验

3.3 赤峰市2021-2024年全年用水量预测

为了使用逐步回归方程预测2021年到2024年的年用水量，需要知道x4和x5两个变量在2021年到2024年的数据。 要获得变量x4和x5，2021-2024年的数据，需要分别建立变量x4和x5和时间的拟合方程。 将变量x4和x5分别绘制变量x4和x5时间曲线，以表1 中变量x4和x5的数据为纵轴。

图1 显示x4与时间t 近似为圆锥曲线，x5与时间t 近似为直线。 假定拟合方程式：

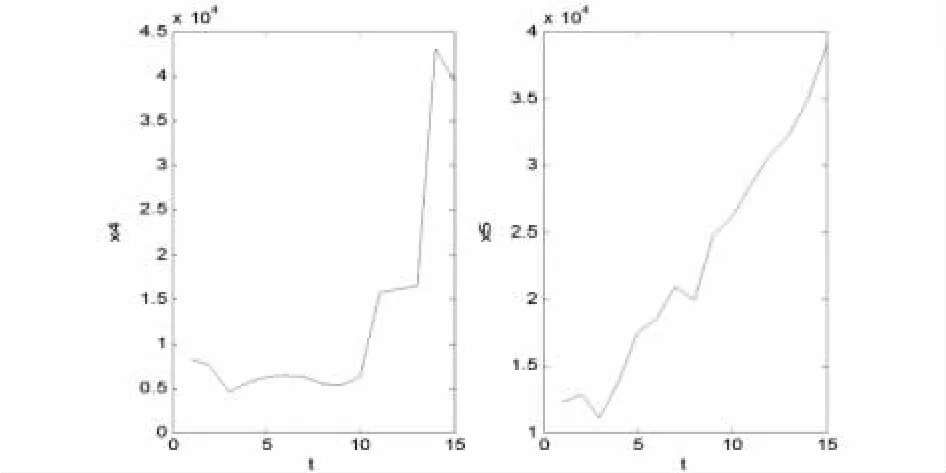
图1 变量x4 和x5 和时间的曲线图

其中a0，a1，a2，b，c 为待估参数。 将数据代入拟合方程， 运用非线性最小二乘法， 计算得a0=410，a1=-4563,a2=15430,b=1945.9,c=7316.7。

于是得拟合曲线方程为

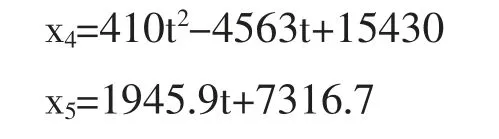
分别在t=16，t=17,t=18，t=19 计算出变量X4和X5的计算值(3)和(4)的预测值，然后用公式(1)计算出每年排水量Y，在预测年度计算结果中见表10。

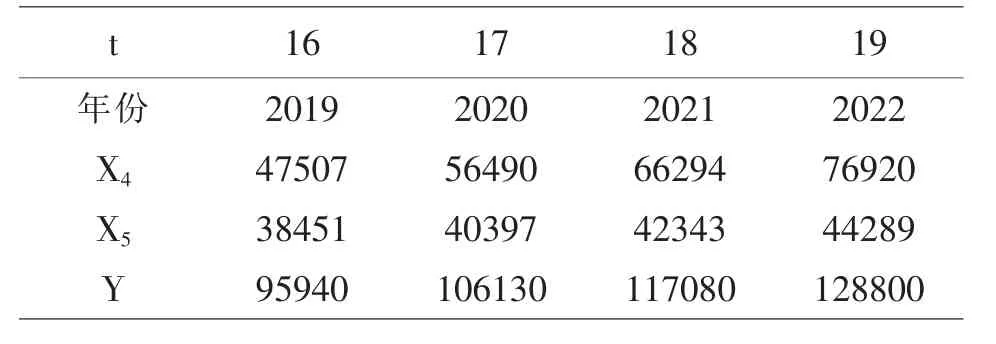
表10 2012-2024年的预测值

从表10 可以看出， 赤峰市2022-2024年预期年用水量为9.594 亿立方米、1.0613 亿立方米、1.11708 亿立方米和1.8888 亿立方米。

4 结论

城市用水量是由多种因素来决定的。运用多元线性回归的方法分析赤峰市的水资源供求状况，并采取了多元线性回归分析的原理和模型，对赤峰市的城市的用水量做出了预测。 利用自己所学spss软件基础知识，采取逐步回归分析方法，通过线性回归分析，建立回归方程，准确分析城市的用水量。最大误差为0.387%，最小误差为0.058%，平均误差为0.241%。 通过此次对赤峰市城市用水量的预测结果表明该模型具有良好的适用性，可以用于城市用水量的预测。 结果表明，该模型的相对预测误差最大值为0.378%，最小值为0.058%，平均误差为0.241%，表明该模型具有较高的精度，符合实际情况。 可以预测水的消耗量。 然后建立了一个多变量线性逐步回归模型，对赤峰市2021-2022年的用水量进行预测。 赤峰市的年用水量预计在2024年前达到12.88 亿立方米。 赤峰市应进一步优化水资源配置，防治缺水，以适应城市经济发展的需要。该方法建模过程简单，结果直观，精度高，大大减少了计算量，便于推广应用。