基于Winterstein/Jensen方法的深水海洋平台动力响应分析

徐 辉,范 强,柴俊凯,刘 圆

1.中国船级社海洋工程技术中心,天津 300457

2.中国船级社,北京 100007

1 概述

自国内第一个深水油气田（流花11-1油田）投产以来，我国已陆续建成了番禺30-1、番禺34-1、荔湾3-1等多座200 m级的深水导管架平台，近期刚建造完成的陆丰15-1导管架平台的水深高达280 m，而目前正在设计的流花11-1导管架平台的水深更是超过了300 m。随着“加大勘探开发，推动油气增储上产”国家策略的实施，我国海洋油气的开发不断向深远海挺进，海洋平台的规模与水深不断增大。相较于我国以往一般水深的平台，深水平台的环境荷载更为恶劣，其动力响应的影响也更为显著。

API[1]规范明确指出，当设计海况在平台固有频率附近包含显著的波能时，应对评估进行波浪动力响应分析。据统计，我国100 m级水深的导管架平台，其固有周期一般在3 s左右。国内通常采用均值法计算此类平台的动力放大系数（DAF）[2]，即根据不同随机波作用下的平台最大动基底剪力与最大静基底剪力之比的均值作为DAF。300 m级超水深导管架由于结构高度更高，整体重量更大，总体刚度更小，其固有周期会高达5 s左右，更接近设计海况中具有较高能量成分的波浪周期，所以动力响应更为显著。均值法的计算缺乏明确的规范依据和理论支撑，对300 m级超深水导管架的动力响应分析不具备可操作性。精准分析超深水平台的动力响应对平衡平台结构设计的可行性、建造成本的经济性、结构安全的可靠性具有重要的意义。

就位状态下的自升式平台和导管架平台均为通过桩基固定于海床的钢质平台，波浪荷载作用特点也相同，因此，计算自升式平台动力响应的方法也适用于导管架平台。SNAME[3]和ISO[4]规范给出了Drag-Inertia法、Weibull拟合法、Gumble拟合法和Winterstein法等四种推荐方法计算自升式平台的动力响应。CHEN Y N等[5]采用推荐方法研究了不同关键参数对深水自升式平台的结构响应的影响；LU Yan Jenny等[6]选取两座典型自升式平台对比研究了四种推荐方法得到动力响应结果，并认为Winterstein/Jensen方法是最有效的方法；Michael等[7]对比研究了18个样本平台的动力响应结果后认为当平台固有周期与设计海况谱峰周期之比大于0.6时，基于Winterstein/Jensen方法的动力响应分析结果最为可靠。因此，本文以南海某300 m级超深水导管架为例，给出了Winterstein/Jensen法分析超深水平台的动力响应的过程和结果，并与均值法的结果进行了对比，为今后的工程实践提供指导。

2 Winterstein/Jensen法

Winterstein/Jensen法是目前最为简便高效的波浪动力响应分析方法，通过对比平台动态响应和静态响应的最可能极值(MPM)得到平台的动力放大系数。对于高斯过程，可以直接计算响应过程的MPM。例如，MPM波高=1.86×有效波高。而对于一般的非线性、非高斯、有限带宽的过程，则需要采用近似方法来生成过程的概率密度函数。Winterstein[8]提出的拟合高斯过程的Hermite多项式法可以将非线性、非高斯过程转化为数学上可处理的概率密度函数。对峰度偏大的过程，需要采用Jensen修正方法对所拟合的过程进行修正[9]，自升式平台和超深水导管架的响应过程通常就是大峰度过程。

2.1 随机波浪的选择

采用Winterstein方法计算平台动力响应时，需同时模拟平台结构的静态和动态响应过程，所模拟时长应不小于3 h，以获取基底剪力和倾覆弯矩的最可能响应极值（MPME）。随机波浪的选取必须满足表1对均值、标准差、最大波峰高、偏度和峰度的要求，以确保输入的海况过程为高斯性。

表1 随机波浪的选取标准

随机波浪的波面根据波浪谱[10]（JOHNSWAP或PM谱），由一系列的规则波叠加而成，SNAME要求规则波的数目应大于200。

2.2 时间步长的设置

动力响应分析的时间步长应能准确反映较高的频率，SNAME规范要求时间步长应取Tz/20或Tn/20（Tn为平台的固有周期）二者之中的小者。ABS的研究发现[6]，时间步长可以取Tz/10或Tn/10二者之中的小者。考虑到动力响应分析的计算时间与计算精度之间的一个平衡，时间步长推荐采用介于上述两者之间的值。

2.3 响应的MPME计算

模拟时间内结构响应的MPME计算按下述步骤进行。

第一步，计算结构响应过程的统计参数：均值μ、标准差σ、偏度α3和峰度α4。

第二步，构建标准化的结构响应过程，Z=(R-μ)/σ，并利用该过程计算响应跨零周期的出现次数N。对于3 h的模拟时间，N可以假设为1 000。

第三步，利用第一步的特征值计算参数h3、h4、K。

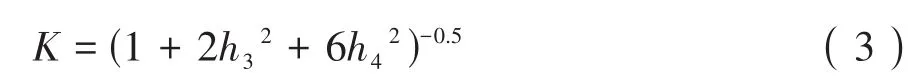
如果第一步计算得到的峰度α4≤5，则直接进入第四步；若α4＞5，则需要采用Jensen方法对参数h3、h4、K进行更新，更新方法如下。

（1）构建C1,C2,C3的三元非线性方程组；

（2）设置C1、C、C3的初始值，C1=σK(1-3h4),C2=σKh3，C3=σKh4。

（3）求解得到非线性方程组(4)，得到新的C1、C2、C3。

（4）更新参数h3、h4、K的值，K=(C1+3C3)/σ,h3=C2/(σK)，h4=C3/(σK)。

第四步，计算传递过程的最可能值U，该值代表零均值高斯过程。

式中：t为模拟时间，h。

第五步，计算转换成标准化变量的最大可能值ZMPM。

第六步，计算过程的响应最可能极值RMPME。

2.4 DAF的计算

根据SNAME推荐的Winterstein方法计算X、Y方向的结构静、动响应（基底剪力和倾覆力矩）的最可能的最大值（MPME）。MPME对应响应峰值概率密度函数的峰值，该值的超越概率约63%，即3 h的海况中1/1 000大峰值[11-13]。

结构响应的动力放大系数（DAF）为动响应和静响应的最可能的最大值的比值，公式如下：

式中：Fi表示X、Y方向的基底剪力和倾覆弯矩，d表示动态响应，s表示静态响应。

3 均值法

均值法是目前一般水深的平台所常用的一种DAF计算方法，随机选择30个种子，通过Airy波线性叠加生成随机波及基底剪力时程，并通过对比最大动基底剪力和最大静基底剪力得到动力放大系数DAF。在静力分析时，通过将DAF组合到波流荷载上，来简化考虑平台的动力放大效应。均值法计算DAF时一般有以下特点。

（1）所选择的波浪完全随机，不能保证模拟过程的高斯性。

（2）单个随机波的模拟时长一般在1 h以内。

（3）采用的是最大值，而非MPME计算DAF。

（4）DAF采用底剪力进行计算，未考虑倾覆弯矩的影响。

（5）取30个随机波的DAF均值作为平台的动力放大系数。

4 动力响应分析过程

本文利用Bentley公司的SACS软件的波浪动力响应分析模块计算海洋平台的结构动力响应，包含以下几个具体步骤。

（1）根据平台的结构图纸、设备布置图和重控报告等资料建立能体现平台真实状况的结构分析模型。

（2）根据设计海况的波浪参数进行桩基线性化，获得桩头的刚度矩阵。

（3）通过自由度凝聚法将结构质量、设备质量、海生物质量、充水质量和附加质量等集中到主结构节点，并通过模态分析得到平台的模态质量阵和阵型。

（4）采用100个随机种子模拟3 h的随机波面，从产生的波面中筛选出符合要求的随机种子。

（5）采用筛选出的随机种子进行动力响应时域分析，计算响应的MPME并计算DAF。

动力响应分析得到的DAF和MPME结果结合X、Y方向的一、二阶模态，通过计算可以得到合理分布的惯性荷载并用于平台整体静力分析[14]。

5 案例分析

5.1 平台概况和结构模型

本文以南海某超水深导管平台作为案例，分析其自存风暴海况下的动力响应，平台基本情况和分析模型如表2和图1所示。

表2 案例平台的基本情况

图1 动力响应分析的计算模型

5.2 桩基线性化

平台的桩基是利用经场址勘探的桩土曲线通过SACS程序的PSI模块进行模拟，在平台模态分析前需先根据设计波浪条件进行桩基线性化以确定对应海况条件下的桩头刚度，进而作为平台整体刚度的一部分。风暴工况下的桩基刚度如图2所示。

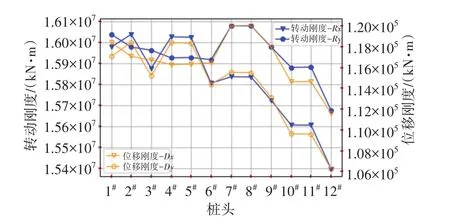
图2 桩基线性化后的桩头刚度

5.3 平台模态分析

将平台的340个主节点设置成质量凝聚点（222 000）以简化平台的自由度，形成了1 020×1 020的质量阵和刚度阵，并与桩基线性化后的桩头刚度阵形成了总刚度阵。本案例共计算了模态的前30阶阵型，前5阶的模态阵型特性如表3所示。

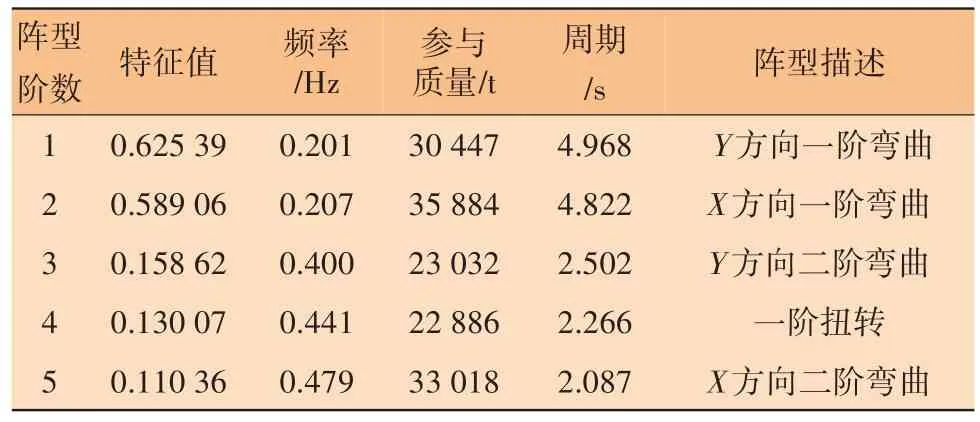
表3 前5阶模态特性

5.4 随机种子筛选

本案例采用Jonswap谱和随机选择的100个种子，模拟了100个持续时长11 000 s（3 h+200 s）的随机海浪，并从中筛选出了满足2.1节条件的种子（320）。种子（320）生成的随机波特性见表4，所产生的波面的均值和标准差见图3，均值和标准差在2 000 s时都达到收敛，模拟时长的前200 s为瞬态非稳定时程，因此在计算MPME时不予考虑。

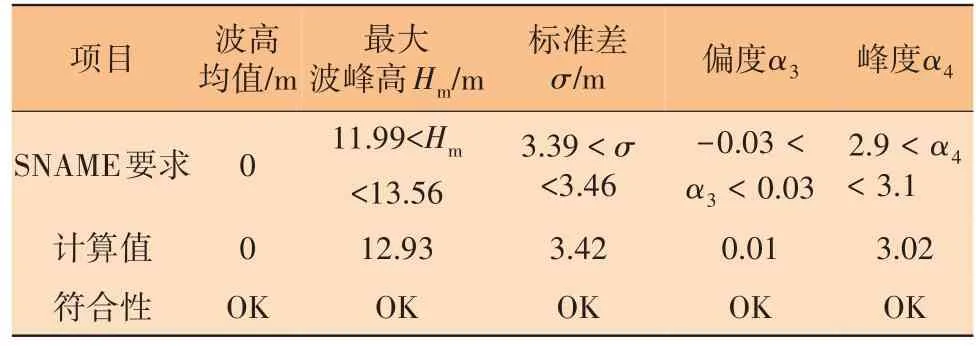
表4 种子320生成的随机波特性

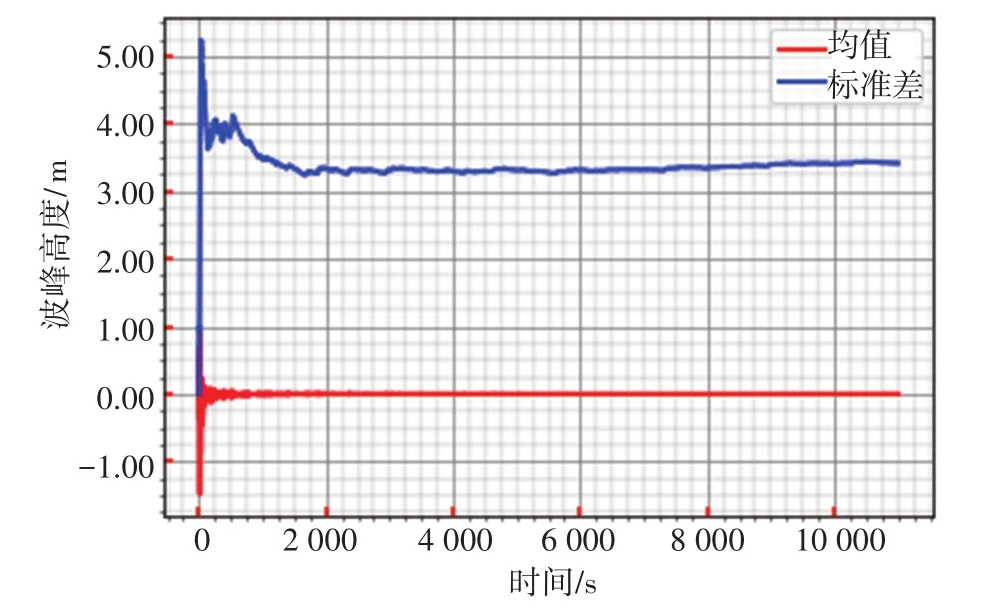
图3 种子（320）生成的随机波的统计特征

5.5 MPME及DAF计算

利用筛选的种子（320）进行动力响应分析，得到平台动态和静态的基底剪力和倾覆弯矩的时程响应。图4以45°方向为例给出了随机波浪响应的时间历程。不同方向的MPME和DAF的汇总结果见表5和表6。表6还给出了均值法计算的DAF结果。对比Winterstein法和均值法的DAF计算结果发现，均值法的DAF离散度较大，最大值为1.278，最小值为1.168，而Winterstein法以基底剪力确定的DAF都在1.250左右，以倾覆弯矩确定的DAF为1.200左右，各个方向的DAF结果一致性较好。用Winterstein法计算的DAF和MPME结果可以结合X、Y方向的一、二阶模态计算得到合理分布的平台惯性荷载，具有更强的合理性和实用性。

图4 基底剪力和倾覆弯矩的响应时程（45°方向）

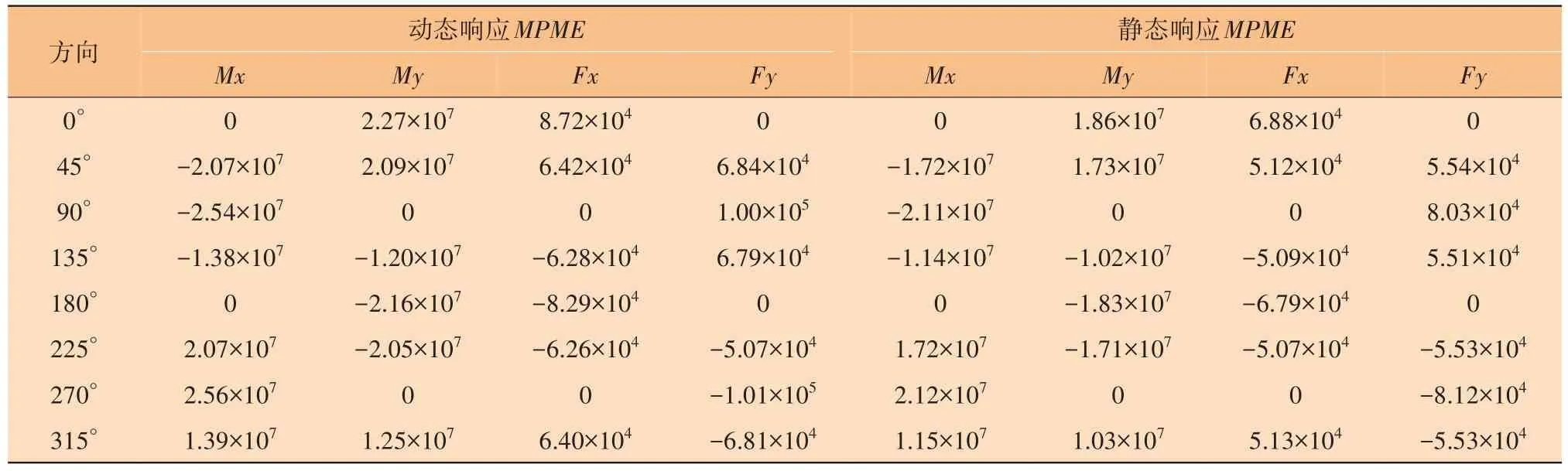
表5 不同方向MPME汇总

表6 Winterstein法及与均值法的DAF对比

均值法与Winterstein法所得结果的差异有以下几个原因。

（1）均值法模拟的时长较短，通常为1 h，最可能的极值有可能尚未出现。

（2）均值法未排除模拟时长的前200 s的不稳定过程。

（3）随机种子未经过筛选，所生成的随机波不完全满足高斯性。

（4）只考虑基底剪力的响应而忽略了倾覆弯矩响应对DAF的影响。

6 结束语

针对超深水海洋平台动力响应显著的现实，本文结合实际案例平台给出了基于Winterstein法的动力响应分析过程，计算了平台响应的MPME和动力放大系数DAF。通过对比Winterstein法与以往一般水深海洋平台常用的均值法，进而得到以下结论。

（1）Winterstein法是SNAME规范中推荐的DAF计算方法，具有明确的理论依据和规范支撑，均值法较多应用于一般水深的平台，但其缺乏明确的规范和理论支持。

（2）Winterstein法通过随机波浪种子的筛选，所模拟的波浪具有足够的高斯型，而均值法所模拟的波浪是完全随机，不一定具备高斯性，计算结果会有一定的偶然性。

（3）Winterstein法计算的各个方向的DAF值一致性好，且同时考虑了基底剪力和倾覆弯矩的影响，而均值法的结果离散度较大，仅仅考虑了基底剪力的影响，也没有排除模拟时长中首部不稳定过程的影响。

（4）Winterstein法计算的MPME和DAF可以结合平台X、Y方向的一、二阶模态，计算得到作用于平台质量凝聚点上的惯性荷载。

综上，Winterstein法能更为科学合理地计算平台的动力响应，本文推荐采用Winterstein法计算超深水海洋平台的动力响应分析；对于一般水深的平台，最好也采用Winterstein法；如果采用均值法，应进行波浪筛选以选取具有足够高斯性的随机波浪进行动力放大系数的计算。