百万吨级CO2捕集烟气集成处理塔流场模拟及优化
韩 冰,李清方,刘海丽,于惠娟,张舒漫,王 辉
1.中石化石油工程设计有限公司,山东东营 257000
2.山东莱克工程设计有限公司,山东东营 257000
CO2捕集利用与封存(Carbon Capture Utilization and Storage,CCUS)技术是目前最有效的去碳技术[1-3],其中CO2捕集是最核心的工艺流程。胜利发电厂100×104t/a CO2捕集与利用工程是国内规模最大的电厂碳捕集利用(CCU)项目,目前项目处于设计阶段[3-4]。为精简工艺流程,降低工程建设成本,经过研究和论证,拟将CO2捕集工艺流程设备合并为一个烟气集成处理塔(以下简称IPT或塔)[5-6]。IPT高度约65 m,容积1.9×104m³,为特大型容器,无规则形状,内部填料段的复杂程度远高于常规塔器[7-8]。由于IPT为新研发设备,因而在设计研发阶段需使用有限元软件对此问题进行研究[9-10],并对IPT进行深入的优化和改进。
1 基础理论和模型建立
1.1 立题背景
由于IPT是CCUS技术中首次被提出的概念,需在研发和设计阶段进行充分验证,对IPT的结构进行充分试错,才能保证IPT在实际应用中达到预期效果。从提出IPT的概念到施工图的定版过程中,会对IPT进行可行性研究和诸多优化改进。优化目标是使烟气在所有填料段内均可均匀分布,并保证尽可能小的全塔压降,本质上这是一个研究气体在大型不规则设备中固流耦合状态的优化问题。
在当前的工程技术下,研究此问题的方式主要有以下两种:
(1)建造实验室模型或中试模型。
(2)使用有限元软件对IPT虚拟模型进行流体仿真模拟。
本文采用上述第2种方式进行深入探讨。
1.2 无量纲数y+
为了更精确地描述流动状态,需要对湍流边界层分层并分别描述,同时反映边界层的相对位置,为此引入一个无量纲数y+。一般将y+描述为:

式中:μτ为壁面附近流体的剪切速度,m/s;y为计算节点离壁面的距离,m;ϑ为运动黏度,m2/s。
y+可以近似理解为y处的雷诺数,同时也反映了黏性影响随y变化的特征。y+的引入意味着将湍流边界层分层,y+较小说明流体贴近壁面,在壁面上流体脉动速度为零,湍流应力很小,此时黏性对流动状态的影响占主导地位;反之则惯性力占主导地位。y+是湍流模型选择的重要依据之一。
1.3 湍流模型选择
一般常用的湍流模型有:固定湍流黏度、混合长度、K-ε、K-ω、切应力传输(Shear Stress Transfer,以下简称SST模型)、SA(Spalart-Allmaras)、LES大涡。固定湍流黏度和混合长度一般称为零方程模型,即直接使用平均流动物理量来模化涡黏性系数,而不引入任何湍流量。同样的,SA模型为所谓的单方程模型,即引入了一个湍流量;K-ε和K-ω归为所谓的二方程模型,即引入了两个湍流量。K-ε为求解湍流动能(Turbulent Kinetic Energy,以下简称TKE)湍流标量K和TKE耗散率ε的输运方程;K-ω则为求解K和单位TKE耗散率ω的输运方程。切应力传输SST相当于对K-ε和K-ω的改进。
烟气在入口管道中的设计流速为12 m/s,空塔气速设计范围为1~2 m/s,很显然本案例为高湍流稳态模型,所以可以首先排除层流模型、SA模型(此模型在高雷诺数下的性能不理想)、LES大涡模型(用于计算瞬态流场)。固定湍流黏度模型和混合长度模型由于只能描述一个湍流量,本案例也均不选用。对其余模型的选择理由如下:
1.3.1K-ε模型
根据经验,此模型对于自由流动、带旋转的流动以及带有强烈反向压力梯度且y+<11的流动,计算性能很差。K-ε模型将每个流体节点处的流动湍流黏度μt描述如下:

式中:μt为此模型下假设的流体在计算节点处的流动湍流黏度,即用来描述湍流涡旋扩散而使流体宏观上产生附加黏度行为的量,因此μt为模化量,无量纲;ρ为流体密度,g/mm3;Cμ为常数,一般取0.09,k为湍流动能TKE,J;ε为TKE的耗散率,%。
因为k和ε的耦合传输方程在三维流域中的所有流体节点上都得以解算,所以湍流黏度在整个流体域中都是变化的。
1.3.2K-ω模型
与K-ε模型的描述相似,K-ω模型将每个流体节点处的流动湍流黏度μt描述如下:

式中:μt为模化量;ρ为流体密度,kg/m3;k为TKE,J;ω为TKE的特定耗散率,%。
与K-ε模型一样,由于k和ω的耦合传输方程在三维流域中的所有流体节点上都得以解算,所以湍流黏度在整个流体域中都是变化的。但此模型对入口自由流体湍流属性过于敏感。
1.3.3 SST模型
SST模型结合了K-ε和K-ω模型。在y+较大时,SST模型的行为和K-ε模型相同;在y+较小时,SST模型的行为和K-ω模型相同。SST模型还可以很好地计算自由流动和带有强烈反向压力梯度(如存在较多流动死区或阻力带)的流动情况。
综合考虑,选择SST模型作为IPT的流场计算最为合适。需要说明的是,所有的两方程模型均可提供平均流量上湍流效应的精准计算,但需要一个较为精细的3D流网格,由于在IPT这样的超大模型上应用会产生巨大的计算量,所以在进行优化分析时,每次只操作单个塔填料段(或功能区),这样网格收敛速度较快,问题标的和分析精度都更为精准。
1.4 问题简化
在有限元分析的前处理中,需要首先明确以下几点:
(1)选取烟气的节点速度(以下简称气速)作为不均匀度的统计值。
(2)使用气速样本中的标准差来表征不均匀度,标准差越小,不均匀度越小,即分布越均匀。
(3)烟气到达每层填料段时如果分布均匀,由于填料段自带再分布器,可近似地认定为在填料段内也分布均匀,即填料段的存在并不影响分布趋势。所以填料段内结构无需建模,只分析空塔即可反映实际情况。
(4)不考虑降液对烟气分布造成的影响,但烟气分布器的结构不能影响降液的收集。
(5)不考虑温度场,且为光滑壁面(有摩擦且为恒定值)。
(6)不考虑接管开孔,但考虑进出口的气速突变而保留进出口烟道。
(7)通过进出口总压力值计算空塔压降,使用烟气分布器前后的压降之差即为烟气分布器自身的压降。
(8)气体成分并不影响模拟趋势,所以模型使用空气替代烟气作为计算介质。
1.5 模型建立
将塔器的内部腔体1∶1建模,作为有限元计算的流体域,烟气的进口和出口各建立长度为10 m的烟气管道,折合烟气进口流量为252 m³/s。使用4节点四面体网格划分。
在IPT的每个拐角处设置扰流板,建模中用圆角代替,此举是为了减小拐角突变带来的干扰,使之后添加烟气分布器的效果更加纯粹。此时为初始模型,标记为模型A,如图1所示。

图1 IPT模型A轴测示意
2 初步解算结果及模型改进
2.1 初步解算结果
利用有限元模型A求解得到塔内气速分布,如图2所示。

图2 模型A塔内气速分布/(m·s-1)
从图2(a)可以看出:气速在各填料段内的分布非常不均匀,预处理段和处理段由于扰流板的强制换向,已经出现了左右速度分区的现象。
从图2(b)可以看出:存在两个大的涡流,分别位于处理段和干燥段。需要说明的是,干燥段不存在传质操作,所以存在的涡流并不影响工艺性能,只是涡流的空洞侵占了部分塔内空间,会造成效率下降。因此对此涡流可以不消除,但要尽量缩小涡流范围或填充空洞。
2.2 解算结果
针对上述问题,根据图2的气速分布特点对模型进行改进,改进后的模型标记为模型B,如图3所示。
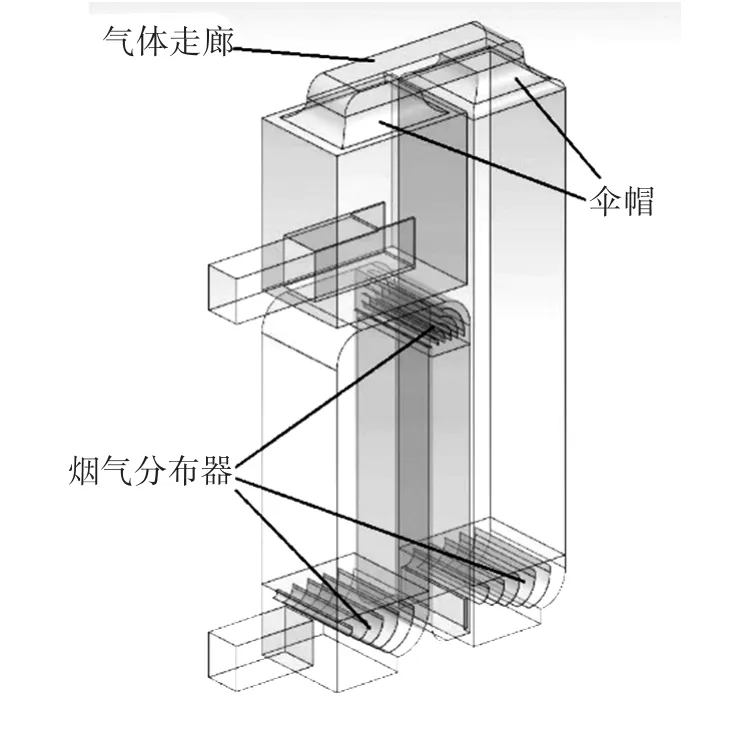
图3 模型B轴测示意
具体改进措施如下:
(1)使用烟气分布器对恶化较为严重的流场前端进行分割和导向,以削弱大流道带来的湍流程度,并降低扰流板强制换向带来的反弹效果。
(2)烟气从处理段到干燥段由塔器顶部过渡完成,在此过程中气速方向是完全相反的。所以塔器顶部不采用烟气分布器,而改为更为有效的收集伞帽和再分布伞帽,以对烟气平稳“调头”。
(3)限于塔器周边的管道和建筑遮挡,出口烟道无法改成理想的两侧出口。将烟道插入塔内,并斜上45°开口,用于和塔顶来气形成垂直的气流路径,减少涡流。
利用有限元对模型B求解得到塔内气速分布,如图4所示。
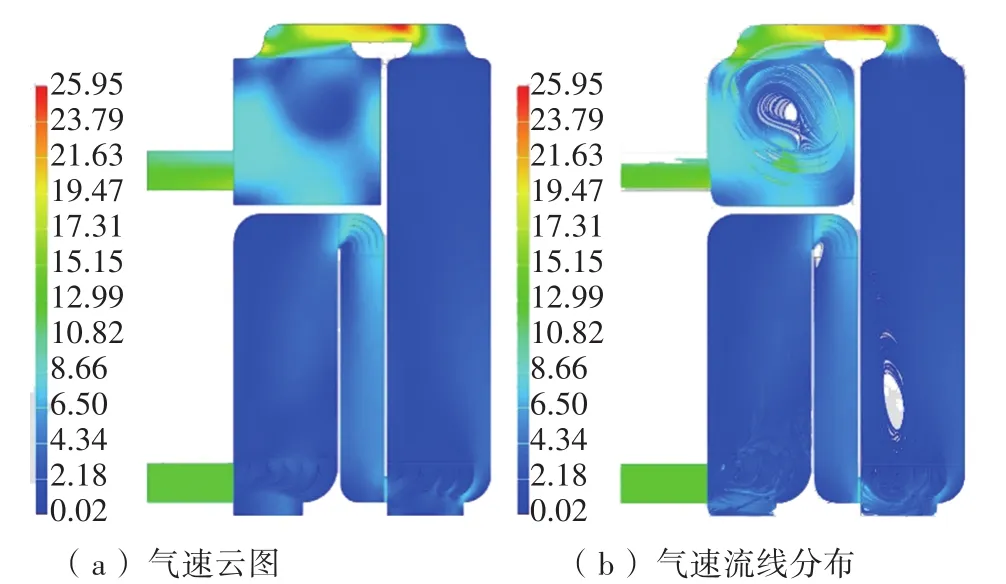
图4 模型B塔内气速分布/(m·s-1)
从图4可以看出,模型B具有如下特点。
(1)预处理段的烟气已经均匀分布,即已经优化完毕。
(2)干燥段的涡流依然存在,但要小很多,且中间空洞减少较多,对效率的影响已可以接受。之前已经论证过此处的涡流可以存在,较为理想的解决方案是填充。所以判定干燥段也已优化完毕。
(3)由于外部空间原因,塔顶两个伞帽之间的气体走廊设计得较为狭窄,造成此处的气速较高,为25.95 m/s,但不影响烟气在填料段的分布性能。
(4)处理段的涡流依然存在,位置向左下方移动,且变得更为狭长,后面有多个弧形空洞出现,并呈现出剥离趋势。说明之前的大涡流在这里已经演变为涡街。涡街的存在可能会引起填料层振动,此塔的大跨度填料层对振动又是较为敏感的,所以涡街必须消除。
为消除涡街,需要改进烟气分布器。理论上的改进方案有二。
(1)增加分布器导流板数量,可将烟气分割得更为细化,但对消除涡街作用较小,可能会将原涡街分割成更小的涡街。导流板数量越多,分布器的气阻也会越大。
(2)延长分布器导流板的长度,可增加烟气的稳定路径。延长方向可分为正向(即延长方向与烟气流动方向相同)和反向。反向延长可使烟气从初始状态就被分割,并减少进入分布器前的乱流,但此结构会影响降液的收集。
综上所述,将烟气分布器的导流板正向延长2 m。考虑到其他部分均已优化完毕,将整体模型参与计算只会增加无效计算量,延长后更为细长的烟气分布器会破坏整体网格质量,故将处理段分割出来单独进行优化。将预处理段和处理段之间的烟道状态作为边界条件,建立有限元模型,标记为模型C,将模型C解出速度流线图,如图5所示。
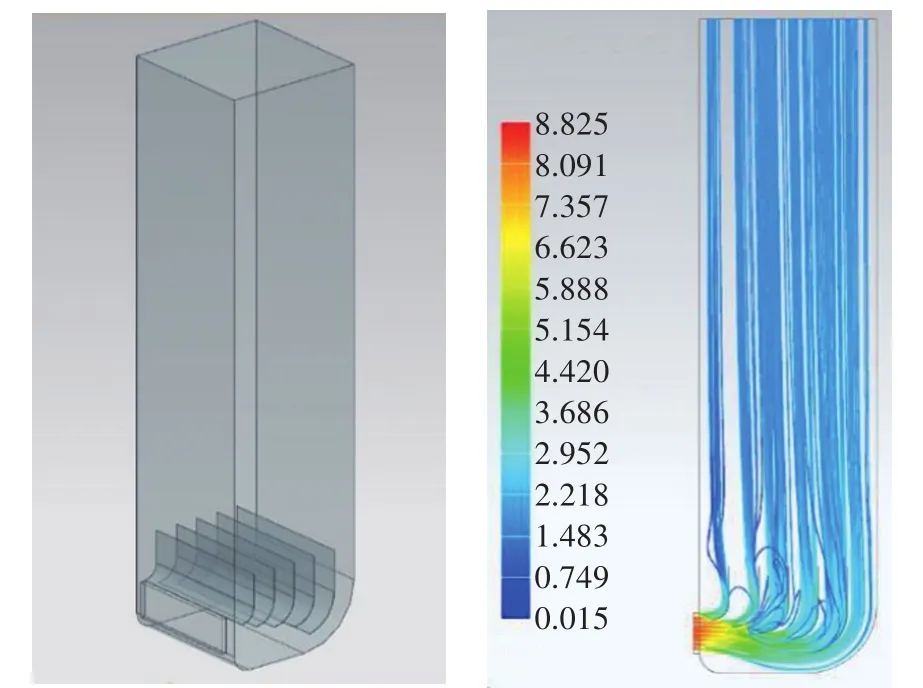
图5 模型C及其速度流线/(m·s-1)
从图5可以看出,改进后的烟气分布器已经完全消除了涡街,且可以很好地将烟气分布均匀。至此,IPT全部功能区均已完成优化。
云图和流线图可以很直观地看出趋势和判定效果,但精确的数值统计需要对云图进行采样。根据采集的数据,进行定量分析和对比。
3 数据分析及结论
3.1 数据采集和分析
在模型A和模型B中相同的位置进行采样,采样点(即采样面上所有点)分别位于预处理段、处理段、干燥段。在模型C中间截面处取样,用于和模型A及模型B的处理段样本进行对比。采样位置如图6所示。

图6 采样位置示意
气速单位按mm/s整理出采样点的标准差。因模型A~C均含有处理段,图7将其全部列出。

图7 各模型处理段样本气速分布
从图7可以直观看出离散点在模型A~C中的分布愈趋于集中。经统计,模型A处理段标准差为1 812,模型B处理段标准差为1 158,模型C处理段标准差为792。
限于篇幅,其他填料段的过程数据不再列举。将所有填料段的最终数据整理至表1。
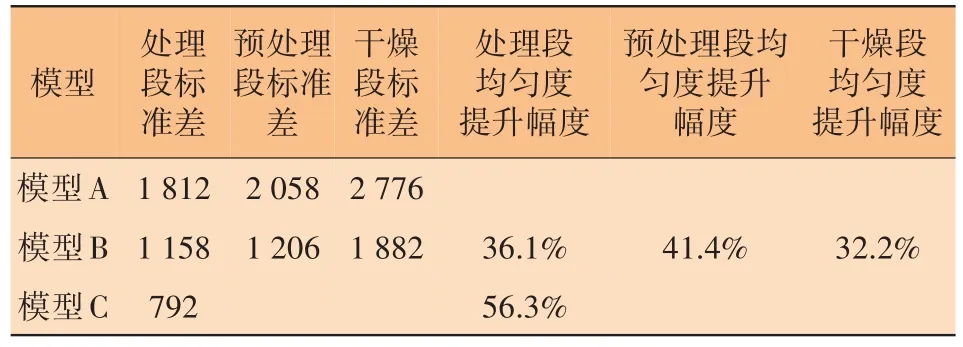
表1 各模型填料段标准差和烟气分布均匀度提升幅度
增加烟气分布器后,全塔压降由245 Pa增至852 Pa,增大了607 Pa,工艺上对IPT整体压降的要求是控制在8 kPa以内,烟气分布器带来的压降占比仅为7.6%。
3.2 结论
由表1可知,优化后的烟气分布均匀度相比初始模型,处理段提升了56.3%,预处理段提升了41.4%,干燥段提升了32.2%。每个填料段的分布均匀度提升幅度是相当可观的,说明优化方向正确,优化效果显著。在添加烟气分布器后,压降仅增加了7.6%,对塔器引风机造成的压头损耗比较小,说明优化后的烟气分布器工艺性能优良。
4 结束语
本文所述烟气分布器结构精简、可靠,建造成本低,性价比高。此结构的引入为方形塔器气体分布器的设计提供了新的设计思路,为IPT的整体设计指出了正确方向。同时,使用有限元分析验证,相比采用建造实验室实体模型或中试模型等传统方式,可以显著降低新设备在研发过程中的试错成本,大幅提高设计效率,近年来被广泛应用于各类工程案例中,产生了巨大的经济效益。由于无需建造实体验证模型,所以降低了研发设计过程中的碳排放,做到了“过程减排”和“二次减排”。

