水平主导地震作用下高桩码头抗震设计分析

刘树明，李伟仪，朱 峰

（中交第四航务工程勘察设计院有限公司，广东广州 510230）

引言

Pushover分析法与传统的抗震静力方法区别主要在于它考虑了结构的弹塑性性能并将设计反应谱引入计算过程中，相比于弹性分析方法，更能反映结构的弹塑性性能[2]，又比弹塑性动力时程分析方法简单，具有较强的实用型。

Pushover分析法的核心是能力谱法。能力谱法最早由Freeman等[3]在1975年提出，该方法将结构的Pushover曲线转换为能力谱，将反应谱转化为需求谱，并通过不断改变结构的位移最终使结构的能力和需求相等来确定结构的性能点，性能点对应的位移称为目标位移。本文基于Pushover分析法，利用sap2000计算软件，针对某工程高桩码头抗震稳定性进行了分析。

1 项目概况

Pushover分析法主要适用于单自由度系统。大部分梁板式和无梁板式高桩码头，码头的大部分质量集中于码头面上，可直接等效为单自由度体系。图1为某无梁板式高桩码头装载平台断面，排架横向间距为7.5 m，平面尺寸为42×35 m，桩基采用钢管桩，管径为1.2 m。面板采用等级为C35/C45混凝土，钢筋采用B500BWR，钢管桩材料为S420MH。

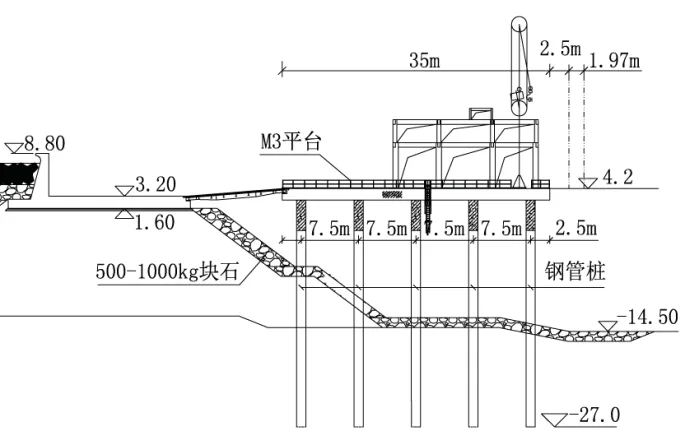
图1 装载平台剖面示意

2 地震工况

2.1 抗震设计标准

抗震设计标准是开展结构抗震设计的重要参考依据，基于Hamdache和Retief等人的研究成果[4]，得到项目位置处重现期475年的地震震级为6.34级，地表处PGA设计值0.15g；重现期4975年的地震震级为6.72级，地表处PGA设计值0.32g。

2.2 地震荷载计算

根据欧洲标准EN1998-1:2004相关定义，地震作用的水平分量设计反应谱Sd(T)可以表达为：

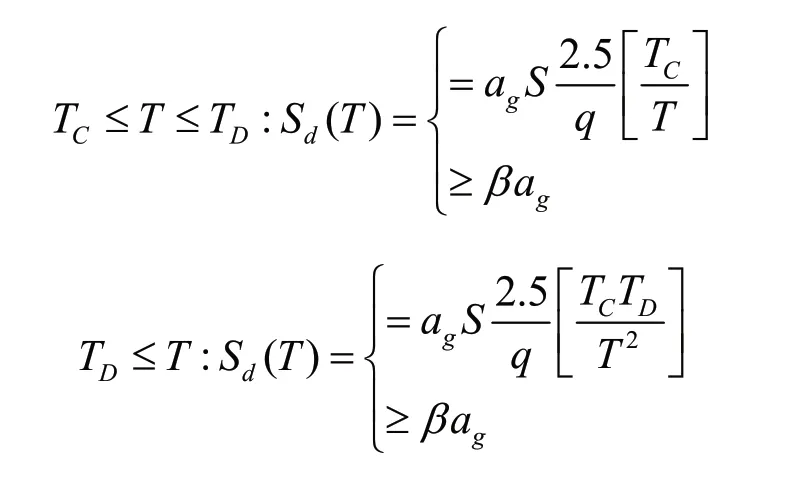
式中：ag为A类场地的设计地震加速度；TB为恒定频谱加速度的下限周期；TC为恒定频谱加速度的上限周期；TD为定义恒定位移响应范围的起始周期；S为土体系数；Sd为设计频谱；q为性能系数；β是水平设计频谱的下限系数。综上得到5 %阻尼效应下面板结构设计响应谱如图2、图3所示。

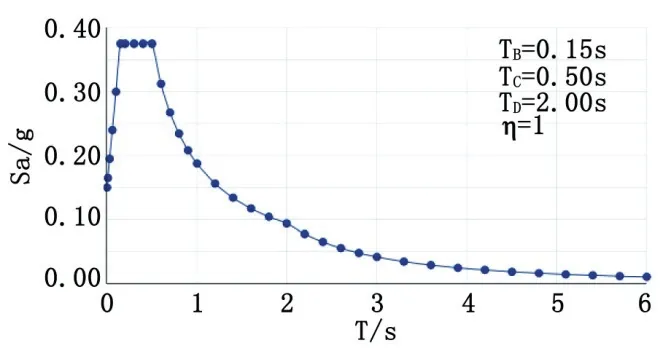
图2 Pushover分析水平向弹性反应谱（OBE）

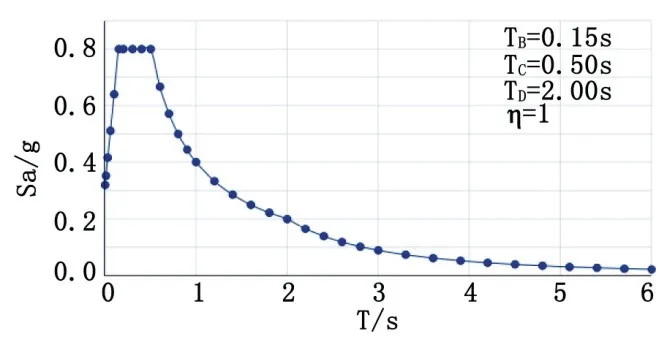
图3 Pushover分析水平向弹性反应谱（SSE）

3 Pushover分析

3.1 材料预期特性

预期材料特性用于确定桩塑性铰承载力以及评估平台整体承载力，Pushover分析中材料预期强度值取值为fye=1.1fy。其中为混凝土28天无侧限抗压强度，fy为钢结构或钢筋的屈服强度。有限元模型中的材料属性设定如表1和表2所示。

表1 混凝土材料特性

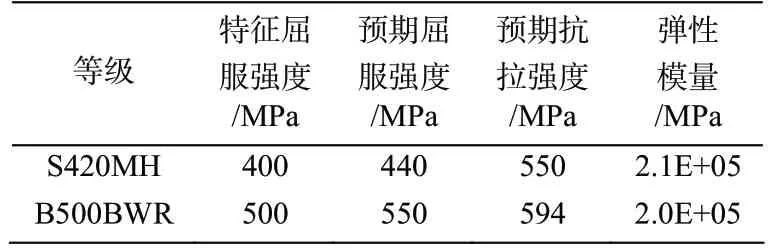
表2 钢材材料特性

3.2 截面属性

根据工程设计中，桩基本身的特性（是否填有桩芯混凝土）以及桩基与上部结构的连接情况，可以将桩基的截面特性简化为三个典型断面，分别为混凝土嵌入段、钢管桩芯混凝土段以及普通钢管桩段。结构力学模式如图4所示。

2013年尚水信息成功研制了国际首例同步测量超大范围流场系统、PLIF浓度测量系统、三维模拟决策分析平台等创新产品。公司以多年积累的数字实验室经验为技术依托，更将水利水运行业数字实验室中的尖端科技引入至水利水运原型测报与分析领域当中，为山洪灾害预警监测、水资源监控及管理、中小河流监控及管理、智慧水务等方面提供全面解决方案，完成了“智慧城市——城市内涝监测系统”“湘江航道航标遥测遥控通讯平台”“环保公益课题——水文监测项目”等多个项目。

图4 结构嵌入段和桩芯混凝土段力学模式

上层结构和桩之间的连接不应视为完全刚性。桩顶有效顶面与面板底部距离Lsp考虑嵌入条件下的应变协调。桩顶有效顶面与上部结构的重心之间的构件视为刚性链接。根据本项目的实际设计情况，以及POLB WDC[5]中的相关建议，Lsp的数值取为0.36 m。

不同桩截面的弯矩曲率计算均假定满足平截面变形规定，通过将断面进行离散的方式（如图5所示）分别计算不同P-M组合条件下每个子区间的应力应变状态，从而累积得到整个截面在不同正压力下的弯矩-曲率曲线。

图5 桩截面弯矩-曲率计算示意

通过对不同类型截面进行计算，得到三个典型截面不同正压力下所对应的弯矩-曲率关系如图6。

图6 桩基不同截面特性弯矩-曲率

3.3 塑性铰分布

地震过程中，当桩中部分区段内的钢筋达到屈服强度，但截面弯矩仍小于极限值时，此处形成一个塑性铰。在有限元模拟过程中，屈服和后屈服行为可以用离散铰模拟，每个铰点代表一个潜在的塑性区域，并可以自定P-M2-M3耦合弯矩曲率力学曲线，考虑塑性铰处轴向力和双轴弯矩相互作用。桩体的塑性铰主要分布在可能出现较大弯矩的位置，以及发生截面属性突变的位置，因此计算中对每根桩设置6个塑性铰，分别位于桩顶嵌入平台内Lsp位置处、桩与平台面板下表面交接处、桩芯混凝土底部，以及泥面以下每隔约2D深度设置一个（共计设置3个点）塑性铰如图7所示。

图7 塑性铰分布示意

3.4 桩土接触面

土壤对桩体的侧向约束效应采用p-y弹簧进行模拟，沿土壤深度设置水平弹簧，API-2GEO[6]对土弹簧的基本定义如下所示：

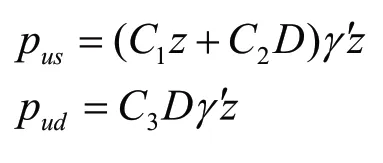
其中：p为土弹簧抵抗刚度，下标us表示土层上表面，ud表示土层下表面；z为图层深度；D为桩直径；C1～C3为系数。

3.5 结构Pushover荷载-位移曲线

针对上一节中所定义的带塑性铰结构模型进行加载，加载方式为对码头上部结构按照X+0.3Y方向（X轴和Y轴分别平行码头前沿线方向和垂直码头前沿线方向）逐步施加水平推力，直至模型达到破坏临界状态，可以获得图8所示的荷载位移曲线。

图8 承载平台pushover曲线

从图8中可以看到：随着荷载的不断增加，结构的位移先后经历线性增长和非线性增长，直至破坏，与实际结构受力变形规律相符。根据欧洲标准EN1993，混凝土、钢筋以及钢管桩的应变需分别满足OBE工况下“最小破坏”和SSE工况“可控可修复破坏”的标准[7]，不同构件的应变极限如表3所示。

表3 OBE工况应变极限[8]

由此可以确定在满足结构可靠性前提下，OBE工况允许结构位移为0.301 m，SSE工况允许结构位移为0.550 m。

3.6 结构性能点

有了承载平台Pushover曲线后，结构性能点的寻找是一个不断迭代的过程[8-9]。在结构Pushover曲线与某一阻尼下的需求谱求得交点后，可以通过Pushover曲线查询该点的阻尼与需求谱的阻尼是否一致，如不一致则需要更新需求谱求取新的交点[10]。图9和图10展示了这一迭代过程。

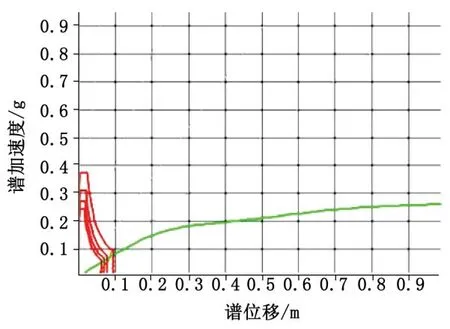
图9 承载平台性能点(OBE)

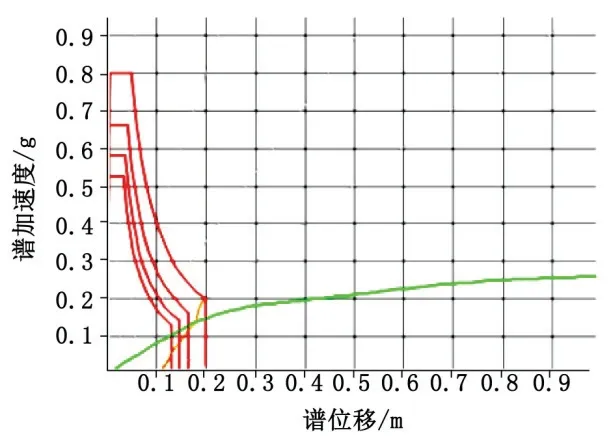
图10 承载平台性能点(SSE)

基于上述步骤，通过数次迭代后即可获得本文结构形式在指定地震工况下的需求位移以及对应的阻尼比。计算结果和限制位移之间的比对如表4所示。从结果中可以看到：随着PGA的放大，结构位移响应幅值的不断增加，对应的结构阻尼也有所增加，但是总体而言均在对应的安全限值以内。

表4 性能点计算结果

为了进一步验证Pushover计算结果的有效性，本文基于上述结构模型，采用人工合成地震波开展了非线性时间历程分析，计算结果如表5所示。从计算结果可以看到：Pushover方法计算结果相比时间历程法内力响应偏小，可能是由于人工合成地震波在局部位置大于目标谱以及Pushover方法过度考虑了阻尼的作用导致，但是计算结果在大体上两者一致，证明Pushover方法在一定程度上可以满足工程实际应用。

表5 结果对比分析

4 结语

本文采用有限元计算软件，基于Pushover非线性静力方法，开展了某无梁板式高桩码头抗震设计计算，计算结果表明：

1）Pushover分析法基于反应谱理论和结构自身的非线性变形特性构建出较为完整的抗震设计理论体系，可以较为全面的获得结构弹塑性变形曲线和桩基承载力，为校核设计结构的抗震稳定性提供了重要的理论依据。

2）Pushover分析法与非线性时间历程法相比，计算结果整体上保持相一致，但由于无法考虑结构的动态扭转效应以及阻尼的预估较为粗略，导致结构整体的分析结果略微偏小。

基于pushover分析，针对特定工程案例开展设计计算，并运用国内水运工程项目设计中，有利于在关注结构安全的同时定量评估地震引起的结构损伤，可以指导结构的震后工程修复与加固。