自动化机器人轨迹跟踪与路径规划技术研究
杨金铎,王林波,曾 惜,王 冕,周 慧
(1.贵州电网有限责任公司贵阳供电局,贵州 贵阳 550001;2.广州中科云图智能科技有限公司,广东 广州 510180)
0 引言
进入21世纪以来,人工智能技术已成为世界经济社会发展的重点,在全球经济发展中发挥着重要作用。作为人工智能技术发展项目的重要组成部分,机器人领域的研究成果不断涌现。随着自动化机器人广泛进入社会生活的各个方面,如何提升自动化机器人的性能无疑成为科学研究的重点。当前阶段,自动化机器人在开展具体作业时受到移动方向的限制。由于自动化机器人的移动方向并不是任意的,因而涉及其轨迹跟踪与路径规划研究时,需要综合固定移动方向限制带来的约束影响,探索对自动化机器人进行有效控制的技术[1]。在自动机器人路径规划研究中,基本思想是根据最小能耗、最短路径、最短时间等一个或多个优化指标,规划一条安全的最优路径,以避开当前位置与目标位置之间的障碍物[2]。文献[3]通过确定运动场景里的追踪目标、机器人位置以及障碍物信息进行局部或全局路径划分。文献[4]指出了多种全局路径规划算法,主要包括栅格法、拓扑法以及可视图法。在机器人研究领域,轨迹跟踪是一个重要的运动控制问题。机器人轨道跟踪是指在惯性坐标系中,机器人在控制器的作用下,从起始位置出发,沿给定的、相对于时间的轨迹运动[5]。文献[6]根据建模过程中选择控制输入的不同,结合运动学模型与动力学模型,实现了自动化机器人的轨迹跟踪。文献[7]指出了多种轨迹跟踪控制算法,主要包括神经网络控制、滑膜控制以及自适应控制算法。
概而言之,由于传统自动化机器人运动控制算法难以综合考虑路径安全性、路径规划长度、以及移动转弯角度等系列问题,不能很好地进行路径最优规划以及有效轨迹跟踪。本文通过更新并改进技术算法,为自动化机器人规划出平滑且安全的路径,具有应用价值。
1 轨迹跟踪与路径规划实现算法
1.1 基于A*算法的全局路径规划
传统A*算法在进行自动机器人全局路径规划时,由于冗余点较多、移动转折角度过大以及转折次数过多等问题,使得机器人无法探索最优路径。为此,本文提出了一种基于A*算法的改进算法。首先,通过对预定的轨迹路径进行处理,将全局路径分为起点、转折点和重点三部分,以消除机器人运动路径中所有冗余点造成的不利影响。然后,在保证机器人与障碍物之间安全距离的同时,完成机器人运动的路径长度寻优,并有效减少运动过程中的路线调整次数,从而实现全局路径规划。其中,作为遍历所有可达节点的A*算法,利用估价函数进行路径最优搜索。估价函数如式(1)所示。
f(n)=g(n)+h(n)
(1)
式中:n为当前节点;g(n)为起始点到当前节点n之间实际花费的代价值;f(n)为n的估价函数;h(n)为当前节点到目标点之间的估计代价值用启发函数。
A*算法流程如图1所示。图1中:将节点S记为自动化机器人的初始点、节点N记为当前总代价f(n)最小的节点;将M记为由节点N扩展得到的子节点;用O表示机器人移动的目标节点。

图1 A*算法流程图
由图1可知,基于改进的A*算法进行路径搜索时,首先需要确定已经搜索的节点与未进行搜索的节点。CLOSE表用于存放已经搜索的节点。OPEN表用于存放未经搜索的节点。具体步骤如下。①在OPEN表内保存初始节点S,并对表内是否出现未进行搜索的节点展开判断。如果存在未搜索的节点,意味着机器人路径搜索失败。②确定OPEN表内无初始节点S之外的未搜索节点,需要将总代价最小的节点N移动到CLOSE表内,并与目标节点O进行比较。当节点N与节点O一致,意味着机器人路径规划搜索完成。否则,需要对节点N展开八个方向的扩展,以此获取相应的子节点M,并对节点的总代价值进行计算。③对子节点M是否存在OPEN表内进行判断。当OPEN表内具有子节点M时,展开OPEN表内其他节点总代价值与子节点M的总代价值对比,然后对OPEN表进行更新。否则,需要继续判断子节点M是否已被搜索。如子节点M已被搜索,则去除节点M,访问M之外的节点;如子节点M未被搜索,则需要将节点M置于OPEN表内继续循环,直至路径搜索失败或是最优路径规划成功。
1.2 基于人工势场法的局部路径规划
本文针对自动化机器人处于外界环境信息不固定的情况开展路径规划。此次研究提出了采用改进的A*算法进行全局路径最优规划,以及采用人工势场法进行局部路径最优规划。改进的A*算法的优势在于能够去除移动路径的冗余点,继而有效缩短路径长度,并通过动态平滑处理获取预定路径。根据改进的A*算法得到的预定路径以及路径变化的环境信息,并通过人工势场法进行局部路径寻优,可对自动化机器人的路径规划进行实时调整。人工势场法如图2所示。

图2 人工势场法示意图
人工势场法的核心思想为:通过路径环境中的障碍物与目标构建虚拟的斥力场和引力场,并在二者的势场下保证能够实时进行障碍物规避,进而完成对预定目标位置的移动。其中,环境信息中的障碍物对自动化机器人的斥力因二者距离的增大而减小,而目标位置对自动化机器人的引力则因二者距离的增大而增大。假设二维空间区域为自动化机器人的运行空间,则人工势场法的函数定义如式(2)所示。
F(q)=Fatt(q)+Frep(q)
(2)
式中:Frep(q)为斥力势场函数;Fatt(q)为引力势场函数。
环境信息中的机器人与目标位置之间产生的引力会因为二者距离的增大而增大,因此机器人与目标位置之间的引力势场的势能也会逐步增大,并随着二者之间距离的减小而减小。当机器人与目标位置之间的引力势能缩减至特定值时,表示机器人实现对目标的跟踪。虽然传统人工势场法能够为机器人提供安全且平滑的路径规划,但算法自身的局部极小值缺点对机器人路径规划寻优产生影响。局部极小值对机器人运动的影响如图3所示。

图3 局部极小值对机器人运动的影响
由图3可知,局部极小值对自动化机器人路径规划寻优产生的影响是指:当障碍物环境信息中的目标对机器人产生的引力与障碍物对机器人产生的合斥力相等且方向相反时,由于此时机器人所受的合理为0,会出现来回振动现象,进而影响机器人向目标位置的移动[8]。同时,传统人工势场法只考虑环境信息中的障碍物、目标位置、与机器人之间的相对距离,忽视了其间的相对速度因素的影响,且传统人工势场法环境信息中的障碍物与目标位置还是静态的,无法满足自动化机器人动态运行环境的需求[9]。鉴于此,本文提出改进的人工势场法。其函数定义详见式(3)。
(3)
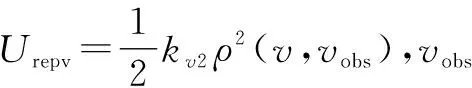
1.3 基于滑膜算法的轨迹跟踪控制
本文采用改进的A*算法实现了对机器人全局路径规划,又通过改进的人工势场法完成了局部路径规划,为自动化机器人提供了光滑且安全的运行路径。传统滑膜控制算法由于其整体控制律的非连续性,使得控制过程难免产生输入抖振的问题,继而影响系统的稳定性。
鉴于此,在轨迹跟踪层面,通过设计控制器,构建基于干扰观测器的自适应滑模控制器。其主要作用在于既改善了传统滑模控制器存在的输入抖振问题,又实现了在线调节控制系统的参数,继而确保了自动化机器人的轨迹跟踪控制。
控制器结构原理如图4所示。

图4 控制器结构原理图
由图4可知,滑膜控制器的设计过程分为两个部分:一是设计切换函数s(t),即通过比例积分(proportional integral,PI)滑膜面进行滑模面的设计;二是设计控制律τ,包括等效控制律和切换控制律。其中,滑膜面s(t)与控制律τ的定义详见式(4)。
(4)
式中:ec为速度误差。
与其他机器人轨迹跟踪控制算法相比,基于干扰观测器的自适应滑模控制算法不仅结构简单,而且具有较强的抗干扰能力与较快的动态响应[10]。
2 自动化机器人轨迹跟踪与路径规划结果分析
2.1 A*算法的全局路径规划仿真
为了解决了自动化机器人在多种复杂环境下的路径规划问题,针对改进的A*算法与传统算法进行对比仿真对比分析。改进的A*算法的全局路径规划仿真结果如图5所示。图5中,横坐标为横的位置x;纵坐标为纵的位置y。

图5 改进的A*算法的全局路径规划仿真结果
由图5(a)与图5(b)可知,较之于传统算法,采用改进后的A*算法进行机器人路径规划时,转弯角度减少了37.43%,路径长度减少了2.21%,因而有效删除了路径中的冗余点与运行折线,实现了路径优化。由图5(b)与图5(d)可知,采取改进的A*算法可利用平滑曲线替代折线运行,为机器人设计了安全且平滑的最优路径。
2.2 人工势场法的局部路径规划仿真
针对环境信息为动态障碍物与动态目标的状况下,采用改进后的人工势场法进行机器人局部路径规划。
人工势场法的局部路径规划仿真结果如图6所示。

图6 人工势场法的局部路径规划仿真结果
由图6(a)、图6(b)可知:传统人工势场法下,在障碍物附近的机器人出现不良震荡现象,运行时间为运行时间为8.645 s,路径长度为30.8 m;而改进后的人工势场法下,运行时间为7.035 s,路径长度为15.0 m。因此,较之于传统人工势场法,改进后的人工势场法进行机器人局部路径规划时,运行时间降低了18.6%,路径长度降低了51.3%。由图6(c)、图6(d)可知:在特殊环境下,采用传统人工势场法,机器人难以实现快速躲避障碍物,且震荡徘徊在局部极小值位置,运行时间为5.393 s,路径长度为48.0 m;采用改进后的人工势场法,不仅运行时间降低了59.13%、路径长度降低了52.3%,而且面对局部极小值位置时,机器人通过虚拟子目标生成外力,进而有效避免了在障碍物附近震荡,可有效绕过局部极小值陷阱区域。
2.3 自适应滑模控制器仿真分析
本文基于干扰观测器,构建自动化机器人轨迹跟踪自适应滑膜控制算法,并在MATLAB环境下对自动化机器人的轨迹跟踪展开仿真分析,以此验证算法的有效性。自适应滑模控制算法仿真结果如图7所示。
仿真结果显示,该算法策略控制下,自动化机器人的跟踪误差能够保证快速收敛为零,同时又提高了系统的鲁棒性。图7(a)和图7(b)分别描述了自动化机器人的位姿跟踪情况。基于干扰观测器,构建的自动化机器人轨迹跟踪自适应滑膜控制算法,在外部干扰和未建模动态同时存在的情况下,依然可以很好地跟踪期望轨迹。
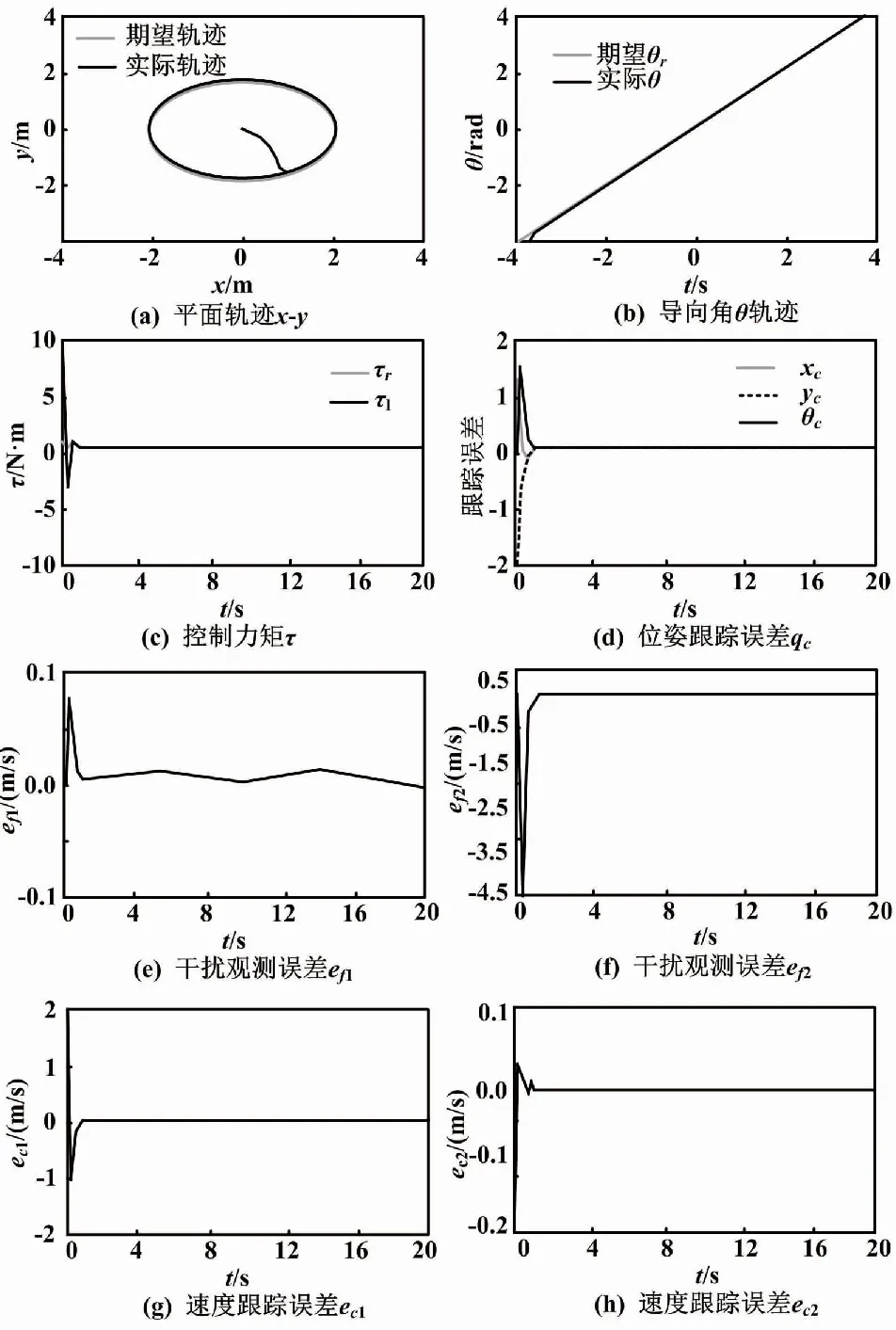
图7 自适应滑模控制算法仿真结果
图7(c)描述了自动化机器人控制力矩的输出情况。该算法有效降低了控制结构的抖振问题。图7(d)、图7(g)、图7(h)分别描述了机器人速度跟踪误差与位置跟踪误差的仿真情况。
而图7(e)与图7(f)描述了干扰观测器的观测误差。在自适应滑膜算法控制下,观测误差同样能够快速收敛到零。该结果验证了基于干扰观测器构建的自适应滑膜控制算法既能有效降低跟踪误差,又能有效提升机器人轨迹跟踪的收敛速度。
3 结论
自动化机器人广泛应用于各个领域,并根据轨迹跟踪与路径规划完成很多复杂任务。然而,面对运动过程中的非完整约束的制约,采取一般算法难以实现控制目的。针对环境信息不固定状况下自动化机器人的路径规划问题,采取改进的A*算法进行全局路径寻优,并采取改进的人工势场法进行局部路径寻优;同时,针对未建模动态与外部扰动自动化机器人轨迹跟踪控制问题,提出干扰观测器的自适应滑模控制算法。
仿真结果显示,较之于传统算法,采用改进后的A*算法进行机器人路径规划时,转弯角度减少了37.43%,路径长度减少了2.21%,不仅有效删除了路径中的冗余点与运行折线,而且利用平滑曲线替代折线运行,最终为机器人设计了安全且平滑的最优路径。较之于传统人工势场法,采用改进后的人工势场法不仅使运行时间降低了59.13%,而且使路径长度减少了52.3%,有效弥补了传统人工势场法的缺点与不足。而通过结合干扰观测器构建的自适应滑膜控制器,既能减轻滑膜控制中的输入抖振问题,又能根据实际需求调节观测逼近时间,继而实现了自动化机器人轨迹跟踪在线估算最优增益。

