基于惯量辨识的永磁同步电机PI自整定控制

宗学军， 高芮， 何戡

(沈阳化工大学 信息工程学院，辽宁 沈阳 110142)

0 引 言

永磁同步电机具有转矩密度高、损耗小和精度高等优点，在伺服和新能源汽车领域有广泛的应用。随着电机运行时间的增加和环境的变化，电机参数会出现不确定性，从而降低系统的控制精度。因此，精确辨识出电机参数对系统的控制性能有着重要意义[1]。为了提高电机的控制性能学者们已经进行了大量研究[2-4]。在系统参数中，转动惯量影响速度环的响应性，对速度环PI参数的调整具有指导意义。如果能够获得转动惯量值,将其应用于控制系统中，速度环控制的动态性能将得到改善。

电机运行时，转动惯量辨识方法有最小二乘法、模型参考自适应法和卡尔曼滤波法等[5-7]。最小二乘法的设计和实现相对简单，只需要改变算法中每个矩阵和向量的维数，但是容易形成“数据饱和”现象，引入遗忘因子可消除该问题。模型参考自适应法参数较多，导致自适应律的设计较为困难，对参考模型准确性的要求和依赖性较高；卡尔曼滤波法在识别转动惯量之前，需要应用泰勒公式对非线性方程进行近似线性化，增加了算法的复杂性和计算量。

本文采用带遗忘因子的最小二乘法对转动惯量在线辨识，辨识后的结果计算得到惯量比，将其用于速度环设计，以实现速度环的增益自动调节，从而提高速度环的响应性。

1 PMSM模型

永磁同步电机在d-q轴系下的电压方程：

(1)

磁链方程：

(2)

电磁转矩方程：

(3)

机械运动方程：

(4)

Te=Ktiq

(5)

式中：R为定子电阻；ud、uq、id、iq、Ld、Lq分别为d-q轴下定子电压、电流和电感；ψd、ψq、ψf分别为d-q轴下定子磁链和永磁体磁链；ωe为电角速度；pn为极对数；ω为机械角速度；J为转动惯量；B为黏滞摩擦因数；Te为电磁转矩；TL为负载转矩；Kt为转矩常数。

2 最小二乘转动惯量辨识

考虑线性回归方程：

y(k)=φT(k)θ+v(k)

(6)

式中：θ为参数向量；φT(k)为信息矩阵；v(k)为噪声向量；y(k)为系统输出向量。

构建目标函数：

J(θ)=[y(k)-φT(k)θ]2

(7)

(8)

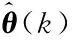
最小二乘法在实现过程中，数据进行不断递推迭代，往往会出现刚采集的新数据还未递推就淹没在之前的旧数据中，即“数据饱和”现象，导致数据更新能力变差。对于含有时变参数的系统，跟踪时变参数的准确性很重要，为此引入遗忘因子。带遗忘因子的递推最小二乘法是用新观测的数据不断修正以前的估计结果，用遗忘因子的权重修正新老数据的比例，以提高辨识精度。为了获得新的估计，带有遗忘因子的递归最小二乘法的表达式是:

(9)

式中：λ为遗忘因子。通过迭代更新获得所需的辨识参数。λ的取值范围通常在0.9～1之间。

为了方便永磁同步电机转动惯量的辨识，在仿真过程中，设黏滞摩擦因数B=0，式(4)可简化为

(10)

式(10)离散化处理得到：

(11)

式中：Ts为离散周期。

同理，前一周期为：

(12)

由于采样周期较短，负载转矩在一个采样周期内保持不变，即

TL(k)=TL(k-1)

(13)

由式(11)、式(12)与式(13)可得到：

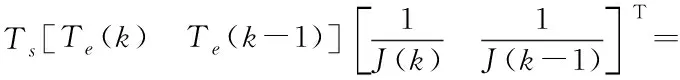
(14)

定义：

y(k)=ω(k)-2ω(k-1)+ω(k-2)

(15)

(16)

(17)

可得到：

y(k)=φT(k)θ

(18)

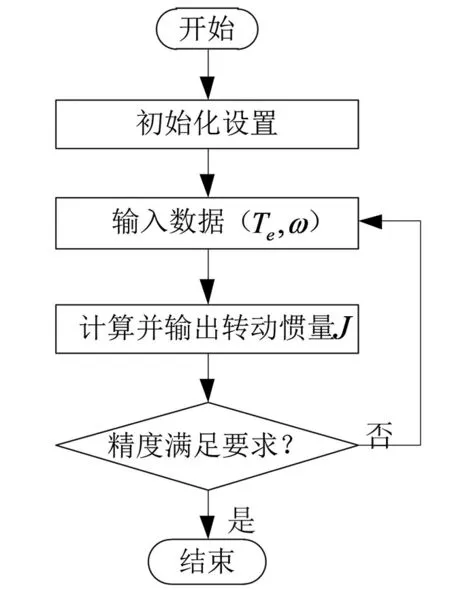
图1 辨识流程图

3 速度环参数自整定

转动惯量辨识的目的是通过惯量变化对速度环参数进行实时调整，优化速度环的转换结构，提高转速转换的响应性。在伺服系统中，由于电流环的带宽远大于速度环带宽，将电流环等效为一阶惯性环节。速度环控制框图如图2所示。

图2 速度环控制框图

(19)

速度环是一个典型的Ⅱ型系统，设计系统参数关系为：

Tω=hTi

(20)

(21)

式中：K为开环增益；h为中频带宽，根据系统的性能指标，这里取h=5。

速度环PI参数为：

(22)

(23)

式中：Kωi为速度环积分系数。

当电机带有负载运行时，系统总的转动惯量J为：

J=J0+JL

(24)

式中：J0为电机本体转动惯量；JL为负载转动惯量。令负载与电机本体转动惯量的比值为负载惯量比KJ，即

(25)

由式(22)、式(23)与式(25)可得，PI参数可化为：

(26)

(27)

将辨识后的惯量比KJ代入式(26)、式(27)中，对速度环PI参数不断修正，实现伺服系统的PI自整定功能。

4 仿真结果与分析

PMSM转动惯量在线辨识系统结构图如图3所示，包括速度控制回路、电流控制回路、坐标变换和转动惯量辨识模块。速度环采用PI控制，输出为转矩电流的给定iq，采用id=0的矢量控制，直轴电流的给定为0。电流环也采用PI控制，输出为d-q轴下的电压信号，其经过矢量变换、电压空间矢量调制生成PWM脉冲信号驱动电机运行。

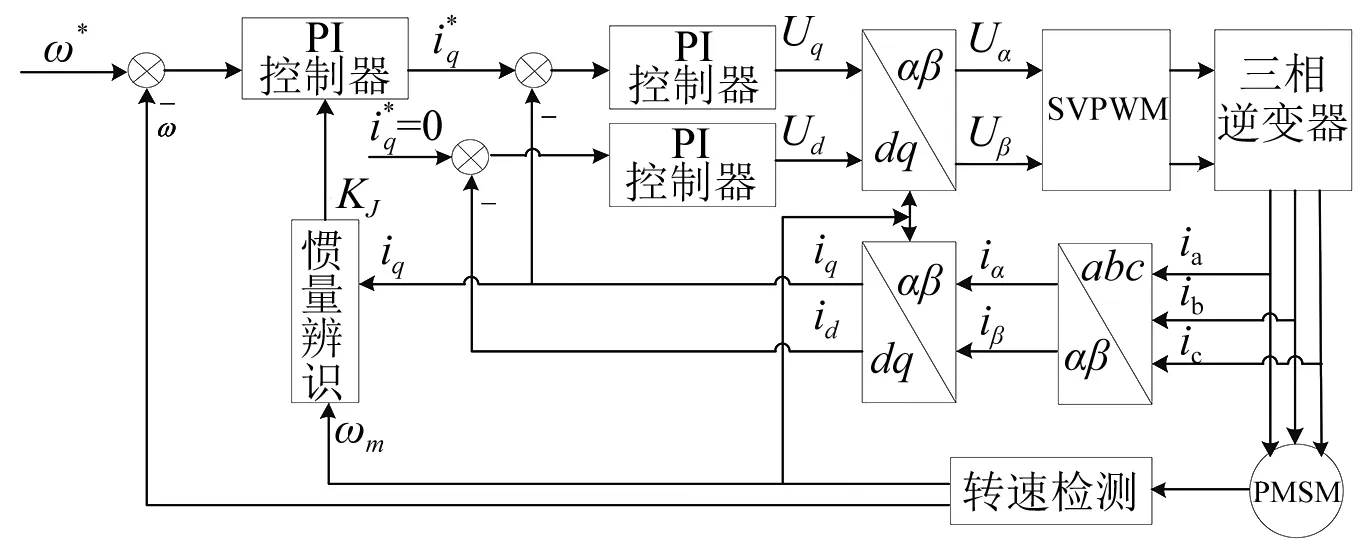
图3 系统结构图

采用PMSM矢量控制的离散系统模型进行仿真，选用基于TMS320F28335试验平台作为伺服驱动系统[8]。采样周期为0.1 ms，极对数为4，定子电感Ls=4.05 mH，定子电阻R=0.46 Ω，永磁体磁通ψf=0.08 Wb，电机本体转动惯量J0=0.000 106 kg·m2。

速度信号为-500～500 r/min交替变化的正弦波，频率为50 Hz。电机空载运行时，没有机械负载，仅估算或计算裸转子的转动惯量J，空载时，系统总的转动惯量J=J0=0.000 106 kg·m2；系统加入给定转动惯量JL=0.000 318 kg·m2，此时有J=J0+JL。图4为λ=0.96、λ=0.98、λ=0.99时转动惯量的辨识结果。从辨识结果可以看出，遗忘因子λ对辨识结果影响较大。遗忘因子越小，系统波动越大；λ取0.99时，系统跟踪效果最好，曲线平稳运行，上下波动小。

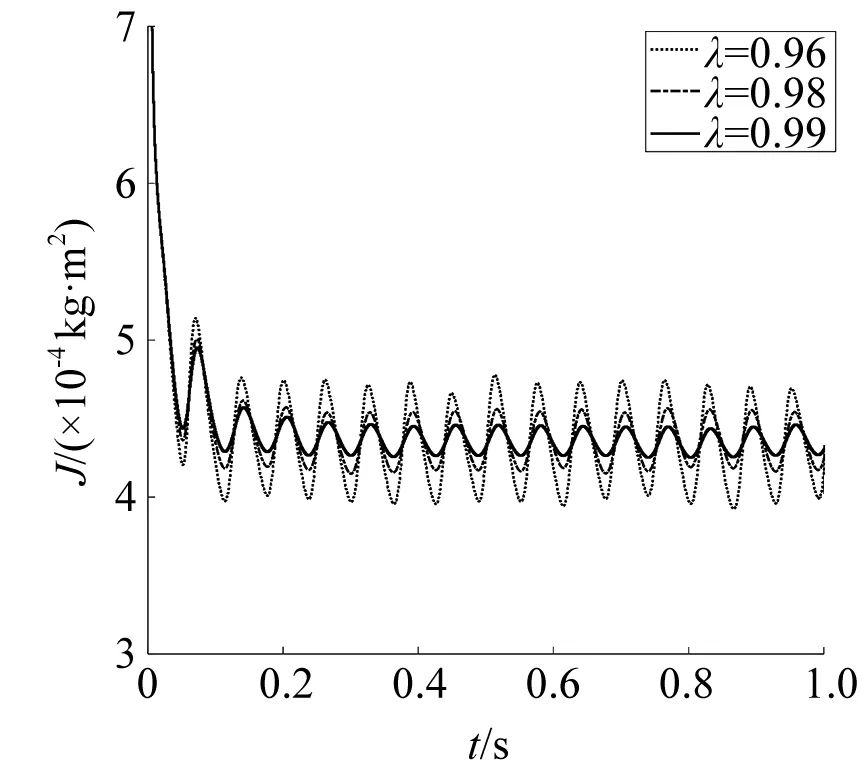
图4 转动惯量辨识结果

λ=0.99时，转动惯量的辨识估计值最接近其真实值，且辨识误差较小，以下均采用该遗忘因子。系统分别加入给定负载转动惯量JL=0.000 318 kg·m2、JL=0.000 848 kg·m2时，电机惯量比如图5所示。仿真结果表明，此方法可准确地在线辨识出转动惯量。

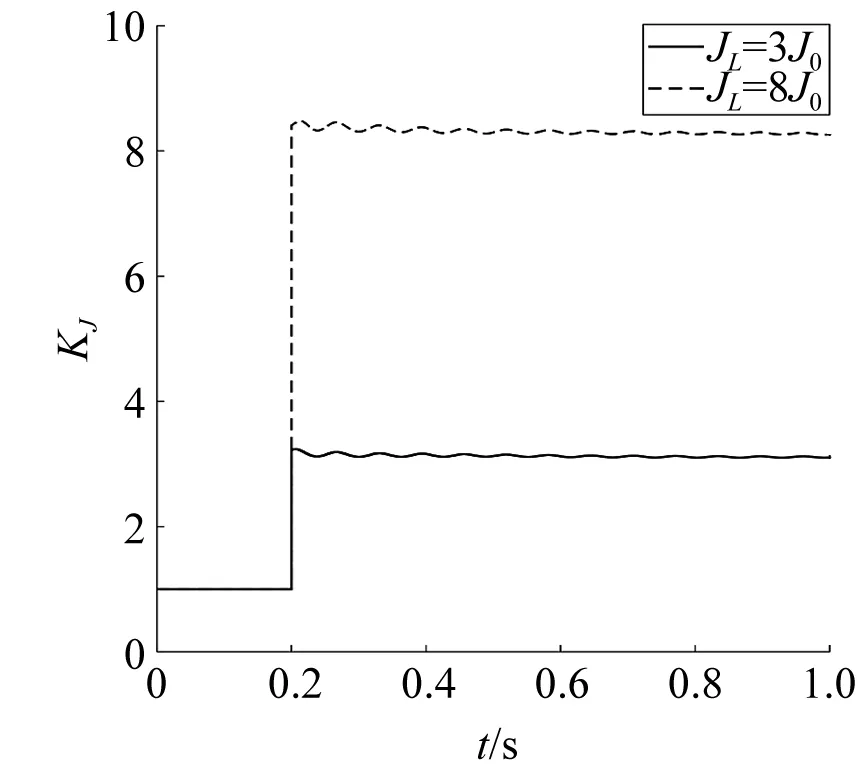
图5 电机惯量比

为了验证惯量比对系统响应性的效果，采用传统速度环PI控制与惯量比控制分别对系统模型进行仿真试验。给定JL=8J0时，速度变化跟踪曲线如图6所示。仿真结果可以看出：传统PI控制方式下，实际速度响应与给定速度有一定误差，精度不够准确；引入惯量比实时调整速度环PI参数时，实际速度与给定速度响应一致，结果精确，证明辨识后的惯量比引入速度环PI控制中是有效且准确的，即该方法保持了一定的性能。

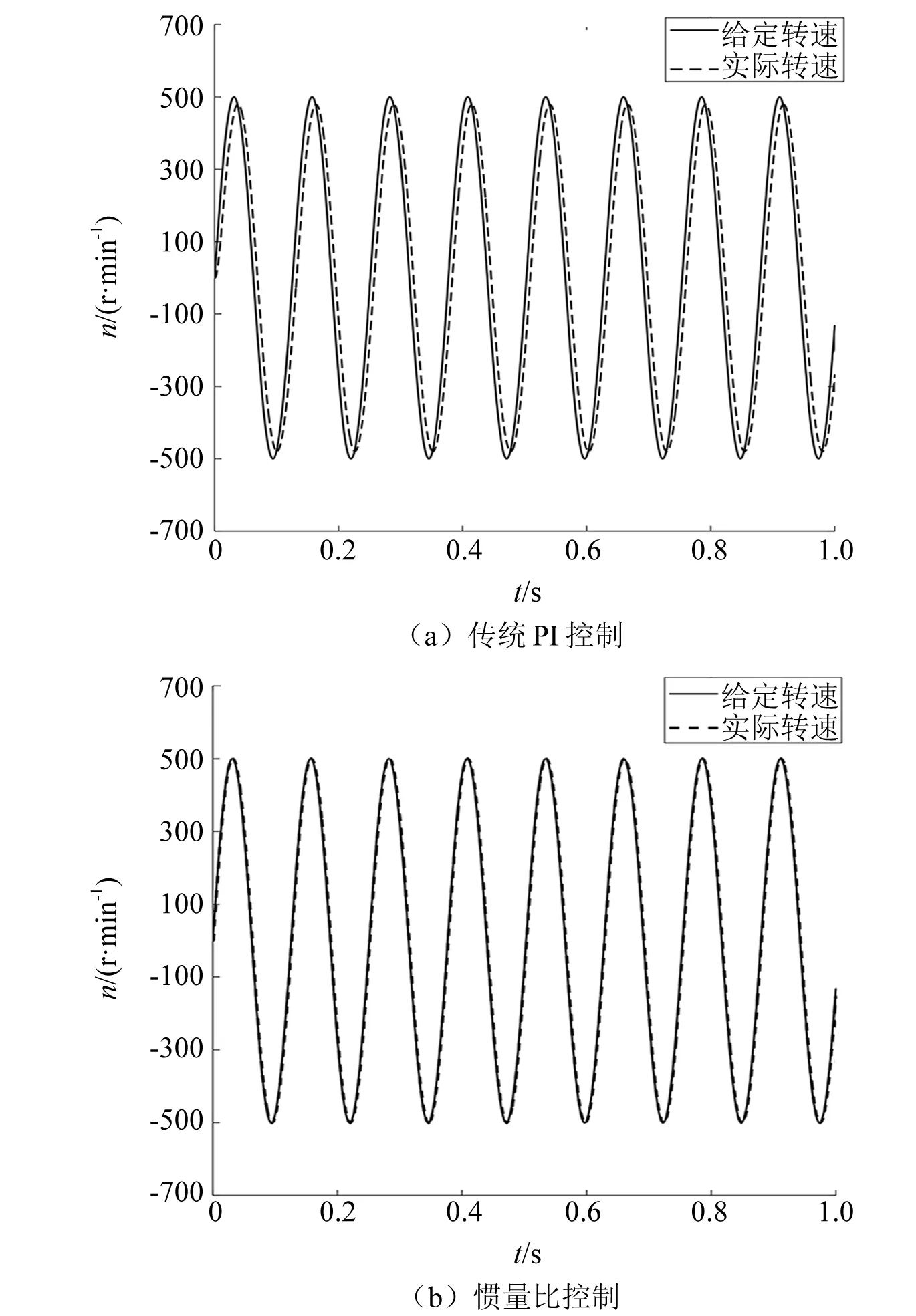
图6 JL=8J0速度变化跟踪曲线

5 结束语

本文采用基于惯量辨识的速度环PI自整定控制方法。在系统转动惯量变化时，采用带遗忘因子的最小二乘法对PMSM转动惯量进行在线辨识。仿真结果证明了在线辨识方法的收敛性和准确性。给定不同负载惯量时，辨识得到的转动惯量与电机本体转动惯量计算得到惯量比，将该惯量比引入系统速度环对其进行PI参数自整定控制。与传统速度环相比，该控制方式能够提高速度给定值的跟踪准确性和跟踪精度，优化速度转换结构，提高转速转换的响应性，从而提高系统参数变化时的稳定性。