超导转变边沿探测器梁架尺寸估算方法*
高冠华 徐郁 廖国福 卢方军
1) (中国科学院高能物理研究所,粒子天体物理重点实验室,北京 100049)
2) (中国科学院大学,北京 100049)
由于具有极低的噪声等效功率,超导转变边沿探测器(transition edge sensor,TES)近年来被广泛地应用于国际各个宇宙微波背景辐射(cosmic microwave background,CMB)极化观测项目中.为保证探测器工作在性能最佳区间,探测器饱和功率值需根据观测地点气象条件及观测波段进行调整,而探测器梁架结构尺寸直接决定了饱和功率大小.因工艺差异等原因,不同加工方案下得到的梁架尺寸参数往往不能直接用于横向比对.在之前的观测项目中,一般先加工出一系列不同尺寸器件并逐一测量,然后通过拟合实测饱和功率与梁架尺寸的关系推测实际需要尺寸.为了与目标值匹配,往往需要多次加工迭代过程.本文使用边界限制的声子输运模型,成功整合了之前观测项目中的器件参数,对TES 梁架尺寸进行预估.并按照预估值首次在国内制备了用于探测CMB 极化信号的TES 探测器芯片.测量表明参数与目标值相差较小.该方法可以很好地对同类TES 探测器尺寸进行估计,对之后TES 探测器的设计有指导性意义.
1 引言
宇宙微波背景辐射作为宇宙大爆炸后早期冷却过程产生的遗留痕迹,保留了丰富的宇宙早期信息.被发现之后,历经COBE[1],WMAP[2],Planck[3]等卫星的观测,人们发现宇宙微波背景辐射(CMB)信号在温度上存在着微小的各向异性.
因为CMB 产生时宇宙还处于早期高密度高温度的状态,各类物质都聚集在一起,所以其各向异性的信息可以对大量宇宙学参数和宇宙学模型产生强有力的约束,诸如中微子质量、暗物质模型、暗能量模型等[4].其中,最后散射面上温度波动的四极矩会导致无极化光子在发生汤姆孙散射时转变为极化光子,而只有张量扰动即引力波波动才会导致其极化分布产生B 模式图样,所以CMB 偏振测量也成为了探测原初引力波与验证引力量子涨落的核心数据来源[5].
根据Planck 卫星的观测结果,CMB 信号中的各向异性成分占总量的 1/100000 以下[6].同时CMB的各向异性成分中,只有B 模式才来自于原初引力波成分.而根据近年来对CMB 极化观测的结果,B 模式与E 模式比例即张标比r <0.009[7].所以为了能够进一步提高对B 模式的探测能力,需要使用拥有极低噪声等效功率(noise equivalent power,NEP)的探测器进行探测.
超导转变边沿探测器(transition edge sensor,TES)作为一种新型热平衡探测器,依靠将输入能量转化为温度变化量来进行测量.相比传统的CCD 和CMOS 等电离型探测器,其工作时不存在电荷收集过程,可以有效规避电离过程产生的统计涨落噪声[8],因此被大量应用于单光子探测领域[9].同时因为TES 工作状态下噪声主要来源于温度涨落带来的声子噪声,而TES工作温度一般<1K,所以其可拥有极低的NEP,典型值<75近些年来TES 加工工艺逐渐发展成熟,可以制备成用于巡天观测的大规模阵列,被BICEP2[11],BICEP3[12],POLARBEAR[13],SPIDER[14],ACT Pol[15],Advanced ACTPol[16]等项目选为CMB 极化探测的核心探测器.
对于用于CMB 探测的TES 探测器,其饱和功率需要适应观测条件,可适用范围小.在观测中,器件实际饱和功率过小会导致TES 探测器线性度变差直至无法正常工作,过大则会导致NEP 上升探测精度下降.目前TES 探测器的加工过程通常由微加工工艺来实现,器件实际饱和功率由探测器梁架尺寸决定.因此TES 探测器物理尺寸设计对最终探测器性能有着决定性影响.由于工艺差异、材料差异等原因,不同加工方案下得到的梁架尺寸参数往往不能直接用于横向比对.在之前使用了TES 探测器的各个CMB 观测项目中,一般先加工出一系列不同尺寸器件并逐一测量,然后通过拟合实测饱和功率与梁架尺寸的关系推测实际需要尺寸[17,18].在实际操作过程中,这样的方法成本较高,往往需要多次加工迭代,测试时间过长.本文选择使用边界限制的声子输运模型,整合了之前研究项目得到的测试数据,对TES 梁架尺寸进行提前预估.在加工工艺上,通过反复进行工艺摸索与测试,首次在国内制备了用于探测CMB 极化信号的TES探测器芯片.在按照估计尺寸进行芯片加工后,通过对器件的实际测量可知,探测器饱和功率实测值与计算值相差较小.该种设计方法可以很好地对TES 探测器尺寸进行估计,减少加工与测试时间,对之后同类TES 探测器的设计有指导性意义.
2 TES 探测器基本原理
作为一种热探测器,从热结构上进行功能划分,TES 探测器核心结构主要分为4 部分:超导薄膜、吸收体、弱热连接和热沉.
首先,超导薄膜是TES 探测器输出电信号的来源,也是TES 探测器低噪声的关键.一个理想的超导转变曲线如图1(a)所示,其中Rn为超导薄膜常态电阻,薄膜电阻 0.1Rn— 0.9Rn所对应的温度区间为转变区间,转变区间中心温度为转变温度Tc.随着温度的升高,超导薄膜在转变区间内快速地由超导态转变为正常态,电阻急剧升高,从而产生输出信号变化.其次,由于TES 本质上通过探测温度变化来探测入射信号,而其所接收的输入信号的形式往往是高能光子或持续的微波信号,所以TES探测器需要各类吸收体结构先将入射能量转化为热量.再次,超导薄膜与热沉之间通过低热导结构相连构成弱热连接,从而建立稳定的温度梯度,控制热量的流向.最后,热沉结构可视为一个稳定的温度锚点,其温度Tb几乎不会随入射能量大小变化,用以保证系统基态稳定.在TES 探测器外部,通常还需要电压偏置电路来控制其静态工作点,并通过超导量子干涉器件(superconducting quantum interfence device,SQUID)对流过TES 的电流进行耦合与放大.通常情况下TES 探测器的整体框架如图2 所示.

图1 (a)超导薄膜理想R-T 曲线;(b) AlMn 材料实测R-T曲线Fig.1.(a) Ideal R-T curve of superconducting thin films;(b) measured R-T curve of AlMn alloy.
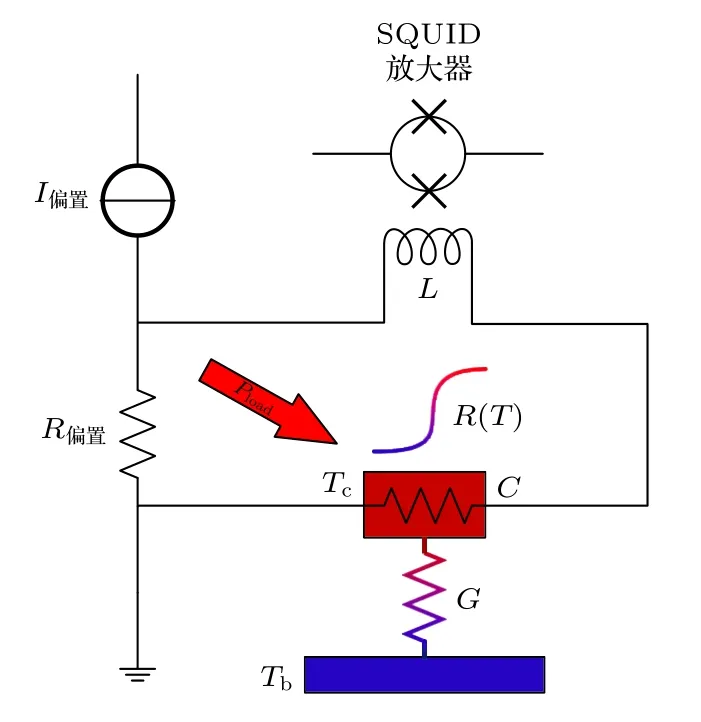
图2 TES 探测器框架示意图Fig.2.Schematic diagram of TES detector system.
在稳定状态下,超导薄膜的电阻被偏置电压控制在转变区间的中心附近(如图1(a)中T1点).电流流过超导薄膜产生的焦耳热PTES将其温度加热到T1,然后流过弱热连接进入温度为Tb的热沉.在电压偏置的条件下,考虑一个小幅入射噪声信号δE.噪声信号首先会在吸收体内转化为热量,带动超导薄膜温升至图1(a)中T2点导致其电阻变大,进而导致TES 发热功率降低.同时,在小幅度温度变化下,弱热连接的热导G可视为恒定,其导热功率因两端温差变大而变大.在发热功率降低的同时导热功率变大,超导薄膜因此降温回到T1位置.上述过程被称为TES 探测器的电热负反馈过程[8].
在CMB 观测过程中,固定观测方向的被观测信号可视为恒定功率信号P负载.此时入射功率信号转化为热流后与超导薄膜发热功率共同流经弱热连接.由于电热负反馈效应,总发热功率趋于恒定,超导薄膜发热功率降低并且电阻增加.由于输入功率恒定,可以假设此时系统稳定在图1(a)中T2点,通过测量流过TES 探测器的电流,可以测量入射功率大小.
在低温下,假设弱热连接两端温度分别为T与Tb,且T >Tb.则流经弱热连接的热功率P一般可以用如下方程描述[8]:
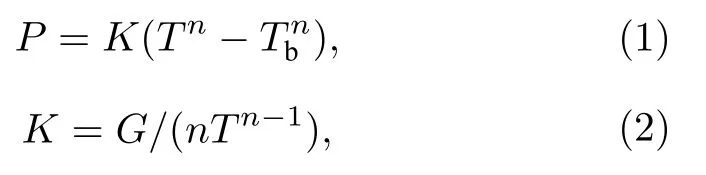
式中n为热指数,K为热系数,G为弱热连接的热导.其中假设了弱热连接的热导遵循G∝Tn−1的关系.热指数n主要由探测器中构成弱热连接的材料的导热机制决定.对于以电子传热为主导的金属材料,n≈2 .对于以声子传热为主的材料,n的值在3—4 之间[19].
在图1(a)中的两个工作状态T1与T2下,假设TES 两端偏置电压为V偏置,超导薄膜发热功率分别可表示为
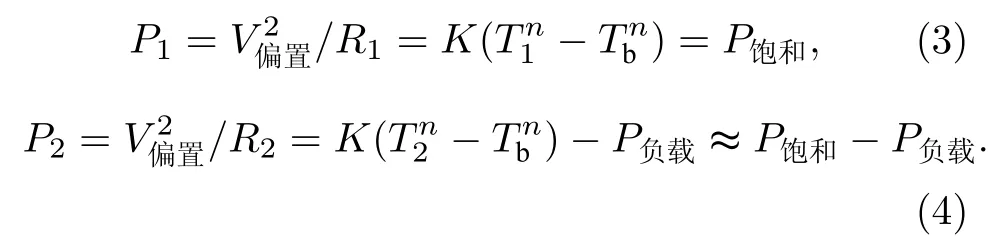
目前国际上使用的TES 探测器,其超导薄膜的转变温度一般在几百mK,区间宽度在10 mK以下[9,20].由于超导薄膜的转变区间非常窄,所以T1≈T2≈Tc.代入(3)式和(4)式可知,系统总热功率不变,信号输入功率约等于超导薄膜发热功率的减小量.因此TES 探测器所能探测的最大功率小于TES 的饱和功率P饱和即偏置点处发热功率.
对于CMB 观测,探测器最重要的参数为NEP.其定义为系统信噪比为1 时1 Hz 带宽下的输入功率量,即系统可探测到的最小功率.对于TES 探测器,公式为
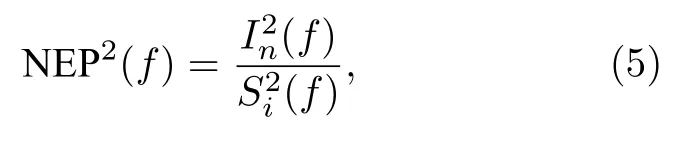
其中In(f)为探测器的等效输出电流噪声,Si(f)δI/δP为探测器电流响应率.TES 探测器的本征噪声成分中,由热涨落带来的声子噪声占据主导.在声子噪声主导下的 NEP 可由如下公式进行计算[19]:
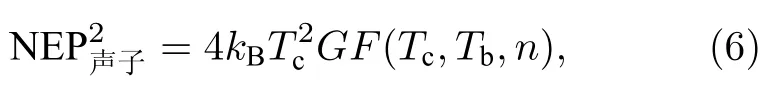
其中kB为玻尔兹曼常数.由(6)式可知,NEP 主要与,G,F成正比.其中Tc由超导薄膜性质决定,选用锰的质量分数为 200×10−6的铝材料(AlMn合金)作为超导薄膜材料,其Tc约为571 mK,转变区间宽度约为2 mK,典型R-T曲线如图1(b).图中数据通过四端法搭配温度步进控制得到.由于超导薄膜转变曲线与工作电流有关,测试中使用了100 µA的电流偏置.温度步进长度为50 µK,每次步进后恒温一段时间.图中曲线由大量实际测试数据点直接连线构成.转变区间中部的锯齿状结构来自于温度步进后恒温区间内超导薄膜电阻因准正反馈产生的噪声,噪声大小与超导薄膜对温度的灵敏度有关.在转变区间中段,电阻随温度变化最剧烈,所以曲线锯齿纵向尺寸最大.因此曲线上下边缘代表了对应温度点测得电阻的峰峰值.由于测量误差较小,且温度点众多,此处不再画出误差棒.(6)式中Tb为热沉温度,由制冷系统决定.由于一般情况下CMB 观测望远镜使用3He 吸附式制冷机进行制冷,所以该温度约为250 mK.F(Tc,Tb,n)为Tc,Tb和n的函数,在三者确定的情况下为常数,代入本文中的参数后F≈0.71 .因此为了有效降低NEP,需要降低热导G.但是从(1)式—(3)式可以看出,在降低热导G时,TES 静态工作点下的饱和功率也降低了.从上文可知,在电热负反馈过程中,最大可测量的入射功率小于饱和功率.在观测中,为了保证信号的线性度,TES 探测器的饱和功率需要约大于观测的最大输入功率值的两倍.输入功率最大值取决于观测地点的水汽状态,此处参考实际观测点的观测值及计算方法[10,21],设定使用过程中的P饱和值为15 pW.综上可以看出,当n由加工工艺唯一确定,此时的G也是唯一确定的,需要通过设计探测器尺寸来进行匹配.若实际加工得到的探测器饱和功率相比预计饱和功率过小,则探测器线性度不好或无法工作.若过大,则NEP 也会随之增大.
3 声子输运模型与模型参数选取
本文为CMB 观测设计的TES 探测器的立体图如图3(a)所示(为观察方便,图中省略了氧化硅介质层),整个结构通过微加工工艺实现.在之前的各个观测项目中[11,12,14−16],也都使用了相似的设计.该设计方案中,超导薄膜所在的“岛”结构被4 根“梁架”结构托起悬挂在硅支架上.鉴于氮化硅(SiNx) 材料优良的机械性能,岛结构与梁架结构通常使用 500 nm—1µm 厚的氮化硅作为其下层结构支撑材料与导热材料.超导导线与超导薄膜等上层结构则通过微加工的方法生长在氮化硅薄膜上.从功能上,整个岛结构作为吸收体,超导薄膜生长在岛结构之上,梁架结构作为弱热连接,外围的硅框架作为热沉.工作时,微波信号通过超导材料铌(Nb)制成的微带线从外部微波器件传入岛结构中的金(Au)制损耗线,转化为热量,加热整个岛结构.
从实际结构可知,弱热连接的热导G由梁架尺寸及材料决定.在过去的诸多国际CMB 观测项目中,一般采用穷举不同尺寸后实测的方法.在光刻版图中穷举所有的可能尺寸,加工得到器件后逐个测试热导G,最后通过拟合的方法得到最终的设计尺寸.该方法成本高且测试时间非常长.本文通过边界限制的声子输运模型来估算TES 探测器梁架结构尺寸.
由下一节介绍的微加工工艺制造的TES 芯片的梁架结构横截面如图3(b)所示.考虑到结构强度,本文选用氮化硅材料厚度为1 µm .在初始状态下,氮化硅下方为200 nm 厚的氧化硅(SiOx)截止层,其在深硅刻蚀步骤中被用作截止层,用以保护氮化硅层,最终被过刻蚀到50 nm 左右.在氮化硅上方是两层由铌(Nb)构成的导电层,用作微带线结构及TES 探测器的信号导线.两层铌材料中间为一层多孔氧化硅层作为绝缘介质层.在TES的工作温度下两层铌导线完全超导,正常态电子转变为库珀对,电子热导率贡献被压低,所以对总体热导率贡献极低[22,23].为了保证深硅刻蚀后岛结构不发生形变,以及降低梁架结构长度,加工中使用了电感耦合等离子体化学气相沉积(inductive coupled plasma chemical vapor deposition,ICPCVD)方法生长的多孔氧化硅层来同时保证材料低应力与低热导率.由参考文献[24]可知,相同温度下多孔氧化硅的热导率为氮化硅的1/4 以下.考虑到其厚度为300 nm,可估算其对总热导的贡献小于10%.由于为CMB 观测设计的TES 探测器的梁架横截面结构均相似[11,12,14−16],因此以下可以假设该设计结构中热量基本都经由氮化硅结构进行传输,而其他生长在氮化硅之上的材料通过对氮化硅产生寄生热容来影响热导率.下文将主要通过计算氮化硅结构的尺寸来对所需实际长度进行估算.
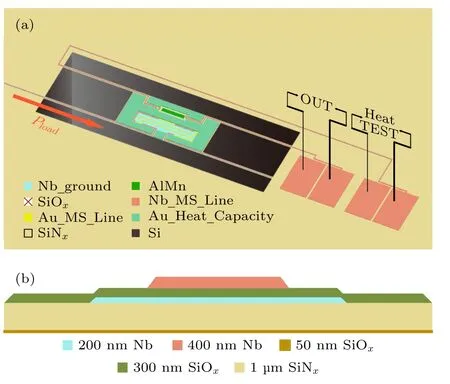
图3 (a) TES 探测器立体结构图;(b)梁架结构横截面示意图Fig.3.(a) Three dimensional (3D) structure of TES detector;(b) cross section of beam structure.
为了保障TES 探测器的岛结构及梁架结构在释放后不发生明显的翘曲,使用的氮化硅材料为硅氮比>3:4 的低应力无定形氮化硅,其主要通过声子进行传热,声子热导率可写为
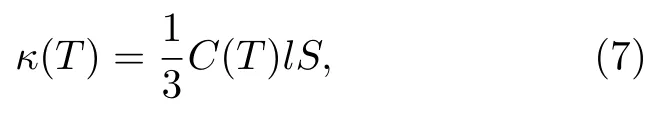
其中C(T) 为比热容,l为声子平均自由程,S为氮化硅中的平均声速.根据上文的假设,此处C(T) 为氮化硅热容与寄生热容之和,通常为温度的函数.
氮化硅中平均声速的计算公式如下:
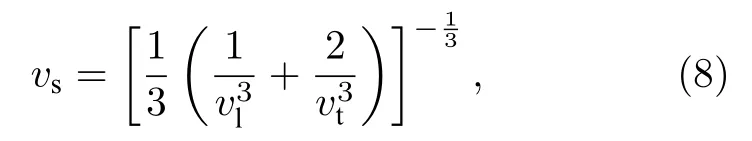
其中vl为纵波声速,vt为横波声速,参考文献[25]数 据vl1.115×104m/s,vt6.28×103m/s 得到vs6986 m/s.考虑到氮化硅结构细长,且尺寸相对较大,存在温度梯度.此时可以使用宏观传热的方法处理,由傅里叶定律

可计算热流密度JT,其中 dT/dx为温度梯度.假设梁架两端温度分别为Tb与Tc,梁架长度为L,方程两边同时对x进行积分,由于稳态下梁架所有横截面的热流密度相等且为常量,可以得到
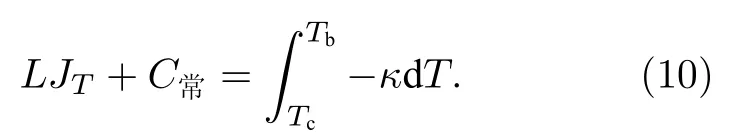
考虑到L趋近于零时,(10)式需要回归到(9)式,所以此处常数为零.因此对一条梁架而言,总传热功率可通过在其长度方向进行积分得到
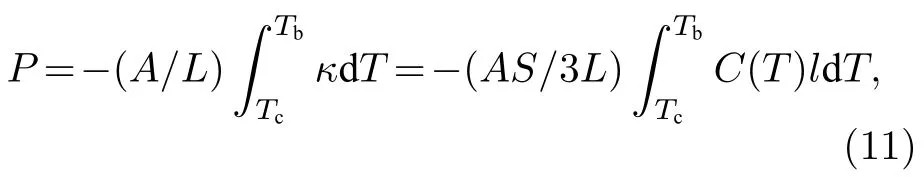
其中A为截面面积.热导率G由其定义可得
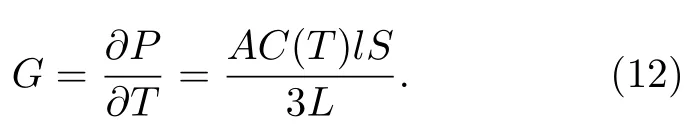
在一般情况下[19],取
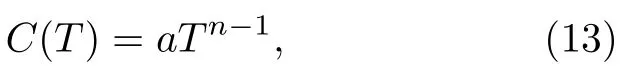
其中a为材料参数.将其代入(11)式可以得到之前(1)式的形式.对于无定形固体材料,低温下热容可以使用以下形式来细化描述[26]:

其中a,b取决于材料生长工艺.考虑到作为寄生热容产生的主要部分,多孔氧化硅层也属于无定形材料.所以总体热容也可以由该形式进行表示.将(14)式代入(11)式得到
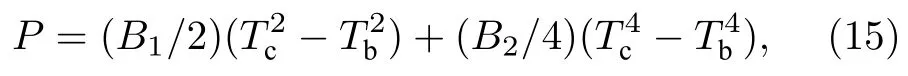
其中
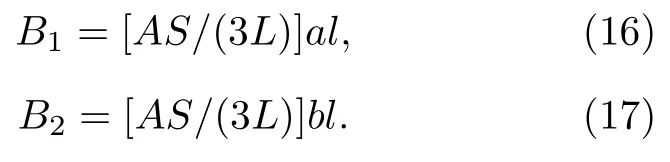
对于(15)式,通过测量在不同Tb下的同一TES探测器的饱和功率,即可拟合得到参数B1,B2.为了通过修改梁架尺寸来使饱和功率P饱和达到目标值,还需要得到对应尺寸下的声子平均自由程l.热导率主要取决于材料特性,而声子平均自由程主要取决于材料尺寸及表面状态.
根据之前其他实验及理论的结果,对于厚度为1 μm 的氮化硅梁架,需要考虑声子在氮化硅材料表面的边界反射所导致的平均自由程变化[23,27].本实验中,氮化硅梁架横截面宽度与厚度比m>5,同时由于梁架左右侧边缘是由干法刻蚀产生的侧壁,表面较为粗糙,可以假设声子在两个侧面上全部发生漫反射.所以此处主要考虑梁架上下两个表面的反射情况.在当前的情况下,声子输运过程可以相应简化,可以通过Sultan 等[28]修正的边界限制声子输运模型来计算该情况下声子的有效平均自由程l有效:
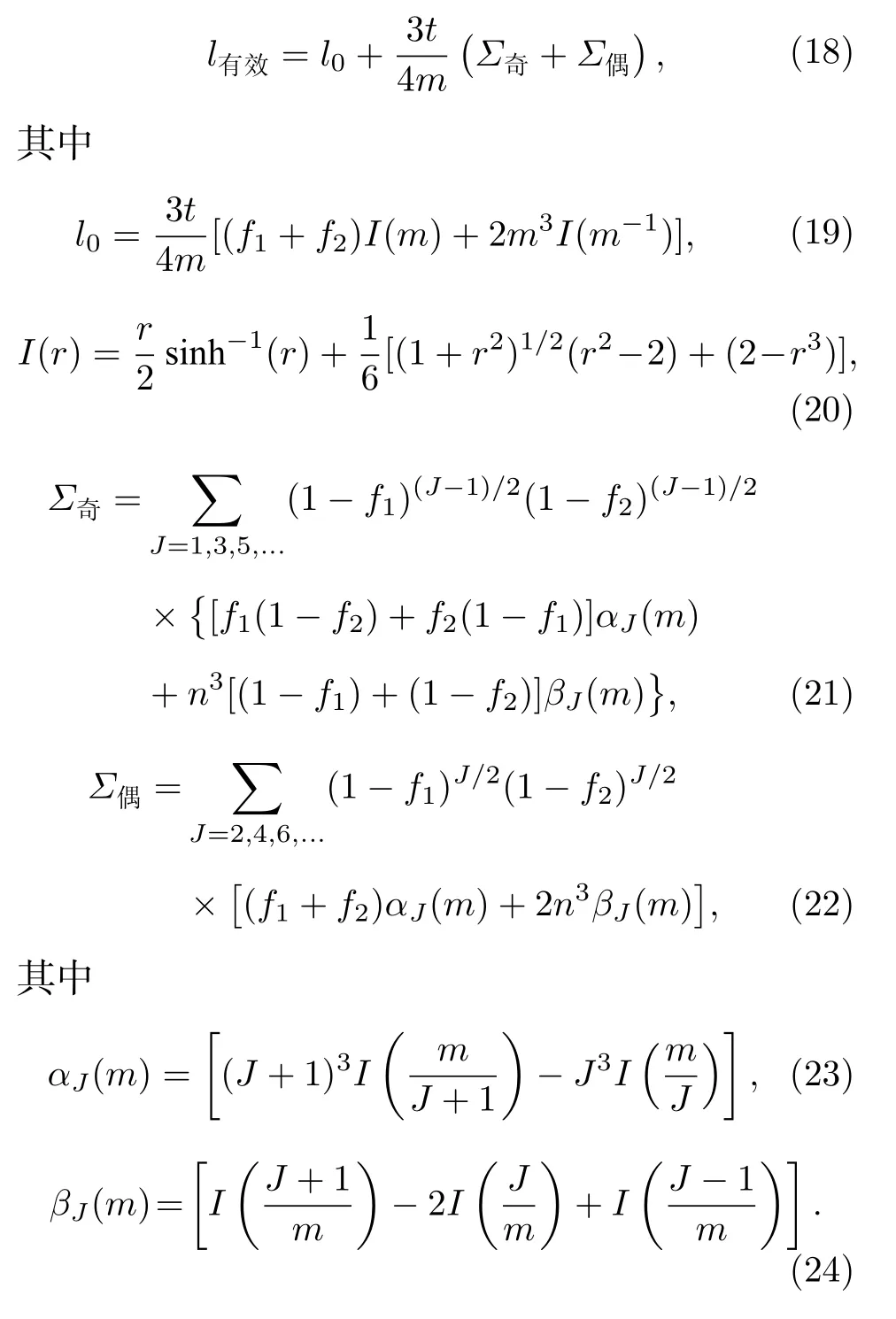
(18)式—(24)式中t为氮化硅厚度,m为梁架宽度与厚度之比,f1和f2分别为上下两个表面发生漫反射的概率(在不发生漫反射的情况下则发生镜面散射,材料表面越粗糙f值越大),J为声子的反射次数.l0来自于声子的弹道输运过程和两粗糙侧壁的一次反射.总反射次数为奇数次与偶数次的情况分别列出.从(18)式—(24)可以看出,l有效只与导热结构的横截面尺寸及材料表面状态有关,与长度和温度无关.由于计算较为复杂,所以采用数值计算的方法取求和部分的前200 项.公式中求和项随着反射次数J快速衰减,前200 项占总和的99.9%以上,且由于声子受尺寸限制不会无限次反射,故200 项之后可以忽略.氮化硅厚度为1 μm,假设上下两表面的漫反射概率同为f,不同宽度w下声子的有效平均自由程如图4 所示.
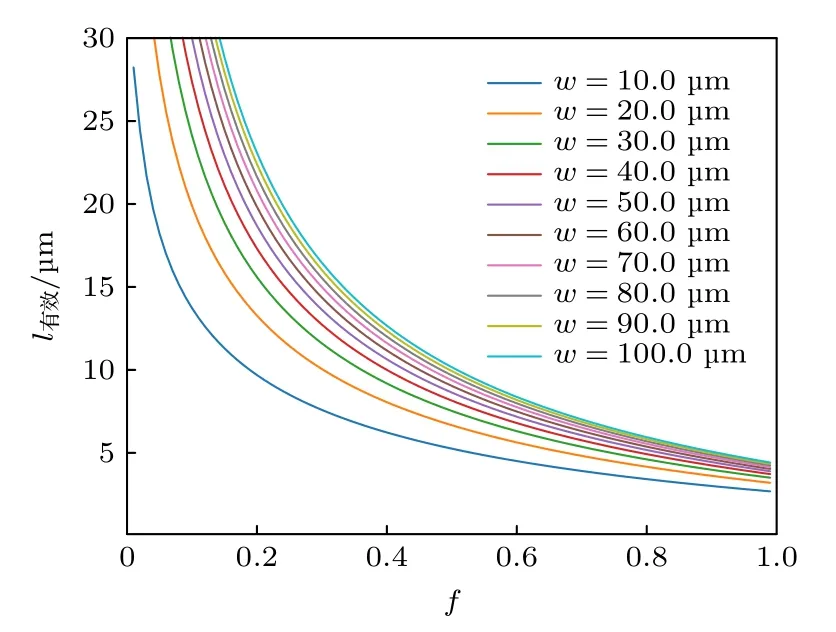
图4 不同梁架宽度下声子有效平均自由程与材料表面漫反射概率的关系Fig.4.Relationship between the effective mean free path of phonons and the probability of diffuse reflection on the material surface under different beam widths.
从图4 可知,相同的表面状态下,l有效随宽度增大而增大.考虑(15)式可知在相同材料的情况下,宽度增长带来的热导变化大于一般的线性增长.这与之前文献中的测试结论一致[17,23].由于加工工艺的限制,梁架结构过长会降低成品率.因此为了降低热导,需要让梁架宽度尽量窄.但是考虑到梁架上微带线的最小尺寸的限制,以及加工中光刻胶的涂覆均匀性的需求,最后选用氮化硅宽度为15 μm .
为了确定梁架的长度,还需要得到上文中各个与材料有关的参数值,同时数据来源需要考虑相应工艺过程.由于目前没有实验使用与本文完全相同的工艺用于参考,所以选择对l有效与C(T) 分别进行拟合.因为表面生长额外材料会明确地影响l有效[28],选用了ACTPol 项目的测试结果[17]用于拟合l有效,其工艺中氮化硅下方存在460 nm 厚的氧化硅截止层.同时由于本实验中产生寄生热容的部分相对较少,氧化硅介质层因特殊工艺产生的寄生热容较低,所以选用Wang 等[23]实验拟合得到的C(T) 进行计算,其所用工艺中无氧化硅介质层.
考虑到梁架需要足够长度才能满足多次反射的假设条件.选用ACTPol 测试中TES 梁架结构长度为500 μm,宽度分别为10 与15 μm 的TES探测器的测试结果,分别代入(15)式进行拟合.假设其上下两表面f值相同,可得到不同宽度下l有效的比值.代入(18)式后通过数值求解得到f ≈0.626 .这与Sultan 等[28]用其他实验方法得到的0.7 比较接近.而Wang 等[23]实验结果通过拟合得到的比热容值为C(T)0.083T+0.508T2J/(m3K),代入对应参数后数值求解得到的梁架长度约为1105.76 μm,为加工测试方便,取整为1100 μm .
4 TES 探测器芯片加工及测试结果
本实验中TES 探测器芯片加工工艺共9 次光刻,最终岛结构共包含8 层材料,加工周期约为6 个月.微波器件结构主要参考Advanced ACTPol项目以及Johnson 等的设计[16,29].使用4 英寸晶圆,单片晶圆内共97 个芯片单元.单个芯片单元尺寸为 7.6 mm×7.6 mm .其加工过程横截面示意图如图5 (截面垂直于TES 探测器梁架方向)所示.
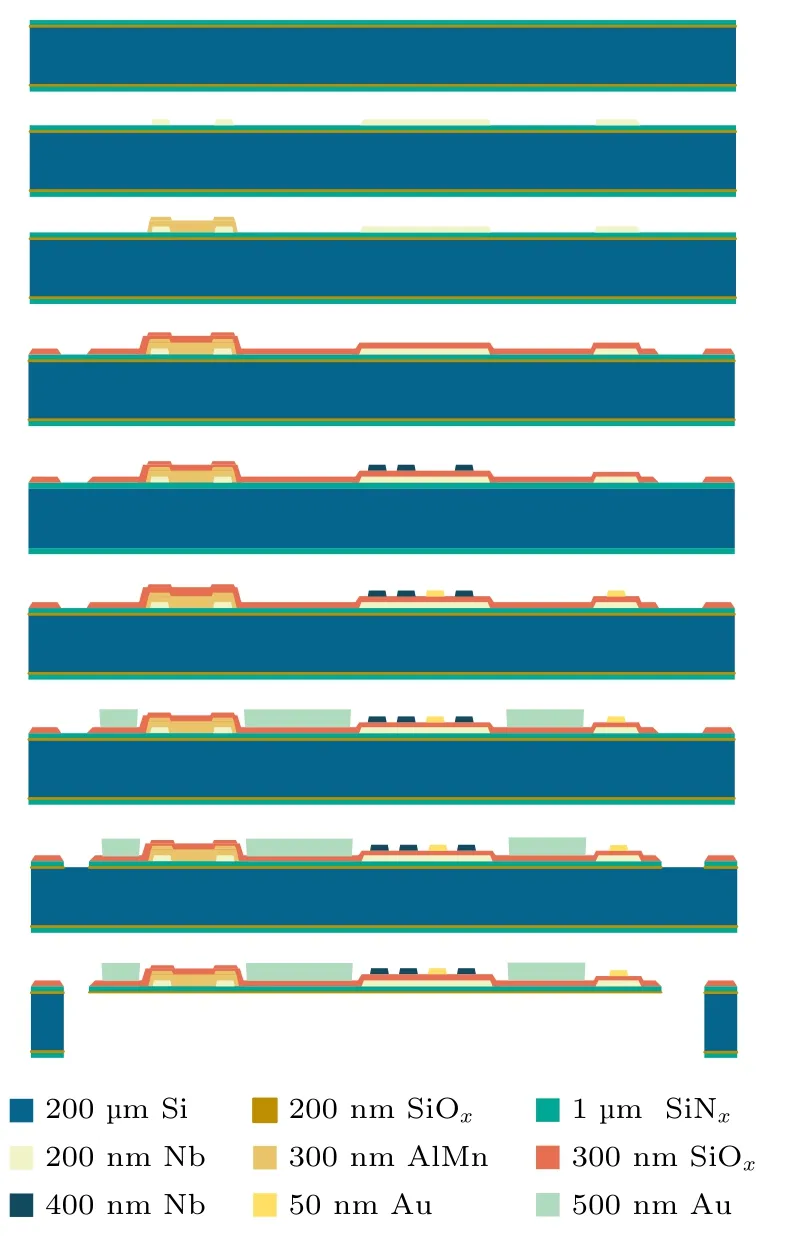
图5 TES 探测器加工过程横截面示意图Fig.5.Schematic diagram of cross-section of TES detector fabricating process.
芯片基底为200 μm 厚的100 晶向硅片,双面通过低压化学沉积(low pressure chemical vapor deposition,LPCVD)的方法分别生长200 nm 厚的氧化硅与1 μm 厚的氮化硅.为了保证与TES探测器同在一块芯片上的微波器件的性能,正面光刻步骤均使用了NIKON-I12 步进式光刻机,其标称精度为0.35 μm,实测各层精度(刻蚀后)优于0.5 μm .最下层铌层由磁控溅射的方法生长,并通过感应等离子体刻蚀(inductive coupled plasma etch,ICP)方法刻蚀以减少过刻蚀厚度.铝锰合金层通过磁控溅射的方法生长并通过标准铝腐蚀液进行腐蚀以减少干法刻蚀带来的离子污染.氧化硅介质层生长温度为75 ℃,单层应力小于200 MPa.上层铌层采用与下层相同的工艺加工.两层金层由电子束蒸发的方法进行生长并通过剥离方法成形.双面氮化硅及截止层氧化硅使用ICP 方法分别刻蚀成梁架结构与背部开窗结构.岛结构下方硅材料通过深硅刻蚀的方法进行掏空.整个加工过程梁架结构成品率超过90%.加工后芯片实物如图6(a).图中左右两侧TES 探测器连接中部微波器件进行两个极化方向信号的探测,对应梁架结构长1100 μm .上下两侧为无输入信号的盲探测器,用于观察系统稳定性等,对应TES 梁架结构长度分别为900 与700 μm .TES 探测器放大后细节如图6(b).
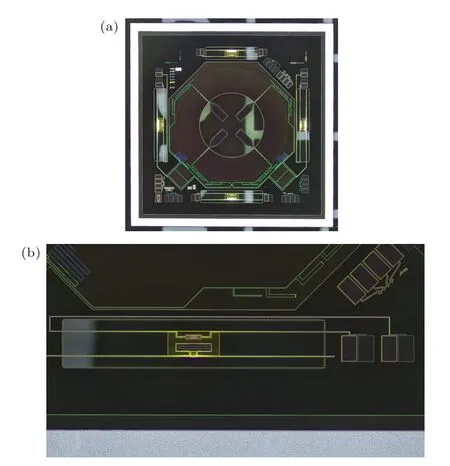
图6 (a) TES 探测器芯片整体实物照片;(b) TES 探测器局部放大照片Fig.6.(a) Overall physical photo of TES detector chip;(b) partially enlarged photo of TES detector.
为了测试TES 样品的真实性能,搭建了具有如图2 所示功能的TES 探测器工作电路.低温环境由HPD 公司生产的绝热去磁制冷机提供(图7(a)),其可提供大范围控温条件,测试过程中PID 控温精度优于30 µK.TES 样品通过图7(b)所示的样品托与制冷机相连,实测中外部加装铌制磁屏蔽罩以防止地磁干扰.样品托内PCB 板表面镀有高纯度锡层,实测寄生电阻<1µΩ .外部放大电路选用Magnicon 公司生产的两级SQUID 放大器,放大倍数标定后为 2.363×10−2V/µA .图7(b)所示的样品托上两块偏置电阻经锁相放大器以四端法进行标定,电阻值分别为 0.170与 0.165 mΩ,在工作温区内因温度产生的漂移小于0.5%.系统偏置电流由Stanford Research Systems 公司生产的CS580型电流源提供,通过6级RLC 滤波后输入.测试过程中整个芯片无外界微波信号输入,所有线缆外部均进行电磁屏蔽.

图7 (a)绝热去磁制冷机照片;(b)装载TES 的样品托的照片;(c)样品托在制冷机内安装状态的照片Fig.7.(a) Adiabatic demagnetization refrigerator;(b) sample holder loaded with TES;(c) sample holder installed in the refrigerator.
测试中3 个不同梁架长度的TES 探测器来自于同一块芯片.通过在不同的热沉温度下改变偏置电流I偏置并测量流过TES 的电流,可以计算得到不同热沉温度下TES 探测器发热功率与偏置电压的关系,如图8 (图中数据隐去了测试尾端电流过大超过SQUID 量程的部分)所示.测试中偏置电流输入范围为0—10 mA,步进长度为10 µA .绘图数据取自相同条件下1000 组测量数据的平均值,整体相对误差小于1.5%.每条曲线中部正方形实心点处对应的TES 电阻为 1/2Rn.由于测试点众多且误差较小,为方便观察,图8 没有绘出误差棒.从图8 可以看出,TES 发热功率随着偏置电压降低而降低,直到达成电热负反馈条件后开始趋于稳定.由于3 个TES 探测的超导薄膜尺寸完全相同,所以其常态电阻Rn几乎相等,约为13.4 m Ω .取不同温度下电阻为 1/2Rn时的功率为对应的饱和功率,可得到饱和功率随温度变化.将其与预测值一同绘制的曲线如图9 所示.
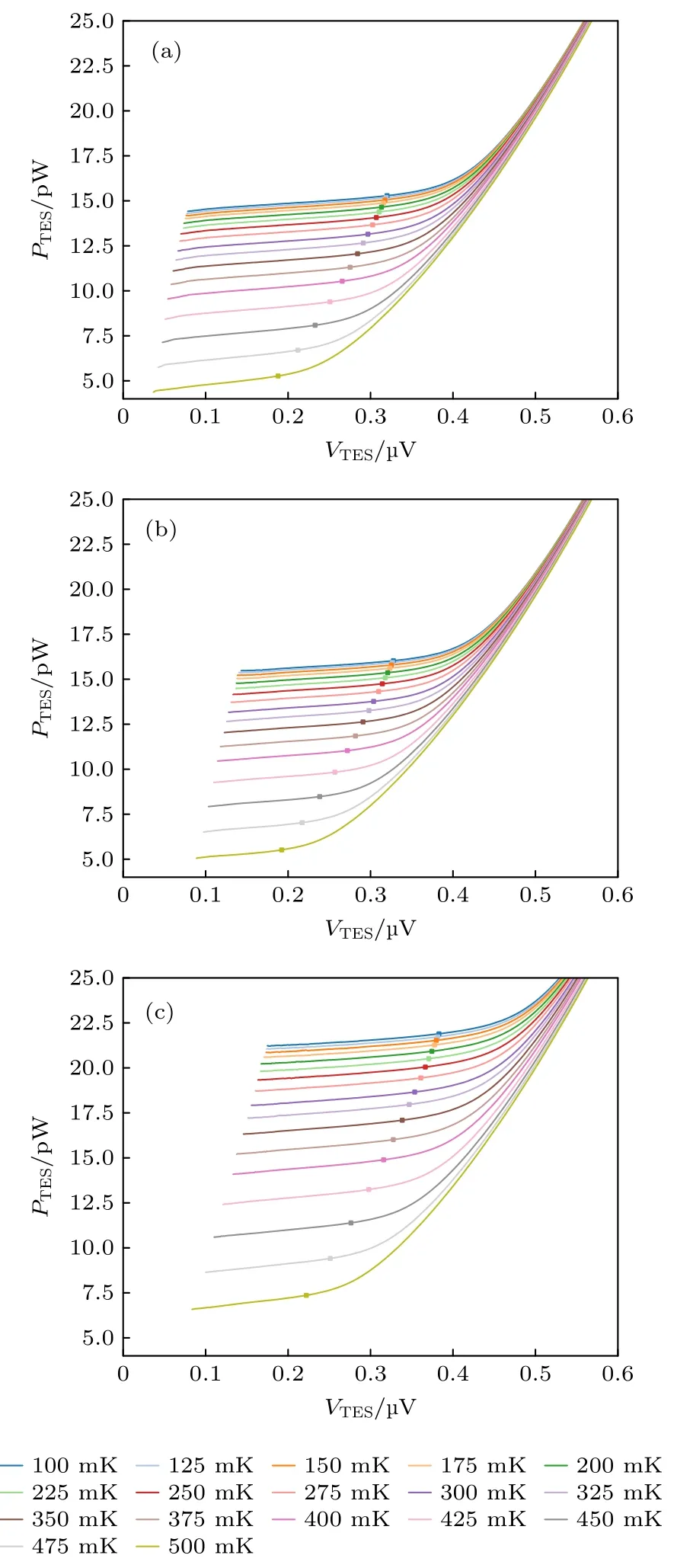
图8 不同尺寸TES 探测器发热功率 PTES 随热沉温度变化曲线 (a)样品梁架长度为1100 μm ;(b)样品梁架长度为900 μm;(c)样品梁架长度为700 μm .Fig.8.Curves of heating power as a function of heat sink temperature with different beam sizes:(a) The length of beams is 1100 µm;(b) the length of beams is 900 µm;(c) the length of beams is 700 µm.
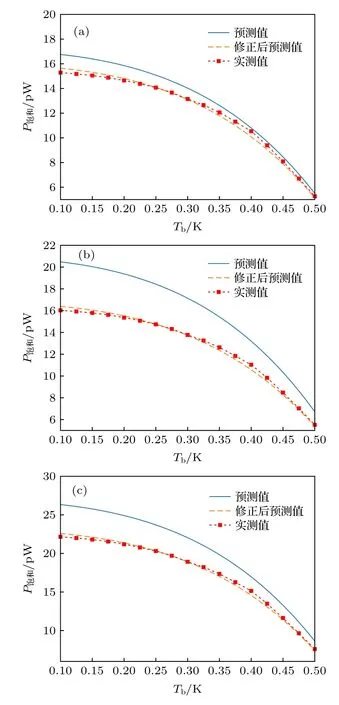
图9 不同尺寸下TES 探测器饱和功率 P饱和 随热沉温度变化曲线 (a) 样品梁架长度为1100 μm ;(b)样品梁架长度为900 μm;(c)样品梁架长度为700μmFig.9.Curve of saturation power of TES detector with heat sink temperature under different sizes:(a) The length of beams is 1100 µm;(b) the length of beams is 900 µm;(c) the length of beams is 700 µm.
由图9 中数据可知,在热沉温度为250 mK 时,梁架长度为1100 μm 的TES 探测器实测饱和功率P饱和约为13.9 pW.通过边界限制的声子输运模型计算得到的梁架尺寸与真实需求尺寸已经非常接近.观察图10(a)可知,实测值与预测值之比随温度变化趋势接近一致,但同温度下比值存在差异.参考热导率公式(7)和(18)可知,其中只有比热容C(T)为温度的函数,l有效不随温度变化.故当C(T)发生变化,会导致图10(a)中曲线形状发生变化.考虑到3 个TES 样品来自于同一个芯片,在晶圆上相隔较近.主要导热结构的成分及厚度差异应当较小,材料的比热容差异也应较小.故可以假设不同样品预测值与实际值之间比值的差异主要来自于l有效因工艺产生的散布,而三者比热容近似相同.保持比热容参数a与b不变,将3 组实测数据分别代入(15)式,使用数值方法拟合l有效所对应的f,得到修正后的f分别为0.671,0.779,0.730.使用修正后f得到的饱和功率预测值随温度变化的曲线如图9 中橙色虚线所示.实测饱和功率与修正后预测饱和功率之比随热沉温度的变化如图10(b).可以看出,3 个样品的实测饱和功率与修正后预测饱和功率之比的曲线几乎完全重合,且值非常接近于1.由此可知,上文假设基本正确.3 个样品的比热容几乎相同,随温度的变化与(14)式描述的相比,存在微量的非线性差异.同时实测饱和功率与预测饱和功率之间比值的差异主要由样品表面粗糙度差异产生.假若真实比热容与预估比热容之比约为1,预测误差完全由表面粗糙度差异产生,则3 个样品真实的f与估计值分别相差7.2%,24.4%,17.7%.从加工工艺的角度考虑,由于本实验中的铌层溅射厚度存在约±10%的浮动,所以底层铌的过刻蚀过程会导致刻蚀区域的氮化硅表面产生粗糙度变化.此应为氮化硅表面粗糙度差异的来源.
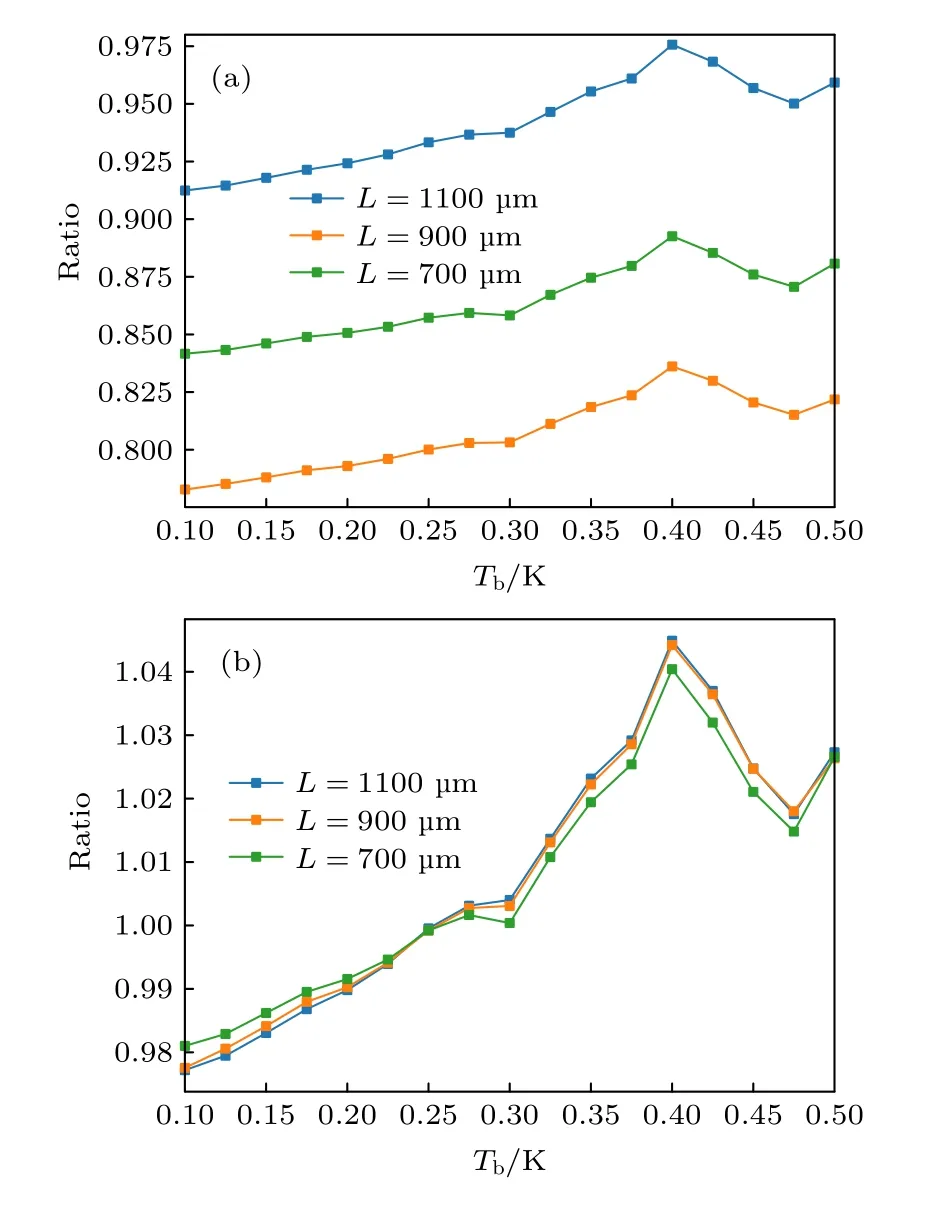
图10 (a)不同尺寸TES 探测器实际饱和功率与预测饱和功率之比随热沉温度的变化;(b)不同尺寸TES 探测器实际饱和功率与修正后预测饱和功率之比随热沉温度的变化Fig.10.(a) Ratio of actual saturation power to predicted saturation power for TES detectors of different sizes as a function of heat sink temperature;(b) the ratio of the actual saturation power to the corrected predicted saturation power of TES detectors with different sizes as a function of heat sink temperature.
5 结论
对于用于CMB 观测的TES 探测器,其探测器饱和功率目标值由观测条件决定.为实现高精度观测,探测器实际饱和功率需与目标值高度匹配.
本文以边界限制的声子输运模型为核心,通过对已有探测器参数进行拟合得到了相应模型参数,并根据目标饱和功率实现了对探测器实际物理尺寸的预估.在加工工艺上,首次在国内制备出了用于探测CMB 极化信号的TES 探测器芯片,并搭建了一整套完整的测试系统用于测试.通过将探测器实测饱和功率与预测值相比可知,本文中的声子输运模型可以比较好地对TES 探测器梁架结构尺寸进行估计.根据理论分析得到,实测数据与预测数据之间的差距主要来自于加工过程中厚度误差带来的表面粗糙度变化.
中国科学院高能物理研究所刘聪展研究员、李正伟研究员、张翼飞副研究员,中国计量科学研究院高鹤博士,加州理工学院舒诗博博士均在本文的工作中给予了有益讨论和指导,在此一并表示感谢.

