基于高频数据构建上海原油期货的量价关系模型

陈 彪，陈佳洛，吕子越，王 迪，周宇洋，赵永红

(1.四川大学 数学学院，四川 成都 610065;2.四川大学 经济学院，四川 成都 610065)

1 引言

石油作为一种重要的能源以及基础型产品，参与到人类生活的方方面面，是当今世界举足轻重、不可或缺的战略物资，被誉为“黑色的金子”，参与全球原油贸易定价体系对我国国家发展是至关重要的。于2018年3月26日在上交所正式挂牌交易的上海原油期货弥补了国际原油定价体系的缺口，增强中国和亚太地区的原油定价话语权。

在期货市场上，成交量、持仓量、期货价格波动是反映市场变化的三个重要指标，是市场参与者和监管者最为关注的数据。通过研究价格波动和成交量、持仓量之间的关系，有助于增强对期货市场内部结构和信息传播方式的了解，更好地帮助市场参与者进行投资和风险管理，并为市场监管、投资分析、政策制定提供指导。

基于量价关系的重要意义，金融市场上成交量、持仓量与价格波动的关系受到国内外学者的广泛关注。早在1973年，Clark对棉花期货的市场价格波动和成交量之间的联系进行了实证研究，首次提出混合分布假说(MDH)，将成交量作为信息到达的代理变量。随后Epps和Cornel等也通过实证研究发现成交量和价格波动之间具有正相关关系。考虑到持仓量反映的是投资者对市场走势的判断，Bessembinder和Seguin较早地将持仓量纳入研究范围，发现持仓量和价格波动呈现负相关关系。国内学术界对期货市场的研究起步较晚，多基于Clark的混合分布假说理论下的量价关系以及因果检验。叶舟等全方位探究了中国铜铝期货市场交易量和收益率及其波动的关系。戴毓、李志斌、白东辉等分别探究了我国燃料油期货市场、大豆类期货市场、铜铝期货市场中成交量、持仓量与波动性的关系。近些年计算机在金融交易领域的应用使高频数据的应用得到推广，更多的学者利用高频数据对股票市场和期货市场的量价关系特征进行了研究。Avramov等研究发现利用已实现波动率估计实际波动率能为高频数据带来更稳健的效果。但国内基于高频数据的量价关系研究大多集中于股票市场，原油期货方面相关文献较少，有很大研究空间。

在期货价格预测方面，除了传统计量的时间序列预测方法外，BP神经网络也得到了广泛运用。胡纯探讨了在期货价格的趋势预测中应用BP神经网络的可行性以及实验结果，发现BP神经网络预测精度较高，能为期货价格的预测提供依据。李婷婷在假定外围市场环境比较稳定的情况下，运用模糊BP神经网络建立了中石化股票的价格预测模型，预测效果良好。许兴军，颜钢锋基于BP神经网络对浦发银行近一年的交易数据进行了训练和学习，并发现当股价处于上升期或者下降期时预测能得到良好结果。王海军，金涛等人在BP神经网络的基础上，优化调整了网络结构和网络参数，提出了基于GRA-CS-BP算法的期货价格预测方法，仿真结果表明新方法比单纯BP神经网络模型具有更高的预测精度，具有较高的参考价值。

文章利用上海原油期货高频数据，建立了基于成交量、持仓量与已实现波动率的ARIMA模型，考虑了各变量之间的交叉影响，进一步提出了BP神经网络非线性预测模型并进行了实证分析，为期货市场的价格及走势提供参考。

2 模型构建

2.1 已实现波动率

已实现波动率的概念由Andersen和Bollerselev首先提出，具有可靠的理论依据。因其不受模型形式限制、操作简单、无参数且能更好度量真实波动率的优势,成为文章研究上海原油期货价格波动时的更优选择。

在每日的期货交易时段中平均选取M个观察时间点,并定义已实现波动率为日内高频收益平方之和，即：

其中代表特定时段的收益率，角标代表交易日，角标代表时间段。但由于上海原油期货停盘期间数据的缺失,期间的价格波动无法反映,故参考Hansen和Lunde的思路,利用尺度参数变换已实现波动率,使全天实际波动率能被更好地刻画。优化后第天已实现波动率定义为：

其中尺度参数：

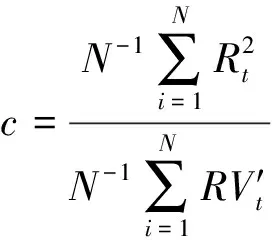
2.2 量价关系基础线性模型

首先构建以下四个线性模型分别模拟日盘和夜盘中成交量、持仓量及其相对增量对已实现波动率的影响：

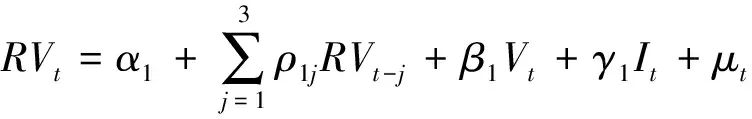
(1)

(2)

(3)

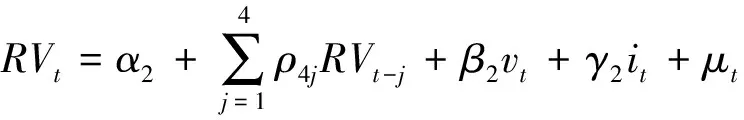
(4)

其中为前面定义的已实现波动率。和分别表示第个交易日上海原油期货的对数形式的成交量和持仓量。和分别是上海原油期货第个交易日上海原油期货的成交相对增量和持仓相对增量,其定义分别为：=100×(--1),=100×(--1)。为了消除时间序列下容易出现强自相关性，文章利用Eviews单位根检验法结合AIC和SC准则，确定出在日盘和夜盘数据下价格波动关于成交量和持仓量、成交相对增量和持仓相对增量的滞后阶数分别为3和4，并由此建立日盘模型(1)、(3)和夜盘模型(2)、(4)。

2.3 BP神经网络构建非线性模型

本研究采用人工神经网络(Artificial Neural Network,ANN)中运用最广泛的反向传播人工神经网络(简称BPNN)对上海原油期货量价关系非线性模型问题进行研究。

基于线性回归模型的结果，认为成交量、持仓量对原油期货已实现波动率的影响与成交相对增量、持仓相对增量对该问题的影响具有基本相同的规律，故在做BPNN的非线性模型时，仅考虑成交相对增量、持仓相对增量对本研究问题的影响效应。同时，在线性模型基础上，进一步提出将相对成交增量、相对持仓增量分为预期与非预期两部分(考虑到外来信息会引起期货市场价格的波动，而未来的信息是无法预期的，所以预期到的成交量和非预期成交量对价格波动的影响是不同的，对持仓量同样如此)。因此为了更进一步探究上海原油期货市场价格波动与成交量、持仓量各部分之间的关系，借鉴Bessembinder和Seguin的研究成果，将成交量和持仓量分别分解为可预期部分和非可预期部分，探究预期成交量和非预期成交量以及预期持仓量和非预期持仓量对价格波动的不同影响。为了消除成交量和持仓量的序列自相关，利用自回归移动平均模型ARIMA(，)对成交量和持仓量进行回归：

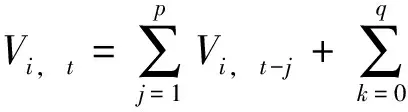
(5)

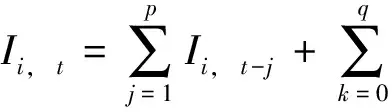
(6)

其中预期部分为通过ARIMA(，)模型计算出的拟合值，非预期部分是其实际值与拟合值之差。ARIMA模型中滞后项的选择基于AIC准则和SC准则，确定最合适的和值。经比较分析，对日盘成交量选择 ARMA(7，0)模型，对日盘持仓量选择 ARMA (1，1)模型。

BP算法原理。BP算法是常用的机器学习的核心算法，其信息处理单元是神经元，神经元的输出信息是来自上一级神经元的输入信息的加权和，是信息整合的过程。一旦整合后的信息超过该神经元的阈值水平，该神经元就被激活，并通过转移函数，可输出非线性信息。BPNN通常包括输入层(P层)、隐藏层(H层)和输出层(T层)，其中H层无法直接进行观察，可以根据需要设计为多层。BP神经网络包括输入信号的正向传递和误差信号的反向传递。

输入信号的正向传递过程由输入信号的加权求和与转移输出组成，其中P层与H层间、H层与T层间分别以输入神经元的权重、输出神经元的偏置以及激活函数Sigmoid函数连接，在网络中信息以非线性形式传递。定义和分别为下一层神经元的输入和输出值，为来自上一层神经元的信号输入值，为上一层到下一层的权重，为下一层神经元的阈值或偏置值，转移函数()为Sigmoid函数。其大体运作原理如下：

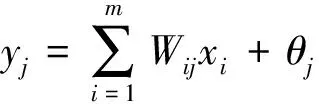
(7)

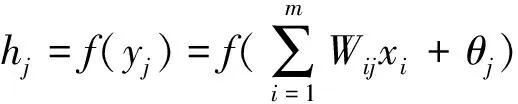
(8)

(9)

误差信号的反向传播是指将输出层的实际输出值与期望输出值做比较，若有误差，则将误差信号反方向逐层传导，将误差看作关于权值和阈值的函数，借助梯度下降算法，通过按梯度的负方向调整权值和阈值，经多次迭代，使误差最小化。

与传统的回归分析相比，BP神经网络增加了隐层，有助于更精准地模拟现实生活中复杂的非线性关系。BP神经网络也是目前应用最为广泛的神经网络，在期货预测中的应用有重要参考价值，具有精度高、泛化性能好等优点。基于BP算法的前馈网络可以以任意精度逼近任何非线性函数，对短期价格预测效果良好。因此，仍利用上述数据采用BP神经网络对原油期货的价格进行非线性拟合与预测。

3 实证分析

3.1 数据和基本统计量分析

文章选取上海原油期货2018年3月27日至2019年12月30日的成交量、持仓量、收盘价的分钟级数据,剔除节假日和缺乏夜盘的交易日,共计419个交易日数据,每日上午及下午的交易时间归为日盘数据,共计225个时间间隔；每日夜晚及次日凌晨的交易时间归为夜盘数据,共计330个时间间隔。同时考虑到日盘和夜盘的数据数量以及交易者活跃性的差异,选择将其分别建模。根据前文模型建立中变量的定义,分别计算出有效日期的日盘与夜盘的日对数成交量、日对数持仓量以及日成交相对增量、日持仓相对增量和已实现波动率。

考虑到数据中可能存在对模型影响较大的异常值点,文章通过计算学生化外残差并结合“3σ原则”去除离群点,后利用SPSS软件计算出各数据的杠杆值以及库克距离,指标数据均在正常值内，可以认为处理后的数据不具有强影响点，且具有平稳性。

3.2 线性回归过程讨论及结果

对模型自变量分别进行D-W检验和共线性诊断,确定数据不存在一阶自相关性和多重共线性,从而建立模型时回归系数具有统计学意义,奠定了量价关系模型的统计基础。但在利用Eviews进行White检验过程中发现R-squared数据的p值 Prob.Chi-Square均小于0.05,具有异方差性。此时用传统的最小二乘法估计模型,得到的参数估计量不是有效估计量,也不是渐进有效的估计量,无法对模型参数进行有关显著性检验。故文章采用统计学中对存在异方差性的模型常用的加权最小二乘法进行模型构建。利用加权线性回归得到上海原油期货日盘与夜盘中量价关系线性模型，如表1所示。

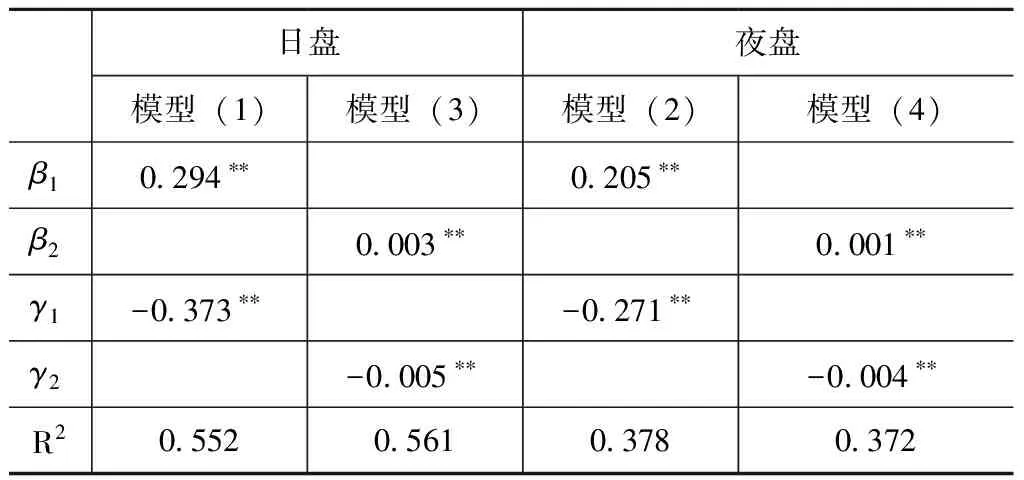
表1 上海原油期货量价关系基础模型的估计结果

研究结果表明,量价关系规律在日盘与夜盘中相同。首先分析模型(1)、(2):系数在5%显著性水平下显著为正，说明对数成交量和已实现波动率有同向变化的趋势,即成交量的增长会导致上海原油期货的价格波动加大。系数在5%显著性水平下显著为负,说明对数持仓量和已实现波动率有反向变化的趋势,即持仓量的增加会导致上海原油期货的价格波动减缓。而对反映原油期货市场价格波动与成交相对增量、持仓相对增量关系的模型(3)、(4)，与模型(1)和(2)相比，显著性水平和系数的正负均相似,故分析结果也相似，体现为成交量变化幅度的原油期货价格波动幅度呈现同向变化趋势,而持仓量变化幅度则与价格波动的变化呈现反向变化趋势。

3.3 非线性模型估计过程及结果

通过以下四个步骤构建关于上海原油期货的BP神经网络非线性模型:第一,模型构建,根据研究目标与经验公式分别确定P、H和T层的神经元数和学习速率等模型参数;第二,训练模型与测试,将样本数据分为训练组(train)、验证组(validation)和测试组(test)三个组别,通过训练组和验证组的训练,找到拟合效果最好的非线性模型;第三,仿真测试,将测试组中的输入项(Input)输入模型,随后对比模型的仿真输出值与目标值,并根据相关指标判断模型精准度以及误差大小与所定义的正确率;第四,权重估计,即计算该模型各输入项的权重,结合有关信息综合判断成交量与持仓量对上海原油期货已实现波动率的影响效应。

3.3.1 非线性模型构建过程

根据日盘与夜盘的数据建立两个BP神经网络模型。说明如下:

第一,输入层与输出层的设计见表2。日盘模型已实现波动率滞后阶为3阶,夜盘滞后阶为4阶。所以可设日盘P层有七个神经元,夜盘P层有八个神经元。日盘与夜盘的T层都为一个神经元:上海原油期货已实现波动率。关于H层的设计,则根据常用的经验公式确定H层有两层,其中日盘的H层分别为20和3个神经元,夜盘的H层则分别为15和8个神经元。

表2 BP输入层和输出层对应指标

第二，激活函数选择。本研究选择最经典的Sigmoid函数。

第三,训练集、验证集以及测试集的划分。训练集依照MATLAB help中参考资料选定原数据集的70%,验证集选定15%的数据,因为算法产生的随机性,需要验证集合不断调试出较优的模型。同样地,测试集选定15%,用于比较经过筛选后的网络所预测出的值与真实值的差距,以产生的MSE、R以及所定义的正确率来评判模型好坏。文章中提出正确率的定义如下: 正确率是两个时间单位间数据仿真值与数据期望值的差值正负相同的数据所占比例。

第四,权重计算与判断。根据上述步骤获得指标较好的BP模型后,提取P层到H层的权重共720个,再通过以下公式分别计算输入层各项神经元信号值的权重,从列矩阵读出结果。其中，代表神经元信号值的权重，以此来分析各影响因素对已实现波动率的影响。

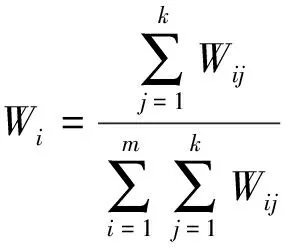
3.3.2 非线性模型结果

建立并使用训练组数据训练出较好神经网络模型。根据成交相对增量的预期部分、非预期部分和持仓相对增量的预期、非预期部分以及滞后的三阶或四阶,分别采用日盘与夜盘的训练后模型,仿真日盘与夜盘的已实现波动率。得到训练组的样本仿真值与目标值拥有相似的总体变化趋势,如图1和图2所示。

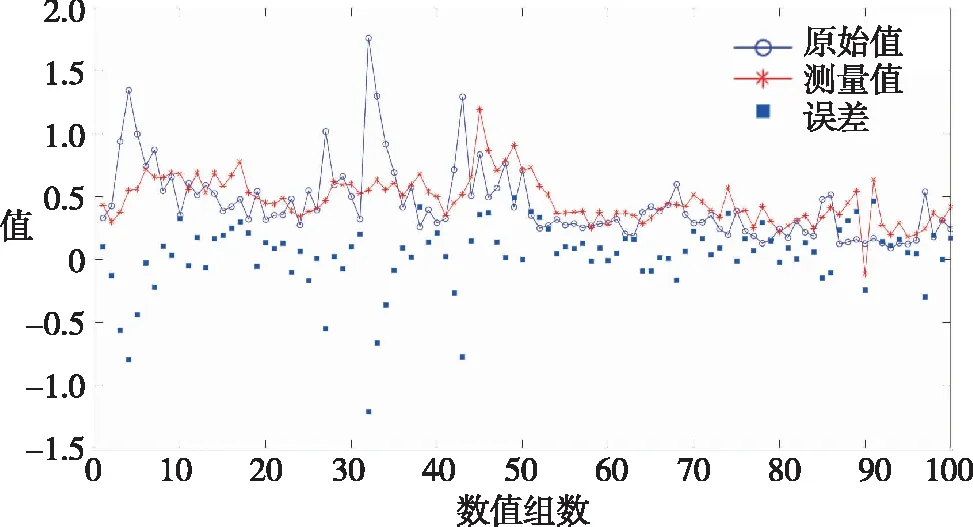
图1 日盘BP模型训练结果

图2 夜盘BP模型训练结果

图1～图2显示,训练后的模型能够在一定标准上拟合已实现波动率目标值变化趋势，亦体现了训练样本的基本特点。

通常应根据实际需要评估模型的精确度与好坏,各行业具体标准不一。如在生产领域,有的文献对比模型的仿真计算值与产品标准件实际测量值的平均值,并依据一定的置信区间(如95%的置信区间),评估总体均值与抽样误差后进而判断仿真结果的达标率。而对于文章的研究,由于为大样本时间序列数据,且研究对象为上海原油期货,仍受新冠肺炎疫情的影响,故模型构建重点侧重于成交量、持仓量对原油期货价格波动的影响以及通过该模型对原油期货价格变化趋势的预测。所以文章通过模型的R值、MSE值以及提出的正确率三个指标进行判定。其中,数据R代表该模型的输出与目标之间的相关性,MSE为均方误差,正确率则大致刻画了大体趋势的准确程度。

将经过训练和验证之后的模型用于测试组,最后获得日盘和夜盘中两个模型用于训练集、验证集、测试集以及所有样本数据的拟合效果结果R、MSE以及正确率,见表3。日盘四个集合的R都大于0.6,夜盘的R都大于0.5,故认为该模型的R结果已相对理想。

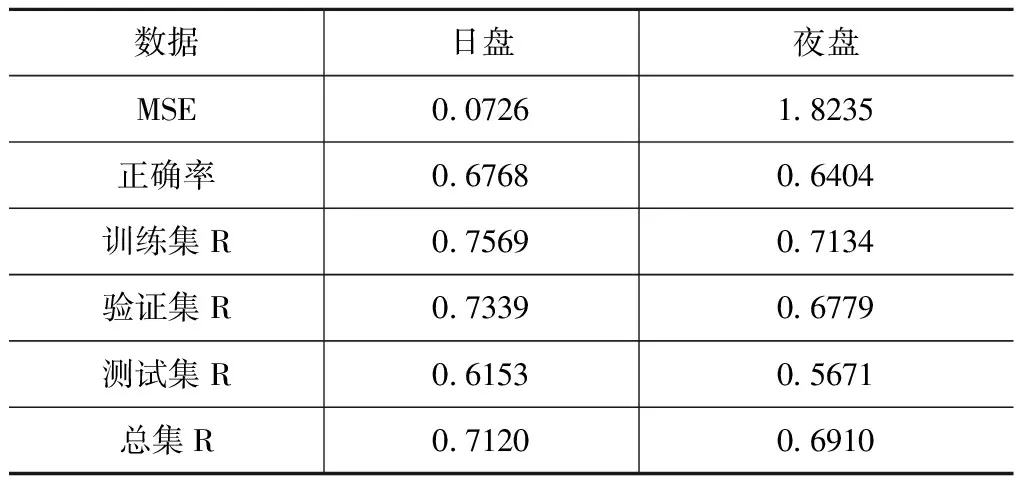
表3 BP模型正确率及MSE

得到较为理想的BP模型后,根据模型数据分别计算出输入层各神经元信号值的权重W矩阵,数据如表4所示。指标的权重一定程度上说明了该指标的相对重要性与影响的大小(评价学原理)，故W矩阵显示了输入神经元信号值影响效应的相对大小。

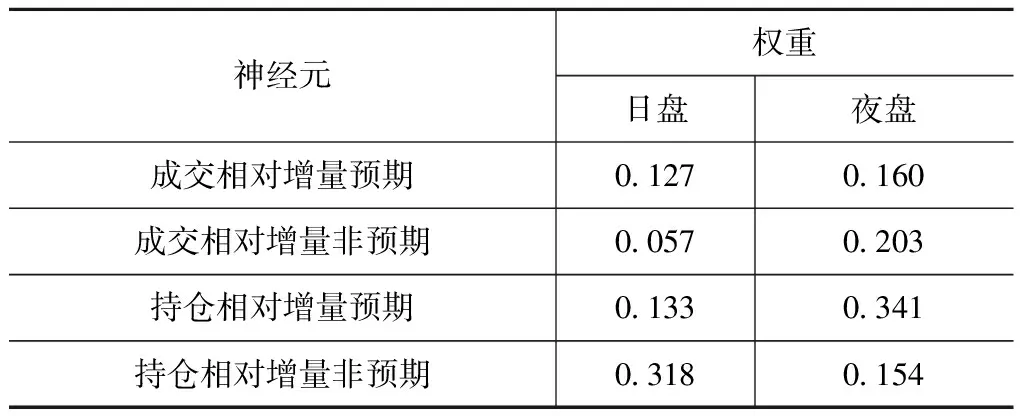
表4 BP输入层各神经元权重

在日盘模型中,按照影响效应大小排序,依次是持仓相对增量非预期部分、持仓相对增量预期部分、成交相对增量预期部分、成交相对增量非预期部分。该结果一定程度上表明持仓量对日盘价格波动具有较大影响,且非预期部分相较预期部分影响更大;夜盘的影响效应从大到小依次是持仓相对增量预期部分、成交相对增量非预期部分、成交相对增量预期部分、持仓相对增量非预期部分。表明了夜盘成交量中,非预期部分对价格波动的影响更大,而夜盘的持仓量结果与日盘相反。

参考朱学红认为非预期持仓量(成交量)代表投资者未来的信息,具有无法预料性,这些意料外的信息会引发期货市场的价格波动。所以预期与非预期部分对价格波动的影响是很不同的,且一般来说非预期部分易造成更大影响,实证结果也诠释了日盘中持仓量非预期部分影响更大,夜盘中成交量非预期部分亦影响更强。另外,期货市场中知情交易者的比例可通过预期成交量(持仓量)显示出,流动性交易者的比例则由非预期成交量(持仓量)反映,故该结果可表明,上海原油期货市场中流动性交易者占比较大,契合市场流动性理论。

4 结语

文章采用以一分钟为采集频率的高频数据,探究上海原油期货市场中的量价关系问题:在日盘、夜盘中成交量、持仓量对价格波动分别具有哪些影响。基于诸多国内外学者的研究分析,文章将交易日的日盘和夜盘数据分离分别建模,采用已实现波动率作为价格波动的有效度量,探究成交量、成交相对增量、持仓量、持仓相对增量对价格波动的影响。线性回归结果表明,成交量对价格波动的影响表现为正向,即成交量增多价格上涨;持仓量对价格波动的影响与成交量相反,表现为负向影响,即持仓量增多价格反而会下跌;成交相对增量和持仓相对增量对价格波动的影响也分别体现为显著的正相关和负相关关系。

在线性回归的基础上,进一步细化解释变量即成交量、持仓量,利用成交相对增量的预期、非预期部分与持仓相对增量的预期、非预期部分持仓相对增量、已实现波动率的数据,进一步运用BP神经网络构建非线性量价关系模型,获得了更为准确的模型结果。其训练权重信息补充了线性回归结果:日盘与夜盘的价格波动影响因素具有一定差别,持仓量的非预期部分对日盘价格波动影响最大;而持仓量的预期部分对夜盘价格波动影响最大。在构建的日盘模型中,持仓量非预期部分对价格波动的影响大于持仓量预期部分;而在夜盘模型中,对价格波动的影响为成交量的非预期部分大于预期部分。

文章实证所得的上海原油期货市场中成交量、持仓量对价格波动的影响以及日盘与夜盘差异化、非预期部分与预期部分的不同影响等结果,一定程度上有助于投资者判定其市场走势、价格变化,从而合理地进行投资和规避风险。同时也为该期货市场的监管者提供了有效信息,保证市场合理运作。