基于PFC数值模拟的土石混合体剪切特性研究

谷 东 京，李 建 林，黄 宜 胜

(三峡大学 水利与环境学院，湖北 宜昌 443002)

0 引 言

土石混合体主要是由土体和岩体组成，是一类介于土体和岩体之间的特殊地质体[1-3]。土石混合体在中国分布广泛，长江上游内90%为土石混合体滑坡[4-8]。由于土石混合体力学性能不稳定，会对工程建设造成很大的困难。但土石混合体也是一种被广泛运用的工程地质材料[4]，在工程施工中经常使用。因此，研究土石混合体的破坏机理及其力学性能，对开展土石混合体工程建设及防灾减灾具有重要意义。

土石混合体的力学性质十分复杂，影响因素较多。为此，许多学者通过现场原位试验、室内试验和数值试验进行了深入研究[9-12]，主要是研究块石的含量、块石的形状以及块石在剪切过程中的位置等因素对土石混合体剪切强度的影响。例如，李晓[13]、油新华[14]等在三峡库区白衣庵滑坡现场进行了原位推剪试验和压剪试验，获得了土石混合体的应力-应变曲线。欧阳振华等[15]通过对土石混合体中块石的力学性能的研究，得出了块石的粒径对土石混合体的力学性能影响最大，含石量的多少则次之的结论。丁秀丽等[16]运用PFC方法来模拟土石混合体的双轴压缩试验，结果发现土石混合体的应力-应变关系呈台阶状分布。贾学明等[17]运用PFC3D软件模拟500 mm×500 mm×400 mm尺寸的土石混合体剪切试验，结果发现：含石量为60%～80%的土石混合体剪切面起伏度最大达到了6.0 cm，含石量为20%～60%时，最大起伏度达到了5.2 cm。宋岳等[18]通过土石混合体剪切强度试验，发现内摩擦角随着试验高程的降低而减小，黏聚力随着高程的降低而变大。黄宜胜等[19]通过开展土石混合体剪切强度室内外对比试验，发现土石混合体在剪切过程中表现出了应力屈服及塑性变形，说明土石混合体这种材料具有较高的承载能力和大变形特征。

本文基于室内原状样直剪试验，并运用PFC2D软件，研究了土石混合体模型不同颗粒级配组粒径质量分数与颗粒的缺失对剪切强度的影响，以及不同颗粒级配组粒径质量分数模型的5组尺寸对剪切强度的影响。

1 室内原状样直剪试验方案

1.1 采样地点

室内试验试样取自于重庆市奉节县的三峡库区藕塘滑坡体，现场采样点如图1所示[20]。采样点的位置从低到高分别用XCZJ1、XCZJ2、XCZJ3、XCZJ4表示，每个采样点采集4个原状样。由于XCZJ1、XCZJ2、XCZJ3、XCZJ4为现场试验点编号，而本文主要是对室内试验进行研究，为了区别现场试验点，需将试验点进行重新编号。室内试验时，试验点从下到上编号为SNZJ1、SNZJ2、SNZJ3、SNZJ4。

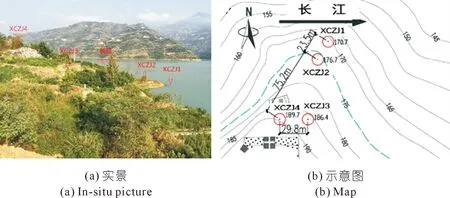
图1 藕塘滑坡及取样点位置Fig.1 Location of Outang landslide and sampling points

1.2 试验设备

本次室内试验采用YZW1000型应力式直剪仪对原状样进行直剪试验，直剪仪如图2所示。原状样形状为直径240 mm、高200 mm的圆柱体。

图2 YZW1000型应力式直剪仪Fig.2 YZW1000 stress type direct shear instrument

1.3 试验方案

对每个采样点所采集的4个原状样分别施加100，200，300 kPa和400 kPa的法向应力。将原状样放入直剪仪中，并设置剪切参数。其中，水平剪切速率为1.0 mm/min，剪切位移达到36 mm时停止剪切，剪切后的原状样如图3所示。图3分别表示SNZJ1试验点原状样在100 kPa法向应力下的剪切面；SNZJ2试验点原状样是在200 kPa法向应力下的剪切面；SNZJ3试验点原状样是在300 kPa法向应力下的剪切面；SNZJ4试验点原状样是在400 kPa法向应力下的剪切面。

1.4 颗粒级配分析

将现场试验点的试样进行室内颗粒筛分试验，得到不同高程下土石混合体各粒组的质量分数直方图，如图4所示。将室内试验测得的含水率、密度、不均匀系数以及曲率系数等列于表1。

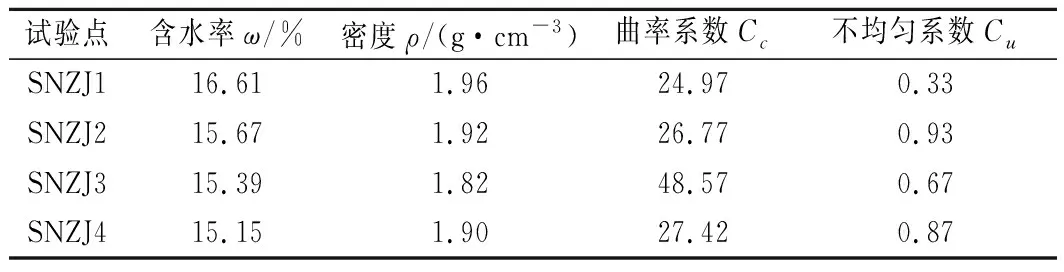
表1 含水率、密度、不均匀系数及曲率系数统计

从图4可以看出：不同高程的各粒组含量分布呈现为中间高两边低的形态，其中，2～5 mm的粒径在粒组中占有比重最大。这4个高程中，所有的粒径组大部分分布在5～10 mm的右侧，左侧只占据很少一部分，这表明该地区的土质粒径含量以小于5 mm的土颗粒为主。

从表1可以看出：试样的含水率随着试验点高程的增大而逐渐减小，试样的密度则是随着试验点高程的增大而呈现出先减小后增大的趋势。

通过对表1列出的曲率系数和不均匀系数进行分析，可以得出：藕塘滑坡各粒径分布不均，并且其离散程度较大，曲率系数均大于24。同时，从图4可以看出：2号试验点和3号试验点缺少30 mm和60 mm的粒径，说明藕塘滑坡级配不连续。综上分析，不均匀系数均小于1，说明该地区的土石混合体为级配不良的土体。

2 室内原状样试验结果分析

室内直剪试验的剪切应力-剪切位移关系曲线如图5所示。

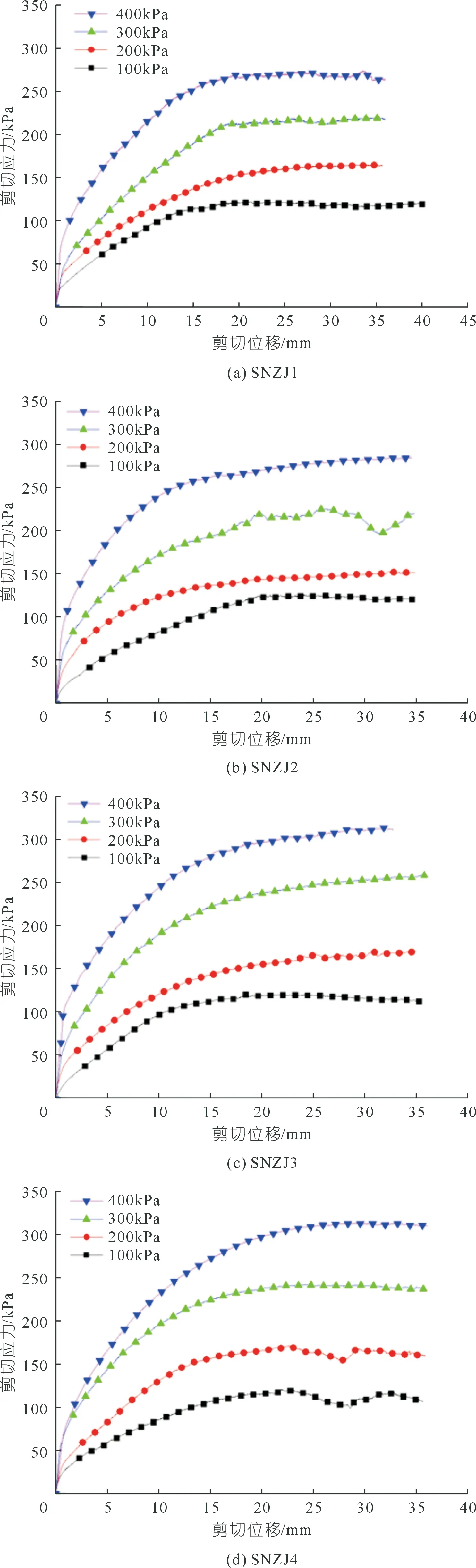
图5 室内原状样直剪试验剪切应力-剪切位移关系曲线Fig.5 Relation curve of shear stress and shear displacement in direct shear test of undisturbed samples in laboratory

从图5可以看出：室内试验原状样的剪切应力均随法向应力的增大而增大，而且所有的剪切应力-剪切位移曲线都呈现直线上升、缓慢上升和基本水平这3种形态。随着法向应力的不断增大，直线上升和缓慢上升段的剪切应力快速升高，其相应的剪切位移就会越来越小；相应的应变强化阶段中的剪切位移就会越来越大，而剪切应力在一定范围内变动，几乎呈水平状态。

同时，从图5还可以看出：① 在高法向应力(300 kPa和400 kPa)下，土石混合体的剪切应力-剪切位移关系曲线总体来说比较平滑，如图5中的SNZJ3和SNZJ4所示；② 在低法向应力(100 kPa和200 kPa)下，土石混合体的剪切应力-剪切位移曲线，总体来说出现上下波动的现象比较明显，如图5中的SNZJ2、SNZJ3、SNZJ4所示。这可能是因为在低法向应力状态下，土石混合体在剪切过程中土体与块石之间可能还存在较大的空隙。因此，剪切应力-剪切位移关系曲线出现上下波动比较明显。

3 土石混合体数值模型试验

3.1 数值模型的建立

在本次数值模拟试验中主要是采用PFC2D进行分析。模型中的颗粒生成，按照图4中SNZJ1试验点的颗粒筛分试验数据来建模。由于受到计算机运算能力的影响，所以将直径低于5 mm的颗粒统一按照5 mm的粒径来生成。在生成过程中，为了防止颗粒之间产生重叠，将颗粒采用颗粒直径放大法来进行建模，使其模型达到平衡状态。

模型尺寸为240 mm×200 mm(直径×高度)，模型共生成38 565个颗粒。其中，最小颗粒直径为5 mm，最大颗粒直径为60 mm，并将直径5 mm的颗粒设置为土体属性，密度为2 000 kg/m3，将大于5 mm的颗粒设置为块石属性，密度为2 500 kg/m3。生成的模型如图6所示(其中，红色颗粒表示块石，蓝色颗粒表示土体)。由于在实际情况中，块石的形状是不规则的，当剪切发生时，块石的不规则形状会增加其咬合力，所以本文模型块石之间的颗粒发生接触时，其摩擦系数为0.5；当土体之间的颗粒发生接触时，其摩擦系数为0.3。

图6 数值模型Fig.6 Numerical model diagram

本次数值模拟加载的法向应力为400 kPa，剪切速率为0.07 m/s，当模型的剪切位移达到36 mm时停止剪切。剪切完成的图像如图7所示。

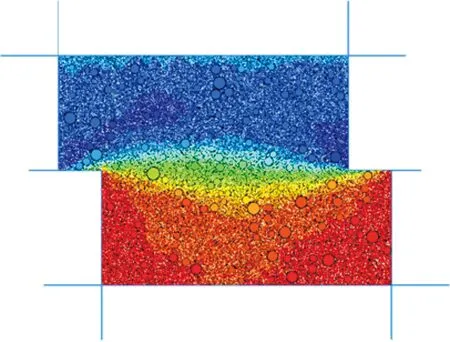
图7 剪切后模型Fig.7 Model diagram after shearing

需要指出的是，本文数值模拟剪切速率为0.07 m/s，而室内试验的剪切速率为1.0 mm/min。之所以会有如此大的差异，是因为：

(1) 本文数值模拟剪切速率如果采用室内试验的剪切速率，将需要大量的时间来完成(估计1 a多的时间)，这是因为本文数值模拟试验曲线较多，且工作量大，采用室内直剪试验的剪切速率是不现实的。

(2) 本文主要是以颗粒级配含量为研究对象，而不是研究剪切速率对抗剪强度的影响，因此，本文采用单一控制变量法将所有剪切模型都设置为0.07 m/s，这样既可以快速完成试验，试验结果又不会产生误差。

3.2 室内试验与数值模拟试验对比

本次数值模拟，是以室内试验SNZJ1(见图5(a))内4个不同法向应力下(100，200，300 kPa和400 kPa)的剪切应力-剪切位移曲线为依据而展开的。

模型剪切完成后的应力-位移曲线与室内直剪试验的应力-位移曲线如图8所示。图8表示的是不同法向应力下数值模型剪切应力-剪切位移关系曲线与室内试验模拟曲线对比图。SNZJ1-100 kPa表示以室内SNZJ1试验点为基础，室内试验与数值模拟试验在100 kPa下剪切应力-剪切位移对比图。图8(b)、图8(c)、图8(d)的命名方法与上述一致，在此不再赘述。

图8 不同法向应力下的室内试验与数值模拟试验对比Fig.8 Comparison of laboratory test and numerical simulation test under different normal stresses

从图8可以看出：数值模型在4种不同法向应力下得出的剪切应力-剪切位移关系曲线，与室内试验的剪切应力-剪切位移关系曲线重合较多，曲线趋势大致相同。由此说明，本文的数值模拟效果较好。并且由图8还可以看出：随着法向应力的不断增大，数值模拟曲线与室内试验曲线重合就会越多，误差就越小。

3.3 数值模拟结果分析

3.3.1不同颗粒级配组粒径质量分数对剪切强度的影响

为了更好地研究粒径质量分数对模型抗剪强度的影响，将室内试验SNZJ1试验点的颗粒级配按照表2的方式进行分组。表2中：试验数据一行是表示SNZJ1试验点高程的颗粒级配质量分数，并用0-0命名；1-1，1-2，1-3和1-4这4行，表示第1组模型中第1，2，3，4个模型的颗粒级配质量分数；2-1，2-2，2-3，2-4和2-5这5行，表示第2组模型中第1，2，3，4，5个模型的颗粒级配质量分数；以下分组与上述含义一样，在此不再赘述。由于表1中1-3，2-3，3-3，4-2，5-2和6-3的颗粒级配与0-0相同，所以用1-3(0-0)，2-3(0-0)，3-3(0-0)，4-2(0-0)，5-2(0-0)，6-3(0-0)表示。表2中加粗的字体为该粒径质量分数相比SNZJ1试验点的该粒径质量分数发生了改变，并将5 mm的粒径命名为细颗粒，将大于5 mm的粒径组命名为粗颗粒。

从图9可以看出：在相同法向应力的作用下，当粗颗粒的含量保持不变，只改变粗颗粒各个粒径的含量时，每组的剪切应力-剪切位移关系曲线没有发生较大的改变(如1～6组剪切应力-剪切位移关系曲线)；但是当粗颗粒的含量发生改变时，每组的剪切应力-剪切位移关系曲线发生较大的差异(如第7组剪切应力-剪切位移关系曲线)。其中，当粗颗粒中各个粒径组的含量越来越少时，所对应的剪切应力就会越来越大，也就是说在土石混合体中，细颗粒含量的大小是决定土石混合体剪切应力大小的主要因素。细颗粒的含量越大，其对应的剪切应力就会越大；细颗粒的含量越小，所对应的剪切应力就会越小。

3.3.2粒径质量分数缺失对剪切强度的影响

为了更好地研究土石混合体某一粒径缺失对整个模型剪切强度的影响，以表2中第1组第1个模型(此处命名为1-1-0)的颗粒级配为基准，先将10～20 mm的粒径质量分数去除，将缺失的部分添加到5 mm的细颗粒质量分数上，其他粒径的质量分数不发生改变，并将该组命名为1-1-1，1-1-2和1-1-3的方法如上所述，在此不再赘述。表中加粗部分为该粒径相比1-1-0组该粒径发生缺失(见表3)。

表2 不同颗粒级配组粒径质量分数

从表3和图10可以看出：细颗粒质量分数越大，所对应的剪切强度就会越大；反之，则剪切强度越小。细颗粒所含粒径的质量分数的多少对整个模型的剪切强度起到至关重要的作用。该结论与第3.3.1节部分结论相同。

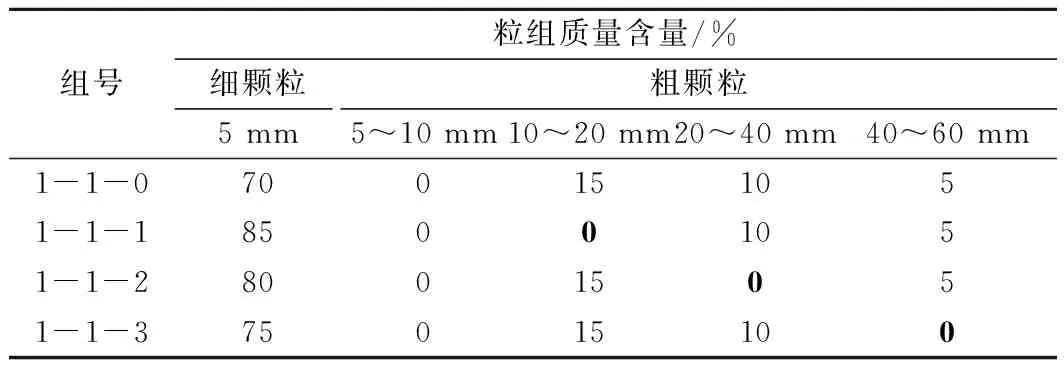
表3 1-1组缺失粒径的质量分数

从图10和图9(7组)对比可以看出：如果细颗粒的质量分数≥85%，则剪切应力-剪切位移关系曲线变化明显；反之，则剪切应力-剪切位移关系曲线变化不明显。由此可以看出，细颗粒(粒径为5 mm)的粒径质量分数85%是区分剪切应力-剪切位移关系波动明显的分界线。

图9 1～7组的剪切应力-剪切位移关系曲线Fig.9 Shear stress-shear displacement relationship curve of groups 1～7

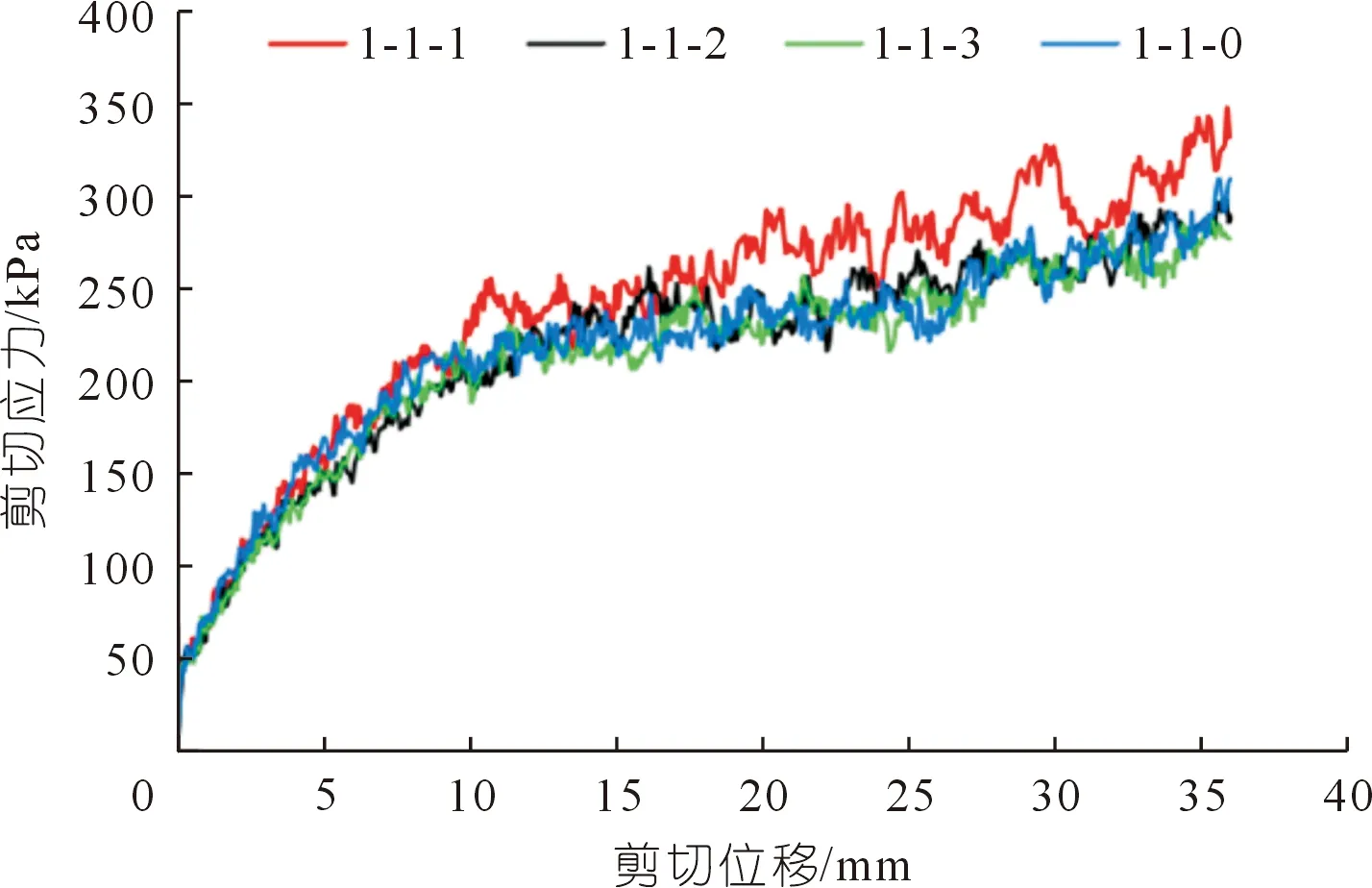
图10 1-1组剪切应力-剪切位移关系曲线Fig.10 Shear stress-shear displacement relationship curves of 1-1 group

3.3.3不同颗粒级配组的尺寸效应对剪切强度的影响

表4是分别选取表2中的1-1，3-1，7-2和7-5这4组数据来研究模型的尺寸效应。表4中的模型尺寸的长度和宽度，分别按照60 mm和50 mm的等差值进行递增。研究模型尺寸效应对模型抗剪强度的影响，主要通过二维模型的平面面积来研究。查阅文献可知：当土石混合体剪切位移达到模型总长度的15%

表4 4组模型的尺寸及其最大抗剪强度

时，剪切模型已经破坏，所以这4组模型5种尺寸的停止剪切位移分别为18，27，36，45 mm和54 mm。图11中，1-1-1，1-1-2，1-1-3，1-1-4和1-1-5是对1-1组分别按照5种尺寸进行分组的编号。其他3组编号与此相同，在此不再赘述。

从图11可以看出：随着模型剪切面积的不断增大，模型剪切应力-剪切位移曲线在不断向下移动，并且曲线增长缓慢。由此可以得出：当模型位移相同时，模型面积较小的模型，剪切应力快速增长，表现为脆性破坏；模型面积较大时，剪切应力增长缓慢，表现为塑性破坏。这也说明，面积大的模型有较大的承载力和大变形特征。

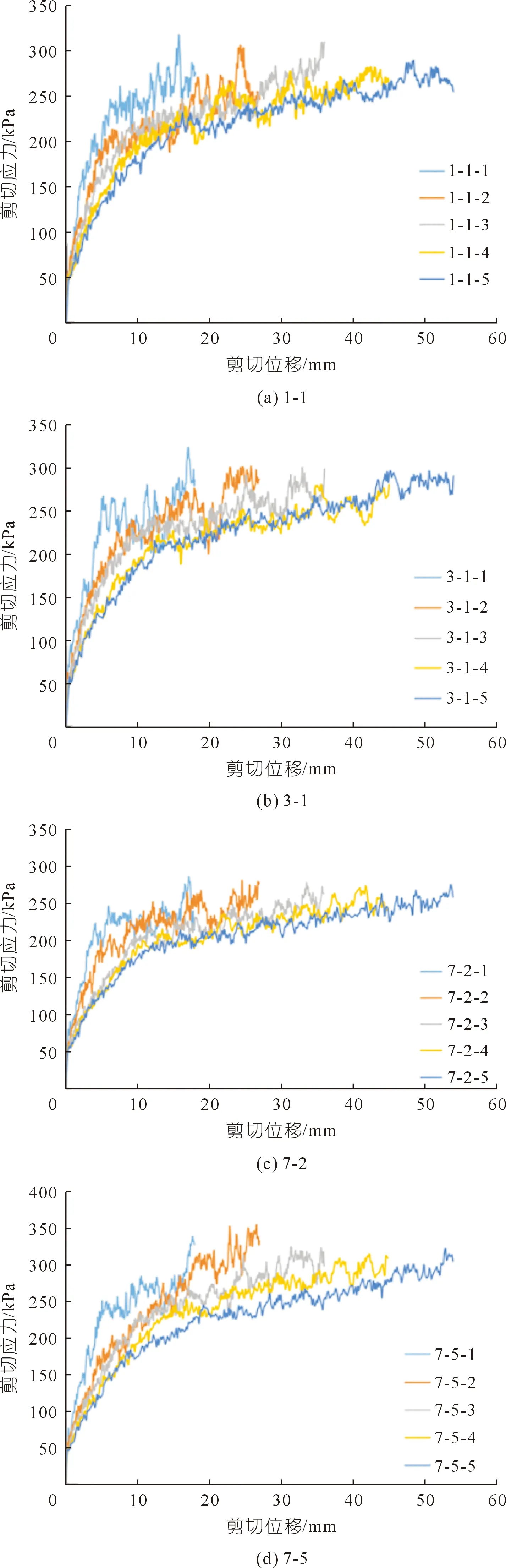
图11 4种模型尺寸的剪切应力-剪切位移关系曲线Fig.11 Shear stress-shear displacement relationship curves of four groups with different areas

为了更好地描述尺寸效应对抗剪强度的影响，将表4用图12的形式展现出来。从图12的拟合情况可以看出：模型的抗剪强度的大小总体来说随着尺寸面积的增大而不断减小。从图12(a)、图12(b)可以看出：各个数据参数都比较接近，不管是自变量系数、截距还是相关系数R2。但是从图12(c)和图12(d)可以看出：各个数据参数都存在比较大的差异；图12(c)拟合的比较好，每个数据几乎都在拟合线上，相关性比较大；图12(d)无论相较于图12(a)、图12(b)还是图12(c)，都有很大的差异。由此可以认为，决定这种差异的主要原因是细颗粒的质量分数。图12(a)和图12(b)模型的细颗粒质量分数都为70%，不同的只是粗颗粒某些粒径的质量分数不同。但是从图12(a)和图12(b)的拟合程度来看，两者之间存在高度的相似性。而图12(c)模型的细颗粒质量分数为60%，图12(d)模型的细颗粒质量分数为90%。从中可以看出：随着细颗粒质量分数的不断增大，模型的尺寸效应与抗剪强度的相关性就越小。

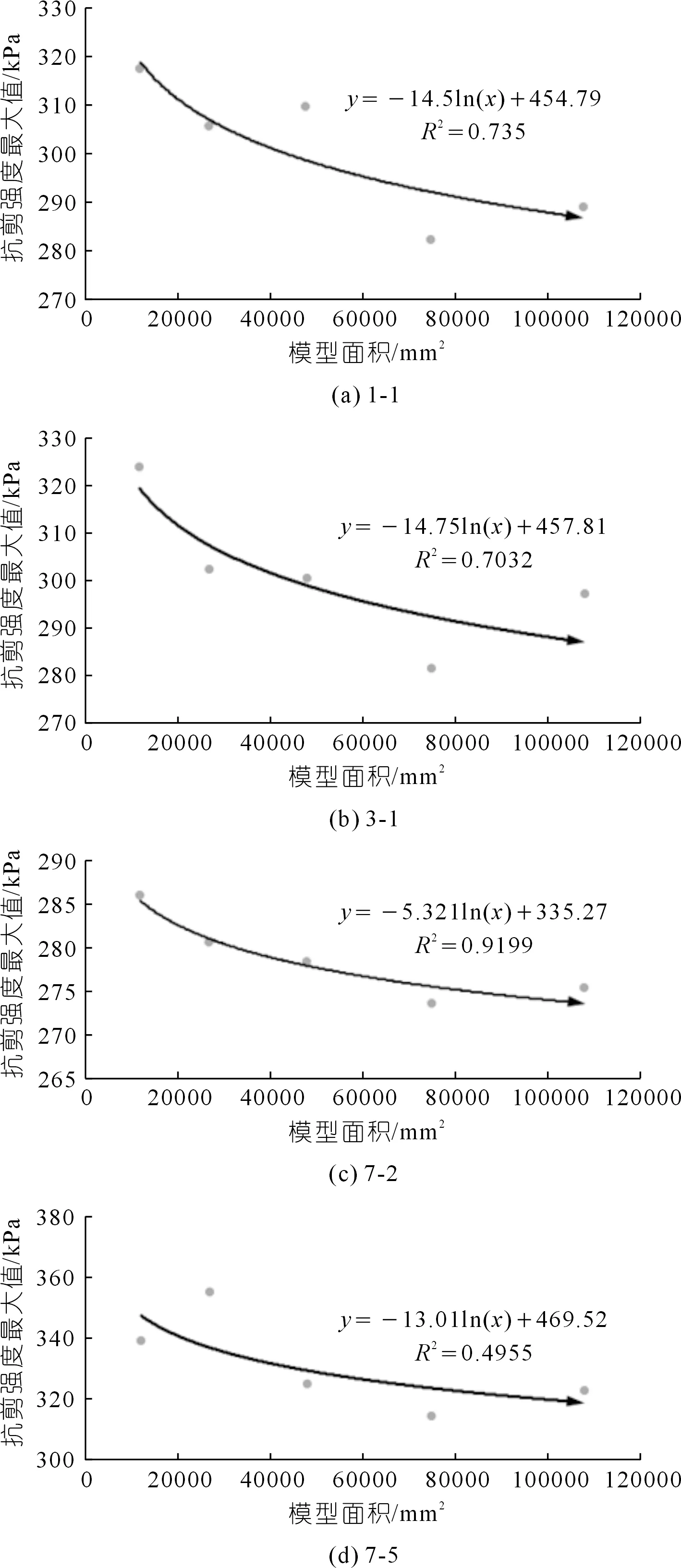
图12 抗剪强度与模型面积关系拟合Fig.12 Fitting relationship between shear strength and model area

4 结 论

(1) 通过研究不同颗粒级配组的颗粒含量对模型剪切强度产生的影响可以知道：① 在相同法向应力作用下，如果保持细颗粒的含量相同，只改变粗颗粒的含量，则土石混合体的剪切应力-剪切位移曲线不会发生较大的变动；② 但是如果细颗粒的含量发生改变，则细颗粒的含量越大，其对应的剪切应力就会越大；③ 细颗粒的含量越小，其对应的剪切应力就会越小。在土石混合体的抗剪强度中，细颗粒的含量多少对剪切应力的大小起到主要的影响。

(2) 通过对粒径含量的缺失对模型抗剪强度产生的影响可以知道：① 当细颗粒的含量≥85%时，剪切应力-剪切位移关系曲线发生比较大的波动；② 当细颗粒的含量<85%时，剪切应力-剪切位移关系曲线没有发生较大的波动。由此可以看出，细颗粒的粒径含量为85%，是区分剪切应力-剪切位移关系曲线是否波动的分界点。

(3) 通过对不同颗粒级配组的尺寸效应进行研究可以知道：模型的抗剪强度的大小总体来说随着尺寸面积的增大而不断减小。模型的尺寸效应与抗剪强度的相关性主要受细颗粒含量的影响。细颗粒含量越小，其对应的模型的尺寸效应与抗剪强度的相关性就会越强；反之，则其相关性就会越低。